- 1 Công văn 10803/BGDĐT-GDTrH hướng dẫn chương trình chuyên sâu môn chuyên cấp trung học phổ thông do Bộ Giáo dục và Đào tạo ban hành
- 2 Thông tư 56/2011/TT-BGDĐT về Quy chế thi chọn học sinh giỏi cấp quốc gia do Bộ trưởng Bộ Giáo dục và Đào tạo ban hành
- 3 Thông tư 41/2012/TT-BGDĐT sửa đổi Quy chế thi chọn học sinh giỏi cấp quốc gia kèm theo Thông tư 56/2011/TT-BGDĐT do Bộ trưởng Bộ Giáo dục và Đào tạo ban hành
- 4 Thông tư 37/2013/TT-BGDĐT sửa đổi Quy chế thi chọn học sinh giỏi cấp quốc gia kèm theo Thông tư 56/2011/TT-BGDĐT sửa đổi Thông tư 41/2012/TT-BGDĐT do Bộ trưởng Bộ Giáo dục và Đào tạo ban hành
| BỘ GIÁO DỤC VÀ ĐÀO TẠO | CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM |
| Số: 211/BGDĐT-QLCL | Hà Nội, ngày 16 tháng 01 năm 2023 |
| Kính gửi: | - Các Sở Giáo dục và Đào tạo; |
Kỳ thi chọn học sinh giỏi quốc gia trung học phổ thông (gọi tắt là Kỳ thi HSGQG) năm học 2022-2023 được thực hiện theo Quy chế thi chọn học sinh giỏi cấp quốc gia ban hành kèm theo Thông tư số 56/2011/TT-BGDĐT ngày 25/11/2011 và được sửa đổi bổ sung tại Thông tư số 41/2012/TT-BGDĐT ngày 19/11/2012; Thông tư số 37/2013/TT-BGDĐT ngày 27/11/2013; Thông tư số 02/2023/TT-BGDĐT ngày 06/01/2023 của Bộ trưởng Bộ Giáo dục và Đào tạo (gọi tắt là Quy chế thi). Để tổ chức tốt Kỳ thi, Bộ Giáo dục và Đào tạo (GDĐT) hướng dẫn các đơn vị dự thi một số nội dung sau:
a) Lịch thi:
- Tổ chức 02 buổi thi; không tổ chức thêm buổi thi thực hành đối với các môn Vật lí, Hóa học, Sinh học. Thời gian bắt đầu làm bài của mỗi buổi thi: 08 giờ 00.
Ngày 24/02/2023: Thi viết các môn Toán, Vật lí, Hóa học, Sinh học, Ngữ văn, Lịch sử, Địa lí, Tiếng Anh, Tiếng Nga, Tiếng Pháp, Tiếng Trung Quốc và thi lập trình trên máy vi tính môn Tin học.
Ngày 25/02/2023: Thi viết các môn Toán, Vật lí, Hóa học, Sinh học; thi nói các môn Tiếng Anh, Tiếng Nga, Tiếng Pháp, Tiếng Trung Quốc và thi lập trình trên máy vi tính môn Tin học.
- Thời gian làm bài thi của buổi thi viết và buổi thi môn Tin học là 180 phút; Thời gian làm bài của buổi thi nói các môn Ngoại ngữ thực hiện theo Phụ lục II kèm theo Công văn này.
b) Hình thức thi:
Môn Tin học thi theo hình thức lập trình trên máy vi tính; các môn khác thi theo hình thức thi viết, các môn ngoại ngữ có thêm hình thức thi nói (độc thoại).
Theo Chương trình giáo dục trung học phổ thông (THPT) hiện hành và Chương trình chuyên sâu các môn chuyên cấp THPT ban hành kèm theo Công văn số 10803/BGDĐT-GDTrH ngày 16/12/2009 của Bộ GDĐT.
Bộ GDĐT trực tiếp giao đề thi (chính thức và dự bị) cho Thủ trưởng đơn vị dự thi nơi đặt Hội đồng coi thi; địa điểm và thời gian giao nhận theo văn bản thông báo của Cục Quản lý chất lượng (QLCL). Trường hợp phải sử dụng đề thi dự bị, Bộ GDĐT sẽ quyết định và thông báo lịch thi; đồng thời, hướng dẫn việc sử dụng đề thi dự bị.
4. Số lượng thí sinh đăng ký dự thi
Số lượng thí sinh tối đa trong đội tuyển mỗi môn thi của từng đơn vị dự thi Kỳ thi HSGQG năm học 2022-2023 giữ ổn định theo số lượng thí sinh được đăng ký tối đa trong Kỳ thi HSGQG năm học 2021-2022.
5. Sử dụng công nghệ thông tin
Các đơn vị thống nhất sử dụng phần mềm quản lý thi HSG của Bộ GDĐT (gọi tắt là phần mềm thi HSG); phần mềm thi HSG và hướng dẫn sử dụng phần mềm thi HSG sẽ được Cục QLCL gửi về các đơn vị trước ngày 17/01/2023.
Phần mềm thi HSG cần được cài đặt trên máy vi tính hệ điều hành WINDOWS (phiên bản tối thiểu Windows 7) và phần mềm xử lý văn bản (phiên bản tối thiểu Office 2010).
Người chuyên trách sử dụng máy tính và phần mềm thi chọn học sinh giỏi phải am hiểu về công nghệ thông tin, sử dụng thành thạo phần mềm, có số điện thoại và địa chỉ email hoạt động thường xuyên.
Bản Đăng ký dự thi, Danh sách thí sinh và các báo cáo gửi về Cục QLCL phải được xuất từ phần mềm quản lý thi HSG.
- Mã số của các đơn vị dự thi trong Kỳ thi HSGQG tại Phụ lục I kèm theo Công văn này.
- Các đơn vị dự thi có trách nhiệm gửi về Cục QLCL:
Bản Đăng ký dự thi và file theo mẫu tại Phụ lục 1 trong phần mềm thi HSG, trước ngày 19/01/2023.
Bản Danh sách thí sinh đăng ký dự thi và file theo mẫu tại Phụ lục 2 trong phần mềm thi HSG, trước ngày 20/01/2023.
Các đơn vị dự thi thuộc cùng một Hội đồng coi thi ghép gửi thêm một bản Đăng ký dự thi và Danh sách thí sinh đăng ký dự thi và file về đơn vị dự thi nơi đặt Hội đồng coi thi ghép, trước ngày 18/01/2023.
7. Tổ chức các Hội đồng coi thi
Trước ngày 06/02/2023, Cục QLCL sẽ thông báo cho các đơn vị dự thi về việc tổ chức các Hội đồng coi thi và việc điều động nhân sự tham gia các Hội đồng coi thi.
Căn cứ văn bản điều động của Cục QLCL, các đơn vị cử nhân sự tham gia các Hội đồng coi thi đảm bảo đủ số lượng, đúng thành phần và đáp ứng đầy đủ các yêu cầu quy định tại khoản 2 Điều 11 của Quy chế thi. Danh sách nhân sự được cử tham gia Hội đồng coi thi phải được gửi đến Thủ trưởng đơn vị dự thi nơi đặt Hội đồng coi thi đó trước ngày 10/02/2023, để ra Quyết định thành lập Hội đồng coi thi.
Thủ trưởng của đơn vị dự thi nơi đặt Hội đồng coi thi chịu trách nhiệm tổ chức tiếp đón và bố trí nơi ăn, ở cho các cán bộ, chuyên viên, giảng viên, giáo viên từ các đơn vị dự thi khác đến tham gia Hội đồng coi thi.
Lưu ý: Người được cử đi coi thi môn Tin học và coi thi các môn Ngoại ngữ phải là giáo viên đang giảng dạy chính môn đó ở cấp THPT. Ngoài ra, giáo viên được cử đi coi các môn Ngoại ngữ phải biết sử dụng thành thạo máy vi tính và các thiết bị nghe nhìn.
8. Lịch làm việc của các Hội đồng coi thi
Các đơn vị dự thi và các Hội đồng coi thi cần lưu ý một số điểm dưới đây khi xây dựng kế hoạch triển khai công tác chuẩn bị và tổ chức coi thi:
* Ngày 23/02/2023:
- Các Hội đồng coi thi hoàn tất việc niêm yết tại mỗi phòng thi:
Quy định về trách nhiệm của thí sinh (Điều 27 Quy chế thi);
Quy định về các tài liệu và vật dụng thí sinh được phép mang vào phòng thi (Điều 26 Quy chế thi);
Danh sách thí sinh trong phòng thi.
- Tổ chức họp Hội đồng coi thi.
- Tập trung thí sinh để phổ biến Quy chế thi và các văn bản có liên quan tới Kỳ thi.
* Các ngày 24 và 25/02/2023:
- Trước 10 giờ 00 ngày 24 và 25/02/2023: Lãnh đạo các Hội đồng coi thi gửi email (hoặc báo cáo bằng điện thoại) về Cục QLCL để báo cáo nhanh số lượng thí sinh dự thi (tổng số và theo từng môn thi) và tình hình tổ chức coi thi. Các trường hợp đặc biệt (nếu có) phải được báo cáo ngay bằng điện thoại, kèm văn bản gửi qua email.
- Ngày 25/02/2023: Ngay sau khi kết thúc buổi thi, Chủ tịch Hội đồng coi thi chịu trách nhiệm gửi về Cục QLCL 01 (một) bưu kiện gồm 02 (hai) bì:
Một bì chứa túi số 4, quy định tại Điều 28 Quy chế thi;
Một bì đựng đĩa CD và Danh sách thí sinh dự thi theo Phụ lục 3.1 (bản in và file lưu trong đĩa CD, xuất từ phần mềm quản lý thi HSG của đơn vị sau khi đã cập nhật thông tin sau buổi thi cuối của Kỳ thi, có xác nhận của Chủ tịch Hội đồng coi thi).
Bưu kiện được gửi qua hệ thống chuyển phát của Tổng Công ty Bưu điện Việt Nam; thông tin người nhận sẽ được Cục QLCL thông báo tới các đơn vị trước ngày 20/02/2023.
- Trước 15 giờ 30 ngày 25/02/2023: Cập nhật thí sinh vắng thi vào phần mềm quản lý thi HSG; sau đó, xuất từ phần mềm ra dữ liệu file gốc (*.DBF), file Phụ lục 3.1 (file excel), file Phụ lục 3.2 (file excel); tổng hợp báo cáo công tác coi thi của đơn vị (file scan, file word); gửi tất cả các file trên qua email: hsgqg@moet.gov.vn.
a) Chuẩn bị và tổ chức coi thi buổi thi nói của các môn Ngoại ngữ: Công tác chuẩn bị, thực hiện theo Phụ lục II đính kèm Công văn này.
b) Chuẩn bị và tổ chức coi thi môn Tin học:
- Đối với việc chuẩn bị và tổ chức coi thi môn Tin học: Cùng với việc thực hiện Quy chế thi, cần lưu ý thực hiện các điểm dưới đây:
- Cài đặt phần mềm cho các máy vi tính:
Hệ điều hành: Microsoft Windows hoặc Linux;
Môi trường lập trình: Free Pascal/Lazarus, Code Block/Dev-C và các môi trường tương đương khác (riêng kỳ thi chọn đội tuyển Olympic không sử dụng Free Pascal/Lazarus);
Phần mềm ghi đĩa CD.
Cần đặt ngày giờ chính xác cho hệ thống; quét sạch virus cho các máy vi tính; không được cài đặt phần mềm và các tài liệu khác. Việc cài đặt phải được hoàn thành trước ngày 23/02/2023.
- Chuẩn bị đĩa CD (có đĩa CD dự phòng) để ghi bài làm của thí sinh: Thống nhất dùng loại đĩa Maxell, đĩa mới trong hộp còn nguyên bao bì.
- Chuẩn bị đủ giấy thi để in bài làm của thí sinh; chuẩn bị mực in dự phòng, bàn dập ghim kèm theo hộp ghim, bút chuyên dùng ghi trên đĩa CD (TWIN CD MARKER).
- Trong quá trình coi thi, giám thị cần lưu ý một số điểm sau:
Quản lý đĩa CD như quản lý giấy thi; chỉ phát cho thí sinh đĩa CD mới, đựng trong hộp còn nguyên bao bì.
Niêm phong các đĩa CD ghi file bài làm của thí sinh và các bài làm in trên giấy của mỗi phòng thi, riêng theo từng loại.
- Một số điểm lưu ý đối với thí sinh dự thi:
Ghi rõ các thông tin (kể cả số tờ giấy đã dùng để in bài làm) vào phần phách ở tờ giấy thứ nhất dùng để in bài làm; đối với các tờ giấy sau, chỉ ghi số báo danh dự thi. Ngoài các thông tin vừa nêu, không ghi bất kì dấu hiệu nào khác lên tờ giấy in bài làm.
Ghi số báo danh, ngày thi và ký tên lên đĩa CD ghi file bài làm.
c) Các đơn vị cần quán triệt cho học sinh dự thi môn Toán: Danh mục các khái niệm, kết quả thí sinh môn Toán được phép sử dụng như khái niệm, kết quả sách giáo khoa trong Kỳ thi chọn HSG cấp quốc gia, được quy định tại các Công văn số 11636/THPT ngày 25/12/2000 và 1403/THPT ngày 25/02/2002 của Bộ GDĐT (Phụ lục III đính kèm).
d) Nếu đến ngày 10/02/2023 chưa nhận được giấy thi, túi đựng bài thi, đơn vị dự thi nơi đặt Hội đồng coi thi phải liên hệ ngay với Cục QLCL để xử lý kịp thời.
đ) Chuẩn bị nguồn điện: Đơn vị dự thi nơi đặt Hội đồng coi thi phải chuẩn bị nguồn điện dự phòng có đủ công suất và điện áp để Hội đồng coi thi sử dụng.
e) Người liên hệ về công tác tổ chức thi của đơn vị dự thi và người phụ trách công nghệ thông tin phục vụ tổ chức thi tại đơn vị dự thi phải là cán bộ, chuyên viên thuộc sở GDĐT hoặc đại học, trường đại học, có số điện thoại và hộp thư điện tử hoạt động thường xuyên.
g) Khi gửi các dữ liệu file, thông tin của Kỳ thi HSGQG về Cục QLCL theo đường email, các đơn vị gửi theo địa chỉ: hsgqg@moet.gov.vn. Các đơn vị dự thi cần thường xuyên vào hộp thư điện tử đã đăng ký để cập nhật và xử lý thông tin liên quan đến Kỳ thi.
h) Hết giờ làm bài thi, các giám thị chỉ cho thí sinh rời khỏi phòng thi sau khi hoàn tất việc thu bài thi của tất cả thí sinh.
Nhận được Công văn này, các đơn vị nghiên cứu và nghiêm túc triển khai thực hiện. Trường hợp cần trao đổi thêm về các vấn đề liên quan tới Kỳ thi, các đơn vị liên hệ với Cục Quản lý chất lượng, 35 Đại Cồ Việt, Quận Hai Bà Trưng, Hà Nội, theo địa chỉ e-mail: hsgqg@moet.gov.vn; điện thoại: (024)38683992, (024)36231655./.
|
| TL. BỘ TRƯỞNG |
QUY ĐỊNH MÃ SỐ CÁC ĐƠN VỊ DỰ THI KỲ THI CHỌN HỌC SINH GIỎI QUỐC GIA THPT NĂM HỌC 2022-2023
(Kèm theo Công văn số 211/BGDĐT-QLCL ngày 16 tháng 01 năm 2023)
| Mã số đơn vị | Tên đơn vị | Mã số đơn vị | Tên đơn vị |
| 01 | An Giang | 37 | Lào Cai |
| 02 | Bà Rịa -Vũng Tàu | 38 | Long An |
| 03 | Bắc Giang | 39 | Nam Định |
| 04 | Bắc Kạn | 40 | Nghệ An |
| 05 | Bạc Liêu | 41 | Ninh Bình |
| 06 | Bắc Ninh | 42 | Ninh Thuận |
| 07 | Bến Tre | 43 | Phú Thọ |
| 08 | Bình Định | 44 | Phú Yên |
| 09 | Bình Dương | 45 | Quảng Bình |
| 10 | Bình Phước | 46 | Quảng Nam |
| 11 | Bình Thuận | 47 | Quảng Ngãi |
| 12 | Cà Mau | 48 | Quảng Ninh |
| 13 | Cần Thơ | 49 | Quảng Trị |
| 14 | Cao Bằng | 50 | Sóc Trăng |
| 15 | Đà Nẵng | 51 | Sơn La |
| 16 | Đắk Lắk | 52 | Tây Ninh |
| 17 | Đắk Nông | 53 | Thái Bình |
| 18 | Điện Biên | 54 | Thái Nguyên |
| 19 | Đồng Nai | 55 | Thanh Hoá |
| 20 | Đồng Tháp | 56 | Thừa Thiên - Huế |
| 21 | Gia Lai | 57 | Tiền Giang |
| 22 | Hà Giang | 58 | TP. Hồ Chí Minh |
| 23 | Hà Nam | 59 | Trà Vinh |
| 24 | Hà Nội | 60 | Tuyên Quang |
| 25 | Hà Tĩnh | 61 | Vĩnh Long |
| 26 | Hải Dương | 62 | Vĩnh Phúc |
| 27 | Hải Phòng | 63 | Yên Bái |
| 28 | Hậu Giang | 65 | Đại học Quốc gia Hà Nội |
| 29 | Hoà Bình | 66 | Đại học Quốc gia TP. Hồ Chí Minh |
| 30 | Hưng Yên | 67 | Trường ĐHSP Hà Nội |
| 31 | Khánh Hoà | 68 | Trường Đại học Vinh |
| 32 | Kiên Giang | 69 | Trường PT Vùng cao Việt Bắc |
| 33 | Kon Tum | 70 | Trường ĐHSP TP. Hồ Chí Minh |
| 34 | Lai Châu | 71 | Đại học Huế |
| 35 | Lâm Đồng | 72 | Trường Đại học Tân Tạo |
| 36 | Lạng Sơn |
|
|
QUY ĐỊNH
VỀ CÔNG TÁC CHUẨN BỊ TỔ CHỨC THI NÓI CÁC MÔN NGOẠI NGỮ KỲ THI CHỌN HỌC SINH GIỎI QUỐC GIA NĂM HỌC 2022-2023
(Kèm theo Công văn số 211/BGDĐT-QLCL ngày 16 tháng 01 năm 2023)
I. Công tác chuẩn bị và tổ chức thi của thí sinh
1. Tổ chức thi thử bài thi nói
| STT | Nội dung | Thời gian |
| 1 | Cục QLCL gửi đường link download phần mềm tới các đơn vị qua email | Trước ngày 21/02/2023 |
| 2 | Các đơn vị tiến hành cài đặt phần mềm tổ chức thi nói | Trước ngày 22/02/2023 |
| 3 | Tổ chức cho thí sinh thi thử bài thi nói các môn ngoại ngữ (từ 08h00 đến 16h00). Lưu ý: các đơn vị tự chuẩn bị đề thi nói để thí sinh thi thử hoặc cho thí sinh giới thiệu về bản thân | Trong ngày 23/02/2023 |
2. Tổ chức thi chính thức bài thi nói
| STT | Nội dung | Thời gian |
| 1 | Cục QLCL gửi đường link download file cấu hình hệ thống để chuẩn bị cho buổi thi chính thức qua email (ngay sau khi kết thúc buổi thi thử) | Trong ngày 23/02/2023 |
| 2 | Cục QLCL gửi đường link download tới các đơn vị tiến hành cập nhật file cấu hình hệ thống vào các máy tính dùng để tổ chức thi chính thức và quy trình sử dụng phần mềm thi nói khi không có Internet và có mạng Internet | Trước ngày 24/02/2023 |
| 3 | Tổ chức buổi thi chính thức cho các thí sinh | Theo lịch thi chung |
3. Thời gian làm bài thi của thí sinh:
Thời gian làm bài thi nói của mỗi thí sinh là 10 phút; trong đó 05 phút chuẩn bị, 05 phút tiếp theo trả lời và ghi âm.
II. Chuẩn bị cơ sở vật chất
1. Bố trí phòng thi
a) Tại mỗi Hội đồng coi thi phải có:
- Ít nhất một phòng thi riêng cho mỗi môn Ngoại ngữ có thí sinh dự thi;
- Có 02 phòng chờ chung cho tất cả các môn Ngoại ngữ có thí sinh dự thi; phòng chờ một để thí sinh ngồi chờ trước khi vào phòng thi, phòng chờ hai để thí sinh ngồi nghỉ sau khi đã hoàn thành phần thi của mình.
b) Các phòng chờ và các phòng thi nói phải được bố trí đảm bảo thuận lợi cho việc đi lại của thí sinh giữa phòng chờ và phòng thi.
c) Các phòng chờ và phòng thi nói phải được bố trí tại một khu tách biệt với các phòng thi khác, đảm bảo việc thi nói các môn Ngoại ngữ không gây ảnh hưởng tới việc làm bài thi của thí sinh dự thi các môn khác.
2. Chuẩn bị thiết bị và văn phòng phẩm
a) Loại thiết bị và văn phòng phẩm:
- Máy vi tính (có bàn phím và chuột kèm theo) đáp ứng các thông số kỹ thuật tối thiểu sau đây:
CPU: Intel Pentium 4.3GHz;
RAM: 2GB;
Hard disk: 40GB;
NIC: 10/100mbps;
Có ổ ghi đĩa CD hoặc DVD Rewrite hoạt động tốt;
Monitor: 14”, độ phân giải tối thiểu: 1024x768, độ sâu màu: 65K;
Card sound: Creative Sound Blaster Live hoặc loại tương thích với phần mềm;
OS: Windows 7 32 bit.
- Headphone (kèm mic) Voiceao 5200MV đáp ứng các thông số kỹ thuật sau đây:
|
| Phone | Mic |
| Dimension | 40mm | 6x5mm |
| Frequency Range | 20-20,000Hz | 30-16000Hz |
| Sensitivity | 103dB S.P.L at 1KHz | -58dB±3dB |
| Impedance | 32Ω |
|
| Rated power | 15mW |
|
| Power Capability | 150mV | 3V |
- Một số lưu ý bắt buộc với máy tính sử dụng để thi nói:
Hệ điều hành từ Win 7 trở lên (yêu cầu cài đúng bản của Microsoft, không dùng các bản mod, hoặc không đúng bản chuẩn);
Cài đặt Microsoft Dot Net framwork 4.5 trở lên;
Cài đặt chương trình giải nén VD: 7 zip.
Phần mềm tổ chức thi nói đã tích hợp chức năng ghi đĩa CD/DVD nên máy tính không cần cài đặt phần mềm ghi đĩa CD/DVD, tránh xung đột. Cần kiểm tra đầu đĩa trước khi thi, tránh tình trạng không ghi được đĩa CD/DVD.
- Đĩa CD/DVD: Đĩa Maxell mới, đựng trong hộp còn nguyên bao bì.
- Giấy nháp.
b) Số lượng:
- Đảm bảo mỗi phòng thi được bố trí:
Hai (02) máy vi tính, gồm một máy dành cho thí sinh sử dụng và một máy dự phòng;
Hai bộ Headphone (kèm mic) Voiceao 5200MV, gồm một bộ để thí sinh sử dụng và một bộ dự phòng.
- Đảm bảo mỗi thí sinh có một (01) đĩa CD/DVD riêng để ghi file ghi âm phần trả lời (gọi tắt là file ghi âm) của mình.
c) Chuẩn bị kỹ thuật:
- Trong mỗi phòng thi, 02 máy vi tính được kết nối internet; đảm bảo việc kết nối với máy chủ của Bộ GDĐT được liên tục trong suốt thời gian thi. Máy vi tính có ổ ghi đĩa CD/DVD.
- Cài đặt cho mỗi máy vi tính các phần mềm: Trình duyệt firefox 46 trở lên, Chrome 50 trở lên, Flash player, Windows Media firefox plugin và phần mềm ghi đĩa CD/DVD; phần mềm tổ chức thi nói do Bộ GDĐT cung cấp.
Việc cài đặt do các cán bộ công nghệ thông tin của Hội đồng coi thi thực hiện và phải được hoàn tất trước ngày thi ít nhất 01 ngày.
3. Bố trí giám thị
a) Đối với mỗi phòng thi, bố trí ba (03) giám thị, gồm hai (02) giám thị trong phòng thi và một (01) giám thị ngoài phòng thi;
b) Đối với mỗi phòng chờ, bố trí hai (02) giám thị, gồm một (01) giám thị trong phòng chờ và một (01) giám thị ngoài phòng chờ.
4. Công việc của giám thị
a) Trước giờ thi:
- Giám thị trong phòng thi kiểm tra Thẻ dự thi của thí sinh (TS) trước khi cho TS vào phòng thi;
- Tập trung TS của tất cả các môn thi Ngoại ngữ trong phòng chờ 1;
- Tại mỗi phòng thi, giám thị trong phòng thi kiểm tra việc kết nối mạng Internet của các máy vi tính (kể cả máy vi tính dự phòng);
- Kiểm tra, điều chỉnh ngày, giờ trên hệ thống của các máy vi tính chính xác;
- Nhận giấy nháp, đĩa CD/DVD, đề thi từ Chủ tịch Hội đồng coi thi rồi chuyển về phòng thi;
- Ký tên vào giấy nháp (cả hai giám thị trong phòng thi cùng ký);
- Yêu cầu TS chỉ được phép mang bút viết vào phòng thi; lần lượt cho các TS thực hiện phần thi của mình theo đúng thứ tự trong Danh sách TS của phòng thi.
b) Khi có hiệu lệnh, giám thị trong phòng thi cho TS thứ nhất trong Danh sách TS của phòng thi vào phòng thi. Sau khi TS thi xong, giám thị trong phòng thi yêu cầu TS ký xác nhận vào Phiếu thu bài thi (kể cả trường hợp TS không nói gì để ghi âm); cho TS ra khỏi phòng thi và gọi TS tiếp theo vào phòng thi.
c) Trong thời gian thi, giám thị ngoài phòng thi có trách nhiệm giám sát TS và giám thị trong phòng thi; giám sát việc di chuyển của TS từ phòng chờ 1 đến phòng thi và từ phòng thi đến phòng chờ 2, đảm bảo TS không tiếp xúc với bất kỳ ai khác.
d) Giám thị trong phòng chờ điều hành hoạt động của TS trong phòng chờ để đảm bảo giữ trật tự.
đ) Giám thị ngoài phòng chờ có trách nhiệm giám sát TS và giám thị trong phòng chờ; giám sát việc TS ra ngoài phòng chờ.
5. Một số lưu ý:
a) Khi hệ thống bắt đầu ghi âm, TS phải đọc mã số của đề thi, nội dung của câu hỏi trong đề thi trước khi bắt đầu trả lời bằng ngôn ngữ dự thi. Thí sinh không đọc họ tên, số báo danh (nếu vi phạm quy định này, bài thi nói của TS sẽ bị coi là phạm quy).
b) Khi ghi âm bài thi, TS phải nói to, rõ ràng.
c) TS không được đề cập đến các thông tin cá nhân trong phần trả lời, không được tạo ra các tiếng động nhằm đánh dấu phần thi của mình.
d) Giám thị trong phòng thi không được tạo ra tiếng động lạ khi hệ thống đang ghi âm phần trả lời của TS.
đ) Trong thời gian tổ chức thi nói, nếu xảy ra các sự cố mất điện, mất kết nối mạng Internet, các Hội đồng coi thi cần bình tĩnh xử lý theo hướng dẫn của Cục QLCL./.
DANH MỤC KHÁI NIỆM, KẾT QUẢ THÍ SINH MÔN TOÁN ĐƯỢC PHÉP SỬ DỤNG NHƯ KHÁI NIỆM, KẾT QUẢ SÁCH GIÁO KHOA KỲ THI CHỌN HỌC SINH GIỎI QUỐC GIA THPT NĂM HỌC 2022-2023
(Kèm theo Công văn số 211/BGDĐT-QLCL ngày 16 tháng 01 năm 2023)
Ngoài các kiến thức toán theo Chương trình phổ thông (từ lớp 1 đến lớp 12) hiện hành, các học sinh dự thi ở môn Toán trong kỳ thi chọn học sinh giỏi quốc gia THPT được phép sử dụng các khái niệm và kết quả dưới đây như khái niệm và kết quả sách giáo khoa:
I. Phần Số học:
- Các khái niệm và kết quả lý thuyết được trình bày trong Chương I; §1, §2, §4 Chương II; §1, §2, §3 Chương III; Chương IV và Chương V cuốn "Bài giảng số học" của nhóm Tác giả: Đặng Hùng Thắng (Chủ biên), Nguyễn Văn Ngọc, Vũ Kim Thủy (NXB Giáo dục, 1994).
- Định lý nhỏ Phécma, Định lý Uynsơn.
- Định lí Ơle và định lí Trung Quốc về các số dư.
II. Phần Đại số - Giải tích:
1. Bất đẳng thức (Bđt):
- Các bất đẳng thức đại số: Bđt Côsi cho n (n ϵ Z, n ≥ 2) số thực không âm; Bđt Bunhiacôpxki cho hai bộ n số thực (n ϵ Z, n ≥ 2); Bđt Trêbưsep cho hai dãy n số thực (n ϵ Z, n ≥ 2); Bđt Nesbit cho ba số thực dương; Bđt Becnuli mở rộng.
- Bất đẳng thức hàm lồi (Bất đẳng thức Jensen).
- Các bất đẳng thức tích phân được trình bày trong mục 3 của §2 Chương III SGK Giải tích 12 (Sách chỉnh lí hợp nhất năm 2000, NXB Giáo dục).
- Kết quả của Ví dụ 1.4 trong §1 Chương V cuốn "Bất đẳng thức" của Tác giả Phan Đức Chính (NXB Giáo dục, 1993).
2. Đa thức:
- Khái niệm nghiệm bội của đa thức và một số kết quả đơn giản liên quan đến nghiệm của một đa thức:
# Định lí 1. Đa thức bậc n (n ϵ N*) có tối đa n nghiệm thực, mỗi nghiệm được kể số lần bằng số bội của nó.
# Định lí 2. Nếu x0 là nghiệm của đa thức P(x) thì x0 a là nghiệm của đa thức P(x - a), với a ϵ R cho trước.
# Định lí 3. Nếu x0 ≠ 0 là nghiệm của đa thức:
P(x) = a0xn a1xn-1 ... an-1x an , a0 ≠ 0 và n ϵ N*,
thì 1/x0 là nghiệm của đa thức:
Q(x) = anxn an-1xn-1 ... a1x a0.
# Định lí 4. Nếu x0 là nghiệm bội k (k ϵ Z, k ≥ 2) của đa thức P(x) thì x0 là nghiệm bội k - 1 của đa thức đạo hàm P/(x).
# Định lí 5. Nếu x0 là nghiệm hữu tỉ của đa thức với hệ số nguyên:
P(x) = a0xn a1xn-1 ... an-1x an , a0 ≠ 0 và n ϵ N*,
thì x0 phải có dạng p/q; trong đó p, q tương ứng là ước của an, a0.
# Định lí Viet thuận và đảo cho đa thức bậc n (n ϵ Z, n ≥ 2).
- Công thức nội suy Lagrange.
- Khái niệm đa thức khả quy, bất khả quy.
- Định lí Bơdu về số dư trong phép chia một đa thức cho nhị thức bậc nhất x - a.
- Đa thức Trêbưsep và các tính chất được trình bày trong phần 1 Phụ lục 3 cuốn "Bất đẳng thức" của Tác giả Phan Đức Chính (NXB Giáo dục, 1993).
3. Dãy số - Hàm số:
- Phương trình đặc trưng và công thức tính số hạng tổng quát của dãy số được cho bởi hệ thức truy hồi tuyến tính.
- Các khái niệm: dãy con, dãy số tuần hoàn và chu kỳ của dãy số tuần hoàn.
- Mối liên hệ giữa tính hội tụ của một dãy số và tính hội tụ của các dãy con của dãy số đó.
- Một số kết quả đơn giản về tính đơn điệu của hàm số:
# Kết quả 1: Nếu f và g là các hàm số đồng biến (nghịch biến) trên tập X thì f g cũng là hàm số đồng biến (nghịch biến) trên tập X.
# Kết quả 2: Giả sử f và g là các hàm số đồng biến (nghịch biến) trên tập X. Khi đó:
i) Nếu f và g chỉ nhận giá trị không âm (không dương) trên X thì f.g sẽ là hàm số đồng biến trên tập X.
ii) Nếu f và g chỉ nhận giá trị không dương (không âm) trên X thì f.g sẽ là hàm số nghịch biến trên tập X.
# Kết quả 3: Giả sử f là hàm số đồng biến và g là hàm số nghịch biến trên tập X. Khi đó, nếu f chỉ nhận giá trị không âm (không dương) trên X và đồng thời g chỉ nhận giá trị không dương (không âm) trên tập đó thì f.g sẽ là hàm số nghịch biến (đồng biến) trên X.
# Kết quả 4: Giả sử g là hàm số đồng biến (nghịch biến) trên tập X. Kí hiệu g(X) là tập giá trị của hàm g với tập xác định X. Khi đó:
i) Nếu f là hàm số đồng biến trên g(X) thì f(g(x)) sẽ là hàm số đồng biến (nghịch biến) trên X.
ii) Nếu f là hàm số nghịch biến trên g(X) thì f(g(x)) sẽ là hàm số nghịch biến (đồng biến) trên X.
# Kết quả 5: Nếu f là hàm số đồng biến trên R thì hai phương trình sau sẽ tương đương với nhau:
f(f(… (f(x))…)) = x và f(x) = x
- Khái niệm chu kỳ cơ sở của hàm số tuần hoàn và một số kết quả liên quan đến hàm tuần hoàn:
# Định lí 6. Nếu hàm số f(x) tuần hoàn trên tập X với chu kỳ cơ sở T và nếu:
f(x) - f(x A) ![]()
thì phải có A = kT, với k ϵ Z.
# Định lí 7. Nếu hàm số tuần hoàn f(x) có chu kỳ cơ sở T thì hàm số f(ax) (a ≠ 0) là hàm số tuần hoàn và có chu kỳ cơ sở T/a.
# Định lí 8. Nếu các hàm số f1(x) , f2(x) tuần hoàn trên X và tương ứng có các chu kỳ T1, T2 thông ước với nhau thì các hàm số f1(x) f2(x), f1(x) - f2(x), f1(x)f2(x) cũng tuần hoàn trên X.
- Định nghĩa hàm số ngược.
- Định nghĩa các hàm số lượng giác ngược arcsinx, arccosx arctgx, arccotgx và các hàm đạo hàm của chúng.
- Định lý về giá trị trung gian của hàm số liên tục trên một đoạn.
- Kết quả các Bài toán 1-7 trong §1 Chương II cuốn "Phương trình hàm" của Tác giả Nguyễn Văn Mậu (NXB Giáo dục, 1997).
III. Phần Lượng giác:
- Hệ thức Salơ cho các cung lượng giác.
- Bất phương trình lượng giác và tập nghiệm của các bất phương trình lượng giác cơ bản.
- Các công thức đơn giản tính độ dài đường phân giác, bán kính đường tròn nội tiếp, bán kính đường tròn bàng tiếp của một tam giác theo độ dài các cạnh và giá trị lượng giác của các góc của tam giác ấy.
- Một số bất đẳng thức thông dụng trong tam giác:
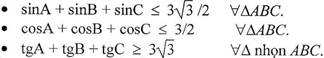
Dấu "=" trong các bất đẳng thức trên xảy ra khi và chỉ khi ΔABC là tam giác đều.
IV. Phần Hình học:
1. Hình học phẳng:
- Khái niệm trọng tâm, tâm tỉ cự của một hệ điểm và toạ độ của chúng xét trong hệ toạ độ Đêcac.
- Tâm đẳng phương của ba đường tròn.
- Hàng điểm điều hoà và Chùm điều hoà: Định nghĩa và một số tính chất đơn giản:
# Hệ thức Niutơn, Hệ thức Đêcac.
# Định lí 9. Hai cạnh của một tam giác cùng các đường phân giác trong, ngoài xuất phát từ đỉnh chung của hai cạnh ấy lập thành một chùm điều hoà.
- Định lí Ptôlêmê, Định lí Xêva, Định lí Mênêlaut, Định lí Thales thuận và đảo.
- Định nghĩa đường tròn Apoloniut, đường tròn Ơle (đường tròn 9 điểm).
- Kết quả của các Ví dụ 1, 2 trong phần 4 §4 Chương II SGK Hình học 10 (Sách chỉnh lí hợp nhất năm 2000, NXB Giáo dục).
- Hệ thức Ơle trong tam giác:
d2 = R2- 2Rr
trong đó: d, R, r tương ứng là khoảng cách giữa tâm đường tròn ngoại tiếp và tâm đường tròn nội tiếp, bán kính đường tròn ngoại tiếp, bán kính đường tròn nội tiếp của một tam giác.
- Định nghĩa tích các phép biến hình và một số kết quả liên quan, định nghĩa và các tính chất của phép đồng dạng: như đã được trình bày trong TLGKTĐ Hình học lớp 11 Ban KHTN-THCB (NXB Giáo dục, 1997).
- Các kết quả lí thuyết liên quan tới các phép biến hình trong mặt phẳng được trình bày trong cuốn "Các bài toán về hình học phẳng" (T.1 và T.2) của Tác giả Praxolov V.V. (NXB Hải Phòng, 1994).
- Định nghĩa và các tính chất của phép nghịch đảo được trình bày trong phần "Các kiến thức cơ bản" Chương 28 cuốn "Các bài toán về hình học phẳng" T.2 của Tác giả V.V. Praxolov (NXB Hải Phòng, 1994).
2. Hình học không gian:
- Định lí Thales thuận và đảo.
- Định nghĩa khối đa diện đều, khối tứ diện gần đều, khối tứ diện trực tâm và một số kết quả liên quan:
# Định lí 10. Tứ diện ABCD là tứ diện gần đều khi và chỉ khi xảy ra ít nhất một trong các điều sau:
i) Các mặt của tứ diện có diện tích bằng nhau.
ii) Bốn đường cao của tứ diện có độ dài bằng nhau.
iii) Có ít nhất hai trong ba điểm sau trùng nhau: tâm mặt cầu nội tiếp, tâm mặt cầu ngoại tiếp và trọng tâm của tứ diện.
# Định lí 11. Tứ diện ABCD là tứ diện trực tâm khi và chỉ khi xảy ra ít nhất một trong các điều sau:
i) Các cặp cạnh đối của tứ diện vuông góc với nhau.
ii) Chân đường vuông góc hạ từ một đỉnh xuống mặt đối diện là trực tâm của mặt ấy.
iii) Tổng bình phương độ dài của các cặp cạnh đối bằng nhau.
- Định lí về sự tồn tại của mặt cầu ngoại tiếp khối đa diện.
- Kết quả của Ví dụ 1 trong §1 Chương II SGK Hình học 12 (Sách chỉnh lí hợp nhất năm 2000, NXB Giáo dục).
- Khái niệm trọng tâm, tâm tỉ cự của một hệ điểm và toạ độ của chúng xét trong hệ toạ độ Đêcac.
- Định nghĩa và tính chất của tích có hướng của hai vectơ, tích hỗn tạp của ba vectơ cùng một số kết quả liên quan: như đã được trình bày trong §3 và §8 Chương II SGK Hình học 12 (Sách chỉnh lí hợp nhất năm 2000, NXB Giáo dục).
V. Phần Tổ hợp:
- Nguyên lí Dirichlet, Nguyên lí cực hạn (hay Nguyên lí khởi đầu cực trị).
- Định nghĩa ánh xạ, đơn ánh, toàn ánh, song ánh, ánh xạ tích.
- Các khái niệm và kết quả được trình bày trong §1, §2 và §3 của tài liệu "về một số vấn đề của giải tích tổ hợp trong chương trình THPT" (Biên soạn: Nguyễn Khắc Minh. Tài liệu báo cáo tại Hội nghị tập huấn giáo viên giảng dạy chuyên toán toàn quốc, Hà Nội-1997).
- Kết quả của các Bài toán 1, 4, 5 trong §4 của bài viết nói trên.
- Các khái niệm cơ bản của Lí thuyết đồ thị: Đồ thị; đỉnh, đỉnh cô lập, cạnh vô hướng, cạnh có hướng của đồ thị; đồ thị có hướng; đồ thị đơn vô hướng hữu hạn; đồ thị đầy đủ; đồ thị bù; đồ thị con; bậc của đỉnh trong đồ thị đơn vô hướng hữu hạn; đồ thị thuần nhất; đường đi, độ dài đường đi, đường đi khép kín, xích (có tài liệu gọi là đường đi đơn giản), xích đơn, chu trình (có tài liệu gọi là chu trình đơn giản), chu trình đơn, đường đi Ơle, đường đi Hamintơn, chu trình Ơle, chu trình Hamintơn trong đồ thị đơn vô hướng hữu hạn; đồ thị liên thông, đồ thị Ơle, đồ thị Hamintơn, cây, đồ thị lưỡng phân (có tài liệu gọi là đồ thị hai phe); thành phần liên thông của đồ thị đơn vô hướng hữu hạn.
- Một số kết quả đơn giản của Lí thuyết đồ thị:
# Định lí 12. Số đỉnh bậc lẻ trong một đồ thị đơn vô hướng hữu hạn là một số chẵn.
# Định lí 13. Trong đồ thị đơn vô hướng n đỉnh (n ϵ Z, n ≥ 2) tồn tại ít nhất hai đỉnh có cùng bậc.
# Định lí 14. Nếu đồ thị G đơn vô hướng n đỉnh (n ϵ Z, n ≥ 2) có đúng hai đỉnh cùng bậc thì G phải có đúng một đỉnh bậc 0 hoặc đúng một đỉnh bậc n - 1.
# Định lí 15. Mỗi đồ thị đơn vô hướng hữu hạn không liên thông đều bị phân chia một cách duy nhất thành các thành phần liên thông.
# Định lí 16. Nếu mỗi đỉnh của đồ thị G đơn vô hướng n đỉnh (n ϵ Z, n ≥ 2) đều có bậc không nhỏ hơn n/2 thì G là đồ thị liên thông.
# Định lí 17. Đồ thị G đơn vô hướng hữu hạn là đồ thị Ơle khi và chỉ khi hai điều kiện sau được đồng thời thoả mãn:
i) G là đồ thị liên thông.
ii) Mọi đỉnh của G đều có bậc chẵn.
# Định lí 18 Nếu tất cả các cạnh của một đồ thị đơn vô hướng đầy đủ 6 đỉnh được tô bởi hai màu thì phải tồn tại ít nhất một chu trình đơn độ dài 3 có tất cả các cạnh cùng màu.
- Khái niệm "chiến lược thắng cuộc" trong các bài toán trò chơi./.
- 1 Công văn 10803/BGDĐT-GDTrH hướng dẫn chương trình chuyên sâu môn chuyên cấp trung học phổ thông do Bộ Giáo dục và Đào tạo ban hành
- 2 Thông tư 56/2011/TT-BGDĐT về Quy chế thi chọn học sinh giỏi cấp quốc gia do Bộ trưởng Bộ Giáo dục và Đào tạo ban hành
- 3 Thông tư 41/2012/TT-BGDĐT sửa đổi Quy chế thi chọn học sinh giỏi cấp quốc gia kèm theo Thông tư 56/2011/TT-BGDĐT do Bộ trưởng Bộ Giáo dục và Đào tạo ban hành
- 4 Thông tư 37/2013/TT-BGDĐT sửa đổi Quy chế thi chọn học sinh giỏi cấp quốc gia kèm theo Thông tư 56/2011/TT-BGDĐT sửa đổi Thông tư 41/2012/TT-BGDĐT do Bộ trưởng Bộ Giáo dục và Đào tạo ban hành

