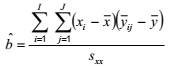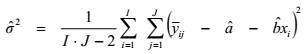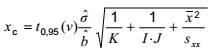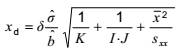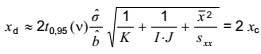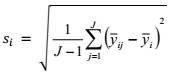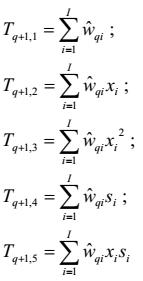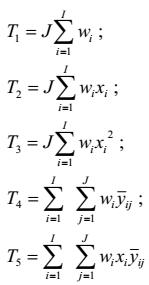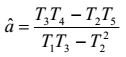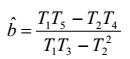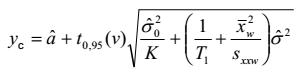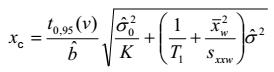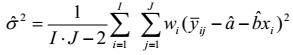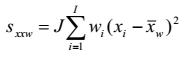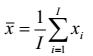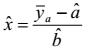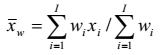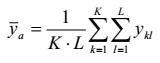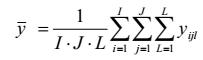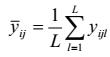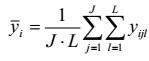NĂNG LỰC PHÁT HIỆN - PHẦN 2: PHƯƠNG PHÁP LUẬN TRONG TRƯỜNG HỢP HIỆU CHUẨN TUYẾN TÍNH
Capability of detection - Part 2: Methodology in the linear calibration case
Lời nói đầu
TCVN 10431-2:2014 hoàn toàn tương đương với ISO 11843-2:2000 và Đính chính kỹ thuật 1:2007;
TCVN 10431-2:2014 do Ban kỹ thuật tiêu chuẩn quốc gia TCVN/TC 69 Ứng dụng các phương pháp thống kê biên soạn, Tổng cục Tiêu chuẩn Đo lường Chất lượng đề nghị, Bộ Khoa học và Công nghệ công bố.
Bộ TCVN 10431 (ISO 11843), Năng lực phát hiện, gồm các tiêu chuẩn sau:
- TCVN 10431-1:2014 (ISO 11843-1:1997), Phần 1: Thuật ngữ và định nghĩa;
- TCVN 10431-2:2014 (ISO 11843-2:2000), Phần 2: Phương pháp luận trong trường hợp hiệu chuẩn tuyến tính;
- TCVN 10431-3:2014 (ISO 11843-3:2003), Phần 3: Phương pháp luận xác định giá trị tới hạn đối với biến đáp ứng khi không sử dụng dữ liệu hiệu chuẩn;
- TCVN 10431-4:2014 (ISO 11843-4:2003), Phần 4: Phương pháp luận so sánh giá trị tối thiểu phát hiện được với giá trị đã cho;
- TCVN 10431-5:2014 (ISO 11843-5:2008), Phần 5: Phương pháp luận trong trường hợp hiệu chuẩn tuyến tính và phi tuyến;
- TCVN 10431-6:2014 (ISO 11843-6:2013), Phần 6: Phương pháp luận xác định giá trị tới hạn và giá trị tối thiểu phát hiện được trong phép đo có phân bố Poisson được xấp xỉ chuẩn;
- TCVN 10431-7:2014 (ISO 11843-7:2012), Phần 7: Phương pháp luận dựa trên tính chất ngẫu nhiên của nhiễu phương tiện đo.
Lời giới thiệu
Yêu cầu lý tưởng về năng lực phát hiện đối với biến trạng thái được lựa chọn là trạng thái thực tế của mọi hệ thống quan trắc có thể được phân loại chắc chắn là bằng hay khác với trạng thái cơ sở của nó. Tuy nhiên, do biến dạng hệ thống và ngẫu nhiên, yêu cầu lý tưởng này không thể đáp ứng được vì:
- trong thực tế, tất cả các trạng thái quy chiếu, bao gồm cả trạng thái cơ sở, đều không bao giờ được biết đối với biến trạng thái. Do đó, tất cả các trạng thái chỉ có thể được đặc trưng chính xác về những khác biệt so với trạng thái cơ sở, nghĩa là đối với biến trạng thái tịnh.
Trong thực tế, trạng thái quy chiếu thường được giả định là đã biết về biến trạng thái. Nói cách khác, giá trị của biến trạng thái đối với trạng thái cơ sở được đặt bằng “không”; ví dụ, trong hóa học phân tích, nồng độ hoặc lượng chưa biết của một mẫu phân tích trong mẫu trắng thường được giả định bằng “không” và giá trị của nồng độ tịnh hoặc lượng tịnh được báo cáo dưới dạng nồng độ hoặc lượng giả định. Đặc biệt, trong phân tích vết hóa học, chỉ có thể ước lượng những khác biệt về nồng độ hoặc lượng đối với mẫu trắng sẵn có. Để ngăn ngừa những quyết định sai, thường khuyến nghị chỉ báo cáo những khác biệt so với trạng thái cơ sở, nghĩa là dữ liệu đối với biến trạng thái tịnh;
CHÚ THÍCH: Trong TCVN 8890 (ISO Guide 30) và TCVN 9598 (ISO 11095) không đưa ra phân biệt giữa biến trạng thái và biến trạng thái tịnh. Kết quả là, trong hai tiêu chuẩn này, trạng thái quy chiếu được giả định là đã biết về biến trạng thái, không có lý giải.
- hiệu chuẩn và các quá trình lấy mẫu cũng như chuẩn bị mẫu đều bổ sung độ biến động ngẫu nhiên vào kết quả đo.
Trong tiêu chuẩn này, hai yêu cầu sau đây được lựa chọn:
- giá trị a là xác suất phát hiện (sai) rằng hệ thống không ở trạng thái cơ sở trong khi nó ở trạng thái cơ sở;
- giá trị b là xác suất không phát hiện (sai) rằng hệ thống, trong đó giá trị của biến trạng thái tịnh của hệ thống này bằng giá trị tối thiểu phát hiện được (xd), không ở trạng thái cơ sở.
NĂNG LỰC PHÁT HIỆN - PHẦN 2: PHƯƠNG PHÁP LUẬN TRONG TRƯỜNG HỢP HIỆU CHUẨN TUYẾN TÍNH
Capability of detection - Part 2: Methodology in the linear calibration case
Tiêu chuẩn này quy định các phương pháp cơ bản để:
- thiết kế thực nghiệm cho việc ước lượng giá trị tới hạn của biến trạng thái tịnh, giá trị tới hạn của biến đáp ứng và giá trị tối thiểu phát hiện được của biến trạng thái tịnh,
- ước lượng các đặc trưng này từ dữ liệu thực nghiệm cho các trường hợp trong đó hàm hiệu chuẩn là tuyến tính và độ lệch chuẩn là hằng số hoặc liên quan tuyến tính với biến trạng thái tịnh.
Các phương pháp mô tả trong tiêu chuẩn này áp dụng cho nhiều tình huống như kiểm tra sự có mặt của chất nào đó trong nguyên vật liệu, phát thải năng lượng từ mẫu hoặc thiết bị, hoặc thay đổi hình học trong hệ thống tĩnh bị biến dạng.
Giá trị tới hạn có thể được rút ra từ loạt phép đo thực tế để có thể đánh giá trạng thái chưa biết của hệ thống bao gồm trong loạt đó, trong khi giá trị tối thiểu phát hiện được của biến trạng thái tịnh như đặc trưng của phương pháp đo dùng cho việc lựa chọn các quá trình đo thích hợp. Để mô tả đặc trưng một quá trình đo, phương pháp phòng thí nghiệm hoặc phương pháp đo, giá trị tối thiểu phát hiện được có thể được nêu rõ nếu sẵn có dữ liệu thích hợp cho mỗi cấp độ liên quan, nghĩa là loạt phép đo, quá trình đo, phương pháp phòng thí nghiệm hoặc phương pháp đo. Giá trị tối thiểu phát hiện được có thể khác biệt đối với loạt phép đo, quá trình đo, phương pháp phòng thí nghiệm hoặc phương pháp đo.
Bộ TCVN 10431 (ISO 11843) áp dụng cho các đại lượng đo được trên các thang đo về cơ bản là liên tục. Bộ tiêu chuẩn này áp dụng cho các quá trình đo và các loại thiết bị đo trong đó mối quan hệ hàm số giữa giá trị kỳ vọng của biến đáp ứng và giá trị của biến trạng thái được mô tả bằng hàm hiệu chuẩn. Nếu biến đáp ứng hoặc biến trạng thái là đại lượng véctơ thì các phương pháp của bộ tiêu chuẩn này được áp dụng riêng cho các thành phần véctơ hoặc hàm số của các thành phần.
Các tài liệu viện dẫn trong tiêu chuẩn này rất cần thiết cho việc áp dụng tiêu chuẩn. Đối với các tài liệu có ghi năm công bố thì áp dụng bản được nêu. Đối với các tài liệu không ghi năm công bố thì áp dụng phiên bản mới nhất, bao gồm cả các sửa đổi.
TCVN 8244-1 (ISO 3534-1), Thống kê học - Từ vựng và ký hiệu - Phần 1: Thuật ngữ chung về thống kê và thuật ngữ dùng trong xác suất.
TCVN 8244-2 (ISO 3534-2), Thống kê học - Từ vựng và ký hiệu - Phần 2: Thống kê ứng dụng.
ISO 3534-3:1999, Statistics - Vocabulary and symbols - Part 3: Design of experiments (Thống kê học - Từ vựng và ký hiệu - Phần 3: Thiết kế thực nghiệm)
TCVN 9598:2013 (ISO 11095:1996), Hiệu chuẩn tuyến tính sử dụng mẫu chuẩn.
TCVN 10431-1:2014 (ISO 11843-1:1997), Năng lực phát hiện - Phần 1: Thuật ngữ và định nghĩa.
TCVN 8890:2011 (ISO Guide 30:1992), Thuật ngữ và định nghĩa sử dụng cho mẫu chuẩn.
Tiêu chuẩn này áp dụng các thuật ngữ và định nghĩa trong TCVN 8244 (ISO 3534) (tất cả các phần), TCVN 8890 (ISO Guide 30), TCVN 9598 (ISO 11095) và TCVN 10431-1 (ISO 11843-1).
4.1. Quy định chung
Quy trình xác định giá trị của trạng thái thực tế chưa biết bao gồm việc lấy mẫu, chuẩn bị và đo. Vì từng bước của quy trình này có thể tạo ra biến dạng, nên cần phải áp dụng cùng một quy trình cho việc mô tả đặc trưng, cho sử dụng trong chuẩn bị và xác định giá trị chưa biết của trạng thái thực tế, cho tất cả các trạng thái quy chiếu và trạng thái cơ sở sử dụng cho hiệu chuẩn.
Đối với mục đích xác định khác biệt giữa các giá trị đặc trưng cho một hoặc nhiều trạng thái thực tế chưa biết và trạng thái cơ sở, cần chọn một thiết kế thực nghiệm phù hợp để so sánh. Các đơn vị thực nghiệm của một thực nghiệm như vậy thu được từ trạng thái thực tế cần được đo và tất cả các trạng thái quy chiếu sử dụng cho hiệu chuẩn. Thiết kế lý tưởng sẽ duy trì không đổi tất cả các yếu tố đã biết là có ảnh hưởng tới kết quả và kiểm soát các yếu tố chưa biết bằng cách đưa ra thứ tự đã được ngẫu nhiên hóa để chuẩn bị và thực hiện các phép đo.
Trong thực tế, có thể khó thực hiện theo cách như vậy, vì việc chuẩn bị và xác định giá trị của trạng thái liên quan được thực hiện liên tục trong một khoảng thời gian. Tuy nhiên, để phát hiện độ chệch lớn thay đổi theo thời gian, đặc biệt khuyến nghị thực hiện một nửa hiệu chuẩn trước và một nửa sau phép đo trạng thái chưa biết. Tuy nhiên, điều này chỉ thực hiện được nếu đã biết trước cỡ của loạt phép đo và nếu có đủ thời gian để áp dụng cách này. Nếu không thể kiểm soát mọi yếu tố ảnh hưởng thì phải thể hiện các tuyên bố điều kiện bao gồm tất cả các giả định chưa chứng minh.
Nhiều phương pháp đo đòi hỏi xử lý mẫu về mặt hóa học hoặc vật lý trước khi đo. Cả hai bước này của quy trình đo đều làm tăng thêm độ biến động vào kết quả đo. Nếu cần lặp lại phép đo thì việc lặp lại bao gồm lặp lại đầy đủ việc chuẩn bị và đo. Tuy nhiên, trong nhiều tình huống, quy trình đo không được lặp lại đầy đủ, cụ thể là không phải tất cả các bước chuẩn bị đều được lặp lại cho từng phép đo; xem Chú thích trong 5.2.1.
4.2. Chọn trạng thái quy chiếu
Phạm vi giá trị của biến trạng thái tịnh được mở rộng bởi trạng thái quy chiếu cần bao gồm
- giá trị “không” của biến trạng thái tịnh, trong hóa phân tích nghĩa là mẫu trắng, và
- ít nhất một giá trị gần với giá trị dự kiến nhờ thông tin trước đó về giá trị tối thiểu phát hiện được; nếu yêu cầu này không được đáp ứng, thực nghiệm hiệu chuẩn cần được lặp lại với các giá trị khác của biến trạng thái tịnh, khi thích hợp.
Trạng thái quy chiếu cần được chọn sao cho giá trị của biến trạng thái tịnh (bao gồm các giá trị theo thang logarit) xấp xỉ cách đều nhau trong phạm vi giữa giá trị nhỏ nhất và giá trị lớn nhất.
Trong trường hợp trạng thái quy chiếu được thể hiện bằng việc chuẩn bị mẫu chuẩn thì thành phần của chúng nên càng gần với thành phần của vật liệu được đo càng tốt.
4.3. Chọn số lượng trạng thái quy chiếu, I, và (số lượng) lặp lại quy trình, J, K và L
Việc lựa chọn trạng thái quy chiếu, số mẫu chuẩn bị và số phép đo lặp lại phải như sau:
- số trạng thái quy chiếu I sử dụng trong thực nghiệm hiệu chuẩn ít nhất phải là 3; tuy nhiên, khuyến nghị I = 5;
- số mẫu chuẩn bị cho từng trạng thái quy chiếu J (bao gồm cả trạng thái cơ sở) cần giống nhau; khuyến nghị ít nhất là hai mẫu chuẩn bị (J = 2);
- số mẫu chuẩn bị cho trạng thái thực tế K cần bằng số mẫu chuẩn bị J cho từng trạng thái quy chiếu;
- số phép đo lặp lại L thực hiện trên mỗi mẫu chuẩn bị phải giống nhau; khuyến nghị ít nhất là hai phép đo lặp lại (L = 2);
CHÚ THÍCH: Công thức cho giá trị tới hạn và giá trị tối thiểu phát hiện được trong Điều 5 chỉ có giá trị với giả định là số phép đo lặp lại trên mỗi mẫu chuẩn bị là giống nhau đối với tất cả các phép đo trạng thái quy chiếu và trạng thái thực tế.
Vì sự biến động và chi phí do mẫu chuẩn bị thường sẽ cao hơn nhiều so với việc đo, nên lựa chọn tối ưu J, K và L có thể rút ra từ việc tối ưu hóa các ràng buộc liên quan đến sự biến động và chi phí.
5. Giá trị tới hạn yc và xc và giá trị tối thiểu phát hiện được xd của loạt phép đo
5.1. Giả định cơ bản
Các quy trình tính toán giá trị tới hạn và giá trị tối thiểu phát hiện được dưới đây dựa trên các giả định của TCVN 9598 (ISO 11095). Các phương pháp của TCVN 9598 (ISO 11095) được sử dụng với một tổng quát hóa; xem 5.3.
Các giả định cơ bản của TCVN 9598 (ISO 11095) là
- hàm hiệu chuẩn tuyến tính,
- phép đo biến đáp ứng của tất cả các mẫu chuẩn bị và trạng thái quy chiếu được giả định là độc lập và phân bố chuẩn với độ lệch chuẩn được đề cập là “độ lệch chuẩn dư”,
- độ lệch chuẩn dư là hằng số, nghĩa là không phụ thuộc vào giá trị của biến trạng thái tịnh [trường hợp 1] hoặc hình thành một hàm tuyến tính của các giá trị của biến trạng thái tịnh [trường hợp 2].
Quyết định liên quan đến khả năng áp dụng của tiêu chuẩn này và việc lựa chọn một trong hai trường hợp này cần dựa vào hiểu biết trước đó và kiểm tra bằng mắt các dữ liệu.
5.2. Trường hợp 1 - Độ lệch chuẩn không đổi
5.2.1. Mô hình
Mô hình sau đây dựa trên giả định về tính tuyến tính của hàm hiệu chuẩn và độ lệch chuẩn không đổi và được cho bởi:
Yij = a + bxi + eij (1)
trong đó
xi là ký hiệu của biến trạng thái tịnh ở trạng thái i;
eij là biến ngẫu nhiên mô tả thành phần ngẫu nhiên của sai số lấy mẫu, chuẩn bị và đo.
Giả định rằng eij độc lập và phân bố chuẩn với kỳ vọng “không” và độ lệch chuẩn dư lý thuyết s: eij ~ N(0; s2). Do đó, giá trị Yij của biến đáp ứng là biến ngẫu nhiên với kỳ vọng E(Yij) = a + bxi và phương sai V(Yij) = s2; không phụ thuộc vào xi.
CHÚ THÍCH: Trong trường hợp J mẫu được chuẩn bị cho phép đo và mỗi mẫu được đo L lần sao cho J·L phép đo được thực hiện đối với trạng thái quy chiếu i, khi đó Yij đề cập đến trung bình của L phép đo thu được trên mẫu được chuẩn bị.
5.2.2. Ước lượng của hàm hiệu chuẩn và độ lệch chuẩn dư
Theo TCVN 9598 (ISO 11095), ước lượng (xem chú thích) của a, b và s2 được cho bởi:
|
| (2) |
|
| (3) |
|
| (4) |
Các ký hiệu sử dụng ở đây và những nơi khác trong tiêu chuẩn này được liệt kê trong Phụ lục A.
CHÚ THÍCH: Các ước lượng được ký hiệu bằng dấu ^ để phân biệt chúng với bản thân các tham số chưa biết.
5.2.3. Tính giá trị tới hạn
Giá trị tới hạn của biến đáp ứng được cho bởi:
|
| (5) |
| Giá trị tới hạn của biến trạng thái tịnh được cho bởi: | |
|
| (6) |
t0,95(v) là phân vị 95 % của phân bố t với v = I × J - 2 bậc tự do.
Dẫn xuất của các công thức này được cho trong Phụ lục B.
5.2.4. Tính giá trị tối thiểu phát hiện được
Giá trị tối thiểu phát hiện được được cho bởi:
|
| (7) |
trong đó
d = (v; a, b) là giá trị của tham số không trung tâm xác định sao cho biến ngẫu nhiên có phân bố t không trung tâm với v = I × J - 2 bậc tự do và tham số không trung tâm d, T (v; d), thỏa mãn phương trình:
P [T(v; d) ≤ t1-a (v)] = b
trong đó t1-a (v) là phân vị (1 - a) của phân bố t với v bậc tự do.
Dẫn xuất của công thức này được cho trong Phụ lục B.
Đối với a = b và v > 3, phép xấp xỉ tốt cho d được cho bởi
d(v; a, b) » 2t1-a(v) (8)
nếu v = 4 và a = b = 0,05, sai số tương đối của phép xấp xỉ này là 5 %; t1-a(v) là phân vị (1 - a) của phân bố t với v = I × J - 2 bậc tự do.
Bảng 1 trình bày d(v; a, b) đối với a = b = 0,05 và các giá trị khác nhau của v.
Đối với a = b và v > 3, xd xấp xỉ bằng
|
| (9) |
Bảng 1 - Giá trị của tham số không trung tâm đối với a = b = 0,05 và v bậc tự do
| v | d(v; a, b) | V | d(v; a, b) | V | d(v; a, b) |
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | 5,516 4,456 4,067 3,870 3,752 3,673 3,617 3,575 3,543 3,517 3,496 3,479 3,464 3,451 3,440 3,431 3,422 | 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | 3,415 3,408 3,402 3,397 3,392 3,387 3,383 3,380 3,376 3,373 3,370 3,367 3,365 3,362 3,360 3,358 3,356 | 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 | 3,354 3,352 3,350 3,349 3,347 3,346 3,344 3,343 3,342 3,341 3,339 3,338 3,337 3,336 3,335 |
5.3. Trường hợp 2 - Độ lệch chuẩn phụ thuộc tuyến tính vào biến trạng thái tịnh
5.3.1. Mô hình
Mô hình sau đây dựa trên giả định rằng hàm hiệu chuẩn là tuyến tính và độ lệch chuẩn phụ thuộc tuyến tính vào biến trạng thái tịnh và được cho bởi:
Yij = a + bxi + eij (10)
trong đó
xi, a, b và Yij như định nghĩa ở 5.2.1 và eij là độc lập và có phân bố chuẩn với kỳ vọng E(eij) = 0 và phương sai:
V(eij)= s2(xi)= (c + dxi)2 (11)
nghĩa là, độ lệch chuẩn dư phụ thuộc tuyến tính vào x
s(xi) = c + dxi (12)
Các tham số của mô hình, a, b, c và d được ước lượng theo quy trình gồm hai phần như nêu trong 5.3.2 và 5.3.3.
5.3.2. Ước lượng của quan hệ tuyến tính giữa độ lệch chuẩn dư và biến trạng thái tịnh
Các tham số c và d được ước lượng bằng phân tích hồi quy tuyến tính với độ lệch chuẩn:
|
| (13) |
khi các giá trị của biến độc lập S và với biến trạng thái tịnh x là biến độc lập. Vì phương sai V(S) tỷ lệ với s2 nên phân tích hồi quy có trọng số (xem tài liệu tham khảo [1] và [2] trong Thư mục tài liệu tham khảo) được thực hiện với các trọng số:
|
| (14) |
Tuy nhiên, các phương sai s2(xi) phụ thuộc vào tham số chưa biết c và d vẫn chưa được ước lượng. Do đó, quy trình lặp lại với các trọng số sau đây được đề xuất:
|
| (15) |
Ở lần lặp đầu tiên, (q = 0), ![]() , trong đó các giá trị si là độ lệch chuẩn thực nghiệm. Đối với các lần lặp liên tiếp q = 1, 2,…
, trong đó các giá trị si là độ lệch chuẩn thực nghiệm. Đối với các lần lặp liên tiếp q = 1, 2,…
tính với các giá trị phụ trợ:
|
| (16) |
|
| (17) |
| và |
|
|
| (18) |
| và |
|
|
| (19) |
Quy trình này hội tụ nhanh để có kết quả cho q = 3;
![]() ;
;
có thể được xét với ![]()
![]() và
và ![]() , thành kết quả cuối cùng:
, thành kết quả cuối cùng:
![]() (20)
(20)
5.3.3. Ước lượng của hàm hiệu chuẩn
Các tham số a và b được ước lượng bằng phân tích hồi quy tuyến tính có trọng số (xem tài liệu tham khảo [1] và [2] trong Thư mục tài liệu tham khảo) với ![]() là các giá trị của biến độc lập, xi là các giá trị của biến độc lập và các trọng số:
là các giá trị của biến độc lập, xi là các giá trị của biến độc lập và các trọng số:
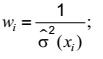
trong đó
![]() là giá trị dự đoán của phương sai tại xi theo công thức (20)
là giá trị dự đoán của phương sai tại xi theo công thức (20)
với:
|
| (21) |
các ước lượng cho a và b là:
|
| (22) |
|
| (23) |
5.3.4. Tính toán giá trị tới hạn
Giá trị tới hạn của biến đáp ứng được cho bởi:
|
| (24) |
và giá trị tới hạn của biến trạng thái tịnh được cho bởi:
|
| (25) |
trong đó
|
| (26) |
|
| (27) |
|
| (28) |
và t0,95(v) là phân vị 95 % của phân bố t với v = I×J - 2 bậc tự do; sxxw được xác định trong Phụ lục A.
5.3.5. Tính toán giá trị tối thiểu phát hiện được
Giá trị tối thiểu phát hiện được được cho bởi:
|
| (29) |
trong đó
d = d(v; a; b) là giá trị của tham số không trung tâm như xác định ở 5.2.4.
Vì ![]() phụ thuộc vào giá trị của xd chưa được tính toán, nên xd phải được tính lặp lại.
phụ thuộc vào giá trị của xd chưa được tính toán, nên xd phải được tính lặp lại.
Phép lặp bắt đầu với ![]() và cho xd0; đối với bước lặp tiếp theo
và cho xd0; đối với bước lặp tiếp theo ![]() được tính và sử dụng trong công thức dùng cho xd, dẫn đến xd1,… Trong nhiều trường hợp, ngay ở bước lặp đầu tiên không làm thay đổi đáng kể giá trị của xd; giá trị chấp nhận được đối với xd thu được ở bước lặp thứ ba.
được tính và sử dụng trong công thức dùng cho xd, dẫn đến xd1,… Trong nhiều trường hợp, ngay ở bước lặp đầu tiên không làm thay đổi đáng kể giá trị của xd; giá trị chấp nhận được đối với xd thu được ở bước lặp thứ ba.
6. Giá trị tối thiểu phát hiện được của phương pháp đo
Giá trị tối thiểu phát hiện được thu được từ hiệu chuẩn cụ thể cho thấy năng lực của quá trình đo được hiệu chuẩn đối với loạt phép đo tương ứng để phát hiện giá trị của biến trạng thái tịnh của trạng thái thực tế quan sát là khác “không”, nghĩa là, đây là giá trị nhỏ nhất của biến trạng thái tịnh có thể phát hiện được với xác suất 1 - b là khác “không”. Giá trị tối thiểu phát hiện được này khác nhau đối với các hiệu chuẩn khác nhau. Giá trị tối thiểu phát hiện được của các loạt phép đo khác nhau đối với
- quá trình đo cụ thể dựa trên cùng một loại quá trình đo,
- loại quá trình đo dựa trên cùng một phương pháp đo, hoặc
- phương pháp đo
có thể được giải thích là sự thể hiện của biến ngẫu nhiên mà đối với nó các tham số của phân bố xác suất có thể được coi là đặc trưng của quá trình đo, loại quá trình đo hoặc phương pháp đo, tương ứng.
Nếu đối với một quá trình đo cụ thể, m hiệu chuẩn liên tiếp được thực hiện để xác định giá trị tối thiểu phát hiện được của biến trạng thái tịnh xd, thì m giá trị tối thiểu phát hiện được xd1, xd2, …, xdm, có thể được sử dụng để xác định giá trị tối thiểu phát hiện được của quá trình đo trong các điều kiện sau đây:
a) quá trình đo không thay đổi;
b) phân bố của các giá trị xd là một mốt và không có giá trị xd bất thường;
c) thiết kế thực nghiệm (bao gồm số trạng thái quy chiếu, I, và số lần lặp lại quy trình, J, K và L) giống nhau đối với mỗi hiệu chuẩn.
Trong những điều kiện này, trung vị của các giá trị xd, đối với i = 1, …, m được khuyến nghị là giá trị tối thiểu phát hiện được của quá trình đo; nếu thống kê tổng hợp khác của các giá trị xdi được sử dụng thay cho trung vị thì thống kê đó phải được báo cáo.
Nếu vi phạm bất kỳ điều nào trong các điều kiện này thì giá trị tối thiểu phát hiện được của quá trình đo không được xác định đủ tốt và không được cố gắng xác định một giá trị chung.
Nếu cùng một phương pháp đo được áp dụng ở p phòng thí nghiệm và cần xác định giá trị tối thiểu phát hiện được của quá trình đo trong phạm vi phòng thí nghiệm cho mỗi phòng thí nghiệm thì, trong các điều kiện giống như đối với việc xác định giá trị tối thiểu phát hiện được của quá trình đo, khuyến nghị sử dụng trung vị của p giá trị tối thiểu phát hiện được của các phòng thí nghiệm làm giá trị tối thiểu phát hiện được của phương pháp đo; nếu thống kê tổng hợp khác của các giá trị tối thiểu phát hiện được của phòng thí nghiệm được sử dụng thay cho trung vị thì thống kê đó phải được báo cáo.
7. Báo cáo và sử dụng các kết quả
CHÚ THÍCH: Ví dụ về việc xác định giá trị phát hiện được tới hạn và nhỏ nhất được nêu trong Phụ lục C.
7.1. Giá trị tới hạn
Đối với các quyết định liên quan đến nghiên cứu trạng thái thực tế, chỉ áp dụng giá trị tới hạn của biến trạng thái tịnh hoặc của biến đáp ứng. Các giá trị này được rút ra từ hiệu chuẩn quá trình đo là các giới hạn quyết định được sử dụng để đánh giá trạng thái chưa biết của hệ thống bao gồm trong loạt này. Xem xét các hiệu chuẩn liên tiếp của cùng một quá trình đo, giá trị tới hạn có thể khác nhau giữa các hiệu chuẩn. Tuy nhiên, vì mỗi giá trị tới hạn là một giới hạn quyết định thuộc về một loạt phép đo cụ thể nên sẽ không có ý nghĩa khi tính giá trị tới hạn tổng thể trong các hiệu chuẩn và cũng không thích hợp khi sử dụng chúng làm các giá trị tới hạn.
Nếu giá trị của biến trạng thái tịnh hoặc của biến đáp ứng không lớn hơn giá trị tới hạn thì có thể tuyên bố là không thấy sự khác biệt giữa trạng thái thực tế quan sát được với trạng thái cơ sở. Tuy nhiên, do khả năng có thể mắc phải sai lầm loại hai, giá trị này không nên được hiểu là chứng tỏ rằng hệ thống được quan trắc hoàn toàn ở trạng thái cơ sở của nó. Do đó, việc báo cáo kết quả như vậy là “không” hoặc “nhỏ hơn giá trị tối thiểu phát hiện được” là không được phép. Giá trị (và độ không đảm bảo của nó) cần được được báo cáo; nếu nó không vượt quá giá trị tới hạn thì cần bổ sung bình luận “không phát hiện được”.
7.2. Giá trị tối thiểu phát hiện được
Giá trị tối thiểu phát hiện được rút ra từ một hiệu chuẩn cụ thể cho thấy năng lực phát hiện của quá trình đo thực tế có đủ cho mục đích dự kiến hay không. Nếu như không đủ thì có thể sửa đổi số J, K hoặc L.
Giá trị tối thiểu phát hiện được rút ra từ một tập hợp các hiệu chuẩn trong các điều kiện đề cập ở Điều 6 có thể được dùng để so sánh, lựa chọn hoặc đánh giá các phòng thử nghiệm hoặc phương pháp khác nhau, tương ứng.
| a | hệ số chặn trong biểu thức y = a + bx + e |
|
| ước lượng của hệ số chặn a |
| b | độ dốc trong biểu thức y = a + bx + e |
|
| ước lượng của độ dốc b |
| c | hệ số chặn trong biểu thức s(x)= c + dx đối với độ lệch chuẩn dư |
|
| ước lượng của hệ số chặn c |
| d | độ dốc trong biểu thức s(x) = c + dx đối với độ lệch chuẩn dư |
|
| ước lượng của độ dốc d |
| E ( ) | kỳ vọng (của biến ngẫu nhiên cho trong ngoặc) |
| I | số trạng thái quy chiếu dùng trong thực nghiệm hiệu chuẩn |
| I = 1, …, I | biến xác định của các trạng thái quy chiếu |
| J | số mẫu chuẩn bị cho từng trạng thái quy chiếu |
| j = 1, …, J | biến xác định của các mẫu chuẩn bị đối với trạng thái quy chiếu và trạng thái cơ sở |
| K | số mẫu chuẩn bị cho trạng thái thực tế |
| k = 1, …, K | biến xác định của các mẫu chuẩn bị đối với trạng thái thực tế |
| L | số phép đo lặp lại cho từng mẫu chuẩn bị |
| l = 1, …, L | biến xác định của các phép đo lặp lại đối với mỗi mẫu chuẩn bị |
| M | hệ số nhân |
| m | số hiệu chuẩn liên tiếp |
| N | số mẫu chuẩn bị trong thực nghiệm hiệu chuẩn; nếu số mẫu chuẩn bị cho từng trạng thái quy chiếu là giống nhau thì N = I×J, và tổng số phép đo trong thực nghiệm hiệu chuẩn là N×L |
| q = 0, 1, 2, … | số bước lặp lại |
| s | độ lệch chuẩn thực nghiệm |
|
| tổng độ lệch chuẩn bình phương các giá trị được chọn của biến trạng thái tịnh đối với trạng thái quy chiếu (bao gồm cả trạng thái cơ sở) so với giá trị trung bình |
|
| tổng độ lệch chuẩn bình phương có trọng số các giá trị được chọn của biến trạng thái tịnh đối với trạng thái quy chiếu (bao gồm cả trạng thái cơ sở) so với giá trị trung bình có trọng số |
| T | giá trị phụ trợ đối với phân tích hồi quy tuyến tính có trọng số |
| V ( ) | phương sai (của biến ngẫu nhiên cho trong ngoặc) |
| wi | trọng số tại xi |
|
| trọng số tại xi ở bước lặp thứ q |
| X | biến trạng thái tịnh, X = Z - z0 |
| x | giá trị cụ thể của biến trạng thái tịnh |
| x1, …, xI | giá trị được chọn của biến trạng thái tịnh X đối với trạng thái quy chiếu bao gồm cả trạng thái cơ sở |
| xc | giá trị tới hạn của biến trạng thái tịnh |
| xd | giá trị tối thiểu phát hiện được của biến trạng thái tịnh |
|
| trung bình các giá trị được chọn của biến trạng thái tịnh đối với trạng thái quy chiếu (bao gồm cả trạng thái cơ sở) |
|
| giá trị ước lượng của biến trạng thái tịnh đối với trạng thái thực tế cụ thể |
|
| trung bình có trọng số các giá trị được chọn của biến trạng thái tịnh đối với trạng thái quy chiếu (bao gồm cả trạng thái cơ sở) |
| Y | biến đáp ứng |
| yc | giá trị tới hạn của biến đáp ứng |
| yijl | phép đo thứ l của mẫu chuẩn bị thứ j của trạng thái quy chiếu thứ i |
| yk1, …, ykl | giá trị thu được của biến đáp ứng đối với mẫu chuẩn bị thứ k của trạng thái thực tế cụ thể trong loạt phép đo |
|
| trung bình các giá trị quan trắc đối với trạng thái thực tế cụ thể |
|
| trung bình các giá trị đo yijl |
|
| trung bình các giá trị đo của mẫu chuẩn bị thứ j của trạng thái quy chiếu thứ i |
|
| trung bình các giá trị đo của trạng thái quy chiếu thứ i |
|
| trung bình các giá trị đo K × L tại x = 0 |
| Z | biến trạng thái |
| z0 | giá trị của biến trạng thái trong trạng thái quy chiếu |
| a | xác suất bác bỏ sai giả thuyết không “trạng thái đang xét không khác với trạng thái cơ sở đối với biến trạng thái” cho mỗi trạng thái thực tế quan trắc được trong loạt đo trong khi giả thuyết không này là đúng (xác suất sai lầm loại một) khi không có khuyến nghị cụ thể, giá trị của a cần được cố định ở a = 0,05 |
| b | xác suất chấp nhận sai giả thuyết không “trạng thái đang xét không khác với trạng thái cơ sở đối với biến trạng thái” cho mỗi trạng thái thực tế quan trắc được trong loạt đo trong đó biến trạng thái tịnh bằng giá trị tối thiểu phát hiện được cần xác định (xác suất sai lầm loại hai) khi không có khuyến nghị cụ thể, giá trị của b cần được cố định ở b = 0,05 |
| d | tham số không trung tâm của phân bố t không trung tâm |
| e | thành phần của phép đo biến đáp ứng thể hiện thành phần ngẫu nhiên của sai số lấy mẫu, chuẩn bị và đo |
| v | bậc tự do |
| sdiff | độ lệch chuẩn của hiệu giữa trung bình, |
|
| ước lượng của độ lệch chuẩn dư |
|
| độ lệch chuẩn tại xi ở bước lặp thứ q |
|
| ước lượng của độ lệch chuẩn dư, x = 0 |
|
|
|
B.1. Trường hợp 1 - Độ lệch chuẩn không đổi
Với các giả định của 5.1 và trong trường hợp độ lệch chuẩn không đổi, ước lượng của hệ số hồi quy, ![]() và
và ![]() , được phân bố chuẩn với kỳ vọng
, được phân bố chuẩn với kỳ vọng
E(![]() ) = a; E(
) = a; E(![]() ) = b
) = b
và phương sai:
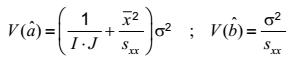
trong đó
s2 là phương sai dư của trung bình của L phép đo lặp lại đối với mỗi mẫu chuẩn bị.
Nếu biến đáp ứng được đo K×L lần ở trạng thái cơ sở (z = z0, x = 0) thì hiệu giữa trung bình ![]() của K·L giá trị và ước lượng của hệ số chặn
của K·L giá trị và ước lượng của hệ số chặn ![]() tuân theo phân bố chuẩn với kỳ vọng:
tuân theo phân bố chuẩn với kỳ vọng:
![]()
và phương sai:
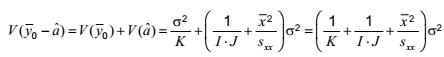
Vì ![]() được phân bố chuẩn nên biến ngẫu nhiên
được phân bố chuẩn nên biến ngẫu nhiên
![]()
tuân theo phân bố chuẩn chuẩn hóa, và bất đẳng thức:
![]()
vẫn đúng với xác suất 0,95. Vì ![]() chưa biết nên có thể ước lượng là:
chưa biết nên có thể ước lượng là:
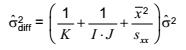
trong đó
![]() là phương sai dư ước lượng của phân tích hồi quy được sử dụng thay thế. Biến ngẫu nhiên
là phương sai dư ước lượng của phân tích hồi quy được sử dụng thay thế. Biến ngẫu nhiên
![]()
tuân theo phân bố t với v = I × J - 2 bậc tự do, và bất đẳng thức:
![]()
hoặc
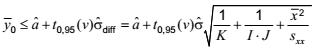
trong đó
t0,95(v) là phân vị 95 % của phân bố t với v bậc tự do, đúng với xác suất 0,95.
Vế phải của bất đẳng thức này là giá trị tới hạn của biến đáp ứng
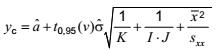
và giá trị tới hạn của biến trạng thái tịnh là
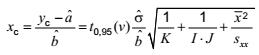
Các biểu thức tương tự mô tả giá trị này khi các phân vị khác của phân bố t là thích hợp.
Để xác định giá trị tối thiểu phát hiện được xd của biến trạng thái tịnh, cần kiểm tra phân bố của ![]() trong trường hợp giá trị thực x của biến trạng thái tịnh giống hệt giá trị tối thiểu phát hiện được xd của biến trạng thái tịnh, x = xd. Cần phát hiện trạng thái này với xác suất 1 - b, nghĩa là:
trong trường hợp giá trị thực x của biến trạng thái tịnh giống hệt giá trị tối thiểu phát hiện được xd của biến trạng thái tịnh, x = xd. Cần phát hiện trạng thái này với xác suất 1 - b, nghĩa là:
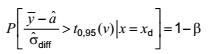
hoặc
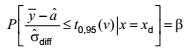
Nếu x = xd, kỳ vọng của ![]() là:
là:
![]()
và do đó:
![]()
trong khi:
![]()
như đối với x = 0.
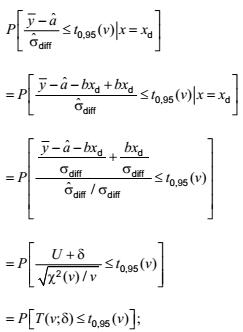
vì ![]() tuân theo phân bố chuẩn chuẩn hóa và
tuân theo phân bố chuẩn chuẩn hóa và ![]() độc lập với U tuân theo phân bố của
độc lập với U tuân theo phân bố của ![]() , biến ngẫu nhiên T(v,d) tuân theo phân bố t không trung tâm với v bậc tự do và tham số không trung tâm d; d = d (v;a;b) đối với a = 0,05 hoặc giá trị thích hợp khác, nếu yêu cầu được xác định như giá trị của tham số không trung tâm của phân bố t không trung tâm với v bậc tự do thỏa mãn:
, biến ngẫu nhiên T(v,d) tuân theo phân bố t không trung tâm với v bậc tự do và tham số không trung tâm d; d = d (v;a;b) đối với a = 0,05 hoặc giá trị thích hợp khác, nếu yêu cầu được xác định như giá trị của tham số không trung tâm của phân bố t không trung tâm với v bậc tự do thỏa mãn:
P[T(v,d) ≤ t1-a(v)] = b
Từ:
![]()
tuân thủ biểu thức sau:
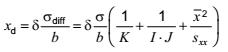
đối với giá trị tối thiểu phát hiện được của biến trạng thái tịnh.
Để dự đoán, ước lượng của b và s được đưa vào công thức sao cho giá trị tối thiểu phát hiện được được cho bởi:
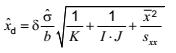
Giá trị tới hạn của biến đáp ứng yc là tổng của ![]() và bội của
và bội của ![]() , và giá trị tới hạn của biến trạng thái tịnh là bội của
, và giá trị tới hạn của biến trạng thái tịnh là bội của ![]() . Nếu, theo khuyến nghị, giá trị của biến trạng thái tịnh của trạng thái quy chiếu cách đều giá trị nhỏ nhất “không”, a = 0,05 và
. Nếu, theo khuyến nghị, giá trị của biến trạng thái tịnh của trạng thái quy chiếu cách đều giá trị nhỏ nhất “không”, a = 0,05 và
- K = 1 (một mẫu chuẩn bị cho phép đo trạng thái thực tế) hoặc
- K = J (số mẫu chuẩn bị cho phép đo trạng thái thực tế bằng số mẫu chuẩn bị cho phép đo trạng thái quy chiếu);
hệ số:
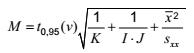
trong biểu thức đối với giá trị tới hạn chỉ là hàm số của số trạng thái quy chiếu, I, và số mẫu chuẩn bị của từng trạng thái quy chiếu, J. Đối với một số trường hợp M được cho trong Bảng B.1.
Bảng B.1 - Xác định hệ số nhân, M
| Đối với K = 1 | |||||
| I | J | I×J |
| t0,95(v) | M |
| 3 | 1 | 3 | 1,35 | 6,31 | 8,52 |
| 3 | 2 | 6 | 1,19 | 2,13 | 2,54 |
| 5 | 1 | 5 | 1,26 | 2,35 | 2,97 |
| 5 | 2 | 10 | 1,14 | 1,86 | 2,12 |
| 5 | 4 | 20 | 1,07 | 1,73 | 1,86 |
| Đối với K = J | |||||
| I | J | I×J |
| t0,95(v) | M |
| 3 | 1 | 3 | 1,35 | 6,31 | 8,54 |
| 3 | 2 | 6 | 0,96 | 2,13 | 2,04 |
| 5 | 1 | 5 | 1,26 | 2,35 | 2,97 |
| 5 | 2 | 10 | 0,89 | 1,86 | 1,66 |
| 5 | 4 | 20 | 0,63 | 1,73 | 1,09 |
B.2. Trường hợp 2 - Độ lệch chuẩn phụ thuộc tuyến tính vào biến trạng thái tịnh
Với các giả định của 5.1 và trong trường hợp độ lệch chuẩn phụ thuộc tuyến tính vào biến trạng thái tịnh, ước lượng của hệ số hồi quy, ![]() và
và ![]() , được phân bố chuẩn với kỳ vọng:
, được phân bố chuẩn với kỳ vọng:
![]()
và phương sai:
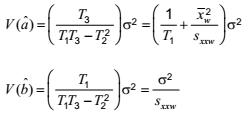
trong đó
s2 được xác định sao cho wis2 là phương sai dư của trung bình của L phép đo lặp lại đối với mẫu chuẩn bị i.
Nếu biến đáp ứng được đo K×L lần ở trạng thái cơ sở (Z = z0, X = 0) thì hiệu giữa trung bình ![]() của K×L giá trị và hệ số chặn ước lượng
của K×L giá trị và hệ số chặn ước lượng ![]() tuân theo phân bố chuẩn với kỳ vọng:
tuân theo phân bố chuẩn với kỳ vọng:
![]()
và phương sai:
![]()
![]() chưa biết nhưng có thể ước lượng như sau:
chưa biết nhưng có thể ước lượng như sau:
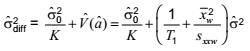
trong đó
![]() được lấy từ phương trình (20) và
được lấy từ phương trình (20) và ![]() là ước lượng phương sai dư của phân tích hồi quy có trọng số phải được sử dụng thay thế.
là ước lượng phương sai dư của phân tích hồi quy có trọng số phải được sử dụng thay thế.
Tương tự trường hợp 1, giá trị tới hạn của biến đáp ứng là:
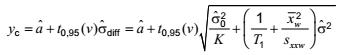
và giá trị tới hạn của biến trạng thái tịnh là
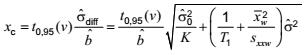
Các biểu thức tương tự mô tả giá trị này khi các phân vị khác của phân bố t là thích hợp.
Các công thức này bao gồm cả trường hợp độ lệch chuẩn không đổi trong đó tất cả các trọng số đều bằng một, wi = 1 đối với I = 1, …, I sao cho T1 = I × J, ![]() và
và ![]() .
.
Giá trị tối thiểu phát hiện được của biến trạng thái tịnh là:
![]()
trong đó, đối với x = xd,
![]()
Để dự đoán, ước lượng của b và ![]() và
và
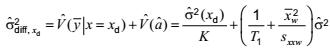
được đưa vào công thức sao cho giá trị tối thiểu phát hiện được của biến trạng thái tịnh được cho bởi:
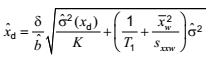
Vì ![]() phụ thuộc vào giá trị của xd chưa được tính nên phải sử dụng quy trình lặp lại của 5.3.5.
phụ thuộc vào giá trị của xd chưa được tính nên phải sử dụng quy trình lặp lại của 5.3.5.
C.1. Ví dụ 1
Hàm lượng thủy ngân, tính bằng ng/g1) nguyên liệu của nhà máy, được đo bằng máy quang phổ hấp thụ nguyên tử. Mỗi mẫu được phân tách bằng cách sử dụng kỹ thuật vi ba (MLS-1200) và hấp thụ trong dung dịch axit nitric/kali dicromat. Dung dịch này được kiểm tra thông qua hệ thống giảm hơi lạnh Varian VGA-76 dẫn đến hệ thống tập trung dạng lá mạ vàng (MCA-90) trước các phép đo hấp thụ nguyên tử lặp lại. Để ước lượng hàm hiệu chuẩn và để xác định năng lực phát hiện, mỗi trong số sáu mẫu quy chiếu thể hiện nồng độ trắng (x = 0) và nồng độ tịnh x = 0,2 ng/g; 0,5 ng/g; 1,0 ng/g; 2,0 ng/g; 3,0 ng/g được chuẩn bị ba mẫu, mỗi mẫu chuẩn bị được đo một lần. Do đó, I = 6; J = 3; L = 1.
Giả định rằng các giả thuyết về tính tuyến tính của hàm hiệu chuẩn, độ lệch chuẩn không đổi và phân bố chuẩn của biến đáp ứng là đúng; a và b được cố định trước ở giá trị a = b = 0,05. Đối với việc xác định hàm lượng thủy ngân trong nguyên liệu cần phân tích, có hai cách tiếp cận khác nhau được xét:
a) một phép đo sẽ được thực hiện (K = L = 1); hoặc
b) ba mẫu sẽ được chuẩn bị cho phép đo và mỗi mẫu được đo một lần (K = 3; L = 1) và trung bình ![]() của các giá trị quan trắc được sử dụng làm kết quả đo.
của các giá trị quan trắc được sử dụng làm kết quả đo.
Các kết quả thực nghiệm hiệu chuẩn được cho trong Bảng C.1.
Bảng C.1 - Kết quả của thực nghiệm hiệu chuẩn xác định hàm lượng thủy ngân trong thực phẩm hoặc thuốc
| Mẫu quy chiếu i | Hàm lượng thủy ngân tịnh xi ng/g | Độ hấp thụ yij | ||
| 1 2 3 4 5 6 | 0 0,2 0,5 1,0 2,0 3,0 | 0,003 0,004 0,011 0,023 0,048 0,071 | - 0,001 0,005 0,011 0,023 0,047 0,072 | 0,002 0,005 0,012 0,023 0,048 0,072 |
Phân tích thống kê thu được:
![]() = 1,116 7 ng/g
= 1,116 7 ng/g
sxx = 20,425
![]() = 9,995 9 x 10-5
= 9,995 9 x 10-5
![]() = 0,023 74
= 0,023 74
![]() = 1,109 9 x 10-3
= 1,109 9 x 10-3
Vì v = N - 2= 16;
t0,95 (v)= t0,95 (16) = 1,746;
d(v;a;b) = d(16;0,05;0,05) = 3,440;
(2 t0,95 (v) = 3,492)
Kết quả đối với cách tiếp cận a) là
giá trị tới hạn của biến đáp ứng [xem công thức (5)] yc = 0,002 15
giá trị tới hạn của hàm lượng tịnh [xem công thức (6)] xc = 0,086 ng/g
hàm lượng tịnh tối thiểu phát hiện được [xem công thức (9)] xd = 0,173 ng/g
- giá trị hấp thụ nhỏ nhất có thể được giải thích là thu được từ mẫu với hàm lượng thủy ngân tịnh lớn hơn hàm lượng mẫu trắng là yc = 0,002 15, giá trị tới hạn của biến đáp ứng;
- hàm lượng thủy ngân tịnh nhỏ nhất trong mẫu có thể phân biệt được (với xác suất 1 - b = 0,95) với hàm lượng mẫu trắng là xd = 0,173 ng/g, giá trị của hàm lượng tịnh tối thiểu phát hiện được.
Kết quả đối với cách tiếp cận b) là
giá trị tới hạn của biến đáp ứng [xem công thức (5)] yc = 0,001 40
giá trị tới hạn của hàm lượng tịnh [xem công thức (6)] xc = 0,055 ng/g
hàm lượng tịnh tối thiểu phát hiện được [xem công thức (9)] xd= 0,110 ng/g
C.2. Ví dụ 2 2)
Lượng toluen trong 100 ml phần chiết được đo bằng cách sử dụng sắc ký khí tiếp xúc với một máy dò đo phổ khối lượng (GC/MS). 100 ml mẫu được bơm vào hệ thống GC/MS. Sáu mẫu quy chiếu được sử dụng và chứa lượng toluen đã biết trong phạm vi từ 4,6 pg/100 ml đến 15 000 pg/100 ml. Mỗi mẫu được bơm và đo bốn lần (I = 6, J = 4, L = 1, N = 24). Kết quả đo được cho trong Bảng C.2.
Nhìn vào đồ thị thể hiện kết quả đo cho thấy quan hệ giữa lượng toluen và biến đáp ứng (diện tích đỉnh) là hoàn toàn tuyến tính; độ lệch chuẩn của diện tích đỉnh là tuyến tính phụ thuộc vào lượng toluen. Với giả định bổ sung về phân bố chuẩn của biến đáp ứng, có thể xác định năng lực phát hiện theo 5.3.
Bảng C.2 - Kết quả của thực nghiệm hiệu chuẩn đối với lượng toluen trong phần chiết 100 ml
| (1) Mẫu quy chiếu i | (2) Lượng toluen tịnh xi pg/100 ml | (3) Diện tích đỉnh
yij | (4) Độ lệch chuẩn thực nghiệm si | (5) | (6) | (7) | |||
| Độ lệch chuẩn dự đoán của phép lặp | |||||||||
| 1
| 2
| 1
| |||||||
| 1 2 3 4 5 6 | 4,6 23 116 580 3 000 15 000 | 29,80 44,60 207,70 894,67 5 350,65 20 718,14 | 16,85 48,13 222,40 821,30 4 942,63 24 781,61 | 16,68 42,27 172,88 773,40 4 315,79 22 405,76 | 19,52 34,78 207,51 936,93 3 879,28 24 863,91 | 6,20 5,65 21,02 73,19 652,98 2 005,02 | 4,56 7,07 19,73 82,91 412,46 2 046,54 | 5,17 7,93 21,87 91,43 454,22 2 253,14 | 5,15 7,92 21,88 91,57 455,02 2 257,23 |
Trong quy trình ước lượng c và d, tiến hành phân tích hồi quy tuyến tính có trọng số lặp theo 5.3.2 tạo ra các hàm hồi quy tuyến tính ước lượng sau đây:
lần lặp 1: ![]() = 3,933 23 + 0,136 174 xi
= 3,933 23 + 0,136 174 xi
lần lặp 2: ![]() = 4,482 84 + 0,149 911 xi
= 4,482 84 + 0,149 911 xi
lần lặp 3: ![]() = 4,462 28 + 0,150 185 xi
= 4,462 28 + 0,150 185 xi
Độ lệch chuẩn dự đoán tương ứng được cho trong các cột từ (5) đến (7) của Bảng C.2. Sau lần lặp thứ ba, các kết quả ổn định nên có thể sử dụng công thức của lần lặp 3 như kết quả cuối cùng của phần 1 của quy trình ước lượng, nghĩa là:
![]() = 4,462 28 + 0,150 185 x
= 4,462 28 + 0,150 185 x
![]() = 4,462 28
= 4,462 28
Các tham số a và b của hàm hiệu chuẩn được ước lượng bởi phân tích hồi quy tuyến tính có trọng số theo 5.3.3 với yij ở cột (3) là giá trị của biến phụ thuộc, xi của cột (2) là giá trị của biến độc lập và các trọng số:
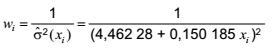
Phân tích hồi quy này cho:
![]() = 0,223 306
= 0,223 306
![]() = 15,566 9
= 15,566 9
sxxw = 606,224
![]() = 12,218 5
= 12,218 5
![]() = 1,527 27
= 1,527 27
![]() = 1,059 54
= 1,059 54
v = N - 2 = 22
t0,95(v) = t0,95 (22) = 1,717
Do đó, đối với K = 1, thu được giá trị sau đây:
giá trị tới hạn của biến đáp ứng [xem công thức (24)] yc = 20,82
giá trị tới hạn của lượng toluen tịnh trong 100 ml phần chiết [xem công thức (25)] xc = 5,63 pg.
Giá trị tối thiểu phát hiện được được tính lặp lại:
Đối với a = b = 0,05, d(v; a; b) = d(22; 0,05; 0,05) = 3,397 (xem Bảng 1) và với ![]() giá trị đầu tiên đối với xd [xem công thức (29)] là xd0 = 11,139; kéo theo
giá trị đầu tiên đối với xd [xem công thức (29)] là xd0 = 11,139; kéo theo ![]() = 6,135 2 và xd1 = 14,553;
= 6,135 2 và xd1 = 14,553;
với ![]() = 6,647 9 lần lặp 2 dẫn đến xd2 = 15,627 pg/100 ml và
= 6,647 9 lần lặp 2 dẫn đến xd2 = 15,627 pg/100 ml và
với ![]() = 6,809 2 cuối cùng ta có xd = xd3 = 15,967 pg/100 ml.
= 6,809 2 cuối cùng ta có xd = xd3 = 15,967 pg/100 ml.
Diện tích đỉnh nhỏ nhất có thể giải thích là thu được từ mẫu có nồng độ toluen tịnh lớn hơn nồng độ mẫu trắng là yc = 20,82, giá trị tới hạn của biến đáp ứng.
Lượng toluen tịnh nhỏ nhất trong mẫu chiết xuất 100 ml có thể phân biệt (với xác suất 1 - b = 0,95) so với nồng độ mẫu trắng là xd = 15,97 pg/100 ml, giá trị tối thiểu phát hiện được của nồng độ toluen tịnh.
Thư mục tài liệu tham khảo
[1] DRAPER N.R. và SMITH H. Phân tích hồi quy ứng dụng. Wiley, New York, 1981.
[2] MONTGOMERY D.C. và PECK E.A. Giới thiệu về phân tích hồi quy tuyến tính. Wiley, New York, 1992.
[3] CURRIE L.A. Thuật ngữ về đánh giá phương pháp phân tích bao gồm cả năng lực phát hiện và phẩm chất. Khuyến nghị của IUPAC 1995. Hóa học thuần túy và ứng dụng, 67, 1995, pp. 1699-1723.
MỤC LỤC
Lời nói đầu
Lời giới thiệu
1. Phạm vi áp dụng
2. Tài liệu viện dẫn
3. Thuật ngữ và định nghĩa
4. Thiết kế thực nghiệm
4.1. Quy định chung
4.2. Chọn trạng thái quy chiếu
4.3. Chọn số lượng trạng thái quy chiếu, I, và (số lượng) lặp lại quy trình, J, K và L
5. Giá trị tới hạn yc và xc và giá trị tối thiểu phát hiện được xd của loạt phép đo
5.1. Giả định cơ bản
5.2. Trường hợp 1 - Độ lệch chuẩn không đổi
5.3. Trường hợp 2 - Độ lệch chuẩn phụ thuộc tuyến tính vào biến trạng thái tịnh
6. Giá trị tối thiểu phát hiện được của phương pháp đo
7. Báo cáo và sử dụng các kết quả
7.1. Giá trị tới hạn
7.2. Giá trị tối thiểu phát hiện được
Phụ lục A (quy định) Ký hiệu và từ viết tắt
Phụ lục B (tham khảo) Dẫn xuất công thức
Phụ lục C (tham khảo) Ví dụ
Thư mục tài liệu tham khảo