NĂNG LỰC PHÁT HIỆN - PHẦN 5: PHƯƠNG PHÁP LUẬN TRONG TRƯỜNG HỢP HIỆU CHUẨN TUYẾN TÍNH VÀ PHI TUYẾN
Capability of detection - Part 5: Methodology in the linear and non-linear calibration cases
Lời nói đầu
TCVN 10431-5:2014 hoàn toàn tương đương với ISO 11843-5:2008;
TCVN 10431-5:2014 do Ban kỹ thuật tiêu chuẩn quốc gia TCVN/TC 69 Ứng dụng các phương pháp thống kê biên soạn, Tổng cục Tiêu chuẩn Đo lường Chất lượng đề nghị, Bộ Khoa học và Công nghệ công bố.
Bộ TCVN 10431 (ISO 11843), Năng lực phát hiện, gồm các tiêu chuẩn sau:
- TCVN 10431-1:2014 (ISO 11843-1:1997), Phần 1: Thuật ngữ và định nghĩa;
- TCVN 10431-2:2014 (ISO 11843-2:2000), Phần 2: Phương pháp luận trong trường hợp hiệu chuẩn tuyến tính;
- TCVN 10431-3:2014 (ISO 11843-3:2003), Phần 3: Phương pháp luận xác định giá trị tới hạn đối với biến đáp ứng khi không sử dụng dữ liệu hiệu chuẩn;
- TCVN 10431-4:2014 (ISO 11843-4:2003), Phần 4: Phương pháp luận so sánh giá trị tối thiểu phát hiện được với giá trị đã cho;
- TCVN 10431-5:2014 (ISO 11843-5:2008), Phần 5: Phương pháp luận trong trường hợp hiệu chuẩn tuyến tính và phi tuyến;
- TCVN 10431-6:2014 (ISO 11843-6:2013), Phần 6: Phương pháp luận xác định giá trị tới hạn và giá trị tối thiểu phát hiện được trong phép đo có phân bố Poisson được xấp xỉ chuẩn;
- TCVN 10431-7:2014 (ISO 11843-7:2012), Phần 7: Phương pháp luận dựa trên tính chất ngẫu nhiên của nhiễu phương tiện đo.
Lời giới thiệu
Trong thực tế có thể gặp cả hàm hiệu chuẩn tuyến tính và phi tuyến tính. Tiêu chuẩn này giải quyết hai trường hợp như nhau trong ngữ cảnh năng lực phát hiện, bằng việc quan tâm đến phân bố xác suất của biến trạng thái tịnh (đại lượng đo) chứ không phải là bản thân hàm hiệu chuẩn.
Các khái niệm cơ bản của TCVN 10431-2 (ISO 11843-2) bao gồm cả các yêu cầu xác suất, a và b, còn trường hợp hiệu chuẩn tuyến tính được đề cập trong tiêu chuẩn này. Trong khoảng giá trị giữa trạng thái cơ bản và giá trị tối thiểu phát hiện được, có thể áp dụng hàm hiệu chuẩn tuyến tính. Theo cách này, tính tương thích với TCVN 10431-2 (ISO 11843-2) được đảm bảo.
Trong trường hợp phương pháp phân tích được đặc trưng bởi hàm hiệu chuẩn tuyến tính được so sánh với phương pháp có hàm hiệu chuẩn phi tuyến, khuyến nghị sử dụng tiêu chuẩn này. Trong trường hợp hiệu chuẩn tuyến tính, có thể sử dụng cả TCVN 10431-2 (ISO 11843-2) và tiêu chuẩn này. TCVN 10431-2 (ISO 11843-2) sử dụng biên dạng độ chụm đối với riêng biến đáp ứng sẽ cho cùng một kết quả như tiêu chuẩn này, trong đó yêu cầu biên dạng độ chụm cả với biến đáp ứng và biến trạng thái tịnh, vì trong trường hợp tuyến tính biên dạng độ chụm đối với biến đáp ứng cũng giống như với biến trạng thái tịnh.
NĂNG LỰC PHÁT HIỆN - PHẦN 5: PHƯƠNG PHÁP LUẬN TRONG TRƯỜNG HỢP HIỆU CHUẨN TUYẾN TÍNH VÀ PHI TUYẾN
Capability of detection - Part 5: Methodology in the linear and non-linear calibration cases
Tiêu chuẩn này đề cập đến hàm hiệu chuẩn tuyến tính hoặc phi tuyến.
Tiêu chuẩn này quy định phương pháp cơ bản để
- xây dựng một biên dạng độ chụm cho biến đáp ứng, gọi là mô tả độ lệch chuẩn (SD) hoặc hệ số biến động (CV) của biến đáp ứng như hàm số của biến trạng thái tịnh,
- chuyển đổi biên dạng độ chụm này thành biên dạng độ chụm cho biến trạng thái tịnh kết hợp với hàm hiệu chuẩn, và
- sử dụng biên dạng độ chụm thu được để ước lượng giá trị tới hạn và giá trị tối thiểu phát hiện được của biến trạng thái tịnh.
Các phương pháp mô tả trong tiêu chuẩn này rất hữu ích cho việc kiểm tra phát hiện một chất nào đó bằng nhiều loại thiết bị đo khác nhau mà không thể áp dụng TCVN 10431-2 (ISO 11843-2). Trong đó bao gồm cả việc thử nghiệm các chất ô nhiễm hữu cơ bền (POP) trong môi trường, chẳng hạn như dioxin, thuốc trừ sâu và hóa chất giống hormone, bằng phương pháp ELISA cạnh tranh (thử nghiệm hấp thụ miễn dịch liên kết enzyme), và kiểm tra nội độc tố của vi khuẩn gây tăng thân nhiệt ở người.
Việc xác định và khả năng áp dụng của giá trị tới hạn và giá trị tối thiểu phát hiện được của biến trạng thái tịnh được mô tả trong TCVN 10431-1 (ISO 11843-1) và TCVN 10431-2 (ISO 11843-2). Tiêu chuẩn này mở rộng các khái niệm trong TCVN 10431-2 (ISO 11843-2) cho trường hợp hiệu chuẩn phi tuyến.
Giá trị tới hạn, xc, và giá trị tối thiểu phát hiện được, xd, đều được cho theo đơn vị của biến trạng thái tịnh. Nếu xc và xd được xác định dựa trên phân bố cho biến đáp ứng thì việc xác định cần bao gồm hàm hiệu chuẩn để chuyển đổi biến đáp ứng sang biến trạng thái tịnh. Tiêu chuẩn này xác định xc và xd dựa trên phân bố cho biến trạng thái tịnh không phụ thuộc vào dạng hàm hiệu chuẩn. Kết quả là có được định nghĩa bất kể dạng của hàm này là tuyến tính hay phi tuyến.
Hàm hiệu chuẩn cần liên tục, phân biệt được và đơn điệu tăng hoặc giảm.
Một phương pháp nữa được mô tả cho trường hợp trong đó SD hoặc CV chỉ được biết trong vùng lân cận giá trị tối thiểu phát hiện được.
Các ví dụ cũng được đưa ra.
Các tài liệu viện dẫn trong tiêu chuẩn này rất cần thiết cho việc áp dụng tiêu chuẩn. Đối với các tài liệu có ghi năm công bố thì áp dụng bản được nêu. Đối với các tài liệu không ghi năm công bố thì áp dụng phiên bản mới nhất, bao gồm cả các sửa đổi.
TCVN 8244-1 (ISO 3534-1), Thống kê học - Từ vựng và ký hiệu - Phần 1: Thuật ngữ chung về thống kê và thuật ngữ dùng trong xác suất
TCVN 8244-2 (ISO 3534-2), Thống kê học - Từ vựng và ký hiệu - Phần 2: Thống kê ứng dụng
ISO 3534-3, Statistics - Vocabulary and symbols - Part 3: Design of experiments (Thống kê học - Từ vựng và ký hiệu - Phần 3: Thiết kế thực nghiệm)
TCVN 6910-1 (ISO 5725-1), Độ chính xác (độ đúng và độ chụm) của phương pháp đo và kết quả đo - Phần 1: Nguyên tắc và định nghĩa chung
TCVN 10431-1:2014 (ISO 11843-1:1997), Năng lực phát hiện - Phần 1: Thuật ngữ và định nghĩa
TCVN 10431-2:2014 (ISO 11843-2:2000), Năng lực phát hiện - Phần 2: Phương pháp luận trong trường hợp hiệu chuẩn tuyến tính
Tiêu chuẩn này áp dụng các thuật ngữ và định nghĩa trong TCVN 8244 (ISO 3534) (tất cả các phần), TCVN 6910-1 (ISO 5725-1), TCVN 10431-1 (ISO 11843-1), TCVN 10431-2 (ISO 11843-2) và các thuật ngữ, định nghĩa dưới đây.
3.1. Giá trị tới hạn của biến trạng thái tịnh (critical value of the net state variable)
xc
Giá trị của biến trạng thái tịnh, X, mà nếu vượt quá giá trị này, với một xác suất sai lầm đã cho, a, sẽ dẫn đến quyết định là hệ thống được quan trắc không nằm trong trạng thái cơ sở của nó.
[TCVN 10431-1 (ISO 11843-1), định nghĩa 2.10]
Xem Hình 1.
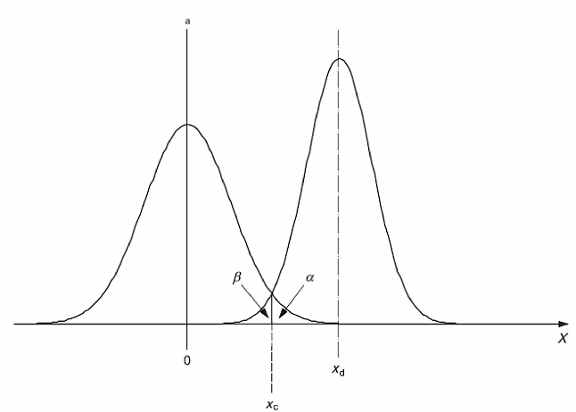
CHÚ DẪN
xc giá trị tới hạn của biến ở trạng thái tịnh
xd giá trị tối thiểu phát hiện được của biến trạng thái tịnh
X biến trạng thái tịnh
a xác suất sai lầm loại một ở X = 0
b xác suất sai lầm loại hai ở X = xd
a Mật độ xác suất.
CHÚ THÍCH: Hình 1 trong TCVN 10431-1:2014 (ISO 11843-1:1997) minh họa phân bố của biến đáp ứng và đường hiệu chuẩn phi tuyến. Hình 1 của tiêu chuẩn này minh họa phân bố của biến trạng thái tịnh được chuyển đổi qua độ dốc của đường hiệu chuẩn từ phân bố của biến đáp ứng thể hiện trong TCVN 10431-1 (ISO 11843-1).
Hình 1 - Phân bố của biến trạng thái tịnh ước lượng ở trạng thái cơ sở, X = 0 (bên trái) và ở trạng thái xd (bên phải)
3.2. Giá trị tối thiểu phát hiện được của biến trạng thái tịnh (minimum detectable value of the net state variable)
xd
Giá trị của biến trạng thái tịnh ở trạng thái thực tế, với xác suất (1 - b), sẽ dẫn đến kết luận là hệ thống không nằm trong trạng thái cơ sở của nó.
CHÚ THÍCH: Lấy từ TCVN 10431-1 (ISO 11843-1/Cor.1:2003), định nghĩa 2.11.
Xem Hình 1.
3.3. Độ chụm (precision)
CHÚ THÍCH 1: Hệ số biến động (CV) có thể được dùng như độ chụm thay cho SD khi thích hợp.
CHÚ THÍCH 2: Trong tiêu chuẩn này, độ chụm được xác định trong điều kiện lặp lại [TCVN 8244-2 (ISO 3534-2)].
CHÚ THÍCH 3: Các thuật ngữ, độ chụm và biên dạng độ chụm, được sử dụng trong tiêu chuẩn này, chứ không dùng không chụm và biên dạng không chụm, do các thuật ngữ này trước đây đã được sử dụng trong nhiều tình huống.
3.4. Biên dạng độ chụm (precision profile)
3.5. Biến đáp ứng (response variable)
Y
Biến thể hiện kết quả của thực nghiệm.
[ISO 3534-3:1999, định nghĩa 1.2]
CHÚ THÍCH 1: Với mục đích của bộ tiêu chuẩn này, định nghĩa chung này được hiểu theo dạng đặc biệt là: quan sát được trực tiếp thay thế cho biến trạng thái Z.
CHÚ THÍCH 2: Biến đáp ứng, Y, là biến ngẫu nhiên trong giai đoạn phân tích bất kỳ và nếu chuyển đổi bằng hàm hiệu chuẩn, biên dạng độ chụm của nó được biểu thị bằng độ lệch chuẩn và hệ số biến động, sX(X) và rX(X), tương ứng, của biến trạng thái tịnh.
3.6. Biên dạng độ chụm của biến đáp ứng (precision profile of response variable)
Đồ thị liên tục trong tiêu chuẩn này thu được trên cơ sở độ không đảm bảo của biến đáp ứng xuất phát từ tính chất ngẫu nhiên của các bước phân tích như dùng ống pipet và nhiễu đường nền thiết bị, chứ không phải từ sai số hệ thống thường được biết như là hiểu biết về sự không ổn định của thiết bị đo.
3.7. Biến trạng thái tịnh (net state variable)
X
Hiệu giữa biến trạng thái, Z, và giá trị của nó ở trạng thái cơ sở, z0.
[TCVN 10431-1 (ISO 11843-1), định nghĩa 2.4]
CHÚ THÍCH: Biến trạng thái tịnh, X, là biến tất định trong giai đoạn phân tích trong đó đường hiệu chuẩn được chuẩn bị và biên dạng độ chụm, biểu thị bằng sX(X) và rX(X), bắt nguồn từ tính ngẫu nhiên của biến đáp ứng.
4. Biên dạng độ chụm của biến đáp ứng
Vì lý do thực nghiệm hoặc lý thuyết, độ chụm (SD hoặc CV) liên quan đến biến đáp ứng, Y (chứ không phải biến trạng thái tịnh, X). Do đó, mọi giá trị liên quan của Y cần được chuyển đổi thành giá trị X tương ứng và độ chụm được chuyển đổi theo, như thể hiện trên Hình 2 [1, 2].

Hình 2 - Chuyển đổi độ không đảm bảo từ biến đáp ứng sang biến trạng thái tịnh
Trong Hình 3, SD, sY(X), của biến đáp ứng có thể chuyển đổi thành SD, sX(X), của biến trạng thái tịnh bằng cách lấy giá trị tuyệt đối đạo hàm, |dY/dX|, của hàm hiệu chuẩn: sX(X) = sY(X) /|dY/dX|. Phép chuyển đổi thành CV của X, rX(X), có thể lập thành công thức:
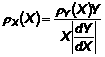 (1)
(1)
Cho rY(X) là hàm của X, đại lượng mong muốn, rX(X), cũng có thể viết thành hàm của X với sự hỗ trợ của Công thức (1). Việc sử dụng giá trị tuyệt đối, |dY/dX|, mở rộng ứng dụng tiêu chuẩn này cho các hàm hiệu chuẩn chỉ đơn điệu giảm.
CHÚ THÍCH 1: Nếu hàm hiệu chuẩn là đường thẳng đi qua gốc (Y = aX), biên dạng độ chụm, rX(X), của biến trạng thái tịnh bằng biên dạng độ chụm, rY(X), của biến đáp ứng. Chú ý là Y/X = |dY/dX| = a, khi Y = aX.
CHÚ THÍCH 2: Công thức (1) không hợp lệ đối với X = 0, nhưng bao trùm hầu hết các tình huống thực tế trong đó hệ số biến động rX(X), hướng đến vô cùng với X giảm chừng nào SD, sX(X) (=rY(X)Y/|dY/dX|), của biến trạng thái tịnh là hữu hạn.
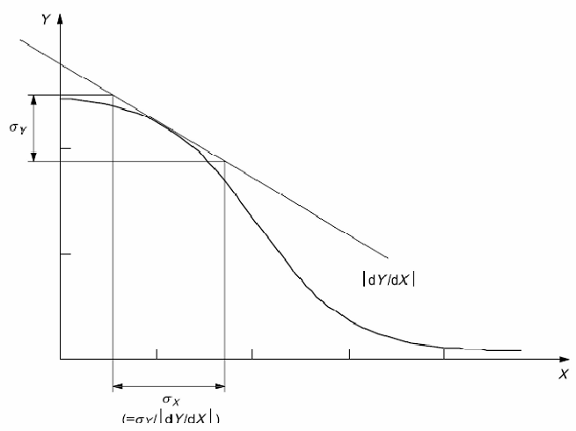
Hình 3 - Chuyển đổi từ SD, sY, của biến đáp ứng thành SD, sX, của biến trạng thái tịnh bằng cách lấy giá trị tuyệt đối đạo hàm, |dY/dX|, của đường cong hiệu chuẩn
5. Giá trị tới hạn và giá trị tối thiểu phát hiện được của biến trạng thái tịnh
5.1. Khái quát
Tất cả các xác định dưới đây đều dựa trên phân bố xác suất đối với biến trạng thái tịnh.
Giá trị tới hạn, xc, được xác định là:
xc = kcsX(0) (2)
trong đó
kc ký hiệu cho hệ số để quy định a;
sX(0) là SD ở X = 0.
Nếu sử dụng quan hệ sX(0) = sY(0)/|dY/dX|, Công thức (2) có thể mô tả là xc = kcsY(0)/|dY/dX|.
Giá trị tối thiểu phát hiện được, xd, được xác định là
xd = xc + kdsX(xd) (3)
trong đó
kd ký hiệu cho hệ số để quy định b;
sX(xd) là SD ở X = xd (xem Hình 1).
Biên dạng độ chụm sX(X), (xem 3.4) là cần thiết để xác định giá trị tới hạn, xc, và giá trị tối thiểu phát hiện được, xd.
CHÚ THÍCH 1: Nếu biến trạng thái tịnh có phân bố chuẩn, hệ số kc = kd = 1,65, thì quy định xác suất, a = b = 5 %.
CHÚ THÍCH 2: Với giả định đặc biệt rằng sX(X) là hằng số [sX(X) = sX] và kc = kd = 1,65, thì Công thức (2) và (3) có thể viết đơn giản thành xc = 1,65sX và xd = 3,30sX.
5.2. Tính toán liên quan đến xác suất a
Nếu có SD đối với X = 0 thì sX(0) được sử dụng thay cho sX(xd), định nghĩa xc và xd có dạng:
xc = kcsX(0) (4)
xd = (kc + kd)sX(0) (5)
Trong trường hợp này, Công thức (4) giống Công thức (2) và xác suất a bằng với định nghĩa chung.
Tuy nhiên, xác suất b có thể khác với b ban đầu. Không yêu cầu biên dạng độ chụm đầy đủ sX(X) đối với tính toán này.
CHÚ THÍCH: Với giả định đặc biệt rằng sX(X) là hằng số [sX(X) = sX] và kc = kd = 1,65, thì Công thức (4) và (5) có thể viết đơn giản thành xc = 1,65sX và xd = 3,30 sX.
5.3. Tính toán liên quan đến xác suất b
Khi sX(xd) được sử dụng thay cho sX(0) ở 5.2 thì định nghĩa xc và xd có dạng:
xc = kcsX(xd) (6)
xd = (kc + kd)sX(xd) (7)
Trong trường hợp này, xác suất b bằng với định nghĩa chung, nhưng xác suất a có thể khác với a ban đầu.
CHÚ THÍCH: Với giả định đặc biệt rằng sX(X) là hằng số [sX(X) = sX] và kc = kd = 1,65, thì Công thức (6) và (7) có thể viết đơn giản thành xc = 1,65sX và xd = 3,30sX.
5.4. Phương pháp vi phân
Định nghĩa ở 5.3 có một ưu điểm thực tế nếu biểu thị như Công thức (10). Công thức (7) có thể viết thành:
rX(xd) = sX(xd)/xd = 1/(kc + kd) (8)
Công thức này cho CV của biến trạng thái tịnh ở X = xd. Ưu điểm của Công thức (8) là giá trị tối thiểu phát hiện được, xd, có thể xác định như giá trị của biến trạng thái tịnh tại đó CV của biến trạng thái tịnh kỳ vọng là 1/(kc + kd) x 100 %. Biên dạng độ chụm liên tục, sX(X), là cần thiết đối với xd và xd.
Trong khi độ dốc, dY/dlgX, của đồ thị bán lôga (Y theo lg X) của hàm hiệu chuẩn thay đổi tùy thuộc vào biến trạng thái tịnh, X, thì độ dốc có giá trị cụ thể ở giá trị tối thiểu phát hiện được:
![]() (9)
(9)
trong đó vế trái thể hiện giá trị tuyệt đối của đạo hàm, |dY/dlgX|, tại X = xd (ln 10 = 2,303). Công thức này là quy tắc chung cho đường cong hiệu chuẩn và luôn đúng bất kể hình dạng của đường cong hiệu chuẩn (tuyến tính hay phi tuyến). Đạo hàm của công thức (9) được cho trong Phụ lục B.
CHÚ THÍCH 1: Nếu kc = kd = 1,65 thì công thức (8) có thể viết thành sX(X) = 1/3,30 = 30 %. xd nằm tại X, có CV là 30 %.
CHÚ THÍCH 2: Nếu kc = kd = 1,65 thì công thức (9) có thể viết thành
![]() (10)
(10)
trong đó hằng số 0,132 được xác định là 1/(3,3 x 2,303).
6.1. Khái quát
Điều 6.2 và 6.3 tập trung vào cách thức ước lượng biên dạng độ chụm (xem 3.4) được biểu thị theo SD hoặc CV của biến đáp ứng. Đại lượng cuối, rX(X), có thể được chuyển đổi từ đồ thị liên tục của SD hoặc CV của biến đáp ứng như trình bày trong Điều 4.
Ví dụ trong 6.4 thể hiện việc áp dụng phương pháp vi phân cho ELISA cạnh tranh. Trong 6.4, hàm hiệu chuẩn của ELISA cạnh tranh được chứng minh thường là phi tuyến, nhưng giả định về tính tuyến tính vẫn có hiệu lực ở các mức gần với giá trị tối thiểu phát hiện được.
6.2. Luật lan truyền độ không đảm bảo
ELISA cạnh tranh cho 17a-hydroxyprogesteron được lấy làm ví dụ. Quy trình thực nghiệm của hệ thống này được thể hiện trên Hình 4. Phép thử này được tiến hành trên vi đĩa có 96 giếng. Đường hiệu chuẩn được lập cho đĩa này và phân tích thực tế các mẫu được thực hiện trong các giếng khác trên chính đĩa đó. Ở đây, độ không đảm bảo nội tại đĩa được kiểm tra.
Độ không đảm bảo của ELISA cạnh tranh về cơ bản là từ phản ứng cạnh tranh giữa mẫu và kháng nguyên gắn nhãn. Biến đáp ứng, Y (ở đây là phép đo độ hấp thụ), tỷ lệ với kháng nguyên gắn nhãn kết hợp với kháng thể (kháng huyết thanh) trên bề mặt giếng trong vi đĩa [1]
![]()
trong đó
X ký hiệu cho lượng mẫu (biến trạng thái tịnh);
G là lượng kháng nguyên gắn nhãn;
B là lượng kháng thể.
Dựa trên việc ứng dụng luật lan truyền độ không đảm bảo [3] cho quy trình thử nghiệm, rút ra được CV bình phương, rY(X)2, của biến đáp ứng, Y: [1]
![]() (11)
(11)
trong đó
X ký hiệu cho lượng mẫu (biến trạng thái tịnh);
Y là phép đo hấp thụ (biến đáp ứng) và có thể thay bằng hàm hiệu chuẩn;
G là lượng kháng nguyên gắn nhãn (0,1 mg/l);
rX là CV của thể tích pipet của mẫu (0,9 %);
rG là CV của thể tích pipet của kháng nguyên gắn nhãn (0,9 %);
rB là CV của thể tích pipet của kháng huyết thanh (1,9 %);
rS là (2/3) x (CV của thể tích pipet của dung dịch nhiễm sắc -cơ chất), trong đó hệ số 2/3 được sử dụng để chuyển đổi sai số thể tích của pipet thành sai số cơ bản của sản phẩm nhiễm sắc xuất hiện trên bề mặt giếng trên vi đĩa (0,6 %);
sW là SD của phép đo hấp thụ trong các giếng của vi đĩa và là hằng số trong chừng mực liên quan đến độ không đảm bảo nội tại đĩa (độ hấp thụ 0,002).
Đại lượng cuối của độ chụm, rX(X), có thể được tính từ công thức (11) như thể hiện trên Hình 2.

Hình 4 - Quy trình thực nghiệm phương pháp ELISA cạnh tranh
Biên dạng độ chụm, rX(X), của ví dụ này được cho trên Hình 5. Hệ số CV, rX(X), được tính từ công thức (11) với tham số thực tế mô tả ở trên và được biểu thị bằng phần trăm. Nếu chấp nhận việc xác định ở 5.3 thì có thể xác định giá trị tối thiểu phát hiện được, xd, trên biên dạng độ chụm (xem mũi tên ở Hình 5). Ý nghĩa của 30 % CV được nêu trong Chú thích 1 của 5.4.
Biên dạng độ chụm trong thang đo chuẩn và thang đo bán lôga cho cùng một giá trị tối thiểu phát hiện được. Hình 5 b) loại trừ điểm X = 0 và cả CV trong đó. Tuy nhiên, điều này không gây ra vấn đề gì, về lý thuyết hay thực tế, vì yêu cầu của tiêu chuẩn này đối với giá trị tối thiểu phát hiện được là giá trị CV biểu thị bằng biên dạng độ chụm quanh giá trị tối thiểu phát hiện được.
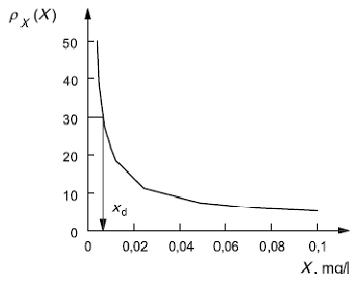
a) Thang đo thường

b) Đồ thị bán lôga
Hình 5 - CV của biến trạng thái tịnh, rX(X), (biên dạng độ chụm) và giá trị tối thiểu phát hiện được, xd, trên thang đo thường và đồ thị bán lôga đối với phương pháp ELISA cạnh tranh cho hydroxyprogesteron-17 a
6.3. Làm khớp mô hình
Trong phép thử miễn dịch, phương sai của biến đáp ứng có thể tính gần đúng bằng mô hình hàm mũ: [2]
sY(X)2 µ Yj (12)
trong đó sY(X) ký hiệu cho SD của biến đáp ứng, Y. Nếu j = 0, phương sai là hằng số. Nếu j = 1, phương sai tỷ lệ với biến đáp ứng. Nếu j = 2, hệ số CV, rY(X), của biến đáp ứng là hằng số. Hằng số tỷ lệ có thể xác định bằng phương pháp bình phương tối thiểu.
6.4. Áp dụng cho ELISA cạnh tranh
Trong ELISA cạnh tranh, đường cong hiệu chuẩn chuẩn hóa, gọi là B/B0, thường được sử dụng và công thức (10) có thể được viết là: [4]
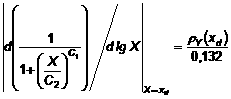 (13)
(13)
trong đó rY(xd) ký hiệu cho CV đáp ứng tại xd. Nguồn dẫn xuất được nêu trong Phụ lục C.
Giá trị tối thiểu phát hiện được của biến trạng thái tịnh có thể tìm được từ độ dốc xác định bởi công thức (13). Hình 6 thể hiện đường cong B/B0 bán lôga trong ELISA cạnh tranh đối với 17a- hydroxyprogesteron (giống như ví dụ 6.2). Nếu CV đáp ứng quan sát được là 1,9 % CV ở nồng độ mẫu thấp được sử dụng cho phép gần đúng [» rY(xd)], công thức (13) cho 0,15 (= 0,019 / 0,132).
Ước lượng bằng đồ thị của xd được thực hiện như sau (xem Hình 6):
- Bước 1: vẽ đường thẳng có độ dốc tính bằng công thức (13) với trợ giúp của thang đo ở góc dưới bên trái;
- Bước 2: vẽ đường tiếp tuyến chạm đường cong B/B0 với cùng độ dốc như trong bước 1;
- Bước 3: kẻ đường vuông góc từ điểm tiếp xúc tới trục X.
Điểm giao nhau của đường vuông góc và trục X ứng với xd. Phương pháp này cho kết quả gần như tương tự như ví dụ ở 6.2 (so sánh Hình 5 và Hình 6).
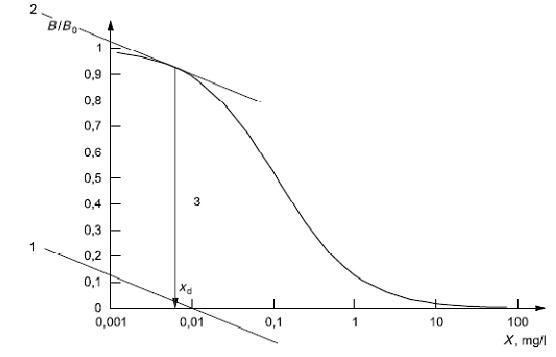
CHÚ DẪN
1, 2, 3 bước 1, 2 và 3 như mô tả trong 6.4.
Hình 6 - Đồ thị bán lôga của đường cong B/B0 trong phép thử ELISA cạnh tranh đối với 17a-hydroxyprogesteron
Ký hiệu và chữ viết tắt sử dụng trong tiêu chuẩn này
| SD | độ lệch chuẩn |
| CV | hệ số biến động (SD chia cho trung bình) |
| POP | chất gây ô nhiễm hữu cơ bền |
| ELISA | thử nghiệm hấp thụ miễn dịch liên kết enzyme |
| X | biến trạng thái tịnh |
| Y | biến đáp ứng |
| xc | giá trị tới hạn của biến trạng thái tịnh |
| xd | giá trị tối thiểu phát hiện được của biến trạng thái tịnh |
| kc | hệ số để quy định a |
| kd | hệ số để quy định b |
| a | xác suất sai lầm loại một tại X = 0 |
| b | xác suất sai lầm loại hai tại X = xd |
| sY(X) | SD của biến đáp ứng là hàm số của X |
| rY(X) | CV của biến đáp ứng là hàm số của X |
| sX(X) | SD của biến trạng thái tịnh là hàm số của X |
| rX(X) | CV của biến trạng thái tịnh là hàm số của X |
| |dY/dX| | đạo hàm của hàm hiệu chuẩn |
| B/B0 | tỷ số của phép đo liều tùy ý với phép đo liều bằng không |
Công thức biến đổi [công thức (1)] có thể dùng để thay đổi công thức xác định xd [công thức (7)] như trình bày dưới đây:
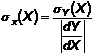
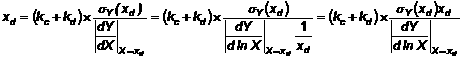
trong đó giá trị tuyệt đối của đạo hàm được sử dụng trong trường hợp độ dốc âm. Các biến chưa biết, xd, có thể loại khỏi công thức trên:
![]()
Việc chuyển đổi logarit tự nhiên thành logarit thập phân cho mục đích thực hành (ln X = 2,303 lg X) có thể dẫn đến công thức mục tiêu [công thức (9)]. Xem thêm Tài liệu tham khảo [4].
Trong phép thử ELISA so sánh, đường cong hiệu chuẩn thường được biểu thị như hàm logistic bốn tham số:
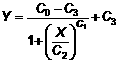
và dạng chuẩn của nó là B/B0:
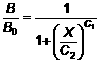
trong đó C0, C1, C2 và C3 là các hệ số cần xác định bằng phương pháp bình phương tối thiểu khớp với dữ liệu hiệu chuẩn thực tế. Thay thế quan hệ dY = (C0 - C3)d B/B0 vào công thức (10) ta có:
![]()
Vì hệ số C0 ký hiệu cho đáp ứng lớn nhất đối với mẫu trắng (X = 0) và C3 là đáp ứng nhỏ nhất ở nồng độ vô hạn (X = ¥), nên sY(X)/(C0 - C3) xấp xỉ bằng sY(X)/C0. Cho rY(X) được xác định là:
![]()
trong đó sY(X)/C0 nghĩa là CV của đáp ứng trắng, rY(0). Hai công thức cuối dẫn đến công thức (13).
Xem thêm Tài liệu viện dẫn [4].
THƯ MỤC TÀI LIỆU THAM KHẢO
[1] HAYASHI, Y., MATSUDA, R., MAITANI, T., IMAI, K., NISHIMURA, W., ITO, K., and MAEDA, M. Precision, limit of detection and range of quantitation in competitive ELISA. Anal. Chem., 76(5), 2004, pp. 1 295-1 301 (Độ chụm, giới hạn phát hiện và dãy định lượng trong ELISA cạnh tranh)
[2] DUDLEY, R.A., EDWARDS, P., EKINS, R.P., FINNEY, D.J., MCKENZIE, I.G.M., RAAB, G.,., RODBARD, D. and RODGERS, R.P.C. Guidelines for immunoassay data processing. Clin. Chem., 31(8), 1985, pp. 1 264-1 271 (Hướng dẫn xử lý dữ liệu xét nghiệm miễn dịch)
[3] Hướng dẫn trình bày độ không đảm bảo đo (GUM), BIPM, IEC, IFCC, ISO, IUPAC, IUPAP, OIML, 1993 1
[4] HAYASHI, Y., MATSUDA, R., ITO, K., IMAI, K., NISHIMURA, W., and MAEDA, M. Detection limit estimated from slope of calibration curve: An application to competitive ELISA. Anal. Sci., 21, 2005, pp. 167-169 (Giới hạn phát hiện ước lượng từ đường cong hiệu chuẩn: Ứng dụng ELISA cạnh tranh)
[5] ISO 3534-3:1999, Statistics - Vocabulary and symbols - Part 3: Design of experiments (Thống kê học - Từ vựng và ký hiệu - Phần 3: Thiết kế thực nghiệm)
MỤC LỤC
1. Phạm vi áp dụng
2. Tài liệu viện dẫn
3. Thuật ngữ và định nghĩa
4. Biên dạng độ chụm của biến đáp ứng
5. Giá trị tới hạn và giá trị tối thiểu phát hiện được của biến trạng thái tịnh
5.1. Khái quát
5.2. Tính toán liên quan đến xác suất a
5.3. Tính toán liên quan đến xác suất b
5.4. Phương pháp vi phân
6. Ví dụ
6.1. Khái quát
6.2. Luật lan truyền độ không đảm bảo
6.3. Làm khớp mô hình
6.4. Áp dụng cho ELISA cạnh tranh
Phụ lục A (quy định) Ký hiệu và chữ viết tắt sử dụng trong tiêu chuẩn này
Phụ lục B (tham khảo) Dẫn xuất công thức (9)
Phụ lục C (tham khảo) Dẫn xuất công thức (13)
Thư mục tài liệu tham khảo

