ISO/IEC 14888-3:2016
Information technology - Security techniques - Digital signatures with appendix - Part 3: Discrete logarithm based mechanisms
MỤC LỤC
Lời nói đầu
1 Phạm vi áp dụng
2 Tài liệu viện dẫn
3 Các thuật ngữ và định nghĩa
4 Các ký hiệu và chữ viết tắt
5 Mô hình tổng quát
5.1 Tiến trình tạo tham số
5.2 Tiến trình ký
5.3 Tiến trình kiểm tra
6 Các cơ chế dựa trên chứng thư số
6.1 Tổng quan
6.2 DSA
6.3 KCDSA
6.4 Thuật toán Pointcheval/Vaudenay
6.5. SDSA
6.6 EC-DSA
6.7 EC-KCDSA
6.8 EC-GDSA
6.9 EC-RDSA
6.10 EC-SDSA
6.11 EC-FSDSA
7 Các cơ chế dựa trên định danh
7.1 Tổng quan
7.2 IBS-1
7.3 IBS-2
Phụ lục A (Quy định) Định danh đối tượng
Phụ lục B (Quy định) Các hàm biến đổi (I)
Phụ lục C (Tham khảo) Các hàm biến đổi (lI)
Phụ lục D (Quy định) Sinh các tham số miền DSA
Phụ lục E (Tham khảo) Các cặp Weil và Tate
Phụ lục F (Tham khảo) Các ví dụ số
Phụ lục G (Tham khảo) So sánh các lược đồ chữ ký
Phụ lục H (Tham khảo) Các yêu cầu đặc điểm cho việc lựa chọn một cơ chế
Thư mục tài liệu tham khảo
Lời nói đầu
TCVN 12214-3 : 2018 hoàn toàn tương đương với ISO/IEC 14888-3:2016.
TCVN 12214-3 : 2018 do Cục Quản lý mật mã dân sự và Kiểm định sản phẩm mật mã biên soạn, Ban Cơ yếu Chính phủ đề nghị, Tổng cục Tiêu chuẩn Đo lường Chất lượng thẩm định, Bộ Khoa học và Công nghệ công bố.
Bộ tiêu chuẩn TCVN 12214 (ISO/IEC 14888) Công nghệ thông tin - Các kỹ thuật an toàn - Chữ ký số kèm phụ lục gồm các tiêu chuẩn sau:
- TCVN 12214-1 : 2018 (ISO/IEC 14888-1:2008) Phần 1: Tổng quan
- TCVN 12214-2 : 2018 (ISO/IEC 14888-2:2008) Phần 2: Các cơ chế dựa trên phân tích số nguyên
- TCVN 12214-3 : 2018 (ISO/IEC 14888-3:2016) Phần 3: Các cơ chế dựa trên logarit rời rạc
CÔNG NGHỆ THÔNG TIN - CÁC KỸ THUẬT AN TOÀN - CHỮ KÝ SỐ KÈM PHỤ LỤC - PHẦN 3: CÁC CƠ CHẾ DỰA TRÊN LOGARIT RỜI RẠC
Information technology - Security techniques - Digital signatures with appendix - Part 3: Discrete logarithm based mechanisms
Tiêu chuẩn này quy định các cơ chế chữ ký số kèm phụ lục, mà độ an toàn của nó dựa trên bài toán logarit rời rạc.
Tiêu chuẩn này cung cấp:
- Một sự mô tả chung của sơ đồ chữ ký số kèm phụ lục
- Một loạt các cơ chế cung cấp chữ ký số kèm phụ lục.
Với mỗi cơ chế, tiêu chuẩn này mô tả:
- Tiến trình sinh cặp khóa,
- Tiến trình tạo chữ ký,
- Tiến trình kiểm tra chữ ký.
Các tài liệu dưới đây, toàn bộ hoặc một phần, được tham chiếu trong tài liệu này rất cần thiết cho các ứng dụng của nó. Đối với các tài liệu viện dẫn ghi năm công bố, chỉ áp dụng các bản được nêu. Đối với các tài liệu viện dẫn không ghi năm công bố, thì bản tham chiếu cuối cùng được áp dụng.
TCVN 11816-3 (ISO/IEC 10118-3), Công nghệ thông tin - Các kỹ thuật an toàn - Hàm băm
TCVN 12214-1 (ISO/IEC 14888-1), Công nghệ thông tin - Các kỹ thuật an toàn - Chữ ký số kèm phụ lục - Phần 1: Tổng quan
Với mục đích của tài liệu này, các thuật ngữ và định nghĩa dưới đây được áp dụng.
3.1
Nhóm giao hoán hữu hạn (finite commutative group)
Tập hợp hữu hạn E với phép toán nhị phân “*” sao cho:
- Với mọi phần tử nhóm a, b ϵ E, a * b ϵ E;
- Với mọi phần tử nhóm a, b, c ϵ E, (a * b) * c = a * (b * c);
- Tồn tại một phần tử nhóm e ϵ E với e * a = a với mọi phần tử a ϵ E, với e được gọi là phần tử đơn vị của nhóm;
- Với mọi phần tử nhóm a ϵ E, tồn tại một phần tử nhóm b ϵ E sao cho b * a = e;
- Với mọi phần tử nhóm a, b ϵ E, a * b = b * a.
CHÚ THÍCH 1 Trong một vài trường hợp, khi E là tập các điểm trên một đường cong elliptic, phép toán số học trong tập hợp hữu hạn E được mô tả với ký hiệu cộng.
3.2
Nhóm cyclic (cyclic group)
Nhóm giao hoán hữu hạn (3.1) E của n phần tử chứa một phần tử nhóm a ϵ E, được gọi là phần tử sinh có bậc n.
3.3
Nhóm đường cong elliptic (elliptic curve group)
Nhóm cyclic (3.2) được định nghĩa trên các điểm của một đường cong elliptic trên trường hữu hạn.
CHÚ THÍCH 1 Giả sử F = GF(r) là ký hiệu của trường Galois với lực lượng r, với r hoặc là số nguyên tố lẻ p, hoặc r = 2m, với một số m nguyên dương.
Một đường cong elliptic được định nghĩa trên F có thể được xác định bởi công thức đường cong affine, hoặc là y2 = x3 + a1x + a2 (với r = p, p là một số nguyên tố lẻ) hoặc công thức y2 + xy = x3 + a1x2 + a2 (khi r = 2m, với m là số nguyên dương), với a1 và a2 là các phần tử của F. Đường cong elliptic E tương ứng bao gồm tập hợp các điểm affine F x F cùng với một điểm đặc biệt (không affine) điểm “vô cực”.
Một điểm affine P của E có thể được biểu diễn là một cặp thứ tự (Px, Py) ϵ F x F, sao cho sự lựa chọn x = Px và y = Py thỏa mãn công thức của đường cong affine đã cho và khi các phép toán số học được thực hiện trên trường F.
Giả sử “+” là ký hiệu của phép toán hai ngôi là phép toán cộng trên “đường cong elliptic”, được xác định cho các điểm affine của E theo quy tắc cát tuyến - tiếp tuyến. Khi, tập hợp các điểm affine của E được tăng lên bài 0E, một điểm đặc biệt của E “ở vô cực” đóng vai trò như là yếu tố đối với phép “+” (nhưng nó không được biểu diễn như một cặp trong tọa độ), tập hợp E cùng với phép “+” tạo thành một nhóm hữu hạn, giao hoán, nhóm đường cong elliptic, E.
CHÚ THÍCH 2 Lực lượng của nhóm đường cong E, nhiều hơn một số với số lượng cặp thứ tự trong F x F thỏa mãn công thức đường cong affine với E.
3.4
Bậc (của một phần tử nhóm a) (order (of a group element a)
Số nguyên dương n nhỏ nhất sao cho an = e, với e là phần tử đơn vị của nhóm, an được định nghĩa truy hồi sao cho a0 = e và an = a * am-1 (m > 0) , và * là phép toán nhóm.
3.5
Cặp (pairing)
Hàm số lấy hai phần tử P và Q từ nhóm đường cong elliptic (3.3) trên trường hữu hạn G1 như là đầu vào, và sinh ra một phần tử từ nhóm cyclic khác (3.2) trên trường hữu hạn G2 như là đầu ra, và nó có hai tính chất sau đây (ở đó nó được giả thiết rằng G1 và G2 có bậc là q, với q là số nguyên tố, và hai phần tử bất kỳ P, Q, đầu ra của hàm cặp được viết là
- Tính song tuyến: Nếu P, P1, P2, Q, Q1, Q2 là các phần tử của G1, và a là một số nguyên thỏa mãn 1 ≤ a ≤ q - 1, thì:
< P1 + P2, Q > = < P1, Q >*< P2, Q >,
< P, Q1 + Q2 > = < P, Q1 >*< P, Q2 >,
< [a]P, Q > = < P,[a]Q > = < P, Q > a ,
- Tính không suy biến: Nếu P là một phần tử không định danh của G1, < P, P > ≠ 1
3.6
Trung tâm sinh khóa tin cậy KGC (trusted key generation centre)
Bên thứ ba tin cậy, một cơ chế chữ kí số dựa trên định danh, sinh ra một khóa riêng cho mỗi người ký.
|
| Phép toán XOR được thực hiện trên từng bit của a và b, với a và b là các bit hoặc xâu bit cùng độ dài. |
| a1, a2 | Các hệ số của đường cong elliptic |
| a mod n | Cho một số nguyên a và một số nguyên dương n, số dư nguyên duy nhất r, 0 ≤ r ≤ (n - 1), thỏa mãn r = a - bn, với b là một số nguyên nào đó. |
| (A, B, C) | Các hệ số của công thức chữ ký số, cơ chế được đặc tả trong Điều 6, xác định cách chữ ký được tính toán. |
|
| CHÚ THÍCH 1 Công thức chữ ký số được đặc tả trong điều 5.2.1. |
|
| Một tham số được đặc tả trong mối quan hệ giữa khóa tạo chữ ký và khóa kiểm tra |
| E | Một đường cong elliptic được xác định bởi hai hệ số a1 và a2 |
| E | Một nhóm giao hoán hữu hạn; với các cơ chế dựa trên nhóm nhân, các phần tử của E trong |
| #E | Lực lượng của E; với các cơ chế dựa trên nhóm nhân |
| F | Một trường hữu hạn |
| Fp | một trường hữu hạn cấp p |
| gcd(N1, N2) | Ước số chung lớn nhất của các số nguyên N1 và N2. |
| G | Một phần tử có bậc q trong E |
| GF(r) | Trường hữu hạn với lực lượng r, với r là lũy thừa của số nguyên tố |
| G1 | Một nhóm cyclic bậc nguyên tố q; các phần tử của G1 là các điểm trên đường cong elliptic trên GF(r) |
| G2 | Một nhóm cyclic bậc nguyên tố q; các phần tử của G2 là các phần tử của một trường hữu hạn GF(r) |
| H1 | Một hàm băm chuyển đổi một xâu dữ liệu vào một phần tử trong G1 |
|
| CHÚ THÍCH 2 Xâu dữ liệu đầu vào được biến đổi thành số nguyên, sau đó số nguyên được chuyển thành một điểm của E trên GF(r) bằng cách sử dụng hàm I2P, được đặc tả trong Phụ lục C. |
| h, H2 | Các hàm băm, nghĩa là một trong các cơ chế được đặc tả trong TCVN 11816:2017 (ISO IEC 10118). |
| ID | Một xâu dữ liệu chứa một định danh của người ký, được dùng trong cơ chế IBS-1 và IBS-2 |
| m | Một bậc nhúng (hoặc bậc mở rộng) |
| [n]P | Phép toán nhân lấy đầu vào là một số nguyên dương n và một điểm P trên đường cong E và đưa ra đầu ra một điểm Q trên đường cong E, với Q = [n]P - P + P + … + P , cộng n-1 lần. Phép toán thỏa mãn tính chất [0]P = 0E (điểm vô cực), và [-n]P = [n](-P) |
| P | Phần tử sinh của G1 được dùng trong các cơ chế IBS-1 và IBS-2 |
| p | Một số nguyên tố hoặc lũy thừa của một số nguyên tố |
| q | Một số nguyên tố là ước của #E và bậc của G1 và G2 |
| r | Kích thước của GF(r); trong các cơ chế dựa trên nhóm cộng các điểm của đường cong elliptic, r là lũy thừa của số nguyên tố, pm, một vài số nguyên tố p ≥ 2 và số nguyên m ≥ 1. |
| T | Nhiệm vụ |
| T1 | Phần đầu tiên của nhiệm vụ T |
| T2 | Phần thứ hai của nhiệm vụ T |
| U | Khóa chủ riêng của KGC, được tạo ra từ việc lựa chọn một số nguyên ngẫu nhiên, được dùng trong các cơ chế IBS-1 và IBS-2 |
| V | Khóa chủ công khai của KGC, một phần tử của G1, được dùng trong các cơ chế IBS-1 và IBS-2 |
|
| Tập hợp các số nguyên i với 0 < i < N và gcd(i, N) = 1 với các phép toán số học được định nghĩa theo modulo N. |
|
| Tập hợp các số nguyên i với 0 < i < p và p là một số nguyên tố, nhóm này là một nhóm nhân. |
| α | Độ dài của số nguyên tố (hoặc lũy thừa của số nguyên tố) p theo bit. |
| β | Độ dài của số nguyên tố q theo bit |
| γ | Độ dài đầu ra của hàm băm h và H2 theo bit |
| Π | Tiền chữ ký |
| ΠX | Tọa độ x của Π trong đó Π = (ΠX, ΠY) là một điểm của đường cong elliptic |
| ΠY | Tọa độ y của Π trong đó Π = (ΠX, ΠY) là một điểm của đường cong elliptic |
| Πa | Phân tử đầu tiên của Π trong đó Π = (Πa, Πb) là một phần tử của trường mở rộng bậc 2. |
| Πb | Phần tử thứ hai của Π trong đó Π = (Πa, Πb) là một phần tử của trường mở rộng bậc 2. |
| 0E | Điểm ở vô cực trên đường cong elliptic E |
| <> | Một cặp song tuyến và không suy biến |
| || | X||Y được dùng với nghĩa của kết quả phép ghép dữ liệu của X và Y theo trật tự được đặc tả |
5.1.1 Các cơ chế dựa trên chứng thư
5.1.1.1 Sinh các tham số miền
Đối với các cơ chế chữ ký số dựa trên logarit rời rạc, tập hợp các tham số miền bao gồm các tham số sau:
- E một nhóm giao hoán hữu hạn;
- q, một ước nguyên tố của #E;
- G, một phần tử bậc q trong E.
Trong nhóm E, ký hiệu nhân được sử dụng, cần lưu ý rằng, với một cơ chế ký cụ thể được lựa chọn có thể cần thêm một số ràng buộc trong việc lựa chọn E, q, G.
5.1.1.2 Tạo chữ ký và kiểm tra chữ ký
Khóa ký X của một chủ thể được sinh ra một cách bí mật ngẫu nhiên hoặc giả ngẫu nhiên sao cho 0 < X < q. Khóa công khai kiểm tra tương ứng Y là một phần tử của E và được tính như sau:
![]()
Với D là một tham số được xác định bởi cơ chế được dùng. Giá trị của D là một trong hai giá trị -1 và 1.
CHÚ THÍCH Một cài đặt vẫn được xem là phù hợp nếu loại trừ một vài số nguyên từ việc xem xét các giá trị X. Ví dụ, giá trị 1 có thể bị loại trừ vì giá trị này dẫn đến khóa kiểm tra của người dùng là phần tử sinh G, nó được dễ dàng phát hiện.
5.1.2 Các cơ chế dựa trên định danh
5.1.2.1 Ký hiệu
Hai cơ chế dựa trên định danh được đặc tả trong Điều 7 đều dựa trên việc sử dụng các cặp trên các nhóm đường cong elliptic. Để đặc tả cơ chế dựa trên định danh, ký hiệu nhóm cộng được sử dụng.
5.1.2.2 Sinh các tham số miền
Tập hợp các tham số miền bao gồm các tham số sau:
- E, một nhóm giao hoán hữu hạn;
- GF(r), trường Galois lực lượng r;
- G1, một nhóm cyclic bậc nguyên tố q
- G2, một nhóm cyclic bậc nguyên tố q
- P, một phần tử sinh của G1;
- q, là một số nguyên tố, lực lượng của G1, G2.
- <>, một cặp song tuyến và không suy biến.
5.1.2.3 Sinh khóa chủ
Một khóa chủ riêng của KGC là một khóa ngẫu nhiên bí mật hoặc số giả ngẫu nhiên U sao cho 0 < U < q. Khóa chủ công khai V là một phần tử của G1 và được tính như sau: V = [U]P.
5.1.2.4 Sinh khóa chữ ký và khóa kiểm tra
Một khóa ký của chủ thể ký là một phần tử của G1 và được tính bởi KGC như sau X = [U]Y.
Với U là khóa riêng của KGC và Y = H1(ID) là khóa kiểm tra công khai, với ID là một xâu định danh cho KGC và hàm băm H1.
5.1.3 Lựa chọn tham số
5.1.3.1 Kích thước tham số lựa chọn
Độ dài bit của các tham số cho mức an toàn tiêu biểu được chỉ ra trong Bảng 1. Mức an toàn tối thiểu được đề xuất là 2112.
CHÚ THÍCH 1 Mức an toàn có nghĩa là số lượng bước trong tấn công tốt nhất đã biết lên mật mã nguyên thủy. Nếu 2112 bước được yêu cầu trong tấn công tốt nhất lên một hàm băm, thì độ an toàn của hàm băm này là 2112. Để bổ sung các phân tích kích thước tham số, xem tài liệu số [25] và [34].
Không cần thiết phải chọn α, β và γ có độ an toàn như nhau; mức độ an toàn của một lần thực hiện lược đồ chữ ký là nhỏ nhất của mức độ an toàn của các tham số.
Bảng 1 - Kích thước các tham số tuân theo mức an toàn
| Mức độ an toàn | 280 | 2112 | 2128 | 2192 | 2256 |
| α | 1024 | 2048 | 3072 | 7680 | 15360 |
| β | 160 | 224 | 256 | 384 | 512 |
| γ | 160 | 224 | 256 | 384 | 512 |
Được khuyến nghị mức an toàn là 280 nên sử dụng đối với các ứng dụng kế thừa.
CHÚ THÍCH 2 Không phải mọi cơ chế được đặc tả trong tiêu chuẩn này cung cấp tất cả các mức an toàn được mô tả trong bảng. Với ví dụ là DSA trong 6.1 chỉ cung cấp độ an toàn đến 2128.
5.1.3.2 Lựa chọn một hàm băm
Việc lựa chọn một hàm băm cần dựa vào tiêu chuẩn TCVN 11816-3 (ISO/IEC 10118-3). Nghĩa là h và H2 sẽ là một trong các cơ chế được đặc tả trong TCVN 11816-3 (ISO/IEC 10118-3), và H1 biến đổi một xâu bit thu được bởi một trong các cơ chế được đặc tả trong TCVN 11816-3 (ISO/IEC 10118-3) vào một phần tử trong G1.
Các hàm băm được dùng trong tiêu chuẩn này nên là hàm băm kháng va chạm.
Độ dài an toàn của hàm băm được lựa chọn nên trùng hoặc vượt quá độ dài an toàn của các tham số được dùng trong tạo khóa. Mối quan hệ giữa độ dài an toàn của hàm băm và các tham số tạo khóa được chỉ ra trong 5.1.3.1.
Hơn nữa, việc triển khai kiểm tra chữ ký số phải có cách xác định an toàn mà hàm băm nào được dùng bởi người ký. Nếu không, kẻ tấn công có thể truy vấn người kiểm tra dùng một hàm băm khác yếu hơn, và vì vậy bỏ qua mức an toàn dự định.
5.1.4 Tính đúng đắn của các tham số miền và khóa kiểm tra
Người kiểm tra chữ ký có thể yêu cầu đảm bảo các tham số miền và các khóa công khai kiểm tra là hợp lệ nếu không sẽ không có đảm bảo việc thỏa mãn các yêu cầu an toàn dự kiến ngay cả khi chữ ký số đã được kiểm tra và đối phương cũng có thể sinh các chữ ký đã kiểm tra.
Việc đảm bảo tính đúng đắn của các tham số miền có thể được cung cấp theo các cách sau:
- Việc lựa chọn các tham số miền hợp lệ từ một nguồn công khai tin cậy, như là chuẩn;
- Việc sinh các tham số hợp lệ bởi bên thứ ba tin cậy, như CA hoặc KGC;
- Tính hợp lệ của lực lượng tham số miền được sinh bởi bên thứ ba tin cậy, như CA hoặc KGC;
- Đối với người ký, việc tạo các tham số miền hợp lệ bằng cách sử dụng một hệ thống tin cậy;
- Tính hợp lệ của các tham số miền bởi người dùng (nghĩa là người ký hoặc người kiểm tra).
Việc đảm bảo tính hợp lệ của khóa kiểm tra công khai, có thể được cung cấp bởi một trong các điều sau đây:
- Với người ký, việc tạo ra cặp khóa ký riêng/khóa kiểm tra công khai dùng một hệ thống tin cậy;
- Với người ký hoặc người kiểm tra, tính hợp lệ của khóa kiểm tra công khai bởi bên thứ ba tin cậy, như CA hoặc KGC;
- Tính hợp lệ của việc kiểm tra khóa công khai bởi người dùng (hoặc là người ký hoặc là người kiểm tra).
CHÚ THÍCH 1 Tính hợp lệ của các tham số miền và khóa được yêu cầu. Tuy nhiên, cách để đạt được nằm ngoài phạm vi của tiêu chuẩn này.
CHÚ THÍCH 2 Phương pháp xác thực người ký là độc lập trên ứng dụng thực tế, cũng nằm ngoài phạm vi của tiêu chuẩn này.
5.2.1 Tổng quan
Tất cả các cơ chế chữ ký trong tiêu chuẩn này đều sử dụng một giá trị ngẫu nhiên K, mà được dùng (cùng với thông điệp) để tạo ra bằng chứng R (phần đầu tiên của chữ ký) và một nhiệm vụ (T1, T2). Chữ ký cho thông điệp là cặp (R, S) với S (là thành phần thứ hai của chữ ký) được tính bởi các giải pháp của công thức chữ ký.
Trong các cơ chế dựa trên chứng thư số, được đặc tả trong Điều 6, công thức chữ ký là:
AK + BXD + C ≡ 0(mod q),
(A, B, C) đã cho là một chuyển vị của (S, T1, T2), X là một khóa riêng và D là một tham số phụ thuộc vào cơ chế cụ thể.
Trong các cơ chế dựa trên định danh đặc tả ở Điều 7, công thức chữ ký là:
[K]A + [UD]B + C ≡ 0E (trong G1)
(A, B, C) đã cho là một chuyển vị của (S,T1,T2), U là chủ khóa riêng và D là một tham số phụ thuộc vào cơ chế cụ thể.
Việc chuyển vị sẽ được xác định hoặc được thỏa thuận khi cài đặt hệ thống chữ ký số.
Tiến trình tạo chữ ký và định dạng của thông điệp đã ký bao gồm 8 bước (xem Hình 1):
- Sinh số ngẫu nhiên;
- Tạo ra tiền chữ ký;
- Chuẩn bị thông điệp để ký;
- Tính toán bằng chứng;
- Tính toán nhiệm vụ (không cần thiết tính toán nhiệm vụ trong các cơ chế dựa trên định danh);
- Tính toán phần thứ hai của chữ ký;
- Xây dựng phụ lục;
- Xây dựng thông điệp đã ký.
Trong tiến trình này, chủ thể ký đều sử dụng khóa ký riêng, khóa kiểm tra công khai (lựa chọn) và các tham số miền.
5.2.2 Sinh số ngẫu nhiên
Với mỗi lần ký, chủ thể sinh mới một giá trị ngẫu nhiên bí mật là một số nguyên K với 0 < K < q. Đầu ra của bước này là K, nó sẽ được giữ bí mật và tiêu hủy an toàn sau khi dùng.
CHÚ THÍCH 1 Số ngẫu nhiên K có thể được xem xét như khóa dùng 1 lần.
CHÚ THÍCH 2 Với lý do hợp lý 5.1.1.2 việc thực thi vẫn được xem xét phù hợp, nếu loại trừ một vài số nguyên từ sự xem xét giá trị K có thể.
5.2.3 Tạo ra tiền chữ ký
Đầu vào của bước này là số ngẫu nhiên K và khóa chữ ký lựa chọn X, với chủ thể ký được tính là tiền chữ ký, Π, nhờ dùng K và tham số công khai làm đầu vào. Trong các cơ chế dựa trên chứng thư số được đặc tả trong Điều 6, nó được tính như sau:
Π = GK thuộc E.
Trong các cơ chế dựa trên định danh được đặc tả trong Điều 7, nó được đặc tả một cách riêng rẽ trong các cơ chế. Đầu ra của bước này là tiền chữ ký Π.
5.2.4 Chuẩn bị thông điệp để ký
Trong các tiến trình chuẩn bị, một trong các thông điệp M1 và M2 trở thành thông điệp M, các trường hợp khác là rỗng.
5.2.5 Tính toán các bằng chứng (phần đầu tiên của chữ ký)
Các biến đến bước này là tiền chữ ký Π từ 5.2.3 và M1 từ 5.2.4. Các giá trị của các biến được lựa chọn như đầu vào của hàm bằng chứng. Đầu ra của hàm bằng chứng là chứng cứ R. Hàm bằng chứng được đặc tả trong các cơ chế.
5.2.6 Tính toán các nhiệm vụ
Các đầu vào hàm nhiệm vụ là phần thứ nhất của chữ ký, với bằng chứng R từ 5.2.5, M2 từ 5.2.4 và điều kiện khóa kiểm tra Y. Các đầu ra của hàm nhiệm vụ là nhiệm vụ T = (T1, T2). Trong các cơ chế dựa trên chứng thư số được đặc tả trong Điều 6, T1 và T2 là các số nguyên như sau:
0 < |T1| < q, 0 < |T2| < q
Trong các cơ chế dựa trên định danh được đặc tả trong Điều 7, T1 và T2 là các phần tử của G1. Nó không cần thiết để tính T trong các cơ chế dựa trên định danh.
5.2.7 Tính toán phần thứ hai của chữ ký
Các đầu vào của bước này là số ngẫu nhiên K từ 5.2.1, khóa chữ ký X, nhiệm vụ T = (T1, T2) từ 5.2.6 chuyển vị (A, B, C) của (S,T1,T2), một biến D trong 5.1.12 và tham số miền q như được đặc tả trong 5.1.1.1 và 5.1.2.1.
Trong các cơ chế dựa trên chứng thư số, công thức ký là:
AK + BXD + C ≡ 0(mod q)
Và tính công thức chữ ký cho S, các phần thứ hai của chữ ký, với 0 < S < q.
Các cơ chế dựa trên định danh, các chủ thể ký tính toán công thức chữ ký cho S, phần thứ hai của chữ ký S ϵ G1. Giải pháp này thỏa mãn công thức chữ ký:
[K]A + [UD]B + C ≡ 0E (thuộc G1)
Cặp (R, S) sẽ được gọi là chữ ký, Σ.
5.2.8. Xây dựng phần phụ lục
Phụ lục được xây dựng từ chữ ký và một trường text tùy chọn, text, như là [(R,S), text]. Trường text có thể bao gồm một chứng thư số mà mật mã ràng buộc khóa kiểm tra công khai với dữ liệu định danh của chủ thể ký
Như được chỉ ra trong TCVN 12214-1 (ISO/IEC 14888-1), tùy thuộc vào các ứng dụng, có các phương án khác nhau của việc tạo ra phần phụ lục và để bổ sung cho thông điệp. Yêu cầu chung đối với người kiểm tra có thể có liên quan đến chữ ký số đúng cho thông điệp. Để kiểm tra thành công, cần thiết quá trình tiền kiểm tra, người kiểm tra có thể liên kết khóa kiểm tra đúng với chữ ký.
5.2.9. Xây dựng thông điệp đã ký
Thông điệp đã ký nhận được bằng cách ghép thông điệp M và phần phụ lục, nghĩa là, M||[(R,S),text].
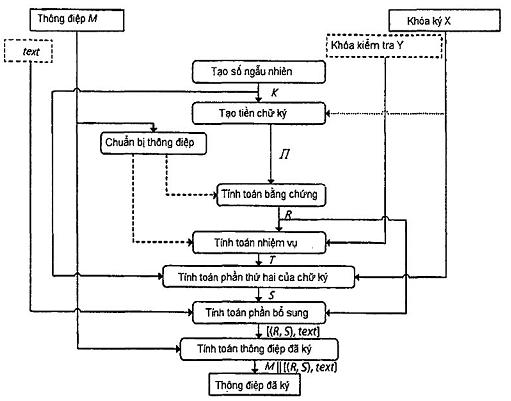
Hình 1 - Tiến trình chữ ký với bằng chứng ngẫu nhiên (một trong số M1 và M2 là M, trường hợp còn lại là rỗng)
5.3.1 Tổng quan
Quá trình kiểm tra bao gồm 6 bước sau (xem Hình 2) :
- Truy xuất bằng chứng;
- Chuẩn bị thông điệp để kiểm tra;
- Truy xuất các nhiệm vụ (là lựa chọn để tính nhiệm vụ trong các cơ chế dựa trên định danh);
- Tính lại tiền chữ ký;
- Tính lại các bằng chứng;
- Kiểm tra các bằng chứng.
Trong tiến trình này, người kiểm tra dùng khóa kiểm tra của người ký, khóa chủ công khai của KGC (chỉ dành cho các cơ chế dựa trên định danh mô tả ở mục 7) và các tham số miền.
5.3.2 Truy xuất các bằng chứng
Người kiểm tra truy xuất chữ ký số (R,S) từ phần phụ lục, và chia cho bằng chứng R và phần thứ hai của chữ ký S. Cũng vậy, người kiểm tra kiểm tra khoảng và độ dài bit của các phần tử chữ ký, R, S, theo các quy luật được đặc tả bởi mỗi tiến trình ký. Nếu luật định nghĩa trước bị vi phạm, chữ ký sẽ bị từ chối.
5.3.3 Chuẩn bị thông điệp để kiểm tra
Người kiểm tra truy xuất M từ thông điệp đã ký và chia thông điệp thành hai phần M1, M2.
5.3.4 Truy xuất nhiệm vụ
Bước này giống với 5.2.6. Các đầu vào cho hàm nhiệm vụ bao gồm bằng chứng R từ 5.3.2, M2 từ Điều 5.3.3, và (được lựa chọn) khóa kiểm tra Y. Nhiệm vụ T = (T1, T2) được tính lại như là đầu ra từ hàm nhiệm vụ. Trong các cơ chế dựa trên định danh, không cần thiết phải tính lại T.
5.3.5 Tính lại tiền chữ ký
Các đầu vào cho bước này là tập hợp của các tham số miền, khóa kiểm tra Y, nhiệm vụ T = (T1, T2) từ 5.3.4, phần thứ 2 của chữ ký S từ 5.3.2, và lựa chọn R từ 5.3.2. Người kiểm tra chỉ định các hệ số (A, B, C) các giá trị (S, T1, T2) theo trật tự được chỉ định bởi hàm chữ ký, và trong các cơ chế dựa trên chứng thư số, tính bởi phần tử Π'.
Trong các cơ chế dựa trên chứng thư số, Π' được tính trong E như sau:
Π' = YmGn
Với m = -A-1Bmod q và n = -A-1Cmod q.
Trong các cơ chế dựa trên định danh, nó được mô tả cụ thể trong các cơ chế.
5.3.6 Tính lại bằng chứng
Các tính toán ở bước này như trong 5.2.5. Người kiểm tra thực thi hàm bằng chứng. Các đầu vào Π' từ 5.3.5 và M1 từ 5.3.3. Các đầu ra được tính lại bằng chứng, R'.
Trong cơ chế IBS-2 được đặc tả trong 7.2, quá trình tính toán lại bằng chứng là tính toán hai hàm kiểm tra thay vì tính R'.
5.3.7 Kiểm tra bằng chứng
Chữ ký số được kiểm tra nếu tính lại bằng chứng R' từ 5.3.6 bằng với R từ 5.3.2.
Trong cơ chế IBS-2 được đặc tả trong 7.2, tiến trình kiểm tra bằng chứng liên quan đến việc kiểm tra xem hai giá trị của hàm kiểm tra được tính trong 5.3.6 có giống hệt nhau không thay vì kiểm tra R = R'.

Hình 2 - Tiến trình kiểm tra với bằng chứng ngẫu nhiên
6 Các cơ chế dựa trên chứng thư số
Trong số học đường cong elliptic, một điểm của đường cong được biểu diễn như tọa độ affine. Nghĩa là, một điểm Π của đường cong có hai tọa độ: tọa độ x, Πx, và tọa độ y, Πy. Các đường cong elliptic cho EC-DSA, EC-KCDSA, EC-GDSA, EC-RDSA EC-SDSA và EC-FSDSA bị hạn chế với các đường cong không kì dị và không siêu kì dị.
Các hàm băm định danh có thể được dùng để ràng buộc cơ chế chữ ký và hàm băm.
6.2.1 Tổng quan
DSA (Thuật toán chữ ký số) là cơ chế chữ ký với ![]() , p là một số nguyên tố, và q là một số nguyên tố là ước của p - 1. Tham số D của DSA bằng 1. Thông điệp được chuẩn bị M1 là rỗng và M2 là thông điệp được ký, nghĩa là M2 = M. Hàm bằng chứng được xác định theo công thức:
, p là một số nguyên tố, và q là một số nguyên tố là ước của p - 1. Tham số D của DSA bằng 1. Thông điệp được chuẩn bị M1 là rỗng và M2 là thông điệp được ký, nghĩa là M2 = M. Hàm bằng chứng được xác định theo công thức:
R = Π mod q, với Π = Gkmod p với một vài số nguyên K nào đó.
Và hàm nhiệm vụ theo công thức:
(T1,T2) = (-R, -BS2I(γ, H)),
Với H = h(M) là mã băm cắt ngắn của thông điệp M, được biến đổi thành một số nguyên theo quy luật biến đổi được đưa trong Phụ lục B.
Các hệ số (A, B, C) của chữ ký số DSA được đặt như sau:
(A, B, C) = (S,T1,T2)
Do vậy, công thức ký trở thành:
SK - RX - BS2I(γ, H) ≡ 0(mod q)
CHÚ THÍCH Cơ chế này được lấy từ viện dẫn [17]. Các ký hiệu được thay đổi một chút so với viện dẫn [17] để phù hợp với các ký hiệu được sử dụng trong một vài nơi của tiêu chuẩn này.
6.2.2 Các tham số
p, số nguyên tố, với 2α-1 < p < 2α.
q, ước nguyên tố của p - 1, với 2β-1 < q < 2β.
G, phần tử của nhóm con bậc q, với 1 < G < p.
Với bốn lựa chọn cặp (α, β) được cho phép trong DSA, là (1024,160), (2048, 224), (2048, 256) và (3072, 256). Được khuyến cáo về độ an toàn của cặp (α, β) và γ là như nhau, trừ khi có sự thỏa thuận được thực hiện giữa các bên tham gia để dùng hàm băm mạnh hơn.
Các số nguyên p, q và G có thể được công khai và có thể là chung cho một nhóm người dùng.
Các tham số p, q, G được sinh như đặc tả trong phụ lục D. Nếu phù hợp với tiêu chuẩn của NIST không được yêu cầu thì các tham số p và q có thể được tạo ra nhờ kỹ thuật sinh số nguyên tố trong ISO/IEC 18032.
Một khuyến nghị cho mọi người kiểm tra việc sinh hợp lệ các tham số công khai DSA theo viện dẫn [17].
CHÚ THÍCH Nếu người ký được tự do lựa chọn các tham số miền q để tạo điều kiện cho một va chạm giữa cốc giá trị băm, một tấn công đối với một trường hợp như vậy của DSA có thể được gắn kết trong các yêu cầu va chạm của hàm băm cơ bản có thể được tìm thấy với độ phức tạp là 274, 2101, 2114 (tương ứng với y = 160, 224, 256) được đề xuất như là trường hợp an toàn nhất, trong đó độ phức tạp để tìm va chạm sẽ là 280, 2112, 2128[39]. Tuy nhiên, tấn công va chạm dễ dàng bị phát hiện. Hơn nữa, tấn công không thể gắn kết khi các tham số miền được sinh ra, như đặc tả trong viện dẫn [17], bao gồm phương pháp được đặc tả trong phụ lục D. Nếu không thể xác minh được việc sử dụng một phương pháp thích hợp để tạo ra các tham số miền thì việc tấn công vẫn có thể được ngăn chặn bằng cách sử dụng các cơ chế mẫu được đặc tả trong các Điều 6.3, 6.4 và 6.7.
Chữ ký số dựa trên SHA-1 được khuyến cáo sử được dùng trong các ứng dụng mang tính kế thừa.
6.2.3 Sinh khóa ký và khóa kiểm tra
Khóa ký của một chủ thể ký là một số nguyên bí mật X được sinh giả ngẫu nhiên hoặc ngẫu nhiên sao cho 0 < X < q. Tham số D là 1. Tương ứng với khóa kiểm tra công khai Y là Y = GXmod p.
Một khóa ký bí mật X của người dùng và khóa kiểm tra công khai Y thường được cố định cho một chu kỳ thời gian. Khóa ký X được giữ bí mật.
6.2.4 Tiến trình trình ký
6.2.4.1 Sinh số ngẫu nhiên
Chủ thể ký tính toán số nguyên K ngẫu nhiên hoặc giả ngẫu nhiên sao cho 0 < K < q.
6.2.4.2 Tạo tiền chữ ký
Đầu vào của bước này là số ngẫu nhiên K, và chủ thể ký tính:
Π = GKmod p
6.2.4.3 Chuẩn bị thông điệp để ký
Thông điệp được chuẩn bị sao cho M1 là rỗng và M2 là thông điệp được ký, nghĩa là M2 = M.
6.2.4.4 Tính toán bằng chứng
Chủ thể ký tính R = Πmod q, với bằng chứng chỉ đơn giản là một hàm của tiền chữ ký. Vì vậy
R = (GKmod p)mod q
6.2.4.5 Tính toán nhiệm vụ
Chủ thể ký tính toán mã băm; nếu độ dài đầu ra theo bit của hàm băm lựa chọn lớn hơn [log2 q], H là tập hợp trái nhất (trọng số cao nhất) [log2 q] bit của h(M2). Ngược lại, H là h(M2). Sau đó, H được chuyển đổi thành số nguyên theo quy tắc chuyển đổi, BS2I, trong phụ lục B. Nhiệm vụ (T1,T2) là (-R, -BS2I(γ,H)).
6.2.4.6 Tính toán thành phần thứ hai của chữ ký
Các chữ ký là (R, S) với R được tính trong 6.2.4.4 và
S = (K-1(BS2I(γ, H) + XR))mod q
Với H = vị trí trái nhất (trọng số cao nhất) min(β, γ) bits của h(M2).
Giá trị của h(M2) là một xâu đầu ra γ bit của hàm băm phù hợp trong 6.2.2. Để tính S, chuỗi này sẽ được biến đổi thành số nguyên.
Nó được yêu cầu để kiểm tra R = 0 hoặc S = 0. Nếu một trong hai giá trị R hoặc S = 0, một giá trị mới của K được tạo ra và chữ ký được tính lại (rất hiếm khi xảy ra R = 0 hoặc S = 0 nếu chữ ký số được sinh đúng).
6.2.4.7 Xây dựng phần phụ lục
Phần phụ lục là phép ghép của (R, S) và một trường lựa chọn text, text, ((R,S), text).
6.2.4.8 Xây dựng thông điệp đã ký
Một thông điệp đã ký là phép ghép của thông điệp M và phần phụ lục.
M||((R, S), text)
6.2.5 Tiến trình kiểm tra
6.2.5.1 Tổng quan
Trước khi kiểm tra chữ ký của thông điệp đã ký, người kiểm tra cần phải có các bản sao tin cậy của p, q, G và Y.
6.2.5.2 Truy xuất bằng chứng
Người kiểm tra truy xuất bằng chứng R và thành phần thứ hai của chữ ký S từ phần phụ lục. Và kiểm tra xem 0 < R < q và 0 < S < q. Nếu một trong hai điều kiện bị vi phạm, chữ ký sẽ bị từ chối.
6.2.5.3 Chuẩn bị thông điệp để kiểm tra
Người kiểm tra truy xuất M2 = M từ thông điệp đã ký. M1 là rỗng.
6.2.5.4 Truy xuất nhiệm vụ
Bước này giống với 6.2.4.5. Các đầu vào cho hàm nhiệm vụ bao gồm bằng chứng R từ 6.2.5.2 và M2 từ 6.2.5.3. Nhiệm vụ T = (T1, T2) được tính lại như là đầu ra của hàm nhiệm vụ 6.2.4.5.
6.2.5.5 Tính lại tiền chữ ký
Các đầu vào cho bước này là các tham số miền, khóa kiểm tra Y, nhiệm vụ T = (T1,T2) từ 6.2.5.4 và thành phần thứ 2 của chữ ký số S từ 6.2.5.2. Người kiểm tra có được một giá trị tính lại Π' của tiền chữ ký dùng công thức:
Π' = Y-S-1T1modqG-S-1T2modqmod p
6.2.5.6 Tính lại bằng chứng
Việc tính toán ở bước này giống như 6.2.4.4. Người kiểm tra thực hiện hàm bằng chứng. Đầu vào là Π' từ 6.2.5 5. Lưu ý rằng M1 là rỗng. Đầu ra là bằng chứng được tính lại R' sao cho R' = Π'mod q.
6.2.5.7 Kiểm tra bằng chứng
Người kiểm tra so sánh bằng chứng tính lại, R' từ 6.2.5.6 với giá trị của R từ 6.2.5.2. Nếu R' = R, thì chữ ký là hợp lệ.
6.3.1 Tổng quan
KCDSA (Thuật toán chữ ký số dựa trên chứng thư của Hàn Quốc) là cơ chế chữ ký với ![]() , p là số nguyên tố, và q là ước nguyên tố của p - 1. Khóa kiểm tra Y là GX-1; đó là, tham số D là -1. Thông điệp được chuẩn bị sao cho M1 là rỗng và M2 là thông điệp đã ký, nghĩa là M2 = M. Hàm bằng chứng được xác định theo công thức:
, p là số nguyên tố, và q là ước nguyên tố của p - 1. Khóa kiểm tra Y là GX-1; đó là, tham số D là -1. Thông điệp được chuẩn bị sao cho M1 là rỗng và M2 là thông điệp đã ký, nghĩa là M2 = M. Hàm bằng chứng được xác định theo công thức:
R = h(I2BS(β, Π))
Nếu γ là dài hơn β, thì hàm bằng chứng được thay thế bởi công thức :
R = I2BS(β, BS2I (γ, h(I2BS(β, Π))) mod 2β)
Các tham số miền sẽ chỉ định vào hàm băm được dùng. Hàm nhiệm vụ được xác định theo công thức sau:
(T1,T3) = (V,-1),
Với V = BS2I(β, R ![]() H)mod q. Giá trị H là mã băm từ khóa công khai Y và thông điệp M.
H)mod q. Giá trị H là mã băm từ khóa công khai Y và thông điệp M.
Các hệ số (A, B, C) của công thức chữ ký KCDSA như sau :
(A, B, C) = (T2,S,T1)
Vì vậy, công thức chữ ký số trở thành:
-K + SX-1 + V = 0(mod q)
CHÚ THÍCH Cơ chế này được lấy từ mục [36], Các ký hiệu được thay đổi một chút so với tham chiếu [36] để phù hợp với ký hiệu được dùng trong các phần khác của bộ tiêu chuẩn này.
6.3.2 Các tham số
p một số nguyên tố, với 2α-1 < p < 2α
q một ước nguyên tố của p-1, với 2β-1 < q < 2β
F một số nguyên sao cho 1 < F < p - 1 và F(p-1)/qmod p > 1.
G F(p-1)/qmod p, một phần tử bậc q trong ![]()
l kích thước khối đầu vào (theo bit) của hàm băm được lựa chọn h
Hàm băm của người xác thực hoặc OID với hàm băm được đặc tả.
Ba lựa chọn của bộ ba (α, β, h) được cho phép trong KCDSA, chúng là (2048, 224, SHA-224), (3072, 256, SHA-256) và (2048,224, SHA-256). Giữa chúng, (2048,224,SHA-224) và (3072, 256, SHA-256) được khuyến nghị, còn (2048, 224, SHA-256) có thể được dùng trong trường hợp chỉ có SHA-256 và SHA-224 thì không.
Các số nguyên p, q, G và l có thể được công khai và có thể chung cho một nhóm người dùng.
6.3.3 Sinh khóa ký và khóa kiểm tra
Khóa ký của một chủ thể ký là một số nguyên bí mật X được sinh giả ngẫu nhiên hoặc ngẫu nhiên sao cho 0 < X < q. Tham số D là -1. Tương ứng với khóa kiểm tra công khai Y là Y = GX-1 mod p.
Một khóa ký bí mật X của người dùng và khóa kiểm tra công khai Y thường được cố định cho một chu kỳ thời gian. Khóa ký X được giữ bí mật.
6.3.4 Tiến trình ký
6.3.4.1 Sinh số ngẫu nhiên
Chủ thể ký tính toán số nguyên K ngẫu nhiên hoặc giả ngẫu nhiên sao cho 0 < K < q
6.3.4.2 Tạo tiền chữ ký
Đầu vào của bước này là số ngẫu nhiên K, và chủ thể ký tính
Π = GK mod p
6.3.4.3 Chuẩn bị thông điệp để ký
Thông điệp được chuẩn bị sao cho M1 là rỗng và M2 là thông điệp được ký, nghĩa là M2 = M.
6.3.4.4 Tính toán bằng chứng
Chủ thể ký tính bằng chứng R = h(I2BS(β, Π)), trong đó đầu ra của H là mã băm của xâu bit độ dài α được chuyển đổi từ tiền chữ ký Π. Nếu γ dài hơn β, khi đó việc tính toán bằng chứng được thay thế bởi R = l2BS(β, BS2l (γ, h(I2BS(β, Π))mod 2β).
Quy tắc chuyển đổi, I2BS và BS2I được đưa ra trong phụ lục B.
6.3.4.5 Tính toán nhiệm vụ
Chủ thể ký tính toán nhiệm vụ (T1,T2) = (V, -1) với V = BS2l(β, R ![]() H)mod q, với H = h(Y' ||M2) là mã băm của phép ghép Y' = I2BS(l, Ymod 2l) và thông điệp M2. Giá trị của Y' là một xâu bit có độ dài l. Trong tính toán V, xâu bit R
H)mod q, với H = h(Y' ||M2) là mã băm của phép ghép Y' = I2BS(l, Ymod 2l) và thông điệp M2. Giá trị của Y' là một xâu bit có độ dài l. Trong tính toán V, xâu bit R![]() H sẽ được chuyển đổi thành số nguyên trước khi giảm modulo đối với q.
H sẽ được chuyển đổi thành số nguyên trước khi giảm modulo đối với q.
Nếu γ dài hơn β, thì việc tính toán H được thay thế bởi H = I2BS(β, BS2l(γ, h (Y' || M2))mod 2β).
CHÚ THÍCH Y' là một giá trị cố định cho người dùng, giá trị này có thể được giữ như là tham số của người dùng.
6.3.4.6 Tính toán thành phần thứ hai của chữ ký
Chữ ký là (R, S) với R được tính trong 6.3.4.4 và
S = X(K - V)mod q
6.3.4.7 Xây dựng phần phụ lục
Phần phụ lục là phép ghép của (R, S) và một trường lựa chọn text, text, ((R,S), text).
6.3.4.8 Xây dựng thông điệp đã ký
Một thông điệp đã ký là phép ghép của thông điệp M và phần phụ lục.
M ||((R, S), text)
6.3.5 Tiến trình kiểm tra
6.3.5.1 Tổng quan
Trước khi kiểm tra chữ ký của thông điệp đã ký, người kiểm tra cần phải có các bản sao tin cậy của p, q và G
Người kiểm tra cũng yêu cầu các dữ liệu cần thiết cho tiến trình kiểm tra: ví dụ, khóa kiểm tra Y (xem TCVN 12214-1 (ISO/IEC 14888-1 :2008), Điều 9 cho các yêu cầu bổ sung).
6.3.5.2 Truy xuất bằng chứng
Người kiểm tra truy xuất bằng chứng R và thành phần thứ hai của chữ ký S từ phần phụ lục. Và kiểm tra xem các điều kiện sau có thỏa mãn hay không:
- 0 < S < q ;
- Nếu độ dài của giá trị γ không dài hơn β, độ dài bit của R bằng độ dài bít đầu ra của hàm băm được dùng h ;
- Nếu độ dài của giá trị γ là dài hơn β, độ dài bit của R là bằng β.
Nếu vi phạm bất kỳ điều kiện nào ở trên chữ ký số sẽ bị từ chối.
6.3.5.3 Chuẩn bị thông điệp để kiểm tra
Người kiểm tra truy xuất M2 = M từ thông điệp đã ký. M1 là rỗng.
6.3.5.4 Truy xuất nhiệm vụ
Bước này giống với 6.3.4.5. Các đầu vào cho hàm nhiệm vụ bao gồm bằng chứng R từ 6.3.5.2 và M2 từ 6.3.5.3. Nhiệm vụ T = (T1,T2) được tính lại như là đầu ra của hàm nhiệm vụ 6.3.4.5.
6.3.5.5 Tính lại tiền chữ ký
Đầu vào của bước này là các tham số miền, khóa kiểm tra Y, nhiệm vụ T = (T1,T2) từ 6.3.5.4 và phần thứ hai của chữ ký số S từ 6.3.5.2. Người kiểm tra nhận được giá trị tính toán lại Π' của tiền chữ ký nhờ công thức:
Π' = YS mod q GT1 mod q mod p
6.3.5.6 Tính lại bằng chứng
Việc tính toán ở bước này giống như 6.3.4.4. Người kiểm tra thực hiện hàm bằng chứng. Đầu vào là Π' từ 6.3.5.5. Lưu ý rằng M1 là rỗng. Đầu ra là bằng chứng được tính lại R'
6.3.5.7 Kiểm tra bằng chứng
Người kiểm tra so sánh bằng chứng tính lại, R' từ 6.3.5.6 với giá trị của R từ 6.3.5.2. Nếu R' = R, thì chữ ký là hợp lệ.
6.4 Thuật toán Pointcheval/Vaudenay
6.4.1 Tổng quan
Phương pháp của Pointcheval/Vaudenay là một biến thể của thuật toán DSA, với ![]() , p là một số nguyên tố, và q là một ước nguyên tố của p - 1. Tham số D bằng 1. Thông điệp được chuẩn bị sao cho M1 là rỗng và M2 là thông điệp được ký, nghĩa là M2 = M. Bằng chứng được xác định bởi công thức :
, p là một số nguyên tố, và q là một ước nguyên tố của p - 1. Tham số D bằng 1. Thông điệp được chuẩn bị sao cho M1 là rỗng và M2 là thông điệp được ký, nghĩa là M2 = M. Bằng chứng được xác định bởi công thức :
R = Π mod q
Và hàm nhiệm vụ được xác định bởi công thức
(T1,T2) = (-R, -H)
Với H = h(I2BS(β, R)||M) là mã băm của phép ghép của bằng chứng R và thông điệp M. Lưu ý rằng việc tính T2 trên yêu cầu việc biến đổi mã băm thành một số nguyên. Hàm biến đổi được đưa ra trong phụ lục B.
Các hệ số (A, B, C) của công thức chữ ký Pointcheval/Vaudenay như sau:
(A, B, C) = (S,T1,T2)
Vì vậy công thức ký là:
SK - RX - H ≡ 0(mod q)
CHÚ THÍCH Cơ chế này dựa trên thuật toán được thiết kế bởi D. Pointcheval và S. Vaudenay trong viện chiếu [31].
6.4.2 Các tham số
p một số nguyên tố
q một ước nguyên tố của p - 1
F một số nguyên sao cho 1 < F < p - 1 và F(p-1)/q mod p > 1
G F(p-1)/qmod p
Hàm băm định danh hoặc OID với hàm băm được đặc tả
Một khuyến nghị cho mọi người kiểm tra việc sinh các tham số công khai hợp lệ.
6.4.3 Sinh khóa ký và khóa kiểm tra
Khóa ký của một chủ thể ký là một số nguyên bí mật X được sinh giả ngẫu nhiên hoặc ngẫu nhiên sao cho 0 < X < q. Tham số D là 1. Khóa kiểm tra công khai tương ứng Y là:
Y = GX mod p
Một khóa ký bí mật X của người dùng và khóa kiểm tra công khai Y thường được cố định cho một chu kỳ thời gian. Khóa ký X được giữ bí mật.
6.4.4 Tiến trình ký
6.4.4.1 Sinh số ngẫu nhiên
Chủ thể ký tính toán số nguyên K ngẫu nhiên hoặc giả ngẫu nhiên sao cho 0 < K < q
6.4.4.2 Tạo tiền chữ ký
Đầu vào của bước này là số ngẫu nhiên K và chủ thể ký tính:
Π = GK mod p
6.4.4.3 Chuẩn bị thông điệp để ký
Thông điệp được chuẩn bị sao cho M1 là rỗng và M2 là thông điệp được ký, nghĩa là M2 = M.
6.4.4.4 Tính toán bằng chứng
Chủ thể ký tính toán R = Πmod q, với bằng chứng đơn giản là một hàm của tiền chữ ký. Vì vậy, R = (GK mod p)mod q.
6.4.4.5 Tính toán nhiệm vụ
Chủ thể ký tính nhiệm vụ (T1,T2) = (-R, -BS2I(γ, H)), với H = h(I2BS(β, R)||M2) là mã băm của việc ghép bằng chứng và thông điệp M2. Trước khi ghép, bằng chứng sẽ được biến đổi thành xâu bit độ dài |p|.
6.4.4.6 Tính chữ ký
Chữ ký là (R, S) với R được tính ở 6.4.4.4 và
S = K-1(BS2I(γ, H) + XR)mod q.
6.4.4.7 Xây dựng phần phụ lục
Phần phụ lục là phép ghép của (R, S) và một trường lựa chọn text, text, ((R, S), text).
6.4.4.8 Xây dựng thông điệp đã ký
Một thông điệp đã ký là phép ghép của thông điệp M và phần phụ lục.
M||((R, S), text)
6.4.5 Tiến trình kiểm tra
6.4.5.1 Tổng quan
Trước khi kiểm tra chữ ký của thông điệp đã ký, người kiểm tra cần phải có các bản sao tin cậy của p, q, G.
Người kiểm tra cũng yêu cầu các dữ liệu cần thiết cho tiến trình kiểm tra: ví dụ, khóa kiểm tra Y (xem TCVN 12214-1 (ISO/IEC 14888-1:2008), Điều 9 cho các yêu cầu bổ sung).
6.4.5.2 Truy xuất bằng chứng
Người kiểm tra truy xuất bằng chứng R và thành phần thứ hai của chữ ký S từ phần phụ lục. Và kiểm tra xem 0 < R < q va 0 < S < q. Nếu một trong các điều kiện bị vi phạm, chữ ký số sẽ bị từ chối.
6.4.5.3 Chuẩn bị thông điệp để kiểm tra
Người kiểm tra truy xuất M2 = M từ thông điệp đã ký. M1 là rỗng.
6.4.5.4 Truy xuất nhiệm vụ
Bước này giống với 6.4.4.5. Các đầu vào cho hàm nhiệm vụ bao gồm bằng chứng R từ 6.4.5.2 và M2 từ 6.4.5.3. Nhiệm vụ T = (T1,T2) được tính lại như là đầu ra của hàm nhiệm vụ 6.4.4.5.
6.4.5.5 Tính lại tiền chữ ký
Các đầu vào cho bước này là các tham số miền, khóa kiểm tra Y, nhiệm vụ T = (T1,T2) từ 6.4.5.4 và thành phần thứ 2 của chữ ký số S từ 6.4.5.2. Người kiểm tra có được một giá trị tính lại Π' của tiền chữ ký dùng công thức:
Π' = Y-S-1T1mod q G-S-1T2 mod q mod p
6.4.5.6 Tính lại bằng chứng
Việc tính toán ở bước này giống như 6.4.4.4. Người kiểm tra thực hiện hàm bằng chứng. Đầu vào là Π' từ 6.4.5.5. Lưu ý rằng M1 là rỗng. Đầu ra là bằng chứng được tính lại R'
6.4.5.7 Kiểm tra bằng chứng
Người kiểm tra so sánh bằng chứng tính lại, R' từ 6.4.5.6 với giá trị của R từ 6.4 5.2. Nếu R' = R, thì chữ ký là hợp lệ
6.5.1 Tổng quan
SDSA (Thuật toán chữ ký số Schnorr) là một cơ chế chữ ký với ![]() p là một số nguyên tố, và q là một ước nguyên tố của p - 1. Tham số D = 1. Thông điệp chuẩn bị sao cho M1 là thông điệp được ký, nghĩa là M1 = M, và M2 là rỗng. Hàm bằng chứng được xác định bằng cách đặt R bằng một mã băm. Hàm nhiệm vụ được xác định bằng cách đặt T1 = -1 và T2 là số nguyên âm nhận được bằng cách chuyển đổi R thành một số nguyên theo quy tắc BS2I, được đưa ra trong Phụ lục B và sau đó rút gọn modulo q.
p là một số nguyên tố, và q là một ước nguyên tố của p - 1. Tham số D = 1. Thông điệp chuẩn bị sao cho M1 là thông điệp được ký, nghĩa là M1 = M, và M2 là rỗng. Hàm bằng chứng được xác định bằng cách đặt R bằng một mã băm. Hàm nhiệm vụ được xác định bằng cách đặt T1 = -1 và T2 là số nguyên âm nhận được bằng cách chuyển đổi R thành một số nguyên theo quy tắc BS2I, được đưa ra trong Phụ lục B và sau đó rút gọn modulo q.
Các hệ số (A, B, C) của công thức ký SDSA được tính như sau:
(A, B, C) = (T1,T2,S).
Vì vậy, công thức ký trở thành:
-K + T2X + S ≡ 0 (mod q).
CHÚ THÍCH SDSA là viết tắt của Thuật toán chữ ký số Schnorr. Cơ chế được lấy từ viện dẫn [32] và [33], Các ký hiệu được thay đổi so với viện dẫn [32] và [33] để phù hợp với ký hiệu được dùng trong tiêu chuẩn này.
6.5.2 Các tham số
p số nguyên tố, với 2α-1 < p < 2α.
q một ước số nguyên tố của p - 1, với 2β-1 < q < 2β.
G một phần tử sinh của nhóm con bậc q, sao cho 1 < G < q.
Bốn sự lựa chọn cho cặp (α, h) được cho phép trong SDSA, được gọi là (1024, SHA-1), (2048, SHA-224) và (3072, SHA-256). β tương ứng được lựa chọn là α trong Bảng 1.
Các số nguyên p, q, G có thể được công khai và có thể chung cho một nhóm người dùng.
Các tham số p, q, G được sinh như trong đặc tả ở phụ lục D. Các tham số p và q có thể được sinh ra bằng cách sử dụng kỹ thuật sinh số nguyên tố trong ISO/IEC 18032.
Một khuyến nghị đối với toàn bộ người dùng kiểm tra việc sinh hợp lệ của các tham số công khai SDSA theo viện dẫn [17].
Một khuyến nghị đối với chữ ký số dựa trên SHA-1 chỉ nên sử dụng cho các ứng dụng mang tính kế thừa.
6.5.3 Sinh khóa ký và khóa kiểm tra
Khóa ký của một chủ thể ký là một số nguyên bí mật X được sinh giả ngẫu nhiên hoặc ngẫu nhiên sao cho 0 < X < q. Tham số D là 1. Tương ứng với khóa kiểm tra công khai Y là Y = GX mod p.
Một khóa ký bí mật X của người dùng và khóa kiểm tra công khai Y thường được cố định cho một chu kỳ thời gian. Khóa ký X được giữ bí mật
6.5.4 Tiến trình ký
6.5.4.1 Tạo số ngẫu nhiên
Chủ thể ký tính toán số nguyên K ngẫu nhiên hoặc giả ngẫu nhiên sao cho 0 < K < q
6.5.4.2 Tạo tiền chữ ký
Đầu vào của bước này là số ngẫu nhiên K, và chủ thể ký tính
Π = GK mod p.
6.5.4.3 Chuẩn bị thông điệp để ký
Thông điệp được chuẩn bị sao cho M1 là thông điệp được ký, nghĩa là M1 = M, và M2 là rỗng.
6.5.4.4 Tính bằng chứng
Chủ thể ký tính bằng chứng R là mã băm của tiền chữ ký Π và phần đầu tiên của thông điệp M1
R = h(I2BS(β, Π)||M).
6.5.4.5 Tính nhiệm vụ
Giá trị của bằng chứng R được biến đổi thành một số nguyên theo quy tắc biến đổi, BS2I, trong phụ lục B và sau đó rút gọn theo modulo q. Nhiệm vụ (T1,T2) là (-1,-BS2I(γ, R)mod q).
6.5.4.6 Tính toán thành phần thứ hai của chữ ký
Chữ ký số (R, S) với S = (K + BS2I(γ, R)X)mod q.
Như một sự lựa chọn, một mong muốn để kiểm tra nếu R = 0 hoặc S = 0. Nếu một trong hai giá trị R = 0 hoặc S = 0, một giá trị mới của K được sinh ra và chữ ký được tính toán lại (rất hiếm khi xảy ra R = 0 hoặc S = 0 nếu chữ ký số được sinh đúng).
6.5.4.7 Xây dựng phần phụ lục
Phần phụ lục là phép ghép của (R, S) và một trường lựa chọn text, text.
6.5.4.8 Xây dựng thông điệp đã ký
Một thông điệp đã ký là phép ghép của thông điệp M và phần phụ lục.
M||((R,S), text)
6.5.5 Tiến trình kiểm tra
6.5.5.1 Tổng quan
Chủ thể kiểm tra yêu cầu dữ liệu cần thiết được yêu cầu cho tiến trình kiểm tra.
6.5.5.2 Truy xuất bằng chứng
Người kiểm tra truy xuất bằng chứng R và thành phần thứ hai của chữ ký S từ phần phụ lục. Người kiểm tra kiểm tra xem R là một xâu khác 0 trong dải của hàm băm hay không và sao cho 0 < S < q.
6.5.5.3 Chuẩn bị thông điệp để kiểm tra
Người kiểm tra truy xuất M từ thông điệp đã ký và chia thông điệp thành hai phần M1 và M2, sao cho M1 = M và M2 là rỗng.
6.5.5.4 Truy xuất nhiệm vụ
Đầu vào của hàm nhiệm vụ bao gồm bằng chứng R từ 6.5.5.2. Nhiệm vụ
T = (T1,T2) = (-1, -BS2l(γ, R)mod q).
6.5.5.5 Tính lại tiền chữ ký
Các đầu vào cho bước này là các tham số miền, khóa kiểm tra Y, nhiệm vụ T = (T1,T2) từ 6.5.5.4 và thành phần thứ 2 của chữ ký số S từ 6 5.5.2. Người kiểm tra có được một giá trị tính lại Π' của tiền chữ ký dùng công thức
Π'=Y(T2 mod q) G(-ST1 mod q) mod p = Y(T2 mod q) G(S mod q) mod p
6.5.5.6 Tính lại bằng chứng
Việc tính ở bước này là giống như trong 6.5.4.4 và 6.5.4.5. Người kiểm tra thực hiện hàm bằng chứng. Đầu vào Π' từ 6.5.5.5 và M1 từ 6.5.5.3. Đầu ra là bằng chứng được tính lại R', là mã băm của việc tính lại tiền chữ ký Π' và thông điệp M.
6.5.5.7 Kiểm tra bằng chứng
Người kiểm tra so sánh với bằng chứng được tính lại R’ từ 6.5.5.6 với phiên bản R truy xuất từ 6.5.5.2. Nếu R’ = R thì chữ ký được kiểm tra.
6.6.1 Tổng quan
EC-DSA (Thuật toán chữ ký số dựa trên đường cong elliptic) là một thuật toán đường cong elliptic liên tục DSA. Các hệ số (A, B, C) của EC-DSA được thiết lập như sau:
(A, B, C) = (S, T1,T2)
Với (T1,T2) = (-R,-BS2l(γ, H)) và H = h(M) là mã băm được cắt ngắn của thông điệp M, được biến đổi thành số nguyên theo quy tắc biến đổi được đưa trong phụ lục B. Hàm băm h là một trong các hàm băm SHA-1, SHA-224, SHA-256, SHA-384 và SHA-512 được mô tả trong TCVN 11816-3:2017 (ISO/IEC 10118-3).
Khóa kiểm tra Y là [X]G; nghĩa là tham số D bằng 1. Thông điệp được chuẩn bị sao cho M1 là rỗng và M2 là thông điệp được ký, nghĩa là M2 = M. Hàm bằng chứng được xác định theo công thức
R = FE2l(r, ΠX)mod q
Quy tắc biến đổi, FE2I, được đưa ra trong Phụ lục B.
Vì vậy, công thức chữ ký trở thành
SK - RX - BS2l (γ, H) ≡ 0(mod q)
CHÚ THÍCH Cơ Chế này dựa trên thuật toán được mô tả tại viện dẫn [7].
6.6.2 Các tham số
F Một trường hữu hạn
E một nhóm đường cong elliptic trên trường F.
#E lực lượng của E
q một ước nguyên tố của #E
G một điểm của đường cong elliptic bậc q
Mọi tham số có thể được công khai và có thể dùng chung cho một nhóm người dùng. Độ dài an toàn của hàm băm được lựa chọn nên trùng hoặc vượt quá độ dài an toàn liên quan đến độ dài bit q.
Một khuyến nghị đối với toàn bộ người dùng kiểm tra việc sinh hợp lệ của các tham số công khai EC-DSA theo viện dẫn [7] hoặc [17],
Một khuyến nghị đối với chữ ký số dựa trên SHA-1 chỉ nên sử dụng cho các ứng dụng mang tính kế thừa.
6.6.3 Sinh khóa ký và khóa kiểm tra
Khóa ký của một chủ thể ký là một số nguyên bí mật X được sinh giả ngẫu nhiên hoặc ngẫu nhiên sao cho 0 < X < q. Tham số D là 1. Tương ứng với khóa kiểm tra công khai Y là
Y = [X] G.
Một khóa ký bí mật X của người dùng và khóa kiểm tra công khai Y thường được cố định cho một chu kỳ thời gian. Khóa ký X được giữ bí mật
6.6.4 Tiến trình ký
6.6.4.1 Tạo số ngẫu nhiên
Chủ thể ký tính toán một số nguyên K ngẫu nhiên hoặc giả ngẫu nhiên sao cho 0 < K < q.
6.6.4.2 Tạo tiền chữ ký
Đầu vào của bước này là số ngẫu nhiên K và chủ thể ký tính
Π = [K]G.
6.6.4.3 Chuẩn bị thông điệp để ký
Thông điệp được chuẩn bị sao cho M1 là rỗng và M2 là thông điệp được ký, nghĩa là M2 = M.
6.6.4.4 Tính bằng chứng
Chủ thể ký tính R = FE2I(r, ΠX)mod q.
6.6.4.5 Tính nhiệm vụ
Chủ thể ký tạo ra mã băm; nếu độ dài theo bit đầu ra của hàm băm lớn hơn [log2q], H được thiết lập phía trái nhất (trọng số cao nhất) [log2q] của h(M2). Ngược lại, H là h(M2). Sau đó, H được biến đổi thành số nguyên theo quy tắc biến đổi BS2I, trong phụ lục B. Nhiệm vụ (T1,T2) là (-R, -BS2I(γ, H)).
6.6.4.6 Tính thành phần thứ hai của chữ ký
Chữ ký là (R, S) với R được tính trong 6.6.4.4 và
S = (K-1 (XR + BS2I(γ, H))) mod q.
Nó được yêu cầu để kiểm tra R = 0 hoặc S = 0. Nếu một trong hai giá trị R hoặc S = 0, một giá trị mới của K được tạo ra và chữ ký được tính lại (rất hiếm khi xảy ra R = 0 hoặc S = 0 nếu chữ ký số được sinh đúng).
6.6.4.7 Xây dựng phần phụ lục
Phần phụ lục là phép ghép của (R, S) và một trường lựa chọn text, text, ((R, S), text)
6.6.4.8. Xây dựng thông điệp đã ký
Một thông điệp đã ký là việc ghép của M và phần phụ lục.
M||((R, S), text)
6.6.5 Tiến trình kiểm tra
6.6.5.1 Tổng quan
Chủ thể kiểm tra yêu cầu dữ liệu cần thiết được yêu cầu cho tiến trình kiểm tra.
6.6.5.2 Truy xuất bằng chứng
Người kiểm tra truy xuất bằng chứng R và thành phần thứ hai của chữ ký S từ phần phụ lục. Để kiểm tra xem 0 < R < q và 0 < S < q; nếu một trong các điều kiện đó bị vi phạm, chữ ký số sẽ bị từ chối.
6.6.5.3 Chuẩn bị thông điệp để kiểm tra
Người kiểm tra truy xuất M từ thông điệp đã ký và chia thông điệp thành hai phần M1 và M2. M1 là rỗng và M2 = M.
6.6.5.4 Truy xuất nhiệm vụ
Bước này giống với 6.6.4.5. Các đầu của hàm nhiệm vụ bao gồm bằng chứng R từ 6.6.5.2 và M2 từ 6.6.5.3. Nhiệm vụ T = (T1,T2) được tính lại như đầu ra từ hàm nhiệm vụ 6.6.4.5.
6.6.5.5 Tính lại tiền chữ ký
Đầu vào của bước này là hệ thống các tham số, khóa kiểm tra Y, nhiệm vụ (T = T1,T2) từ 6.6.5.4 và phần thứ hai của chữ ký S từ 6.6.5.2. Người kiểm tra có được giá trị tính lại của tiền chữ ký Π' bởi công thức sau
Π'=[-S-1T1mod q]Y + [-S-1T2mod q]G
6.6.5.6 Tính lại bằng chứng
Việc tính toán ở bước này giống với 6.6.4.4. Người kiểm tra thực hiện hàm bằng chứng, Đầu vào Π' từ 6.6.5.5. Đầu ra là bằng chứng được tính lại R'.
6.6.5.7 Kiểm tra bằng chứng
Người kiểm tra so sánh giá trị bằng chứng được tính lại R’ từ 6.6.5.6 với phiên bản R được truy xuất từ 6.6.5.2. Nếu R’ = R thì chữ ký số được kiểm tra.
6.7.1 Tổng quan
EC-KCDSA (Thuật toán chữ ký số dựa trên chứng thư số đường cong elliptic Hàn Quốc) là cơ chế ký với khóa kiểm tra Y = [X-1]G; đó là, tham số D bằng -1. Thông điệp được chuẩn bị sao cho M1 là rỗng và M2 là thông điệp đã được ký, nghĩa là M2 = M. Hàm bằng chứng được xác định theo công thức sau:
R = h(FE2BS(r, ΠX)).
Nếu γ dài hơn β, thì hàm bằng chứng được thay thế bởi công thức
R = I2BS(β, BS2I (γ, h(FE2BS(r, ΠX))) mod 2β)
Các tham số miền sẽ được chỉ thị trong hàm băm được dùng. Các hàm nhiệm vụ được xác định theo công thức:
(T1,T2) = (V, -1)
Với V = BS2I(β, (R ![]() H))mod q. Giá trị H là mã băm từ khóa công khai Y và thông điệp M.
H))mod q. Giá trị H là mã băm từ khóa công khai Y và thông điệp M.
Các hệ số (A, B, C) của EC-KCDSA được thiết lập như sau :
(A, B, C) = (T2,S,T1)
Vì vậy công thức ký trở thành
-K + SX-1 + V ≡ 0(mod q).
CHÚ THÍCH Cơ chế này được lấy từ viện dẫn [37], Các ký hiệu được thay đổi một chút so với viện dẫn [37] để phù hợp với ký hiệu được dùng trong một số nơi khác của tiêu chuẩn này.
6.7.2 Các tham số
l kích thước khối đầu vào (theo bit) của hàm băm đã được lựa chọn h.
F một trường hữu hạn
E một nhóm đường cong elliptic trên trường F
#E lực lượng của E
q ước nguyên tố của #E
G một điểm trên đường cong elliptic bậc q
Định danh hàm băm hoặc OID với hàm băm được đặc tả.
Tất cả các tham số có thể được công khai và có thể dùng chung cho một nhóm người dùng.
Một khuyến nghị đối với toàn bộ người dùng kiểm tra việc sinh hợp lệ của các tham số công khai EC-KCDSA theo viện dẫn [37].
6.7.3 Sinh khóa ký và khóa kiểm tra
Khóa ký của một chủ thể ký là một số nguyên bí mật X được sinh giả ngẫu nhiên hoặc ngẫu nhiên sao cho 0 < X < q. Tham số D là -1. Tương ứng với khóa kiểm tra công khai Y là
Y = [X-1]G
Một khóa ký bí mật X của người dùng và khóa kiểm tra công khai Y thường được cố định cho một chu kỳ thời gian. Khóa ký X được giữ bí mật.
6.7.4 Tiến trình ký
6.7.4.1 Tạo số ngẫu nhiên
Chủ thể ký tính toán một số nguyên K ngẫu nhiên hoặc giả ngẫu nhiên sao cho 0 < K < q.
6.7.4.2 Tạo tiền chữ ký
Đầu vào cho bước này là số ngẫu nhiên K và chủ thể ký tính
Π = [K]G
6.7.4.3 Chuẩn bị thông điệp để ký
Thông điệp được chuẩn bị sao cho M1 là rỗng và M2 là thông điệp được ký, nghĩa là M2 = M.
6.7.4.4 Tính bằng chứng
Chủ thể ký tính R = h(FE2BS(r, ΠX)), với đầu ra của h là mã băm của ΠX. Nếu γ dài hơn β, thì việc tính toán bằng chứng được thay bằng R = I2BS(β, BS2l(8 [log256(r)], FE2BS (r, ΠX)) mod 2β).
Quy tắc biến đổi FE2BS, I2BS và BS2I được đưa ra trong phụ lục B.
6.7.4.5 Tính nhiệm vụ
Chủ thể ký tính nhiệm vụ (T1,T2) = (V, -1) với V = BS2I(β, R ![]() H)mod q, với H = h(Y'||M2) là mã băm của phép ghép Y' và thông điệp M2. Giá trị của Y' là l bit trái nhất của một chuỗi bit FE2BS(r, YX)||FE2BS(r,YY). Nếu l dài hơn độ dài của chuỗi, số 0 được đệm thêm vừa đủ vào cuối chuỗi. Trong việc tính V, xâu bit R
H)mod q, với H = h(Y'||M2) là mã băm của phép ghép Y' và thông điệp M2. Giá trị của Y' là l bit trái nhất của một chuỗi bit FE2BS(r, YX)||FE2BS(r,YY). Nếu l dài hơn độ dài của chuỗi, số 0 được đệm thêm vừa đủ vào cuối chuỗi. Trong việc tính V, xâu bit R ![]() H sẽ được biến đổi thành một số nguyên trước khi rút gọn modulo đối với q.
H sẽ được biến đổi thành một số nguyên trước khi rút gọn modulo đối với q.
Nếu γ dài hơn β, thì việc tính H sẽ được thay thế bằng H = I2BS(β, BS2I(γ, h(Y' ||M2)) mod 2β).
CHÚ THÍCH Y' là một giá trị cố định cho một người dùng, giá trị này có thể được giữ như là một tham số người dùng.
6.7.4.6 Tính toán thành phần thứ hai của chữ ký
Chữ ký (R, S) với R được tính trong 6.7.4.4 và
S = X(K - V)mod q
6.7.4.7 Xây dựng phần phụ lục
Phần phụ lục là phép ghép của (R, S) và một trường lựa chọn text, text, ((R, S), text).
6.7.4.8 Xây dựng thông điệp đã ký
Một thông điệp đã ký là phép ghép thông điệp M và phần phụ lục.
M||((R,S), text)
6.7.5 Tiến trình kiểm tra
6.7.5.1 Tổng quan
Trước khi kiểm tra chữ ký của thông điệp đã ký, người kiểm tra cần phải có các bản sao tin cậy của E, q và G
Người kiểm tra cũng yêu cầu các dữ liệu cần thiết cho tiến trình kiểm tra: ví dụ, khóa kiểm tra Y (xem TCVN 12214-1 (ISO/IEC 14888-1), Điều 9 cho các yêu cầu bổ sung).
6.7.5.2 Truy xuất bằng chứng
Người kiểm tra truy xuất bằng chứng R và thành phần thứ hai của chữ ký S từ phần phụ lục. Người kiểm tra kiểm tra xem các điều sau có thỏa mãn hay không:
- 0 < S < q;
- Nếu độ dài của giá trị γ không dài hơn β, độ dài theo bit của R = h (độ dài đầu ra theo bít của hàm băm được sử dụng);
- Nếu độ dài của giá trị γ dài hơn β, độ dài theo bit của R = β.
Nếu bất kỳ điều nào trong các điều trên không thỏa mãn, chữ ký số sẽ bị từ chối.
6.7.5.3 Chuẩn bị thông điệp để kiểm tra
Người kiểm tra truy xuất M2 = M từ thông điệp đã ký. M1 là rỗng.
6.7.5.4 Truy xuất nhiệm vụ
Bước này giống với 6.7.4.5. Các đầu vào cho hàm nhiệm vụ bao gồm bằng chứng R từ 6.7.5.2 và M2 từ 6.7.5.3. Nhiệm vụ T = (T1,T2) được tính lại như là đầu ra của hàm nhiệm vụ 6.7.4.5
6.7.5.5 Tính lại tiền chữ ký
Các đầu vào cho bước này là các tham số miền, khóa kiểm tra Y, nhiệm vụ T = (T1,T2) từ 6.7.5.4 và thành phần thứ 2 của chữ ký số S từ 6.7.5.2. Người kiểm tra có được một giá trị tính lại Π' của tiền chữ ký dùng công thức:
Π' = [S mod q]Y+ [T1 mod q]G.
6.7.5.6 Tính lại bằng chứng
Việc tính toán ở bước này giống như 6.7.4.4. Người kiểm tra thực hiện hàm bằng chứng. Đầu vào là Π' từ 6.7.5.5. Lưu ý rằng M1 là rỗng. Đầu ra là bằng chứng được tính lại R'
6.7.5.7 Kiểm tra bằng chứng
Người kiểm tra so sánh bằng chứng tính lại, R' từ 6.7.5.6 với giá trị của R từ 6.7.5.2. Nếu R' = R, thì chữ ký là hợp lệ
6.8.1 Tổng quan
EC-GDSA (Thuật toán chữ ký số đường cong elliptic Đức) là cơ chế ký với khóa kiểm tra Y = [X-1]G; đó là tham số D bằng -1. Thông điệp được chuẩn bị sao cho M1 là rỗng và M2 là thông điệp đã được ký, nghĩa là M2 = M. Hàm bằng chứng được xác định theo công thức sau
R = FE2I(r, ΠX)mod q.
Các hệ số (A, B, C) của công thức chữ ký số EC-GDSA được thiết lập như sau:
(A, B, C) = (T1,S,T2)
Với (T1,T2) = (-R, H) và H là mã băm của thông điệp M.
Công thức chữ ký trở thành:
-RK + SX-1 + H ≡ 0 (mod q).
CHÚ THÍCH EC-GDSA là viết tắt của thuật toán chữ ký số của đường cong elliptic Đức.[16]
6.8.2 Các tham số
F một trường hữu hạn
E một nhóm đường cong elliptic trên trường F
#E lực lượng của E
q ước nguyên tố của #E
G một điểm trên đường cong elliptic bậc q
Định danh hàm băm hoặc OID với hàm băm được đặc tả.
Tất cả các tham số có thể được công khai và có thể dùng chung cho một nhóm người dùng.
Một khuyến nghị đối với toàn bộ người dùng kiểm tra việc sinh hợp lệ các tham số công khai.
6.8.3. Sinh khóa ký và khóa kiểm tra
Khóa ký của một chủ thể ký là một số nguyên bí mật X được sinh giả ngẫu nhiên hoặc ngẫu nhiên sao cho 0 < X < q. Tham số D là -1. Tương ứng với khóa kiểm tra công khai Y là
Y = [X-1]G
Một khóa ký bí mật X của người dùng và khóa kiểm tra công khai Y thường được cố định cho một chu kỳ thời gian. Khóa ký X được giữ bí mật
6.8.4 Tiến trình ký
6.8.4.1 Tạo số ngẫu nhiên
Chủ thể ký tính một số nguyên ngẫu nhiên hoặc giả ngẫu nhiên K sao cho 0 < K < q.
6.8.4.2 Tạo tiền chữ ký
Đầu vào của bước này là số ngẫu nhiên K và chủ thể ký tính
Π = [K]G.
6.8.4.3 Chuẩn bị thông điệp để ký
Thông điệp được chuẩn bị sao cho M1 là rỗng và M2 là thông điệp được ký, nghĩa là M2 = M.
6.8.4.4 Tính bằng chứng
Chủ thể ký tính R = FE2I(r, ΠX)mod q với bằng chứng đơn giản chỉ là một hàm của tiền chữ ký.
6.8.4.5 Tính nhiệm vụ
Chủ thể ký tính nhiệm vụ (T1, T2) = (-R, BS2I(γ, H)) với H là mã băm của thông điệp M2.
6.8.4.6 Tính toán thành phần thứ hai của chữ ký
Chữ ký (R, S) với R được tính trong 6.8.4.4 và
S = X(KR - BS2l(γ, H))mod q.
6.8.4.7 Xây dựng phần phụ lục
Phần phụ lục là phép ghép của (R, S) và một trường lựa chọn text, text, ((R,S), text).
6.8.4.8 Xây dựng thông điệp đã ký
Một thông điệp đã ký là phép ghép, M, và phần phụ lục
M||((R,S),text).
6.8.5 Tiến trình kiểm tra
6.8.5.1 Tổng quan
Chủ thể kiểm tra yêu cầu các dữ liệu cần thiết cho tiến trình kiểm tra.
6.8.5.2 Truy xuất bằng chứng
Người kiểm tra truy xuất bằng chứng R và thành phần thứ hai của chữ ký S từ phần phụ lục. Để kiểm tra xem 0 < R < q và 0 < S < q; nếu một trong các điều kiện đó bị vi phạm, chữ ký số sẽ bị từ chối.
6.8.5.3 Chuẩn bị thông điệp để kiểm tra
Người kiểm tra truy xuất M từ thông điệp đã ký và chia thông điệp thành hai phần M1 và M2. M1 là rỗng và M2 = M.
6.8.5.4 Truy xuất nhiệm vụ
Bước này giống với 6.8.4.5. Các đầu vào cho hàm nhiệm vụ bao gồm bằng chứng R từ 6.8.5.2 và M2 từ 6.8.5.3. Nhiệm vụ T = (T1,T2) được tính lại như là đầu ra của hàm nhiệm vụ 6.8.4.5
6.8.5.5 Tính lại tiền chữ ký
Các đầu vào cho bước này là hệ thống các tham số, khóa kiểm tra Y, nhiệm vụ T = (T1,T2) từ 6.8.5.4 và thành phần thứ 2 của chữ ký số S từ 6.8.5.2. Người kiểm tra có được một giá trị tính lại Π' của tiền chữ ký dùng công thức:
Π' = [(-T1))-1S mod q]Y + [(-T1)-1T2 mod q]G.
6.8.5.6 Tính lại bằng chứng
Việc tính toán ở bước này giống như 6.8.4.4. Người kiểm tra thực hiện hàm bằng chứng. Đầu vào là Π' từ 6.8.5.5. Đầu ra là bằng chứng được tính lại R’
6.8.5.7 Kiểm tra bằng chứng
Người kiểm tra so sánh bằng chứng tính lại, R’ từ 6.8.5.6 với giá trị của R từ 6.8.5.2. Nếu R' = R, thì chữ ký là hợp lệ
6.9.1 Tổng quan
EC-RDSA (Thuật toán chữ ký số đường cong elliptic Nga) là cơ chế ký với khóa kiểm tra Y = [X]G; đó là, tham số D bằng 1. Thông điệp được chuẩn bị sao cho M1 là rỗng và M2 là thông điệp đã được ký, nghĩa là M2 = M. Các hệ số (A, B, C) của chữ ký EC-RDSA được thiết lập như sau:
(A, B, C) = (T1,T2, -S)
Với (T1,T2) = (H, R) và H = h(M) là mã băm của thông điệp M, được biến đổi thành một số nguyên như mô tả trong 6.9.4.5.
Hàm bằng chứng được xác định theo công thức sau:
R = FE2I(r, ΠX)mod q.
Vì vậy công thức ký trở thành
HK + RX - S ≡ 0(mod q).
CHÚ THÍCH EC-RDSA là viết tắt của thuật toán đường cong elliptic Nga. Cơ chế này được lấy từ viện dẫn [21]. Các ký hiệu được thay đổi so với viễn dẫn [22] để phù hợp với ký hiệu được dùng trong tiêu chuẩn này.
6.9.2 Các tham số
p một số nguyên tố
E một nhóm đường cong elliptic trên trường GE(p)
#E lực lượng của E
q ước nguyên tố của #E
G một điểm trên đường cong elliptic bậc q
Định danh hàm băm hoặc OID với hàm băm được đặc tả.
Tất cả các tham số có thể được công khai và có thể dùng chung cho một nhóm người dùng.
6.9.3 Sinh khóa ký và khóa kiểm tra
Khóa kỳ của một chủ thể ký là một số nguyên bí mật X được sinh giả ngẫu nhiên hoặc ngẫu nhiên sao cho 0 < X < q. Tham số D là 1. Tương ứng với khóa kiểm tra công khai Y là
Y = [X]G.
Một khóa ký bí mật X của người dùng và khóa kiểm tra công khai Y thường được cố định cho một chu kỳ thời gian. Khóa ký X được giữ bí mật.
CHÚ THÍCH Viện dẫn [21] không hoàn toàn đặc tả tiến trình sinh khóa ký bí mật X của một người dùng.
6.9.4 Tiến trình ký
6.9.4.1 Tạo số ngẫu nhiên
Chủ thể ký tính toán một số nguyên K ngẫu nhiên hoặc giả ngẫu nhiên sao cho 0 < K < q.
6.9.4.2 Tạo tiền chữ ký
Đầu vào của bước này là số ngẫu nhiên K, và chủ thể ký tính
Π = [K]G.
6.9.4.3 Chuẩn bị thông điệp để ký
Thông điệp được chuẩn bị sao cho M1 là rỗng và M2 là thông điệp được ký, nghĩa là M2 = M.
6.9.4.4 Tính bằng chứng
Chủ thể ký tính R = FE2I(r, ΠX)mod q.
6.9.4.5 Tính nhiệm vụ
Chủ thể ký tính H = h(M2). H sau đó được biến đổi thành một số nguyên theo quy tắc biến đổi BS2I trong phụ lục B. Nếu H = 0 mod q, thì H được gán bằng 1. Nhiệm vụ (T1,T2) là (BS2I(γ,H),R), nếu BS2l(γ, H) ≠ 0(mod q), ngược lại là (1, R).
6.9.4.6 Tính toán thành phần thứ hai của chữ ký
Chữ ký (R,S) với R được tính như trong 6.9.4.4 và
S = RX + KH mod q.
Người ký kiểm tra xem R = 0 hoặc S = 0 hay không. Nếu một trong hai giá trị R hoặc S = 0, thì một giá trị mới của K được sinh ra và chữ ký được tính toán lại.
6.9.4.7 Xây dựng phần phụ lục
Phần phụ lục là phép ghép của (R,S) và một trường lựa chọn text, text, nghĩa là ((R,S)||text).
6.9.4.8 Xây dựng thông điệp đã ký
Một thông điệp đã ký là phép ghép, M, và phần phụ lục
M||((R,S) || text).
6.9.5 Tiến trình kiểm tra
6.9.5.1 Truy xuất bằng chứng
Người kiểm tra truy xuất bằng chứng R và thành phần thứ hai của chữ ký S từ phần phụ lục. Để kiểm tra xem 0 < R < q và 0 < S < q; nếu một trong các điều kiện đó bị vi phạm, chữ ký số sẽ bị từ chối.
6.9.5.2 Chuẩn bị thông điệp để kiểm tra
Người kiểm tra truy xuất M từ thông điệp đã ký và chia thông điệp thành hai phần M1 và M2. M1 là rỗng và M2 = M.
6.9.5.3 Truy xuất nhiệm vụ
Bước này giống với 6.9.4.5. Các đầu vào cho hàm nhiệm vụ bao gồm bằng chứng R từ 6.9.5.1 và M2 từ 6.9.5.2. Nhiệm vụ T = (T1,T2) được tính lại như là đầu ra của hàm nhiệm vụ 6.9.4.5.
6.9.5.4 Tính tại tiền chữ ký
Các đầu vào cho bước này là hệ thống các tham số, khóa kiểm tra Y, nhiệm vụ T = (T1,T2) từ 6.9.5.3 và thành phần thứ 2 của chữ ký số S từ 6.9.5.1. Người kiểm tra có được một giá trị tính lại Π' của tiền chữ ký dùng công thức:
Π' = [-T1-1T2mod q]Y + [T1-1S mod q]G.
6.9.5.5 Tính lại bằng chứng
Việc tính toán ở bước này giống như 6.9.4.4. Người kiểm tra thực hiện hàm bằng chứng. Đầu vào là Π' từ 6.9.5.4. Đầu ra là bằng chứng được tính lại R'
6.9.5.6 Kiểm tra bằng chứng
Người kiểm tra so sánh bằng chứng tính lại, R' từ 6.9.5.5 với giá trị của R từ 6.9.5.1. Nếu R' = R, thì chữ ký là hợp lệ.
6.10.1 Tổng quan
EC-SDSA (Thuật toán chữ ký số đường cong elliptic Schnorr) là cơ chế ký với khóa kiểm tra Y = [X]G; đó là, tham số D bằng 1. Thông điệp được chuẩn bị sao cho M2 là rỗng và M1 là thông điệp đã được ký, nghĩa là M1 = M. Bằng chứng R là mã băm của thông điệp M và một tiền chữ ký ngẫu nhiên Π = [K]G, bằng một trong hai phương pháp sau:
Thông thường R = h(FE2BS(r, ΠX) || FE2BS(r,Πγ) || M)
Hoặc
Được tối ưu R = h(FE2BS(r, ΠX)||M).
Phương pháp đầu tiên sinh ra bằng chứng bằng cách băm ghép nối tọa độ của Π theo trục x và trục y, và thông điệp M. Phương pháp thứ hai bỏ qua tọa độ y từ việc tính toán băm và qua đó nâng cao hiệu năng.
Phương pháp thứ hai là một biến thể tối ưu hóa của EC-SDSA (xem viện dẫn [30]).
Các hệ số (A, B, C) của EC-SDSA được thiết lập như sau
(A, B, C) = (T1,T2,S)
Với (T1,T2) = (-1,-BS2l(γ, R)mod q).
Vì vậy công thức ký trở thành
-K + T2X + S ≡ 0(mod q).
CHÚ THÍCH EC-SDSA viết tắt cho thuật toán chữ ký số đường cong elliptic Schnorr. Cơ chế này được lấy từ viện dẫn [33]. Các ký hiệu được thay đổi một chút so với viễn dẫn [33] để phù hợp với ký hiệu được dùng trong tiêu chuẩn này.
6.10.2 Các tham số
F một trường hữu hạn
E một nhóm đường cong elliptic trên trường F
#E lực lượng của E
q ước nguyên tố của #E
G một điểm trên đường cong elliptic bậc q
Định danh hàm băm hoặc OID với hàm băm được đặc tả.
Tất cả các tham số có thể được công khai và có thể dùng chung cho một nhóm người dùng.
Một khuyến nghị đối với toàn bộ người dùng kiểm tra việc sinh hợp lệ của các tham số công khai theo viện dẫn [7].
6.10.3 Sinh khóa ký và khóa kiểm tra
Khóa ký của một chủ thể ký là một số nguyên bí mật X được sinh giả ngẫu nhiên hoặc ngẫu nhiên sao cho 0 < X < q. Tham số D là 1. Tương ứng với khóa kiểm tra công khai Y là
Y = [X]G.
Một khóa ký bí mật X của người dùng và khóa kiểm tra công khai Y thường được cố định cho một chu kỳ thời gian. Khóa ký X được giữ bí mật.
6.10.4 Tiến trình ký
6.10.4.1 Tạo số ngẫu nhiên
Chủ thể ký tính toán một số nguyên K ngẫu nhiên hoặc giả ngẫu nhiên sao cho 0 < K < q.
6.10.4.2 Tạo tiền chữ ký
Đầu vào bước này là số nguyên ngẫu nhiên K, và chủ thể ký tính Π = [K]G.
6.10.4.3 Chuẩn bị thông điệp để ký
Thông điệp được chuẩn bị sao cho M1 là thông điệp được ký, nghĩa là M1 = M, và M2 là rỗng.
6.10.4.4 Tính bằng chứng
Chủ thể ký tính R = h(FE2BS(r, ΠX)||FE2BS(r,ΠY)||M).
Để tối ưu hóa biến thể của EC-SDSA, chủ thể ký tính R = h(FE2BS(r,ΠX)||M).
6.10.4.5 Tính nhiệm vụ
Giá trị của bằng chứng R được biến đổi thành một số nguyên theo quy tắc biến đổi BS2I, trong phụ lục B và rút gọn theo modulo q.
Nhiệm vụ (T1,T2) là (-1,-BS2I(γ,R)mod q).
6.10.4.6 Tính toán phần thứ hai của chữ ký số
Chữ ký (R,S) với S = (K + BS2I(γ, R)X)mod q).
Như một sự lựa chọn, một mong muốn để kiểm tra nếu R = 0 hoặc S = 0. Nếu một trong hai giá trị R = 0 hoặc S = 0, một giá trị mới của K được sinh ra và chữ ký được tính toán lại (rất hiếm khi xảy ra R = 0 hoặc S = 0 nếu chữ ký số được sinh đúng).
6.10.4.7 Xây dựng phần phụ lục
Phần phụ lục là phép ghép của (R,S) và một trường lựa chọn text, text.
6.10.4.8 Xây dựng thông điệp đã ký
Một thông điệp đã ký là phép ghép thông điệp M và phần phụ lục.
M||((R,S)||text).
6.10.5 Tiến trình kiểm tra
6.10.5.1 Tổng quan
Chủ thể kiểm tra yêu cầu các dữ liệu cần thiết được yêu cầu cho tiến trình kiểm tra.
6.10.5.2 Truy xuất bằng chứng
Người kiểm tra truy xuất bằng chứng R và thành phần thứ hai của chữ ký S từ phần phụ lục. Người kiểm tra kiểm tra xem R là một xâu khác 0 trong dải của hàm băm hay không và 0 < S < q. Nếu một trong các điều kiện đó bị vi phạm, chữ ký số sẽ bị từ chối.
6.10.5.3 Chuẩn bị thông điệp để kiểm tra
Người kiểm tra truy xuất M từ thông điệp đã ký và chia thông điệp thành hai phần M1 và M2. M2 là rỗng và M1 = M.
6.10.5.4 Truy xuất nhiệm vụ
Đầu vào của hàm nhiệm vụ bao gồm bằng chứng R từ 6.10.5.2. Nhiệm vụ T = (T1,T2) = (-1, -BS2I(γ, R)mod q).
6.10.5.5 Tính lại tiền chữ ký
Các đầu vào cho bước này là hệ thống các tham số, khóa kiểm tra Y, nhiệm vụ T = (T1,T2) từ 6.10.5.4 và thành phần thứ 2 của chữ ký số S từ 6.10.5.2. Người kiểm tra có được một giá trị tính lại Π' của tiền chữ ký dùng công thức:
Π' = [-ST1mod q]G + [T2 mod q]Y = [S mod q]G + [T2 mod q]Y.
6.10.5.6 Tính lại bằng chứng
Việc tính toán ở bước này giống như 6.10.4.4 và 6.10.4.5. Người kiểm tra thực hiện hàm bằng chứng từ 6.10.4.4. Đầu vào là Π' từ 6.10.5.5. Đầu ra là bằng chứng được tính lại R' là mã băm của tiền chữ ký được tính lại Π' và thông điệp M.
6.10.5.7 Kiểm tra bằng chứng
Người kiểm tra so sánh bằng chứng tính lại, R' từ 6.10.5.6 với giá trị của R từ 6.10.5.2. Nếu R' = R, thì chữ ký là hợp lệ.
6.11.1 Tổng quan
EC-FSDSA (Thuật toán chữ ký số đường cong elliptic Schnorr đầy đủ) là cơ chế chữ ký số với khóa kiểm tra Y = [X]G; tham số D bằng 1. Thông điệp được chuẩn bị sao cho M1 là rỗng và M2 = M là thông điệp được ký. Bằng chứng R được tính như sau:
R = FE2BS(r,ΠX)||FE2BS(r, ΠY).
Các hệ số (A, B, C) của công thức chữ ký EC-FSDSA được thiết lập như sau:
(A, B, C) = (T1,T2,S).
Với T = (T1,T2) = (-1,-BS2I(γ,h(R || M))mod q).
Vì vậy, công thức ký sẽ là:
-K + T2X + S ≡ 0(mod q)
CHÚ THÍCH EC-SDSA viết tắt cho thuật toán chữ ký số đường cong elliptic Schnorr đầy đủ. Cơ chế này được lấy từ viện dẫn [33]. Các ký hiệu được thay đổi một chút so với viễn dẫn [33] để phù hợp với ký hiệu được dùng trong tiêu chuẩn này.
6.11.2 Các tham số
F một trường hữu hạn
E một nhóm đường cong elliptic trên trường F
#E lực lượng của E
q ước nguyên tố của #E
G một điểm trên đường cong elliptic bậc q
Định danh hàm băm hoặc OID với hàm băm được đặc tả.
Tất cả các tham số có thể được công khai và có thể dùng chung cho một nhóm người dùng.
Một khuyến nghị đối với toàn bộ người dùng kiểm tra việc sinh hợp lệ của các tham số công khai theo viện dẫn [7].
6.11.3 Sinh khóa ký và khóa kiểm tra
Khóa ký của một chủ thể ký là một số nguyên bí mật X được sinh giả ngẫu nhiên hoặc ngẫu nhiên sao cho 0 < X < q. Tham số D là 1. Tương ứng với khóa kiểm tra công khai Y là
Y = [X]G.
Một khóa ký bí mật X của người dùng và khóa kiểm tra công khai Y thường được cố định cho một chu kỳ thời gian. Khóa ký X được giữ bí mật.
6.11.4 Tiến trình ký
6.11.4.1 Tạo số ngẫu nhiên
Chủ thể ký tính toán một số nguyên ngẫu nhiên hoặc giả ngẫu nhiên K sao cho 0 < K < q.
6.11.4.2 Tạo tiền chữ ký
Đầu vào bước này là số ngẫu nhiên K, và chủ thể ký tính Π = [K]G.
6.11.4.3 Chuẩn bị thông điệp để ký
Thông điệp được chuẩn bị sao cho M là thông điệp được ký, nghĩa là M2 = M, và M1 là rỗng.
6.11.4.4 Tính bằng chứng
Chủ thể ký tính R = FE2BS(r, ΠX)||FE2BS(r,ΠY).
6.11.4.5 Tính nhiệm vụ
Chủ thể ký tính mã băm h(R||M). Sau đó, hàm băm được biến đổi thành một số nguyên theo quy tắc biến đổi, BS2I, trong phụ lục B và sau đó được rút gọn theo modulo q. Nhiệm vụ (T1,T2) là (-1,-BS2I(γ, h(R||M))mod q).
6.11.4.6 Tính toán thành phần thứ hai của chữ ký
Chữ ký (R, S) với S = (K + BS2l(γ, h(R || M))Xmod q).
Như một sự lựa chọn, một mong muốn để kiểm tra nếu R = 0 hoặc S = 0. Nếu một trong hai giá trị R = 0 hoặc S = 0, một giá trị mới của K được sinh ra và chữ ký được tính toán lại (rất hiếm khi xảy ra R = 0 hoặc S = 0 nếu chữ ký số được sinh đúng).
6.11.4.7 Xây dựng phần phụ lục
Phần phụ lục là phép ghép của (R, S) và một trường lựa chọn text, text.
6.11.4.8 Xây dựng thông điệp đã ký
Một thông điệp đã ký là phép ghép của thông điệp M và phần phụ lục
M||((R,S)||text)
6.11.5 Tiến trình kiểm tra
6.11.5.1 Tổng quan
Chủ thể kiểm tra yêu cầu các dữ liệu cần thiết được yêu cầu cho quá trình kiểm tra.
6.11.5.2 Truy xuất bằng chứng
Người kiểm tra truy xuất bằng chứng R và thành phần thứ hai của chữ ký S từ phần phụ lục. Người kiểm tra kiểm tra xem R là một xâu khác 0 trong dải của hàm băm hay không và 0 < S < q. Nếu một trong các điều kiện đó bị vi phạm, chữ ký số sẽ bị từ chối.
6.11.5.3 Chuẩn bị thông điệp để kiểm tra
Người kiểm tra truy xuất M từ thông điệp đã ký và chia thông điệp thành hai phần M1 và M2, sao cho M2 = M và M1 là rỗng.
6.11.5.4 Truy xuất nhiệm vụ
Đầu vào của hàm nhiệm vụ được tính như trong 6.11.4.5 từ bằng chứng R từ 6.11.4.4 và thông điệp M từ 6.11.4.3. Nhiệm vụ được đưa ra bởi T = (T1,T2) = (-1,-BS2l(γ, h(R || M))mod q).
6.11.5.5 Tính lại tiền chữ ký
Các đầu vào cho bước này là hệ thống các tham số, khóa kiểm tra Y, nhiệm vụ T = (T1,T2) từ 6.11.5.4 và thành phần thứ 2 của chữ ký số S từ 6.11.5.2. Người kiểm tra có được một giá trị tính lại Π' của tiền chữ ký dùng công thức:
Π'=[-ST1mod q]G+[T2mod q]Y=[S mod q]G + [T2mod q]Y.
6.11.5.6 Tính lại bằng chứng
Việc tính toán ở bước này giống như 6.11.4.4. Người kiểm tra thực hiện hàm bằng chứng. Đầu vào là Π' từ 6.11.5.5. Đầu ra được tính lại là bằng chứng R’.
6.11.5.7 Kiểm tra bằng chứng
Người kiểm tra so sánh bằng chứng tính lại, R' từ 6.11.5.6 với giá trị của R từ 6.11.5.2. Nếu R' = R, thì chữ ký là hợp lệ
7 Các cơ chế dựa trên định danh
Các dữ liệu được yêu cầu cho tiến trình ký như sau:
- Các tham số miền, E, GF(r), G1, G2, q, p, <>;
- Khóa chủ công khai V;
- Khóa ký X;
- Thông điệp M;
- Định danh hàm băm cho H1 và H2 (tùy chọn);
- Xâu định danh ID;
- Ký tự khác (tùy chọn)
Định danh hàm băm có thể được sử dụng đề che giấu cơ chế ký và hàm băm. Các dữ liệu được yêu cầu cho tiến trình kiểm tra như sau:
- Các tham số miền, E, GF(r), G1, G2, q, P, <>;
- Khóa chủ công khai V:
- Khóa kiểm tra Y, có thể được dẫn xuất từ một xâu định danh;
- Thông điệp M;
- Chữ ký Σ;
- Định danh hàm băm cho H1 và H2 (tùy chọn);
CHÚ THÍCH 1 Người ký và người kiểm tra phải thống nhất về các hàm băm cụ thể cho h, H1 và H2 được dùng trong cơ chế. Nếu không xác định được hàm băm, thì hàm băm định danh được yêu cầu sử dụng cho cả tiến trình ký và tiến trình kiểm tra (xem TCVN 12214-1 (ISO/IEC 14888-1)).
- Xâu định danh ID;
- Ký tự khác (tùy chọn).
CHÚ THÍCH 2 Các đường cong elliptic điển hình cho IBS-1 và IBS-2 là các đường cong elliptic siêu kỳ dị trên GF(r), trong đó r = pm, p là số nguyên tố ≥ 2 và m là số nguyên ≥ 1.
7.2.1 Tổng quan
IBS-1 là một lược đồ ký dựa trên định danh trên một nhóm cộng của các điểm trên đường cong elliptic.
Ta có:
(A, B, C) = (T1,S,T2)
Trong đó T1 = -Y,T2 =[R]Y.D = -1. Do đó, công thức ký biến đổi thành:
[-K]Y + [U-1]S + [R]Y ≡ 0E (trong G1).
CHÚ THÍCH Cơ chế này dựa trên thuật toán được thiết kế bởi Hess trong viện dẫn [22],
7.2.2 Các tham số
Cơ chế ký được thực hiện trong trường hợp các thực thể tham gia chia sẻ các tham số được xác định trong Điều 4 như sau: G1,G2,P,q,<>,H1 và H2.
Một khuyến nghị đối với toàn bộ người dùng kiểm tra việc sinh hợp lệ của các tham số công khai.
7.2.3 Sinh khóa chủ và khóa ký/kiểm tra
Cặp khóa chủ của KGC là (U, V), trong đó U là khóa chủ riêng được sinh ra bằng cách lựa chọn một số nguyên ngẫu nhiên sao cho 0 < U < q và V là khóa chủ công khai được sinh ra bằng cách tính V = [U]P. KGC công khai V và giữ bí mật U.
Cặp khóa ký và kiểm tra của người ký là (X, Y), trong đó Y là khóa kiểm tra công khai được sinh ra từ một xâu định danh ID và hàm băm H1, tức là Y = H1(ID) và X là khóa ký riêng được sinh ra bằng cách tính X = [U]Y, do KGC thực hiện và gửi cho người ký.
7.2.4 Tiến trình ký
7.2.4.1 Tạo số ngẫu nhiên
Trước tiên người ký lựa chọn ngẫu nhiên hoặc giả ngẫu một số nguyên K nhiên sao cho 0 < K < q. Người ký giữ bí mật giá trị K.
7.2.4.2 Tạo tiền chữ ký
Người ký lấy đầu vào là K, P và X để tạo ra tiền chữ ký.
Π =< X, P >K.
CHÚ THÍCH Π là một phần tử trên một trường mở rộng của GF(pm) và phần mở rộng bậc 4 với p = 2, bậc 6 với p = 3 và bậc 2 với p > 3.
7.2.4.3 Chuẩn bị thông điệp để ký
Người ký chuẩn bị thông điệp ký sao cho M2 là rỗng và M1 là thông điệp được ký, tức là M1 = M.
7.2.4.4 Tính bằng chứng
Đặt Π = (Πa, Πb). Người ký sử dụng hàm băm H2 cho M1 || FE2BS(r, Πa) || FE2BS(r, Πb) (Phép ghép của M1 và FE2BS(r, Πa) và FE2BS(r, Πb)) để thu được bằng chứng.
R = BS2I(γ, H2(M1 || FE2BS(r, Πa) || FE2BS(r, Πb)))mod q.
Nếu R = 0, thì đầu ra là không hợp lệ và dừng.
Đối với các trường có bậc mở rộng cao hơn, sẽ có nhiều thành phần xuất hiện trong giá trị được băm. Ví dụ, đối với bậc mở rộng 3, Π = (Πa, Πb, Πc) và đầu vào của H2 có thể là:
M1 || FE2BS(r, Πa) || FE2BS(r, Πb) || FE2BS(r, Πc).
7.2.4.5 Tính nhiệm vụ
Nhiệm vụ T = (T1,T2) hoặc (-Y, [R]Y). Tuy nhiên, người ký không cần tính nhiệm vụ.
7.2.4.6 Tính toán phân thứ hai của chữ ký
Người ký tính toán phần thứ hai của chữ ký như sau:
S = [K- R]X.
Chữ ký là Σ = (R,S).
7.2.4.7 Xây dựng phần phụ lục
Phần phụ lục được xây dựng bởi người ký là phép ghép của (R,S) với một trường text tùy chọn ((R,S), text).
7.2.4.8 Xây dựng thông điệp đã ký
Một thông điệp đã ký là phép ghép của thông điệp M và phần phụ lục
M || ((R,S) || text)
7.2.5 Tiến trình kiểm tra
7.2.5.1 Tổng quan
Chủ thể kiểm tra yêu cầu các dữ liệu cần thiết cho tiến trình kiểm tra.
7.2.5.2 Truy xuất bằng chứng
Người kiểm tra truy xuất bằng chứng R và thành phần thứ hai của chữ ký S từ phần phụ lục và kiểm tra xem S ϵ G1 hay không; Nếu điều kiện này bị vi phạm, chữ ký số sẽ bị từ chối. Ngược lại, người kiểm tra sẽ thực hiện các bước sau.
7.2.5.3 Chuẩn bị thông điệp để kiểm tra
Người kiểm tra truy xuất M từ thông điệp đã ký và chia thông điệp thành hai phần M1 và M2, sao cho M1 = M và M2 là rỗng.
7.2.5.4 Truy xuất nhiệm vụ
Nhiệm vụ T = (T1,T2) trong đó T1 = -Y và T2 = [R]Y. Tuy nhiên, người kiểm tra không cần tính nhiệm vụ.
7.2.5.5 Tính lại tiền chữ ký
Người kiểm tra tính lại giá trị tiền chữ ký
Π' =< S, P >*< Y, V >R.
CHÚ THÍCH Cặp < Y,V > có thể tính toán trước.
7.2.5.6 Tính lại bằng chứng
Người kiểm tra tính lại bằng chứng
R' = BS2l(γ, H2(M1 || FE2BS(r, Π'a) || FE2BS(r, Π'b)))mod q
Đối với các trường có bậc mở rộng cao hơn, sẽ có nhiều thành phần xuất hiện trong giá trị được băm. Ví dụ, đối với bậc mở rộng 3, Π' = (Π'a, Π'b, Π'c) và đầu vào của H2 có thể là:
M1 || FE2BS(r, Π'a) || FE2BS(r, Π'b) || FE2BS(r, Π'c).
7.2.5.7 Kiểm tra bằng chứng
Người kiểm tra so sánh R' = R hay không. Nếu bằng thì chữ ký được kiểm tra, ngược lại chữ ký là không hợp lệ
7.3.1 Tổng quan
IBS-2 là một lược đồ ký dựa trên định danh trên một nhóm cộng của các điểm trên đường cong elliptic. Ta có:
(A, B, C) = (T1,S,T2)
Trong đó T1 = -Y,T2 = [-H]Y và H là một mã băm từ H2. D = -1.
Do đó, công thức chữ ký là:
[-K]Y + [U-1]S + [-H]Y ≡ 0E(trong G1).
CHÚ THÍCH Cơ chế này dựa trên thuật toán được thiết kế bởi Hess trong viện dẫn [15].
7.3.2 Các tham số
Các tham số giống như Điều 7.2.2.
7.3.3 Sinh khóa chủ và khóa ký/kiểm tra
Quá trình này giống như Điều 7.2.3.
7.3.4 Tiến trình ký
7.3.4.1 Tạo số ngẫu nhiên
Trước tiên người ký lựa chọn ngẫu nhiên hoặc giả ngẫu một số nguyên K nhiên sao cho 0 < K < q. Người ký giữ bí mật giá trị K.
7.3.4.2 Tạo tiền chữ ký
Người ký lấy đầu vào là K, P và X để tạo ra tiền chữ ký.
Π = [K]Y.
7.3.4.3 Chuẩn bị thông điệp để ký
Người ký chuẩn bị thông điệp ký sao cho M1 là rỗng và M2 là thông điệp được ký, tức là M2 = M.
7.3.4.4 Tính bằng chứng
Chủ thể ký nhận được bằng chứng từ kết quả tiền chữ ký
R = Π.
7.3.4.5 Tính nhiệm vụ
Nhiệm vụ T = (T1,T2) trong đó:
T1 = -Y, và
T2 = [-H]Y
Trong đó H = BS2I(γ, H2(M2||FE2BS(r, ΠX))) mod q. Tuy nhiên, người ký chỉ cần tính toán giá trị H.
7.3.4.6 Tính toán phần thứ hai của chữ ký
Người ký tính toán phần thứ hai của chữ ký như sau:
S = [K + H]X.
Chữ ký là Σ = (R, S).
7.3.4.7 Xây dựng phần phụ lục
Phần phụ lục được xây dựng bởi người ký là phép ghép của (R,S) với một trường text tùy chọn ((R,S), text)
7.3.4.8 Xây dựng thông điệp được ký
Một thông điệp đã ký là phép ghép của thông điệp M và phần phụ lục, tức là
M || ((R, S) || text).
7.3.5 Tiến trình kiểm tra
7.3.5.1 Tổng quan
Chủ thể kiểm tra yêu cầu các dữ liệu cần thiết cho tiến trình kiểm tra.
7.3.5.2 Truy xuất bằng chứng
Người kiểm tra truy xuất tiền chữ ký R và thành phần thứ hai của chữ ký S từ phần phụ lục. Trước tiên, người kiểm tra kiểm tra xem S ϵ G1 hay không; Nếu điều kiện này bị vi phạm, chữ ký số sẽ bị từ chối. Ngược lại, người kiểm tra sẽ thực hiện các bước sau.
7.3.5.3 Chuẩn bị thông điệp để kiểm tra
Người kiểm tra truy xuất M từ thông điệp đã ký và chia thông điệp thành hai phần M1 và M2, sao cho M2 = M và M1 là rỗng.
7.3.5.4 Truy xuất nhiệm vụ
Nhiệm vụ T = (T1,T2) trong đó:
T1 = -Y, và
T2 = [-H]Y
Trong đó H = BS2I(γ, H2(M2 || FE2BS(r, ΠX)))mod q. Tuy nhiên, người kiểm tra chỉ cần tính toán lại giá trị H.
7.3.5.5 Tính lại tiền chữ ký
Người kiểm tra truy xuất giá trị tiền chữ ký là:
Π' = R.
7.3.5.6 Tính toán lại bằng chứng
Thay bằng việc tính toán lại giá trị bằng chứng R, người kiểm tra tính toán hai cập < P, S > và < V, Π' + [H]Y >.
7.3.5.7 Kiểm tra bằng chứng
Người kiểm tra kiểm tra xem < P, S >=< V, Π' + [H]Y > hay không. Nếu thỏa mãn điều kiện thì chữ ký được h; ngược lại, chữ ký không hợp lệ.
Thư mục tài liệu tham khảo
[1] TCVN 7817-3 Công nghệ thông tin - Các Kỹ thuật an toàn - Quản lý khóa - Phần 3: Các cơ chế sử dụng kỹ thuật phi đối xứng.
[2] TCVN 11367-3, Công nghệ thông tin - Các kỹ thuật an toàn - Thuật toán mật mã - Phần 2: Mật mã phi đối xứng
[3] ISO/IEC 15945:2002, Information technology - Security techniques - Specification of TTP services to support the application of digital signatures
[4] ISO/IEC 15946-1:2008, Information technology - Security techniques - Cryptographic techniques based on elliptic curves - Part 1: General
[5] ISO/IEC 18032:2005, Information technology - Security techniques - Prime number generation
[6] ISO/IEC 9594-8:2001 I ITU-T Rec. X.509 (2002 E), Information technology - Open Systems Interconnection - The Directory: Public-key and attribute certificate frameworks
[7] American National Standards Institute, Public Key Cryptography for the Financial Services Industry: The Elliptic Curve Digital Signature Algorithm (ECDSA), ANSI X9.62-2005, 2005
(81 BARRETO P., KIM H., LYNN B., SCOTT M. Efficient algorithms for pairing-based cryptosystems, Proceedings of CRYPTO 2002, LNCS 2442, pages 354-369, Springer-Verlag, 2002
[9] BELLARE M., GARAY J., RABIN T. Fast Batch Verification for Modular Exponentiation and Digital Signatures, Advances in Cryptology - Eurocrypt 98 Proceedings, LCNS, Vol. 1403, pp. 236-250, Springer-Verlag, 1998
[10] BOHLI J.M., ROHRICH S., STEINWANDT R. Key substitution attacks revisited: taking into account malicious signers. Int. J. Inf. Secur. 2006, 5 pp. 30-36
[11] BONEIT D., & FRANKLIN M. Identity based encryption from the Weil pairing, Proceedings of CRYPTO 2001, LNCS 2139, pp. 213-229, Springer-Verlag, 2001
[12] BRICKELL E., POINTCHEVAL D., VAUDENAY S., YUNG M. Design Validations for Discrete Logarithm Based Signature Schemes, Proceedings of PKC 2000, LNCS 1751, pp. 276-292, Springer- Verlag, 2000
[13] BROWN D.R.L. Generic Groups, Collision Resistance, and ECDSA. Des. Codes Cryptogr., 35 (1) pp. 119-152
[14] BROWN D.R.L. In: On the Provable Security of ECDSA, "Advances in Elliptic Curves ryptography. (BLAKE I., SEROUSSI G., SMART N. eds.). Cambridge University Press, Chapter II. 2005
[15] CHA J.C., & CHEON J.H. An identity-based signature from gap Diffie-Hellman groups, Proceedings of PKC 2002, LNCS 2567, pp. 18-30, Springer-Verlag, 2002
[16] ERWIN H., & PASCALE S. Digital Signature Scheme EC-GDSA, German Federal Office for Information Security, December 2005
[17] FIPS PUB 186-4, Digital Signature Standard (DSS). U.S. National Institute of Standards and Technology, Gaithersburg, Maryland, 2013
[18] FREY G., MULLER M., ROCK H. The Tate pairing and the discrete logarithm applied to elliptic curve cryptosystems. IEEE Trans. Inf. Theory. 1999, 45 (5) pp. 1717-1719
[19] GALBRAITH S. Supersingular curves in cryptography, Proceedings of Asiacrypt 2001, LNCS 2248. Springer-Verlag, 2001, pp. 495-513 130 ISO/IEC 2016 - All rights reservedlSO/IEC 14888-3:2016(E)
[20] GALBRAITH S., HARRISON K., SOLDERA D. Implementing the Tate-pairing, Proceedings of ANTS- V, LNCS 2369, pp. 324-337, Springer-Verlag, 2002
[21] GOST R 34.10-2012, State Standard of the Russian Federation, "Information technology Cryptographic data security Signature and verification processes of [electronic] digital signature." State Committee of the Russian Federation on Standards and Metrology, 2012. (In Russian)
[22] HESS F. Efficient identity based signature schemes based on pairings, Proceedings of SAC 2002, 2002
[23] IEEE P1363, Standard Specifications for public key cryptography
[24] KOBLITZ N. Elliptic Curve Cryptosystems. Math. Comput. 1987, 48 pp. 203-209
[25] LENSTRA A.K., & VERHEUL E.R. Selecting cryptographic key sizes, in Journal of Cryptology, Vol. 14-4, pp. 255-293, 2001
[26] MENEZES A. Elliptic Curve Public Key Cryptosystems. Kluwer Academic Publishers, 1993
[27] MENEZES A.J., OKAMOTO T., VANSTONE S. Reducing elliptic curve logarithms to logarithms in a finite field. IEEE Trans. Inf. Theory. 1993, 39 pp. 1639-1646
[28] MILLER V.S. Use of Elliptic Curves in Cryptology, Proceedings of Crypto 1985, H.C. Williams, Ed., LNCS 218, pp. 417-426, Berlin, Springer-Verlag, 1986
[29] MILLER V. The Weil pairing, and its efficient calculation, Journal of Cryptology, Vol. 17-4, pp. 235-261, 2004
[30] NEVEN G., SMART N., WARINSCHI B. Hash function requirements for Schnorr signatures. Journal of Mathematical Cryptology. 2009, 3 pp. 69-87
[31] POINTCHEVAL D., & VAUDENAY s. On provable security for digital signature algorithms, Technical Report LIENS-96-17, LIENS, 1996
[32] SCHNORR C.P. Efficient identification and signature for smart cards. In Advances in Cryptology Crypto’89, LNCS 435, pp.239-252, Springer-Veriag, 1990
[33] SCHNORR C.P. Efficient signature generation for smart cards. J. Cryptol. 1991,4 pp. 161-174
[34] SILVERMAN R. A cost-based security analysis of symmetric and asymmetric key lengths, RSA Labs Bulletin, Vol. 13, April 2000 (revised November 2001)
[35] SILVERMAN J.H. Advanced topics in the arithmetic of elliptic curves, GTM 151. SpringerVerlag, 1994
[36] TTAK.KO-12.0001/R3, Digital Signature Mechanism with Appendix - Part 2: Korean Certificatebased Digital Signature Algorithm KCDSA, 2014. (In Korean)
[37] TTAK.KO-12.0015/R2, Digital Signature Mechanism with Appendix - Part 3: Korean Certificatebased Digitial Signature Algorithm using Elliptic Curves EC-KCDSA, 2014. (In Korean)
[38] VARNOVSKII N.P. Provable security of digital signatures in the tamper-proof device model. Discrete Math. Appl. 2008, 18 (4) pp. 427-437
[39] VAUDENAY S. Hidden Collisions on DSS, Proceedings of CRYPTO 1996, LNCS 1109, pp. 83-88, Springer-Verlag, 1996
[40] YEN S., & LAIH C. Improved Digital Signature Suitable for Batch Verification. IEEE Trans. Comput. 1995, 44 (7) pp. 957-959
[41] YUM D.H., & LEE P.J. Security Proof for KCDSA under the Random Oracle Model. Proceedings of CISC. 1999, 1999 pp. 173-180


