Manipulating industrial robots - Informative guide on test equipment and metrology methods of operation for robot performance evaluation in accordance with ISO 9283
Lời nói đầu
TCVN 13699:2023 hoàn toàn tương đương ISO TR 13309:1995
TCVN 13699:2023 do Ban kỹ thuật tiêu chuẩn quốc gia TCVN/TC 299, Robot biên soạn, Tổng cục Tiêu chuẩn Đo lường Chất lượng đề nghị, Bộ Khoa học và Công nghệ công bố.
TAY MÁY RÔ BỐT CÔNG NGHIỆP - HƯỚNG DẪN VỀ THIẾT BỊ THỬ VÀ CÁC PHƯƠNG PHÁP ĐO TRONG VẬN HÀNH ĐỂ ĐÁNH GIÁ TÍNH NĂNG CỦA RÔ BỐT PHÙ HỢP VỚI TCVN 13696 (ISO 9283)
Manipulating industrial robots - Informative guide on test equipment and metrology methods of operation for robot performance evaluation in accordance with ISO 9283
Tiêu chuẩn này cung cấp thông tin về trình độ phát triển khoa học - kỹ thuật của các nguyên lý vận hành thiết bị thử. Thông tin bổ sung được cung cấp sẽ mô tả các ứng dụng của công nghệ hiện nay về thiết bị thử theo TCVN 13696 (ISO 9283).
2 Các loại phương pháp đo đặc tính chủ yếu
Có một số phương pháp được sử dụng để mô tả đặc điểm các tính năng của rô bốt phù hợp TCVN 13696 (ISO 9283). Các phương pháp này được phân loại như sau:
1. Các phương pháp xác định vị trí bằng đầu dò
2. Các phương pháp so sánh quỹ đạo
3. Các phương pháp đo ba cạnh tam giác
4. Các phương pháp đo tọa độ cực
5. Phương pháp tam giác đạc
6. Phương pháp đo quán tính
7. Các phương pháp đo tọa độ
8. Phương pháp vẽ quỹ đạo
Thảo luận ngắn về các phương pháp này được cho trong Điều 4. Có thể tìm thấy mô tả chi tiết về các hệ thống này trong các tài liệu được cho trong mục Tài liệu tham khảo (Phụ lục C).
3 Các phương pháp đo đặc tính của rô bốt được khuyến nghị
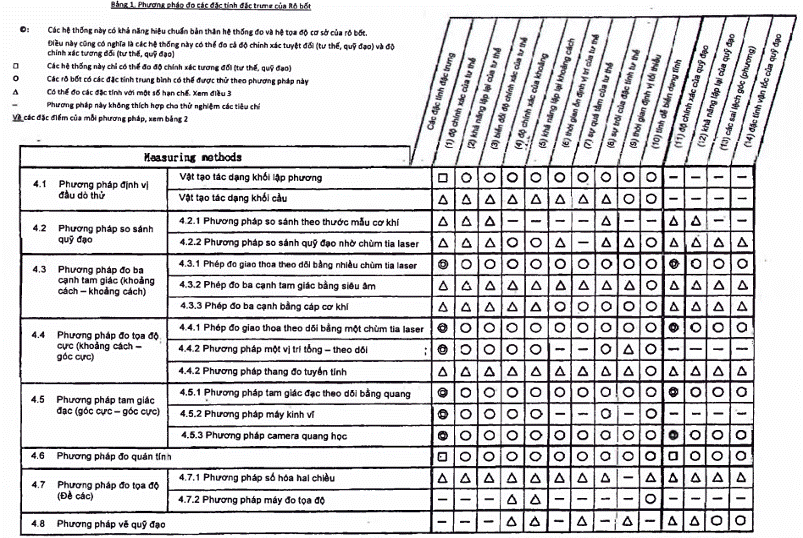
Bảng 1 giới thiệu bản kê các phương pháp được khuyến nghị để đo các tiêu chí đặc tính phù hợp với TCVN 13696 (ISO 9283). Các phương pháp đã phân loại thành tám loại trong Điều 2 được ghi theo từng khoản thành tổng số 16 phương pháp riêng. Các khả năng của mỗi phương pháp cũng được đưa ra. Mặc dù có thể sử dụng một số phương pháp để đo các đặc tính của cả tư thế và quỹ đạo nhưng một số phương pháp có các giới hạn. Các giới hạn đó là:
- (1) Chỉ có thể đo vị trí (hoặc hướng) trong thử nghiệm đặc tính tư thế.
- (2) Chỉ có thể đo các đặc tính của quỹ đạo (đường thẳng hoặc đường tròn) dọc theo các quỹ đạo điều khiển bị giới hạn.
- (3) Chỉ có thể thử nghiệm các rô bốt có quá tầm bị giới hạn
- (4) Đặc tính của thiết bị thử không thể cung cấp đủ độ chính xác hoặc độ không ổn định đo các đặc tính đặc biệt.
- (5) Phép đo được giới hạn cho số bậc tự do của thiết bị thử.
- (6) Thiết bị thử có thể cung cấp thể tích đo có giới hạn so với khối lập phương thử được định nghĩa trong ISO 9283.
- (7) Tần suất lấy mẫu của thiết bị thử không thể khớp với tần số đỉnh của chuyển động rô bốt được đo.
Người thử nghiệm nên thảo luận các giới hạn với nhà sản xuất thiết bị thử trước khi lập kế hoạch đo đặc tính.
Bảng 2 giới thiệu tóm tắt các đặc tính đặc trưng điển hình và các khả năng của các phương pháp được khuyến nghị sử dụng, cần lưu ý rằng trước khi thử nghiệm một rô bốt, người thử nghiệm nên hiểu rõ các mức đặc tính của rô bốt và lựa chọn các phương pháp thử thích hợp.
4 Các phương pháp đo đặc tính của rô bốt
Điều này đưa ra sự mô tả và các cấu hình dạng sơ đồ của các phương pháp được liệt kê trong Bảng 1.
4.1 Các phương pháp xác định vị trí bằng đầu dò
Có thể đo các đặc tính đạt được của tư thế khi sử dụng một đầu dò có chứa đủ số lượng các bộ cảm biến dịch chuyển hoặc các bộ cảm biến tiếp cận được vị trí bởi rô bốt để tiếp xúc chậm một vật mẫu chính xác được đặt tại một vị trí quy định hoặc ở lại trong không khí để đo quá tầm có thể có. Hình 1 giới thiệu một thiết bị điển hình. Hình 2 giới thiệu một số dạng mẫu và đầu dò. Một vài kiểu vật mẫu và các đầu dò có thể được kết hợp với nhau tùy thuộc vào số lượng các thông số của tư thế được yêu cầu.

Hình 1 - Phương pháp xác định vị trí bằng dầu dò
(vật mẫu dạng khối lập phương)

Hình 2 - Các vật mẫu của phương pháp xác định vị trí bằng đầu dò
4.2 Các phương pháp so sánh quỹ đạo (đường dẫn)
4.2.1 So sánh theo căn mẫu cơ khí
Các phương pháp này dựa trên so sánh một quỹ đạo đạt được với một quỹ đạo yêu cầu có thể gồm có các đoạn thẳng hoặc các đoạn quỹ đạo tròn. Quỹ đạo được thiết kế trên cơ sở sử dụng căn mẫu cơ khí chính xác hoặc cấu trúc tham chiếu vị trí khác. Hình 3 giới thiệu một thiết bị dùng cho phương pháp trong đó các bộ cảm biến tiếp cận được lắp trên đầu dò dạng khối lập phương và vật mẫu có một cạnh thẳng biểu thị quỹ đạo điều khiển. Các sai lệch xuất hiện trong quá trình thực hiện quỹ đạo được cảm biến bởi số lượng thích hợp các bộ cảm biến và được sử dụng để xác định các thông số đặc tính (độ chính xác và khả năng lặp lại) của quỹ đạo đạt được. Toàn bộ các sai lệch của tư thế (vị trí và định hướng) cũng có thể được xác định khi sử dụng đủ các bộ cảm biến.
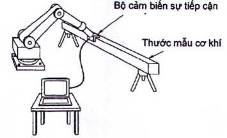
Hình 3 - So sánh với căn mẫu cơ khí
4.2.2 So sánh quỹ đạo sử dụng chùm tia la ser
Có thể đo độ chính xác/ khả năng lặp lại của quỹ đạo dọc theo một chùm tia laser với bộ cảm biến quang có khả năng phát hiện sai số vị trí của chùm tia tới từ tâm. Hệ thống thiết bị được giới thiệu trên Hình 4.
Có thể tính toán xác định tư thế của rô bốt dọc theo chùm tia là một hàm số của thời gian nếu nguồn laser được thay thế bằng một giao thoa kế laser và cảm biến quang có khả năng phản xạ ánh sáng.
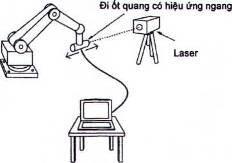
Hình 4 - So sánh quỹ đạo sử dụng chùm tia laser
4.3 Các phương pháp đo ba cạnh tam giác
Đo ba cạnh tam giác (có nghĩa là “sử dụng ba cạnh”) là một phương pháp xác định tọa độ Đề các (X,Y,Z) của một điểm P trong không gian ba chiều với ba giá trị khoảng cách giữa điểm P và ba vị trí quan sát, và các chiều dài cơ sở giữa ba vị trí cố định. Hình 5 giải thích nguyên lý của phép đo ba cạnh tam giác được biểu diễn theo hai chiều.

Hình 5 - Nguyên lý đo ba cạnh tam giác
4.3.1 Phép đo giao thoa bằng nhiều chùm tia laser
Phương pháp này dựa trên cơ sở sử dụng ba chùm tia laser được phát ra từ ba giao thoa kế laser được điều khiển servo theo hai trục nhằm bám theo một bia chung được bố trí trên cổ tay rô bốt. Hệ thống thiết bị được giới thiệu trên Hình 6. Có thể xác định đặc tính tư thế của rô bốt trong không gian ba chiều dựa trên các dữ liệu về khoảng cách thu được từ ba giao thoa kế. Có thể đo được hướng (định hướng) nếu sử dụng sáu giao thoa kế trong một thiết bị, trong đó sáu chùm tia được nhằm vào ba bia độc lập trên rô bốt.
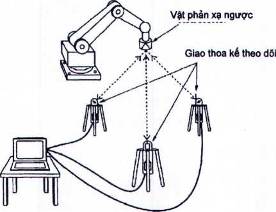
Hình 6 - Phép đo giao thoa bằng nhiều chùm tia laser
4.3.2 Phép đo ba cạnh tam giác bằng siêu âm
Có thể tính toán vị trí của rô bốt trong không gian ba chiều với các dữ liệu về khoảng cách từ ba micro siêu âm tĩnh thu nhận các dòng xung siêu âm từ một nguồn âm thanh được lắp trên rô bốt. Hệ thống thiết bị được giới thiệu trên Hình 7.
Có thể xác định hướng của rô bốt nếu rô bốt có ba nguồn âm thanh độc lập và mỗi micro đặt tĩnh có thể phát hiện các dòng xung từ tất cả ba nguồn âm thanh này.
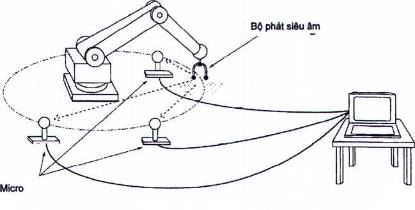
Hình 7 - Đo ba cạnh tam giác bằng siêu âm
4.3.3 Đo ba cạnh tam giác bằng dây cáp
Các phương pháp này dựa trên cơ sở đấu nối ba dây cáp bắt nguồn từ ba cuộn dây cáp cố định cho điểm đầu mút của rô bốt như đã chỉ ra trên Hình 8. Bằng cách đo chiều dài của mỗi dây cáp như khi sử dụng các chiết áp hoặc thước đo mã hóa trên các thiết bị cấp cáp có cơ cấu duy trì sức căng cáp, có thể xác định vị trí của điểm đầu mút trên rô bốt.
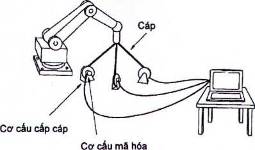
Hình 8 - Đo ba cạnh tam giác bằng cáp cơ khí
4.4 Các phương pháp đo tọa độ cực
Có thể sử dụng các phương pháp đo tọa độ cực để xác định tọa độ Đề các (X, Y, Z) của một điểm trong không gian bằng cách đo khoảng cách D, các giá trị của góc cực (α) và góc nâng (β) như đã chỉ ra trên Hình 9.
4.4.1 Phép đo giao thoa bằng một chùm tia laser
Có thể sử dụng phương pháp đo giao thoa bằng laser để đo vị trí hoặc sự định hướng của rô bốt. Hình 10 giới thiệu một thiết bị điển hình có giao thoa kế một chùm laser để đo vị trí. Có thể tính toán vị trí của rô bốt với các dữ liệu về khoảng cách từ giao thoa kế laser và các dữ liệu về góc cực/ góc nâng thu được từ một hệ thống theo dõi tĩnh nhằm vào một gương phản xạ ngược lắp trên điểm đầu mút của rô bốt.
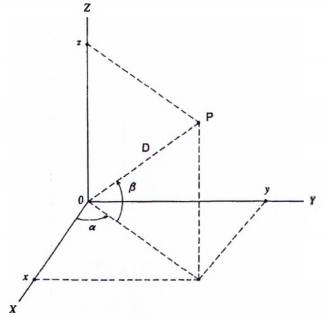
Hình 9 - Nguyên lý của phép đo tọa độ cực theo ba chiều
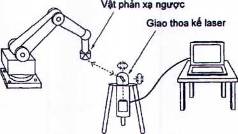
Hình 10 - Phép đo giao thoa bằng một chùm tia laser để đo vị trí
Cũng có thể đo sự định hướng của rô bốt (lắc dọc và quay trệch) khi sử dụng cùng một hệ thống (Hình 11) nếu hệ thống gương phản xạ ngược có khả năng giữ trục quang nhằm vào hệ thống theo dõi tĩnh, hoặc nếu hệ thống theo dõi tĩnh có thể phân tích hình ảnh nhiễu xạ do vật phản xạ ngược phản xạ lại. Phương pháp này có thể thử nghiệm các rô bốt có 6 DOF (bậc tự do)
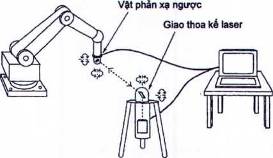
Hình 11 - Phép đo giao thoa bằng một chùm tia laser để đo tư thế
4.4.2 Phương pháp một trạm tổng (cố định /theo dõi)
Có thể đo vị trí đạt được của rô bốt bằng một trạm tổng (cố định/ theo dõi) có khả năng đo khoảng cách, góc góc hướng (cực) và góc tầm (thay cho nâng)) cho từng điểm một.
Tư thế (yếu tố định vị trí) đạt được của rô bốt hoặc quỹ đạo (yếu tố định vị trí) của rô bốt cũng có thể được đo bởi một trạm tổng theo dõi, vị trí này duy trì dấu vết của một vật phản xạ ngược di động lắp trên rô bốt. Hình 12 giới thiệu một thiết bị điển hình cho hệ thống này.
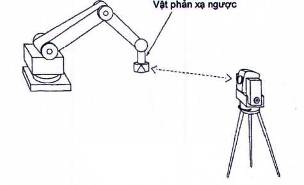
Hình 12 - Phương pháp một trạm tổng (theo dõi)
4.4.3 Phương pháp thước đo thẳng
Có thể đo vị trí của rô bốt như một hàm số của thời gian với các dữ liệu về khoảng cách và các dữ liệu về góc cực / góc nâng từ một thang đo tuyến tính.
Trong phương pháp thước đo thẳng đã chỉ ra trên hình 13, đầu mút phía trên của thước đo thẳng được kết nối với rô bốt và đo khoảng cách giữa đầu mút phía trên và điểm đấu nối tại các cơ cấu mã hóa.
Các dữ liệu về góc cực / góc nâng nhằm vào đầu mút phía trên của thang đo tuyến tính thu được với một cơ cấu mã hóa di chuyển theo hướng nằm ngang và cơ cấu mã hóa thứ hai di chuyển theo phương thẳng đứng.
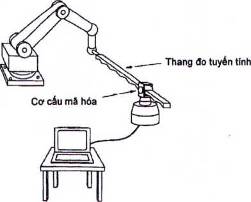
Hình 13 - Phương pháp thang đo tuyến tính
4.5 Các phương pháp tam giác đạc
Phép tam giác đạc là một phương pháp có thể được sử dụng để xác định vị trí của một điểm trong không gian. Trong phép tam giác đạc theo hai chiều, có thể xác định các tọa độ Đề các (x, y) của điểm P (xem hình 14) với chiều dài đường cơ sở B1B2, hai góc cực α1, α2.
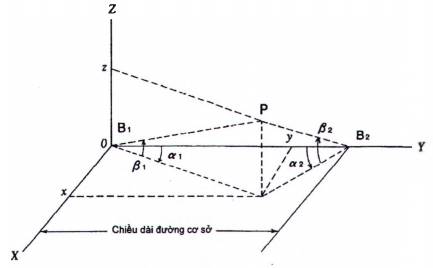
Hình 14 - Nguyên lý đo của phương pháp tam giác đạc
4.5.1 Các phương pháp tam giác đạc theo dõi bằng quang học
Trong các phương pháp này, có thể xác định vị trí của rô bốt như là một hàm số của thời gian với hai bộ các dữ liệu về góc cực / góc nâng từ hai hệ thống theo dõi quang học hai trục. Như vậy, có thể sử dụng các phương pháp này cho cả hai phép đo tĩnh và động. Các hình 15, 16 và 17 giới thiệu các cấu hình điển hình của ba hệ thống tam giác đạc phổ biến theo dõi bằng quang học.
Trong hệ thống theo dõi bằng laser đã chỉ ra trên hình 15, hai chùm tia laser từ hai hệ thống theo dõi liên tục nhằm vào một vật phản xạ lắp trên điểm đầu mút của rô bốt. Phương pháp quét bằng chùm tia laser đã chỉ ra trên hình 16 là một phương pháp khác để xác định vị trí của rô bốt. Phương pháp dựa trên sự phát hiện ánh sáng đi tới một bia lắp trên rô bốt từ ba bộ quét laser phát ra ánh sáng được chiếu thành đường. Hai bộ quét chiếu lên các đường thẳng đứng và bộ quét thứ ba phát ra đường nằm ngang.

Hình 15 - Hệ thống tam giác đạc theo dõi bằng laser
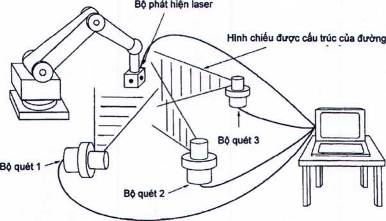
Hình 16 - Hệ thống tam giác đạc quét laser
Có thể tính toán sự định hướng của rô bốt nếu hai chùm tia laser được cấu trúc (có dạng chữ thập) theo dõi một đầu dò dạng khối lập phương được trang bị hai bộ cảm biến dạng vòng CCD trên các bề mặt liền kề của đầu dò.
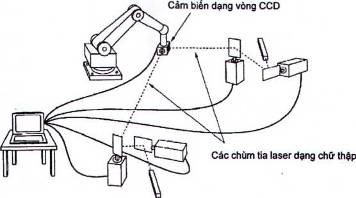
Hình 17 - Hệ thống tam giác đạc theo dõi bằng laser và vòng CCD
4.5.2 Phương pháp máy kinh vĩ (teodolit)
Có thể xác định vị trí đạt được của rô bốt với hai bộ dữ liệu về góc cực / góc nâng bằng cách sử dụng hai (hoặc nhiều hơn hai) máy kinh vĩ (teodolit) tĩnh có các chùm tia nhằm vào một bia lắp trên điểm đầu mút của rô bốt. Thiết bị điển hình được giới thiệu trên hình 18. Có thể tính toán sự định hướng nếu rô bốt có nhiều điểm đích. Các máy kinh vĩ thủ công chỉ được sử dụng có lợi cho các phép đo tĩnh vì chúng được vận hành bằng tay

Hình 18 - Phương pháp máy kinh vĩ (teodolit)
4.5.3 Phương pháp camera quang học
Có thể đo vị trí của rô bốt như một hàm số của thời gian với hình ảnh được chụp bởi hai thiết bị ghi hình (một chiều hoặc hai chiều).
Có thể xác định sự định hướng của rô bốt như một hàm số của thời gian nếu có nhiều nguồn ánh sáng hoặc nhiều bia lắp trên rô bốt để được giám sát bởi các thiết bị ghi hình.
Trong quá trình đo, các nguồn ánh sáng trên rô bốt được bật lên theo thứ tự để có thể biết được nguồn sáng nào đi tới hình ảnh.
Phương pháp này sử dụng hai thiết bị ghi hình (camera) được bố trí ở một khoảng cách cố định đã cho. Hình 19 giới thiệu một thiết bị điển hình dùng cho hệ thống. Các camera giám sát một bia có chiếu sáng được lắp cố định trên điểm đầu mút của rô bốt. Các cơ cấu cảm biến vị trí (hoặc các CCD) được sử dụng để xác định các vị trí của bia trong hệ tọa độ của camera. Thông tin này cùng với hiểu biết về khoảng cách giữa các camera cho phép xác định vị trí của bia.
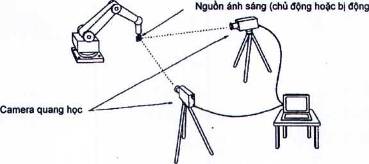
Hình 19 - Phương pháp camera quang học
Có thể đo các đặc tính tư thế và các đặc tính quỹ đạo của rô bốt theo tất cả ba chiều trong không gian bằng ba bộ cảm biến gia tốc tự động (servo) và ba con quay hồi chuyển lắp trên rô bốt mà không có bất cứ thiết bị quan sát ngoại vi nào khi biết trạng thái ban đầu của rô bốt. Hình 20 giới thiệu một thiết bị điển hình dùng cho hệ thống.
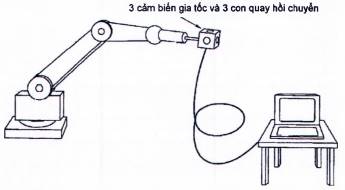
Hình 20 - Phương pháp đo quán tính
4.7 Các phương pháp đo tọa độ (Đề các)
4.7.1 Phương pháp số hóa hai chiều
Có thể đo vị trí hai chiều của rô bốt như các giá trị tọa độ X-Y, Y-Z hoặc Z-X bằng một camera có độ phân giải cao lắp trên rô bốt. Hình 21 giới thiệu một thiết bị điển hình cho hệ thống. Camera đếm các vạch của thang đo có độ chính xác cao trên tấm tạo thành các vạch của mặt phẳng thử.
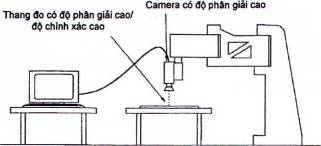
Hình 21 - Phương pháp số hóa hai chiều 1
Có thể đo vị trí hai chiều của rô bốt trong vùng bị giới hạn theo nguyên lý đo giao thoa có độ phân giải dưới micrômet. Biểu đồ Moire tạo ra trên tấm mạng lưới đã được đầu quét bắt lấy và được phân tích để cho các giá trị gia tăng theo hai chiều (hình 22).
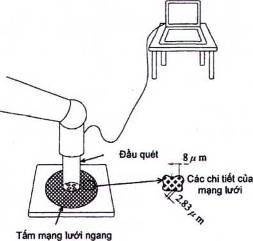
Hình 22 - Phương pháp số hóa hai chiều 2
Có thể đo vị trí của rô bốt như các giá trị tọa độ X-Y, Y-Z hoặc Z-X với một bút số hóa lắp trên rô bốt và một bộ các bảng nhỏ dùng làm mặt phẳng thử (hình 23). Phương pháp này có thể được sử dụng để hiệu chuẩn cho từng điểm hoặc các chuyển động theo quỹ đạo liên tục. Như vậy, có thể dùng phương pháp này cho cả các phép đo tĩnh và động.
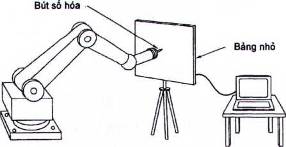
Hình 23 - Phương pháp số hóa hai chiều 3
4.7.2 Phương pháp máy đo tọa độ
Có thể đo vị trí đạt tới của rô bốt bằng cách nhận được các giá trị tọa độ của điểm đích rô bốt với một máy đo tọa độ (hình 24). Cũng có thể đo sự định hướng đạt tới của rô bốt bằng cách thu nhận các giá trị tọa độ của ba hoặc nhiều hơn ba điểm thông qua tiếp xúc với một bia dạng khối lập phương.
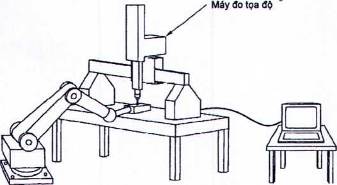
Hình 24 - Phương pháp máy đo tọa độ
Có thể ghi lại trên giấy quỹ đạo theo hai chiều của rô bốt với các bút phun mực cơ khí, điện hoặc điện tử. Hình 25 giới thiệu một ví dụ sử dụng giấy phóng điện trong ghi fax. Có thể đo các đặc tính vận tốc của rô bốt nếu phát ra các xung đồng bộ hóa.
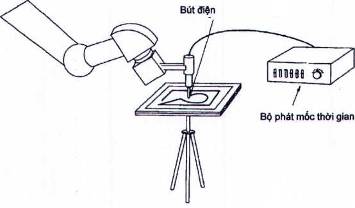
Hình 25 - Phương pháp vẽ quỹ đạo
Bảng 1 - Phương pháp đo các đặc tính đặc trưng của rô bốt
Bảng 2 - Các đặc tính điển hình về đo của các phương pháp đo trong bảng 1
| Các phương pháp đo | Đặc tính của dụng cụ đo | Đặc tính đo | Vận tốc lớn nhất của quỹ đạo | Tốc độ lấy mẫu cho đo quỹ đạo | |||
| Độ phân giải | Khả năng lặp lại | Độ chính xác | CH tĩnh | - | - | ||
| 4.1 Các phương pháp định vị đầu dò thử | 0.01 -1 µm 0.05% trường nhìn | 0-001 -0.01mm 0.1 - 1 % trường nhìn | 0.002 - 0.02mm | ||||
| 4.2.1 So sánh theo thước mẫu cơ khí | 0.025-0.1 mm | 0.05 - 0.2 mm | Động |
|
| ||
| 4.2-2 So sánh quỹ đạo nhờ chùm tia laser | 3μm | 0.02 mm | Động | 10 m/s | 0.01 ms/điểm | ||
| 4.3.1 Đo giao thoa theo dõi bằng nhiều chùm tia laser | 0.16 μm | 2 μm | 0.005 - 0.01 mm | Động | 6 m/s | 10-100 ms/điểm | |
| 4.3.2 Đo ba cạnh tam giác bằng siêu âm | 0.05-1mm | 0.2 - 1mm | 0.4 - 3 mm |
| 100-1000 ms/điểm | ||
| 4.3.3 Đo ba cạnh tam giác bằng cáp cơ khí | 0.01 mm | 0.02 mm | 0.3 mm | 5 m/s | 0.5 ms/điểm | ||
| 4.4.1 Đo giao thoa theo dõi bằng một chùm tia laser | 0.6 - 5 μm | 0.005 - 0.02 mm | 0.005 - 0-05 mm | Động | 6 m/s | 0.01-500 ms/điểm | |
| 4.4.2 Phương pháp một vị trí tổng - theo dõi | 0.2 mm 5 cung - giây | 3mm 10 cung -giây | 1 m/s | 500-3000 ms/điểm | |||
| 4.4.3 Phương pháp thang đo tuyến tính | 0.02 mm | 0.1 mm | 0.5 - 1 mm |
|
| ||
| 4.5.1 Phép tam giác đạc theo dõi bằng quang học | 2 cung - giây 0.015% | 5 cung - giây | 10 cung - giây | Động | 2-10 m/s | 1 ms/điểm | |
| 4.5.2 Phương pháp máy kinh vĩ | 0.1 - 0-2 cung-giây | 0.5 - 2 cung-giây | 0.5 - 2 cung-giây, 1mm | Chỉ tĩnh | - | - | |
| 4.5.3 Phương pháp camera quang học | 0.0005 - 0.025% | 0.001-0.05% | 0.01 - 0-75% | Động | 10 m/s | 0.2-4 ms/điểm | |
| 4.6 Phương pháp đo quán tính | 5 μm | 0.01 mm | 0.03 mm | Động | 5 m/s | 3 ms/điểm | |
| 4.7.1 Phương pháp số hóa hai chiều | 0.01 - 0.02mm | 0.02 - 0.2 mm | 0.1 - 0.5 mm | Động | 0.5 - 3 m/s | 10-100 ms/điểm | |
| 4.7.2 Phương pháp (sàn) máy đo tọa độ | 0.5 μm | 0.5 μm | 0.01 mm | Chỉ tĩnh | - | - | |
| 4.8 Phương pháp vẽ quỹ đạo | 0.2 mm | 0.2 - 0.5 mm | Động |
|
| ||
| CHÚ THÍCH 1: | Các dữ liệu được giới thiệu trong bảng này dựa trên các đặc tính kỹ thuật danh nghĩa của nhà sản xuất. Nên tham vấn các nhà sản xuất về kiểm tra các yêu cầu đặc tính hoặc mô tả các giới hạn. | ||||||
| CHÚ THÍCH 2: | Phần lớn tính lặp lại hoặc các giá trị độ chính xác trong bảng này là các đặc tính lý thuyết khi thiết bị đo riêng được lắp đặt cẩn thận và khi độ ổn định kích thước của toàn hệ thống đo được duy trì trong quá trình đo. | ||||||
Phụ lục A. Ví dụ về các hệ thống đo / cảm biến sẵn có
Một số ví dụ về các bộ cảm biến thích hợp cho phép đo vị trí cũng đã được liệt kê trong phụ lục này
| Các phương pháp đo | Các hệ thống/ cảm biến sẵn có (nhà sản xuất/ quốc gia) |
| 4.1 Phương pháp định vị đầu dò thử | REFCUBE 6D (KRYPTON. Belgium) RPMS 200 (Sun Japan, Japan) |
| 4.2.1 Phương pháp so sánh theo thước mẫu cơ khí |
|
| 4.2.2 Phương pháp so sánh quỹ đạo nhờ chùm tia laser | ROBOTEST (Polytec, Germany) |
| 4.3.1 Phép đo giao thoa theo dõi bằng nhiều chùm tia laser | CMS-3000 cấu hình đo ba cạnh tam giác (Chesapeake Laser System, USA) LTS-1000 (LK Tool, USA) LTCMS (Tokyo, Seimitsu, Japan) |
| 4.3.2 Phép đo ba cạnh tam giác bằng siêu âm |
|
| 4.3.3 Phép đo ba cạnh tam giác bằng cáp cơ khí | CompuGauge (Dynalog, USA) RoboTrak (Robot Simulations, UK) |
| 4.4.1 Phép đo giao thoa theo dõi bằng một chùm tia laser | ROBOTEST (Polytec, Germany) SMART310 (Leica, Switzerland) CMS-3000 (Chesapeake Laser System, USA) |
| 4.4.2 Phương pháp một vị trí tổng (tĩnh / theo dõi) | Static: PCM1 (Leica, Switzerland) MONMOS (Sokkia, Japan) Tracking: AP-L1 (Topcon, Japan) |
| 4.4.3 Phương pháp thang đo tuyến tính |
|
| 4.5.1 Phép tam giác đạc theo dõi bằng quang học | OPTOTRAC (MSSR Group, University of Surrey, UK) LASERTRACE (Automatic System Laboratories, UK) LASER TRACKER LTS8000 (KRYPTON, Belgium) |
| 4.5.2 Phương pháp máy kinh vĩ | ECDS (Leica, Switzerland) |
| 4.5.3 Phương pháp camera quang học | MultiLab System (SELCOM AB, Sweden) RPM 9200 (Qualisys, Sweden) RODYM 6D (KRYPTON, Belgium) OPT-FOLLOW (YA-MAN Hamilton, USA) Optotrak (Northern Digital, Canada) ICAROS (Imar GmbH, Germany) Hl-Speed Tracker X 2 (EMTEC, Japan) Two-dimensional PSD S1300 (Hamamatsu Photonics, Japan) |
| 4.6 Phương pháp đo quán tính | ICAROS (Imar GmbH, Germany) |
| 4.7.1 Phương pháp số hóa hai chiều | RODYM 2.5D (KRYPTON, Belgium) PP109R (Heidenhain, Germany) MODEL 200 (Zimmer, Germany) DrawingPad (CalComp, USA) |
| 4.7.2 Phương pháp máy đo tọa độ | Desk top CMM: GEOTIZER 500 (Mitutoyo, Japan) Portable CMM: SYSTEM 6 (ROMER, USA) |
| 4.8 Phương pháp vẽ quỹ đạo |
|
Phụ lục B. Địa chỉ các nhà sản xuất hệ thống đo / cảm biến
| Nhà sản xuất hệ thống đo / cảm biến | Địa chỉ |
| ADE Corp. (USA) | 77 Rowe Street, Newton, Massachusetts, 02166 USA |
| Automatic Systems Laboratories (UK) | 28 Blundells Road, Bradville, Milton keynes England |
| Calcomp (USA) | 14555 North 82nd street, Scottsdale, Arizona, USA |
| Chesapeake Laser System, Inc, USA | 222 Gale Lane, Kennett Square, Pennsylvania, USA |
| Dynalog, Inc, USA | 2727 Second Avenue, Detroit, Michigan, 48201 USA |
| EMTEC, (Japan) | 1510-1, Kaitori, Tama-City, Tokyo, 206 Japan |
| Hamamatsu Photonics K.K Japan | 1126-1 Ichino-cho, Hamamatsu City, Shizuoka, Japan |
| DR. JOHANNES HEIDENHAIN Germany | Dr-Johannes-Heidenhain-Strasse 5, Germany |
| iMAR GmbH Germany | LPA @ University of Saariland Germany |
| KRYPTON Electric Eng (Bengium) | Interleuvenlaan 86, B-3001 Leuven, Bengium |
| LK Tool Inc (USA) | 1625 W. University Drive, temp, Arizona, USA |
| Leica AG (Switzerland) | CH-5035 Unterentfelden, Switzerland |
| Mitutoyo (japan) | 31-19, Shiba 5-chome, Tokyo, Japan |
| Northern Digital Inc (Canada) | 403 Alber street, Waterloo, Ontario, Canada |
| Polytec GmbH (Germany) | Postfach 161, D-76333 Waldbronn, Karlsruhe, Germany |
| Qualisys AB (Sweden) | S-433 30 Partille, Sweden |
| ROMER (USA) | 806 Oakwood Boulevard Michigan USA |
| Robot Simulations Ltd. (UK) | Lynnwood Business Center, newcastle, UK |
| SELCOM AB (Sweden) | Box 250, S-433 25 Partite Sweden |
| Sokkia Co. Ltd (Japan) | 1-1 Tomigaya Shibuya-ku, Tokyo, Japan |
| Sun Japan Corp. (Japan) | Kyokuko Chuo-ku, Tokyo, 151 Japan |
| University of Surrey, MSSR Group (UK) | Guildford, Surrey G02 5XH, England |
| Tokyo Seimitsu Co. Ltd (Japan) | 7-1, Shimo-Renjaku 9-chome, Mitaka, Tokyo, Japan |
| YA-MAN LTD, Hamilton Lab (USA) | 2005 Hamilton Avenue Suit 100, San Jose, USA |
| ZIMMER GmbH (Germany) | Industriestrasse 1, D-64380 Rossdorf/Darmstadt GM |
Phụ lục C. Thư mục tài liệu tham khảo
1. TCVN 13696 (ISO 9283), Tay máy rô bốt công nghiệp - Đặc tính và các phương pháp thử có liên quan.
2. ANSI/RIA R15.05 - 1- 1990 “American National Standard for Industrial Robots and Robot Systems - Ponit-to-Point and static Performance Characteristics - Evaluation”.
3. ANSI/RIA R15.05 - 2 “American National standard for Industrial Robots and Robot Systems - Path - related and Dynamic Performance Characteristics - Evaluation”.
4. VDI (Germany Industrial standard) 2861, Blatt 2, 1987.
5. Lau, K., Hocken, R.J., “A Survey of Current Robot metrology Methods,” Annals of the CIRP, Vol. 32, No 2, pp. 485-488, 1984.
6. Jiang, B.C., Black, J.T., Duraisamy, R., (Auburn University), “A Review of recent Development in Robot Metrology,” J. of Manufacturing Sysstems, Vol. 7 No. 4, (1988) pp. 339 - 357.
7. Lombard, J., Perrot, J.C., 1983, “Automatic Measurement of the Positioning Accuracy of Industrial Robots, “ Annals of the CIRP, Vol. 32/1, pp. 297-299.
8. Lau, K., Hocken, R., 1986, “An Overview of Techniques for Robot Performance Measurements,” Internal Report, NIST.
9. Freeman, S., 1987, “New perspectives in 3D Theodolite - base Industrial Measuring Systems,” Quality Today, May 1987, pp. 74-77.
10. MacFarelane, J., Donath, M., 1984, “Tracking Robot Motion in Three Dimensional Space: a Laser Scanning Approach,” NATO ASI series, F11, pp. 309-318.
11. Lau, K., Hocken, R., Haight, w„ “Automatic Laser Tracking Interferometer System for Robot Metrology,” Precision Engineering, Vol. 8 No. 1, pp. 3-8, January 1986.
12. Lau, K., Hocken, R., Haynes, L., (NBS) 1985, “Robot Performance Measurements using Automatic Laser Tracking Techniques,” Robotics and Computer Integrated Manufacturing, Vol. 2 No.3, pp. 227-236.
13. Gilby, J.H., Parker, G.A., “Laser Tracking System to Measure Robot Arm Performance.” Sensor Review, pp. 180-184, October 1982.
14. Prenninger, J.P., 1992 “Position and Orientation measurement of Industrial Robots using Laser Tracking Techniques in Six Degrees of Freedom,” Doctor Thesis, Institute of Flexible Automation, TU Vienna.
15. Becker, P.J., Bolle, H., Mitschke, H., 1984, “Lasertriangulation fur die genaue dreidimensionale Vermessung von Robotem,“ FHG berichte Vol.2, pp. 47-50.
16. Prenniger, J.P., Vincze, M., Gander, H., 1983, “Contactless Position and Orientation Measurement of Robot End-Effector," Proc. Of IEEE Conference on robotics and Automation, pp. 183-189.
17. Gilby, J., ea al., 1984, “Dynamic Performance Measurement of Robot Arms,” Department of Mechanical Engineering, University of Surrey, Guilford, Surrey, England.
18. Val Brussel, H., 1990, “Evaluation and Testing of Robots,” Annals of CIRP Vol. 39/2, pp. 657- 664.
19. McEntire, R, H., 1976, “Three Dimensional Accuracy Measuremet Method for Robots,” The Industrial Robot, Vol 3, pp. 105-112.
20. Vincze, M., Prenniger, J.P., Gander, H., "A Six Degree of Freedom Robot Measurment System III: Application of Measurment Data to System Calibration," Int. Symp. On Theory of Machines and Mechanisms, Nagoya, Japan, Sept. 24-26, 1992.
21. Van den Bossche, J., Van Brussel, H., 1989, “RODYM: a New Approach to Robot Metrology,” Internal Report, the Catholic University of Leuven, Belgium.
22. “Internatioanl Encyclopendia of Robotics - Volume 3: Applications and Automaton” John Wiley & Sons.
23. Hinuber, E. V., Janocha, H., “Intertial Measurment System for Industrial Robots”.
24. Day, C.P. “Robot Accuracy Issues methods of Improvement” Robotics Today (SME), Volume 1, Number 1, Spring 1988.
25. Nakamura, O., Goto, M., Toyoda, K., Tanimura, N., Kurosawa, T., (National research Laboratory of Metrology et al) “Development of a Coordinate Measuring System with Tracking Laser Interferometers” Annals of CIRP, Vol. 40, No. 1 (August, 1991) pp. 523-526.
26. Nakamura, O., Goto, M., Toyoda, K., takai, N., Kurosawa, T., (National research Laboratory of Metrology et al) “Developmet of a Coodinate Measuring system with tracking laser interferometers”
27. Prenninger, J.P., gander, H., Vincze, M., “Real time 6-DOF Measurment of Robot End Effector” Proceedings of International Robot and Vision Automation Conference.
28. Seto, T., “Method for Measurment of Large Scale Dimension using Field Surveying Intrustment” In Japanese
29. Aoyagi, S., Kamiya, y., Okabe, S., “Development of Automatic Tracking System of 3-D Position of a Robot”
30. Oiwa, T., Suzuki, M., Kyusojin, A., “Spatial Coordinate Measurment using Structured Laser Light and a Spherical Mirror”
31. Brown, L.B., “Interferometric Accuracy in Three - Dimensional Measurment: A precision Laser Tracking System”
32. Gottwald, R., “SPACE - An Automated Non - contact 3-D - Measuring - System for Industrial Applications”
33. Priel, m., (LNE, Trance) “Evaluating the Performance of Industrial Robots”
34. Mayer, J.R.R., parker, A., “A Portable Intrusment for 3 - D Dynamic Robot Measurments Using Triangulation and laser Tracking”

