Statistical quality control - Acceptance inspection by attributes with acceptance number zero
Lời nói đầu
TCVN 4442 : 2009 thay thế cho TCVN 4442-1987;
TCVN 4442 : 2009 do Ban kỹ thuật tiêu chuẩn quốc gia TCVN/TC 69 Ứng dụng các phương pháp thống kê biên soạn, Tổng cục Tiêu chuẩn Đo lường Chất lượng đề nghị, Bộ Khoa học và Công nghệ công bố.
KIỂM SOÁT CHẤT LƯỢNG BẰNG PHƯƠNG PHÁP THỐNG KÊ - KIỂM TRA NGHIỆM THU ĐỊNH TÍNH VỚI SỐ CHẤP NHẬN BẰNG KHÔNG
Statistical quality control - Acceptance inspection by atributes with acceptance number zero
Tiêu chuẩn này quy định các phương án kiểm tra định tính không cho phép có sản phẩm có khuyết tật trong mẫu. Các phương án kiểm tra này được áp dụng khi cần giảm chi phí kiểm tra.
Tài liệu viện dẫn dưới đây rất cần thiết cho việc áp dụng tiêu chuẩn này. Đối với các tài liệu ghi năm công bố thì áp dụng bản được nêu. Đối với các tài liệu không ghi năm công bố thì áp dụng bản mới nhất, bao gồm cả các sửa đổi.
TCVN 3691, Thống kê học - Thuật ngữ và ký hiệu
TCVN 4441 : 2009, Phương pháp lấy mẫu ngẫu nhiên sản phẩm dạng đơn chiếc
Tiêu chuẩn này áp dụng các thuật ngữ và định nghĩa trong TCVN 3691.
4.1. Để lập phương án kiểm tra cần xác định:
a) danh mục các thông số cần kiểm tra;
b) cỡ lô N;
c) số sản phẩm có khuyết tật giới hạn G trong lô;
d) rủi ro của người nhận b, trong tiêu chuẩn quy định b = 10 và 5 %
b là xác suất nhận lô có số sản phẩm có khuyết tật bằng G. Thay cho G có thể sử dụng mức chất lượng giới hạn LQ. Giữa LQ và G có hệ thức:
![]() (1)
(1)
Giá trị của G được làm tròn tới số nguyên nhỏ hơn gần nhất.
4.2. Phương pháp lấy mẫu được tiến hành theo các quy định trong TCVN 4441:2009.
4.3. Khi kiểm tra các sản phẩm trong mẫu, nếu có một thông số có giá trị không thỏa mãn yêu cầu thì ngừng kiểm tra và lô bị loại.
Các ví dụ minh họa trình bày trong Phụ lục A.
5.1. Cỡ mẫu được xác định theo công thức:
n = N x f (G) (2)
Kết quả được làm tròn tới số nguyên gần nhất.
Hệ số f(G) cho trong Bảng 1 với b = 10 % và Bảng 2 với b = 5 %.
5.2. Khi G > 50, f(G) xác định theo công thức:
![]() b = 10 % (3)
b = 10 % (3)
hoặc
![]() b = 5 % (4)
b = 5 % (4)
Bảng 1 - Giá trị hệ số f(G) với b = 10 %
| G | f(G) | G | f(G) | G | f(G) | G | f(G) | G | f(G) |
| 0 | — | 10 | 0,206 | 20 | 0,100 | 30 | 0,074 | 40 | 0,056 |
| 1 | 0,900 | 11 | 0,189 | 21 | 0,104 | 31 | 0,072 | 41 | 0,055 |
| 2 | 0,684 | 12 | 0,175 | 22 | 0,100 | 32 | 0,070 | 42 | 0,054 |
| 3 | 0,536 | 13 | 0,163 | 23 | 0,096 | 33 | 0,068 | 43 | 0,053 |
| 4 | 0,438 | 14 | 0,152 | 24 | 0,092 | 34 | 0,066 | 44 | 0,051 |
| 5 | 0,370 | 15 | 0,143 | 25 | 0,088 | 35 | 0,064 | 45 | 0,050 |
| 6 | 0,319 | 16 | 0,135 | 26 | 0,085 | 36 | 0,062 | 46 | 0,049 |
| 7 | 0,281 | 17 | 0,127 | 27 | 0,082 | 37 | 0,061 | 47 | 0,048 |
| 8 | 0,251 | 18 | 0,121 | 28 | 0,079 | 38 | 0,059 | 48 | 0,047 |
| 9 | 0,226 | 19 | 0,115 | 29 | 0,077 | 39 | 0,058 | 49 | 0,046 |
Bảng 2 - Giá trị hệ số f(G) với b = 5 %
| G | f(G) | G | f(G) | G | f(G) | G | f(G) | G | f(G) |
| 0 | — | 10 | 0,259 | 20 | 0,140 | 30 | 0,096 | 40 | 0,073 |
| 1 | 0,950 | 11 | 0,239 | 21 | 0,133 | 31 | 0,093 | 41 | 0,071 |
| 2 | 0,777 | 12 | 0,239 | 22 | 0,128 | 32 | 0,090 | 42 | 0,069 |
| 3 | 0,632 | 13 | 0,206 | 23 | 0,123 | 33 | 0,087 | 43 | 0,068 |
| 4 | 0,528 | 14 | 0,193 | 24 | 0,118 | 34 | 0,085 | 44 | 0,066 |
| 5 | 0,451 | 15 | 0,182 | 25 | 0,113 | 35 | 0,083 | 45 | 0,065 |
| 6 | 0,394 | 16 | 0,171 | 26 | 0,109 | 36 | 0,080 | 46 | 0,064 |
| 7 | 0,349 | 17 | 0,162 | 27 | 0,106 | 37 | 0,078 | 47 | 0,062 |
| 8 | 0,313 | 18 | 0,154 | 28 | 0,102 | 38 | 0,076 | 48 | 0,061 |
| 9 | 0,284 | 19 | 0,146 | 29 | 0,099 | 39 | 0,074 | 49 | 0,060 |
Để đánh giá hiệu quả của phương án kiểm tra đã chọn, cần xác định gần đúng một số điểm (p, Pa) của đường hiệu quả bằng cách tính mức chất lượng p tương ứng với xác suất chấp nhận Pa cho trước theo công thức:
![]() (5)
(5)
trong đó giá trị hệ số m phụ thuộc vào Pa cho trong Bảng 3,
Bảng 3
| Pa | m | |
| b = 10 % | b = 5 % | |
| 0,99 | 0,44 | 0,34 |
| 0,95 | 2,23 | 1,71 |
| 0,90 | 4,58 | 3,52 |
| 0,75 | 12,5 | 9,60 |
| 0,50 | 30,1 | 23,1 |
| 0,368 | 43,4 | 33,4 |
| 0,25 | 60,2 | 46,3 |
| 0,10 | 100 | 76,9 |
| 0,05 | 130 | 100 |
| 0,01 | 200 | 154 |
7. Mức chất lượng trung bình sau kiểm tra (AOQ)
7.1. Mức chất lượng trung bình sau kiểm tra là mức chất lượng của các sản phẩm được nhận theo phương án kiểm tra đã chọn, trong đó những lô bị loại đã được kiểm tra 100 % và thay sản phẩm có khuyết tật bằng sản phẩm đạt yêu cầu.
7.2. Mức chất lượng trung bình sau kiểm tra được tính theo công thức:
AOQ = p x Pa 6)
Trường hợp không thể thay thế sản phẩm có khuyết tật bằng sản phẩm đạt yêu cầu thì mức chất lượng trung bình sau kiểm tra, ký hiệu là AOQ’, được tính theo công thức:
AOQ’ = ![]() (7)
(7)
7.3. Giới hạn mức chất lượng trung bình sau kiểm tra AOQL có thể tính gần đúng theo (6) hay (7) với Pa = 0,368.
8. Đánh giá mức chất lượng trung bình trước và sau kiểm tra
8.1. Để đánh giá mức chất lượng trung bình trước và sau kiểm tra cần kiểm tra một loạt các lô (ít nhất là 10) được xem là có cùng mức chất lượng và do cùng một nơi sản xuất. Những lô bị loại phải được kiểm tra 100 %.
Sau khi kiểm tra l lô, xác định các đại lượng sau:
a) cỡ lô Ni (1 £ i £ l);
b) số sản phẩm có khuyết tật Mi được phát hiện trong lô thứ i, nếu lô này được nhận thì Mi = 0;
c) cỡ mẫu ni của lô thứ i được kiểm tra.
8.2. Mức chất lượng trung bình sau kiểm tra được đánh giá theo công thức:
![]() (8)
(8)
trong đó:
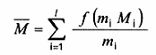 (9)
(9)
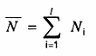 (10)
(10)
 (11)
(11)
Hệ số f(miMi) xác định theo bảng 4. Trong công thức (9), chỉ lấy tổng theo những lô bị loại khi kiểm tra mẫu.
8.3. Nếu không thể thay thế sản phẩm có khuyết tật bằng sản phẩm đạt yêu cầu thì đánh giá AOQ’ theo công thức:
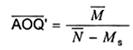 (12)
(12)
trong đó:
![]() (13)
(13)
8.4. Mức chất lượng trung bình trước kiểm tra ![]() không phụ thuộc vào việc thay thế sản phẩm có khuyết tật và được xác định theo công thức:
không phụ thuộc vào việc thay thế sản phẩm có khuyết tật và được xác định theo công thức:
![]() (14)
(14)
Bảng 4 - Giá trị hệ số f(miMi)
| miMi | f(miMi) | miMi | f(miMi) | miMi | f(miMi) | miMi | f(miMi) |
| 0,0 | 1,00 | 2,0 | 0,31 | 4,0 | 0,07 | 6,0 | 0,02 |
| 0,1 | 0,95 | 2,1 | 0,29 | 4,1 | 0,07 | 6,1 | 0,01 |
| 0,2 | 0,90 | 2,2 | 0,27 | 4,2 | 0,06 | 6,2 | 0,01 |
| 0,3 | 0,86 | 2,3 | 0,26 | 4,3 | 0,06 | 6,3 | 0,01 |
| 0,4 | 0,81 | 2,4 | 0,24 | 4,4 | 0,05 | 6,4 | 0,01 |
| 0,5 | 0,77 | 2,5 | 0,22 | 4,5 | 0,05 | 6,5 | 0,01 |
| 0,6 | 0,73 | 2,6 | 0,21 | 4,6 | 0,05 | 6,6 | 0,01 |
| 0,7 | 0,69 | 2,7 | 0,19 | 4,7 | 0,04 | 6,7 | 0,01 |
| 0,8 | 0,65 | 2,8 | 0,18 | 4,8 | 0,04 | 6,8 | 0,01 |
| 0,9 | 0,62 | 2,9 | 0,17 | 4,9 | 0,04 | 6,9 | 0,01 |
| 1,0 | 0,58 | 3,0 | 0,16 | 5,0 | 0,03 | 7,0 | 0,01 |
| 1,1 | 0,55 | 3,1 | 0,15 | 5,1 | 0,03 | 7,1 | 0,01 |
| 1,2 | 0,52 | 3,2 | 0,14 | 5,2 | 0,03 | 7,2 | 0,01 |
| 1,3 | 0,49 | 3,3 | 0,13 | 5,3 | 0,03 | 7,3 | 0,00 |
| 1,4 | 0,46 | 3,4 | 0,12 | 5,4 | 0,02 | 7,4 | 0,00 |
| 1,5 | 0,43 | 3,5 | 0,11 | 5,5 | 0,02 | 7,5 | 0,00 |
| 1,6 | 0,40 | 3,6 | 0,10 | 5,6 | 0,02 | 7,6 | 0,00 |
| 1,7 | 0,38 | 3,7 | 0,09 | 5,7 | 0,02 | 7,7 | 0,00 |
| 1,8 | 0,36 | 3,8 | 0,09 | 5,8 | 0,02 | 7,8 | 0,00 |
| 1,9 | 0,33 | 3,9 | 0,08 | 5,9 | 0,02 | 7,9 | 0,00 |
VÍ DỤ 1:
Số sản phẩm có khuyết tật giới hạn cho lô có cỡ N = 250 là G = 5. Rủi ro người nhận 10 %. Tìm phương án kiểm tra có số chấp nhận bằng không (0) tương ứng và một số điểm của đường hiệu quả, mức chất lượng trung bình sau kiểm tra.
Theo Bảng 1, với G = 5, được f(G) = 0,370. Theo công thức (2) ta được:
n = N x f(G) = 250 x 0,370 = 92,5 » 92
Theo (5), với Pa” = 0,90 được:
![]()
Một số điểm khác của đường hiệu quả cho trong Bảng A.1.
Bảng A.1
| Pa” | m | P, % |
| 0,99 | 0,44 | 0,0088 |
| 0,95 | 2,23 | 0,045 |
| 0,90 | 4,58 | 0,092 |
| 0,75 | 12,5 | 0,25 |
| 0,50 | 30,1 | 0,602 |
| 0,368 | 43,4 | 0,868 |
| 0,25 | 60,2 | 1,204 |
| 0,10 | 100 | 2,0 |
| 0,05 | 130 | 2,6 |
| 0,01 | 200 | 4,0 |
Mức chất lượng trung bình sau kiểm tra xác định theo (6) và (7) cho trong Bảng A.2.
Bảng A.2
| Pa” | P, % | AOQL, % | AOQ, % |
| 0,99 | 0,0088 | 0,0087 | 0,0087 |
| 0,95 | 0,045 | 0,0427 | 0,0427 |
| 0,90 | 0,092 | 0,0828 | 0,0828 |
| 0,75 | 0,25 | 0,1875 | 0,1876 |
| 0,50 | 0,602 | 0,301 | 0,3019 |
| 0,368 | 0,868 | 0,319 | 0,3212 |
| 0,25 | 1,204 | 0,301 | 0,3037 |
| 0,10 | 2,0 | 0,20 | 0,2036 |
| 0,05 | 2,6 | 0,13 | 0,1333 |
| 0,01 | 4,0 | 0,04 | 0,0416 |
Giới hạn mức chất lượng trung bình sau kiểm tra AOQL là giá trị của AOQ ứng với Pa = 0,368 là AOQL = 0,319 %.
VÍ DỤ 2:
10 lô liên tiếp có cỡ N = 250 được kiểm tra. Cỡ mẫu n = 92. Các lô bị loại được kiểm tra 100 %, các sản phẩm có khuyết tật được thay bằng sản phẩm tốt. Kết quả như sau:
Xác định mức chất lượng trung bình trước và sau kiểm tra. Theo (11):
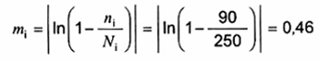
Theo (10):
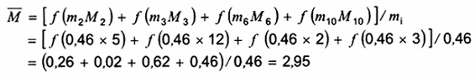
| Thứ tự lô | Quyết định | Mi |
| 1 | Nhận | 0 |
| 2 | Loại | 5 |
| 3 | Loại | 12 |
| 4 | Nhận | 0 |
| 5 | Nhận | 0 |
| 6 | Loại | 2 |
| 7 | Nhận | 0 |
| 8 | Nhận | 0 |
| 9 | Nhận | 0 |
| 10 | Loại | 3 |
Theo (9):
![]() = 10 x N = 2 500
= 10 x N = 2 500
Theo (8):
![]()
Để xác định mức chất lượng trung bình trước kiểm tra ![]() trước hết phải tính giá trị Ms. Theo (13):
trước hết phải tính giá trị Ms. Theo (13):
Ms = M2 + M3 + M6 + M10 = 5 + 12 + 2 + 3 = 22
Theo (12):
![]()
MỤC LỤC
5. Xác định cỡ mẫu
6. Xác định đường hiệu quả
7. Mức chất lượng trung bình sau kiểm tra (AOQ)
8. Đánh giá mức chất lượng trung bình trước và sau kiểm tra
Phụ lục A (tham khảo) Các ví dụ

