ĐỘ TIN CẬY TRONG KỸ THUẬT – PHƯƠNG ÁN LẤY MẪU MỘT LẦN KIỂM TRA THỜI GIAN LÀM VIỆC KHÔNG HỎNG CÓ PHÂN BỐ WEIBULL
Reliability in technique – Single stage alternative testing plans with Weibull no failure operation time distribution
Lời nói đầu
TCVN 4555 : 2009 thay thế cho TCVN 4555-1988;
TCVN 4555 : 2009 do Ban kỹ thuật tiêu chuẩn quốc gia TCVN/TC 69 Ứng dụng các phương pháp thống kê biên soạn, Tổng cục Tiêu chuẩn đo lường Chất lượng đề nghị, Bộ Khoa học và Công nghệ công bố.
ĐỘ TIN CẬY TRONG KỸ THUẬT – PHƯƠNG ÁN LẤY MẪU MỘT LẦN KIỂM TRA THỜI GIAN LÀM VIỆC KHÔNG HỎNG CÓ PHÂN BỐ WEIBULL
Reliability in technique – Single stage alternative testing plans with Weibull no failure operation time distribution
Tiêu chuẩn này áp dụng cho việc kiểm tra mẫu các sản phẩm kỹ thuật sản xuất hàng loạt theo phương án kiểm tra qua thử nghiệm một lần, không thay thế sản phẩm hỏng. Tiêu chuẩn này được sử dụng khi thời gian làm việc không hỏng của sản phẩm tuân theo luật phân bố Weibull.
2. Thuật ngữ, định nghĩa và ký hiệu
2.1. Thuật ngữ và định nghĩa
Tiêu chuẩn này sử dụng các thuật ngữ và định nghĩa trong TCVN 8244 (ISO 3534), Thống kê học – Từ vựng và ký hiệu.
2.2. Ký hiệu
p : Tỷ lệ sản phẩm hỏng trong lô
AQL : Mức chất lượng chấp nhận
a, b : Mức rủi ro của người giao và người nhận
AQL* : Trị số giả định về mức chất lượng chấp nhận dùng để xác định phương án kiểm tra trong trường hợp t1 < t0
LQ : Mức chất lượng không chấp nhận là mức chất lượng nhỏ nhất không chấp nhận trong lô kiểm tra nghiệm thu. Với phương án đã cho xác suất không chấp nhận lô sản phẩm không đạt là cao và bằng 1 – b
t0 : Thời gian làm việc không hỏng trung bình cho trước
t1 : Thời gian thử nghiệm cho trước
N : Số sản phẩm của lô cần kiểm tra
n : Số sản phẩm rút ra từ lô để kiểm tra (sản phẩm mẫu)
Ac : Số chấp nhận của phương án kiểm tra
r : Số sản phẩm hỏng của mẫu trong thời gian thử nghiệm t1
l1(t0) : Cường độ hỏng trong trường hợp P = AQL
l2(t0) : Cường độ hỏng trong trường hợp P = LQ
3.1. Để có thể sử dụng tiêu chuẩn này thì phân bố thống kê thời gian làm việc không hỏng của sản phẩm phải có dạng hàm Weibull với các tham số đã biết.
Việc khảo sát sự phù hợp của các số liệu thực nghiệm với phân bố lý thuyết dạng hàm Weibull và xác định các tham số của nó phải theo các phương pháp chung và được thỏa thuận giữa nhà sản xuất và người tiêu thụ.
3.2. Hàm phân bố Weibull trong trường hợp chung có dạng:
F(t,a,b,c) = 1-exp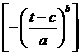
0 ≤ c < t < + ¥; a > 0; b > 0
trong đó: a – tham số tỉ lệ
b – tham số dạng
c – tham số định vị
Tiêu chuẩn này áp dụng cho trường hợp tham số định vị c = 0 nên hàm phân bố có dạng:
F(t,a,b) = 1-exp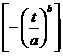
t ≥ 0; a > 0; b > 0
Nếu tham số c khác không và đã biết thì trong các bảng và sơ đồ các phương án kiểm tra của tiêu chuẩn này t1 (là thời gian thử nghiệm cho trước) được thay bằng t1' = t1 - c và t0' = t0 -c (t0 là thời gian làm việc không hỏng trung bình cho trước). Cường độ hư hỏng có dạng:
l(t,a,b)=![]()
t ≥ 0; a > 0; b > 0
Có thể xác định cường độ hư hỏng bằng phương pháp thống kê căn cứ vào số sản phẩm hỏng trong một đơn vị thời gian và số sản phẩm thử nghiệm.
3.3. Các phương án kiểm tra của tiêu chuẩn này được thiết lập theo cường độ hư hỏng với tham số b của hàm Weibull đã biết và tham số c = 0.
3.4. Trong tiêu chuẩn này việc kiểm tra độ tin cậy của lô sản phẩm so với yêu cầu đã định được thực hiện theo phương pháp kiểm tra mẫu. Chất lượng của lô được đặc trưng bằng tỉ lệ sản phẩm hỏng p (tức là các sản phẩm không thỏa mãn yêu cầu về thời gian làm việc không hỏng).
Phương pháp kiểm tra mẫu ở đây đảm bảo khi p = AQL / 100 thì xác suất chấp nhận lô là cao, còn với lô có mức hư hỏng tại mức bác bỏ LQ thì xác suất chấp nhận không lớn hơn b = 0,1.
Giá trị AQL là giá trị đầu vào và trong kiểm tra mẫu là mức hư hỏng lớn nhất được phép nghiệm thu và cũng là mức hư hỏng trung bình của lô. Giá trị LQ là giá trị thông báo.
Kết luận về độ tin cậy của lô N sản phẩm được căn cứ vào kết quả thử nghiệm của sản phẩm lấy ngẫu nhiên trong lô N. Các sản phẩm được thử nghiệm trong khoảng thời gian t1 bằng thời gian làm việc không hỏng trung bình t0 hoặc ngắn hơn. Trong quá trình thử nghiệm số sản phẩm hỏng r được xác định.
Phương án kiểm tra nghiệm thu về độ tin cậy ở đây được xác định bằng ba thông số n, Ac, t1. Trong đó Ac là số chấp nhận. Việc chọn phương án kiểm tra phụ thuộc vào yêu cầu cho trước về AQL và cường độ hư hỏng l(t). Thiết lập quan hệ giữa tỉ lệ sản phẩm hỏng p của lô và cường độ hư hỏng l(t):
t x l(t) = b x ln (1 – p)
Để giảm nhẹ việc tính toán, các bảng của tiêu chuẩn này cho các giá trị 100tl(t). Nếu giá trị tính toán được không có trong bảng thì chọn giá trị bé hơn gần nhất.
4.1. Các phương án kiểm tra trong tiêu chuẩn này được thiết lập với mức chất lượng chấp nhận AQL = 0,01; 0,015; 0,025; 0,04; 0,065; 0,1; 0,15; 0,25; 0,4; 0,65; 1,0; 1,5; 4; 6,5; 10 và biểu thị bằng phần trăm. Tham số dạng b có các giá trị 1/3; 1/2; 1; 4/3; 5/3; 2; 5/2; 10/3; 4. Mức rủi ro a = 0,05 và b = 0,1.
Trị số AQL phải được cho trong chỉ dẫn kỹ thuật của sản phẩm hoặc trong hợp đồng.
4.2. Để kết luận về lô sản phẩm cần kiểm tra, phải tiến hành các bước từ 4.2.1 đến 4.2.4.
4.2.1. Trên cơ sở các đại lượng đã biết và theo các bảng từ 1 đến 4, xác định phương án kiểm tra tương ứng để có số liệu về n và Ac.
4.2.2. Từ lô lấy ngẫu nhiên n sản phẩm và đưa vào thử nghiệm ở chế độ đã chọn trước trong khoảng thời gian ấn định t1.
4.2.3. Xác định số sản phẩm hỏng r trong khoảng thời gian thử nghiệm t1. So sánh trị số r với trị số chấp nhận Ac của phương án kiểm tra.
4.2.4. Lô sản phẩm được chấp nhận nếu r ≤ Ac và không được chấp nhận khi r ≥ Ac + 1.
4.3. Các phương án kiểm tra được trình bày theo các sơ đồ. Trong các sơ đồ này việc xác định các đại lượng của phương án kiểm tra được đánh dấu bằng đường đậm nét, còn các đại lượng phụ bằng các đường nét đứt. Các ví dụ về sử dụng các phương án này cho trong Phụ lục A.
4.3.1. Trường hợp 1: thời gian thử nghiệm bằng thời gian làm việc trung bình không hỏng (t1 = t0)
4.3.1.1. Phương án 1:
Những đại lượng đã biết: N, t0, l(t0). Những đại lượng phải xác định:
– Đại lượng của phương án kiểm tra: n, Ac;
– Đại lượng phụ l(2(t0), LQ.
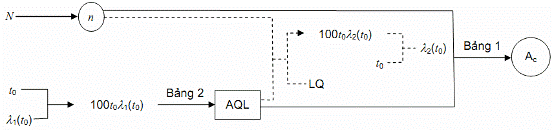
Hình 1 – Sơ đồ 1
4.3.1.2. Phương án 2:
Những đại lượng đã biết: N, t0, l2(t0).
Những đại lượng phải xác định:
– Đại lượng của phương án kiểm tra: n, Ac;
– Đại lượng phụ l1(t0), LQ.
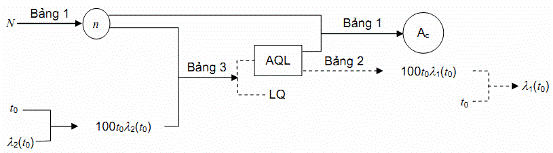 Hình 2 – Sơ đồ 2
Hình 2 – Sơ đồ 2
4.3.1.3. Phương án 3:
Những đại lượng đã biết: t0, l1(t0), l2(t0).
Những đại lượng phải xác định:
– Đại lượng của phương án kiểm tra: n, Ac;
– Đại lượng phụ N, LQ.
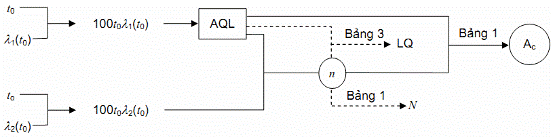
Hình 3 – Sơ đồ 3
4.3.1.4. Phương án 4:
Những đại lượng đã biết: N, t0, AQL.
Những đại lượng phải xác định:
– Đại lượng của phương án kiểm tra: n, Ac;
– Đại lượng phụ l1(t0), l2(t0), LQ.
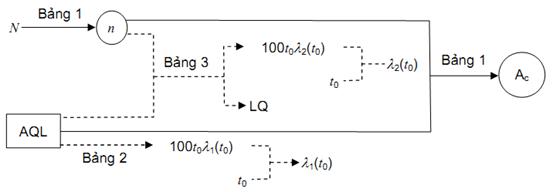
Hình 4 – Sơ đồ 4
4.3.1.5. Phương án 5:
Những đại lượng đã biết: N, t0, LQ.
Những đại lượng phải xác định:
– Đại lượng của phương án kiểm tra: n, Ac;
– Đại lượng phụ l1(t0); l2(t0).

Hình 5 – Sơ đồ 5
4.3.2. Trường hợp 2: thời gian thử nghiệm t1 nhỏ hơn thời gian làm việc không hỏng t0
4.3.2.1. Phương án 6:
Những đại lượng đã biết: N, t0, t1, l1(t0).
Những đại lượng phải xác định:
– Đại lượng của phương án kiểm tra: n, Ac;
– Đại lượng phụ: l2(t0), AQL, LQ.
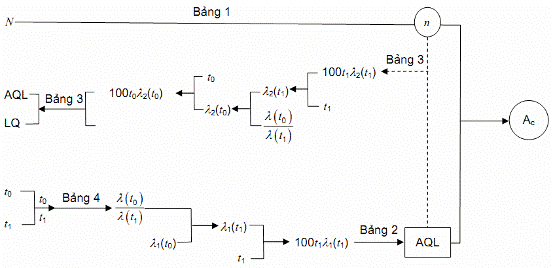
Hình 6 – Sơ đồ 6
4.3.2.2. Phương án 7:
Những đại lượng đã biết: N, t0, t1, l2(t0).
Những đại lượng phải xác định:
– Đại lượng của phương án kiểm tra: n, Ac;
– Đại lượng phụ: l1(t0), AQL, LQ.
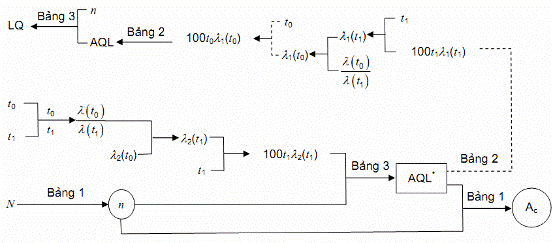
Hình 7 – Sơ đồ 7
4.3.2.3. Phương án 8:
Những đại lượng đã biết: t0, t1, l2(t0).
Những đại lượng phải xác định:
– Đại lượng của phương án kiểm tra: n, Ac;
– Đại lượng phụ: N, l1(t0), AQL, LQ.
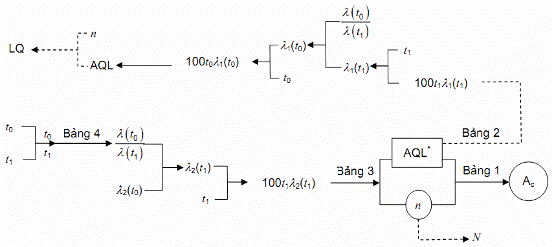
Hình 8 – Sơ đồ 8
Bảng 1 – Cỡ mẫu n và số chấp nhận Ac tùy thuộc vào N và AQL
| N | n | AQL % | |||||||||||||||||||||||||||||||
| 0,01 | 0,015 | 0,025 | 0,04 | 0,065 | 0,10 | 0,15 | 0,20 | 0,40 | 0,65 | 1,0 | 1,5 | 2,5 | 4,0 | 6,5 | 10 | ||||||||||||||||||
| 2 – 8 | 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ↓ | 0 |
|
| ||
| 9 – 15 | 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ↓ | 0 |
|
| ↓ | |||
| 16 – 25 | 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ↓ | 0 |
|
| ↓ | 1 | ||||
| 26 – 50 | 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ↓ | 0 |
|
| ↓ | 1 | 2 | |||||
| 51 – 90 | 13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ↓ | 0 |
|
| ↓ | 1 | 2 | 3 | ||||||
| 91 – 150 | 20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ↓ | 0 |
|
| ↓ | 1 | 2 | 3 | 5 | |||||||
| 151 – 280 | 32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ↓ | 0 |
|
| ↓ | 1 | 2 | 3 | 5 | 7 | ||||||||
| 281 – 500 | 50 |
|
|
|
|
|
|
|
|
|
|
|
| ↓ | 0 |
|
| ↓ | 1 | 2 | 3 | 5 | 7 | 10 | |||||||||
| 501 – 1 200 | 80 |
|
|
|
|
|
|
|
|
|
| ↓ | 0 |
|
| ↓ | 1 | 2 | 3 | 5 | 7 | 10 | 14 | ||||||||||
| 1 201 – 3 200 | 125 |
|
|
|
|
|
|
|
| ↓ | 0 |
|
| ↓ | 1 | 2 | 3 | 5 | 7 | 10 | 14 | 21 | |||||||||||
| 3 201 – 10 000 | 200 |
|
|
|
|
|
| ↓ | 0 |
|
| ↓ | 1 | 2 | 3 | 5 | 7 | 10 | 14 | 21 | ↑ | ||||||||||||
| 10 001 – 35 000 | 315 |
|
|
|
| ↓ | 0 |
|
| ↓ | 1 | 2 | 3 | 5 | 7 | 10 | 14 | 21 | ↑ |
|
| ||||||||||||
| 35 001 – 150 000 | 500 |
|
| ↓ | 0 | ↑ | ↓ | 1 | 2 | 3 | 5 | 7 | 10 | 14 | 21 | ↑ |
|
|
|
| |||||||||||||
| 150 001 – 500 000 | 800 | ↓ | 0 | ↑ | ↓ | 1 | 2 | 3 | 5 | 7 | 10 | 14 | 21 | ↑ |
|
|
|
|
|
| |||||||||||||
| 500 001 ... | 1 250 | 0 | ↑ | 1 | 1 | 2 | 3 | 5 | 7 | 10 | 14 | 21 | ↑ |
|
|
|
|
|
|
|
| ||||||||||||
Bảng 2 – Giá trị 100tl1(t) tùy thuộc vào AQL và b
| AQL % | b | |||||||||
| 1/3 | 1/2 | 2/3 | 1 | 4/3 | 5/3 | 2 | 5/2 | 10/3 | 4 | |
| 0,010 | 0,003 3 | 0,005 5 | 0,006 7 | 0,010 | 0,013 | 0,017 | 0,020 | 0,025 | 0,037 | 0,040 |
| 0,015 | 0,005 0 | 0,007 6 | 0,010 | 0,015 | 0,020 | 0,025 | 0,030 | 0,038 | 0,050 | 0,060 |
| 0,025 | 0,008 3 | 0,012 | 0,017 | 0,025 | 0,033 | 0,042 | 0,050 | 0,063 | 0,08 | 0,10 |
| 0,040 | 0,013 | 0,020 | 0,027 | 0,040 | 0,053 | 0,067 | 0,080 | 0,10 | 0,13 | 0,16 |
| 0,065 | 0,022 | 0,032 | 0,043 | 0,065 | 0,087 | 0,11 | 0,13 | 0,16 | 0,22 | 0,26 |
| 0,10 | 0,033 | 0,050 | 0,067 | 0,10 | 0,13 | 0,17 | 0,20 | 0,25 | 0,33 | 0,40 |
| 0,15 | 0,050 | 0,075 | 0,10 | 0,15 | 0,20 | 0,25 | 0,30 | 0,38 | 0,56 | 0,60 |
| 0,25 | 0,083 | 0,13 | 0,17 | 0,25 | 0,33 | 0,42 | 0,50 | 0,63 | 0,83 | 1,00 |
| 0,40 | 0,13 | 0,20 | 0,27 | 0,40 | 0,54 | 0,67 | 0,80 | 1,00 | 1,34 | 1,60 |
| 0,65 | 0,22 | 0,33 | 0,44 | 0,65 | 0,87 | 1,09 | 1,30 | 1,63 | 2,17 | 2,81 |
| 1,0 | 0,34 | 0,50 | 0,67 | 1,01 | 1,34 | 1,68 | 2,01 | 2,51 | 3,85 | 4,02 |
| 1,5 | 0,50 | 0,76 | 1,01 | 1,51 | 2,02 | 2,52 | 3,02 | 3,78 | 5,04 | 6,04 |
| 2,5 | 0,84 | 1,27 | 1,69 | 2,53 | 2,38 | 4,22 | 5,06 | 6,33 | 8,44 | 10,1 |
| 4,0 | 1,36 | 2,04 | 2,72 | 4,08 | 5,44 | 6,80 | 8,16 | 10,2 | 13,6 | 16,3 |
| 6,5 | 2,24 | 3,36 | 4,43 | 6,72 | 8,96 | 11,2 | 13,4 | 16,8 | 22,4 | 26,9 |
| 10 | 3,51 | 5,27 | 7,02 | 10,5 | 14 | 17,6 | 21,1 | 26,3 | 35,1 | 41,1 |
Bảng 3 – Giá trị 100t2l(t) tùy thuộc vào n, AQL, LQ với mỗi giá trị b khác nhau
| n | AQL (%) | LQ (%) | b | |||||||||
| 1/3 | 1/2 | 2/3 | 1 | 4/3 | 5/3 | 2 | 5/2 | 10/3 | 4 | |||
| 2 | 6,5 | 68,4 | 37 | 54 | 76 | 110 | 150 | 180 | 220 | 280 | 379 | 470 |
| 3 | 4,0 | 53,6 | 25 | 38 | 50 | 77 | 100 | 130 | 150 | 190 | 260 | 310 |
| 5 | 2,5 10 | 36,9 58,4 | 15 28 | 22 43 | 30 57 | 46 86 | 61 110 | 76 140 | 92 170 | 110 210 | 150 290 | 180 350 |
| 8 | 1,5 6,5 10 | 25,0 40,6 53,9 | 9,6 17 25 | 14 26 38 | 19 35 50 | 29 53 77 | 38 71 100 | 48 88 130 | 57 100 150 | 72 130 190 | 96 170 260 | 110 210 310 |
| 15 | 1,0 4,0 6,5 10 | 16,2 26,8 36,0 44,4 | 5,8 10 14 19 | 8,7 15 22 28 | 11 21 29 38 | 17 31 45 59 | 23 40 62 77 | 29 53 75 97 | 35 63 90 110 | 42 78 110 140 | 58 100 150 190 | 70 100 180 230 |
| 20 | 0,55 2,5 4,0 6,5 10 | 10,9 18,1 24,5 30,4 41,5 | 3,0 6,5 9,6 30,4 41,5 | 5,7 9,9 14 18 27 | 7,8 13 19 24 36 | 11 20 28 36 54 | 15 26 38 47 73 | 19 33 48 59 92 | 23 40 57 71 110 | 29 50 72 89 130 | 38 66 96 120 180 | 47 80 110 140 220 |
| 32 | 0,40 1,5 2,5 4,0 6,5 10 | 0,94 11,6 15,8 19,7 27,1 34,1 | 2,3 4,3 5,8 7,4 10 13 | 3,5 4,6 8,7 11 15 20 | 4,7 8,5 11 15 21 27 | 7,2 13 17 22 31 42 | 9,5 17 23 30 42 58 | 12 21 29 37 53 70 | 14 25 35 44 63 85 | 18 32 42 56 78 100 | 23 42 58 74 100 140 | 28 51 70 89 120 170 |
| 50 | 0,25 1,0 1,5 2,5 4,0 6,5 10 | 4,50 7,56 10,3 12,9 17,8 22,4 29,1 | 1,5 2,6 3,5 4,7 6,6 8,3 11 | 2,3 3,9 5,2 6,9 9,9 12 17 | 3 5,3 7 9,3 13 16 22 | 4,6 7,9 10 14 20 25 34 | 0,1 10 14 18 26 33 46 | 7,6 13 17 23 33 41 57 | 9,3 16 21 28 40 50 69 | 11 19 26 35 50 62 86 | 15 26 35 46 66 81 110 | 18 31 42 56 80 100 130 |
| 80 | 0,15 0,65 1,0 1,5 2,5 4,0 6,5 10 | 2,84 4,78 6,52 8,16 11,3 14,2 18,6 24,2 | 0,95 1,6 2,2 2,8 3,9 5 7 9,9 | 1,4 2,4 3,3 4,2 5,7 7,5 10 13 | 1,8 3,2 4,5 5,7 7,8 10 14 18 | 2,8 4,9 6,7 8,6 14 15 21 27 | 3,7 6,5 8,9 11 15 20 28 36 | 4,7 8,8 11 14 19 25 34 45 | 5,7 9,9 13 17 23 30 42 55 | 7,1 12 17 21 29 37 53 69 | 9,5 16 22 28 38 50 70 90 | 11 19 27 34 47 61 86 110 |
| 125 | 0,10 0,40 0,65 1,0 1,5 2,5 4,0 6,5 10 | 1,84 3,10 4,26 5,35 7,42 9,42 12,3 16,1 22,5 | 0,60 1 1,4 1,8 2,5 3,2 4,2 5,8 8,7 | 0,90 1,5 2,2 2,7 3,8 4,9 6,4 8,7 13 | 1,2 2 2,9 3,6 5,1 6,6 8,5 11 17 | 1,9 3,2 4,4 5,6 7,6 9,9 13 18 25 | 2,4 4,2 5,8 7,3 10 13 17 23 35 | 3 5,3 7,3 9,2 13 16 21 29 43 | 3,6 6,3 8,9 11 15 19 25 35 53 | 4,5 7,8 11 13 19 23 32 42 66 | 6 10 14 18 25 32 42 58 86 | 7,2 12 17 21 30 39 51 70 100 |
| 200 | 0,065 0,25 0,40 0,65 1,0 1,5 2,5 4,0 6,5 | 1,15 1,95 2,66 3,34 4,64 5,89 7,70 10,1 14,1 | 0,40 0,67 0,91 1,1 1,5 2 2,6 3,5 5 | 0,60 1 1,3 1,6 2,3 3 3,9 5,2 7,5 | 0,80 1,3 1,8 2,2 3,1 4 5,3 7 10 | 1,2 2 2,7 3,4 4,8 6,1 8 11 15 | 1,6 2,7 3,6 4,4 6,3 8,4 10 14 20 | 2 3,3 4,6 5,5 7,8 10 13 17 25 | 2,4 4,0 5,5 6,7 9,5 12 16 21 30 | 3 5 6,8 8,4 11 15 20 26 37 | 4 6,7 9,1 11 15 20 26 35 50 | 4,8 8,1 11 13 19 24 32 42 61 |
| 315 | 0,010 0,15 0,25 0,40 0,65 1,0 1,5 2,5 4,0 | 0,731 1,23 1,69 2,12 2,94 3,74 4,89 6,09 8,95 | 0,25 0,40 0,56 0,70 0,98 1,2 1,6 2,2 3,1 | 0,36 0,66 0,84 1 1,4 1,9 2,5 3,3 4,6 | 0,49 0,80 1,1 1,4 1,9 2,5 3,3 4,4 6,3 | 0,73 1,2 1,7 2,1 3,0 3,8 5 6,6 9,4 | 0,96 1,6 2,3 2,8 3,9 5 6,7 8,7 12 | 1,2 2 2,8 3,5 4,9 6,7 8,4 11 15 | 1,4 2,4 3,4 4,2 6 7,6 10 13 19 | 1,8 3 4,2 5,3 7,4 9,4 12 16 23 | 2,4 4 5,7 7 9,8 12 16 21 31 | 2,9 4,8 6,8 8,5 11 15 20 26 38 |
| 500 | 0,025 0,10 0,15 0,25 0,40 0,65 1,0 1,5 2,5 | 0,461 0,778 1,06 1,34 1,86 2,35 3,08 4,03 5,64 | 0,15 0,26 0,37 0,44 0,63 0,80 1 1,3 1,9 | 0,23 0,39 0,55 0,65 0,95 1,2 1,5 2 2,8 | 0,31 0,52 0,74 0,88 1,2 1,6 2 2,7 3,8 | 0,46 0,78 1,1 1,3 1,9 2,4 3,1 4,1 5,8 | 0,60 1 1,4 1,7 2,5 3,2 4,2 5,4 7,7 | 0,70 1,3 1,8 2,2 3,2 4 5,3 6,8 9,5 | 0,92 1,5 2,2 2,6 3,8 4,8 6,3 8,1 11 | 1,1 1,9 2,7 3,2 4,8 6 7,8 10 14 | 1,5 2,6 3,7 4,4 6,3 8,1 10 13 19 | 1,8 3,1 4,4 5,2 7,6 9,7 12 16 23 |
| 800 | 0,015 0,065 0,10 0,15 0,25 0,40 0,65 1,0 1,5 | 0,288 0,486 0,665 0,835 1,06 1,47 1,93 2,52 3,52 | 0,096 0,16 0,22 0,28 0,40 0,50 0,64 0,84 1,2 | 0,14 0,24 0,33 0,42 0,60 0,75 0,95 1,2 1,8 | 0,19 0,32 0,45 0,56 0,80 1 1,3 1,6 2,3 | 0,29 0,49 0,67 0,84 1,2 1,5 1,9 2,5 3,5 | 0,36 0,65 0,89 1,1 1,6 2 2,5 3,3 4,7 | 0,48 0,81 1,1 1,4 2 2,5 3,2 4,2 6 | 0,58 0,98 1,3 1,7 2,4 3 3,8 5 7,2 | 0,72 1,2 1,6 2,1 3 3,7 4,8 6,3 8,9 | 0,95 1,6 2,2 2,8 4 5 6,4 8,4 12 | 1,1 1,9 2,7 3,4 4,8 6 7,6 10 14 |
| 1 250 | 0,010 0,040 0,10 0,15 0,25 0,40 0,68 1,0 | 0,181 0,310 0,534 0,742 0,942 1,23 1,61 2,25 | 0,06 0,10 0,17 0,25 0,33 0,40 0,54 0,77 | 0,09 0,15 0,26 0,37 0,47 0,60 0,80 1,1 | 0,12 0,20 0,35 0,50 0,63 0,80 1,1 1,5 | 0,18 0,31 0,53 0,74 0,94 1,2 1,6 2,3 | 0,24 0,40 0,70 0,97 1,2 1,6 2,1 3,1 | 0,30 0,51 0,87 1,2 1,5 2 2,7 3,9 | 0,30 0,62 1 1,4 1,9 2,4 3,2 4,7 | 0,45 0,77 1,3 1,8 2,3 3 4 5,8 | 0,60 1 1,7 2,4 3,2 4 5,4 7,7 | 0,71 1,2 2,1 3 3,8 4,8 6,4 9,3 |
Bảng 4 – Tỷ số l(t0)/l(t1) đối với mỗi t0/t1 và b
|
| b | |||||||||
| 1/3 | 1/2 | 2/3 | 1 | 4/3 | 5/3 | 2 | 5/2 | 10/3 | 4 | |
| 1,25 | 0,862 | 0,894 | 0,928 | 1,00 | 1,08 | 1,16 | 1,25 | 1,40 | 1,68 | 2,95 |
| 1,50 | 0,760 | 0,816 | 0,873 | 1,00 | 1,14 | 1,31 | 1,50 | 1,84 | 1,57 | 3,30 |
| 1,75 | 0,689 | 0,756 | 0,823 | 1,00 | 1,21 | 1,45 | 1,75 | 2,32 | 2,69 | 5,36 |
| 2,00 | 0,630 | 0,707 | 0,794 | 1,00 | 1,26 | 1,59 | 2,00 | 2,88 | 5,84 | 8,00 |
| 2,25 | 0,583 | 0,667 | 0,763 | 1,00 | 1,31 | 1,72 | 2,25 | 3,38 | 6,64 | 11,4 |
| 2,50 | 0,543 | 0,632 | 0,734 | 1,00 | 1,36 | 1,84 | 2,50 | 3,95 | 8,49 | 15,6 |
| 2,75 | 0,510 | 0,603 | 0,714 | 1,00 | 1,40 | 1,96 | 2,75 | 4,56 | 10,6 | 20,8 |
| 3,00 | 0,481 | 0,677 | 0,694 | 1,00 | 1,44 | 2,08 | 3,00 | 5,20 | 13,0 | 27,0 |
| 3,25 | 0,456 | 0,555 | 0,675 | 1,00 | 1,48 | 2,19 | 3,25 | 6,86 | 15,6 | 34,3 |
| 3,50 | 0,434 | 0,534 | 0,659 | 1,00 | 1,52 | 2,30 | 3,50 | 6,55 | 18,4 | 42,9 |
| 3,75 | 0,414 | 0,516 | 0,644 | 1,00 | 1,55 | 2,42 | 3,75 | 7,26 | 21,8 | 52,7 |
| 4,00 | 0,397 | 0,500 | 0,630 | 1,00 | 1,59 | 2,52 | 4,00 | 8,00 | 25,4 | 64,0 |
| 4,25 | 0,381 | 0,485 | 0,617 | 1,00 | 1,62 | 2,62 | 4,25 | 8,76 | 29,3 | 76,8 |
| 4,50 | 0,367 | 0,472 | 0,606 | 1,00 | 1,65 | 2,73 | 4,50 | 9,54 | 33,4 | 91,1 |
| 4,75 | 0,354 | 0,459 | 0,595 | 1,00 | 1,68 | 2,83 | 4,75 | 10,4 | 37,9 | 107 |
| 5,00 | 0,342 | 0,447 | 0,585 | 1,00 | 1,71 | 2,92 | 5,00 | 11,2 | 42,8 | 125 |
A.1. Ví dụ 1: Sử dụng phương án kiểm tra theo sơ đồ 1
Xác định phương án kiểm tra khi cho trước N = 700 sản phẩm, t0 = 800 h, l1(t0)=0,000 008 3, hàm phân bố thời gian làm việc đến hỏng là Weibull có tham số dạng b = 2/3.
Xác định các đại lượng của phương án kiểm tra:
– Từ Bảng 1, với N = 700 tìm được n = 80.
– Với t0 và l1(t0) đã biết tính được 100t0l1(t0) = 100 x 800 x 0,000 008 3 = 0,664.
– Từ Bảng 2 với b = 2/3, giá trị gần 0,664 nhất là 0,67 và AQL = 1 %.
– Từ Bảng 1, với AQL = 1 % và n = 80 tìm được Ac = 2.
Kết luận: Lấy ngẫu nhiên 80 sản phẩm từ lô cần kiểm tra. Những sản phẩm này được đưa vào thử nghiệm trong khoảng thời gian 800 h. Xác định số sản phẩm hỏng r trong thời gian này. Lô sản phẩm được chấp nhận nếu r ≤ 2 và bị bác bỏ nếu r ≥ 3.
Xác định các đại lượng phụ:
– Từ Bảng 3, với n = 80 và AQL = 1 %, tìm được 100t0l2(t0) = 4,5, với t0 = 800 h, tính được:
l2(t0) =![]() = 0,000 056 2
= 0,000 056 2
– Từ Bảng 3, với n = 80 và AQL = 1 %, tìm được LQ = 6,52 %.
A.2. Ví dụ 2: Sử dụng phương án kiểm tra theo sơ đồ 2
Xác định phương án kiểm tra khi cho trước N = 2 000 sản phẩm, t0 = 1 000 h, l2(t0)= 0,000 1, hàm phân bố thời gian làm việc không hỏng là Weibull có tham số dạng b = 4/5.
Xác định các đại lượng của phương án kiểm tra:
– Từ Bảng 1, với N = 2 000 tìm được n = 125.
– Với t0 = 1 000 h và l2(t0) = 0,000 1, tính được:
100t0l2(t0) = 100 x 1 000 x 0,000 1 = 10.
– Từ Bảng 3 với b = 4/3, 100t0l2(t0) = 10 và n = 125, tìm được AQL = 1,5 %.
– Từ Bảng 1, với AQL = 1,5 % và n = 125, tìm được Ac = 5.
Kết luận: Từ lô sản phẩm cần kiểm tra, lấy ngẫu nhiên n = 125 sản phẩm, những sản phẩm này được đưa vào thử nghiệm trong khoảng thời gian t0 = 1 000 h. Xác định số sản phẩm hỏng r trong thời gian này. Lô sản phẩm được chấp nhận nếu r ≤ 5 và bị bác bỏ nếu r ≥ 6.
Xác định các đại lượng phụ:
– Từ Bảng 3, với b = 4/3 và AQL = 1,5 %, tìm được 100t0l1(t0) = 2,02, từ đó tính được:
l1(t0) =![]() = 0, 000 020 2
= 0, 000 020 2
– Từ Bảng 3, với n = 125 và AQL = 1,5 %, tìm được LQ = 7,42 %.
A.3. Ví dụ 3: Sử dụng phương án kiểm tra theo sơ đồ 3
Xác định phương án kiểm tra khi cho trước t0=700 h, l1(t0) = 0,000 057 4, l2(t0)=0,000 271 4. Hàm phân bố thời gian làm việc không hỏng là Weibull có tham số dạng b = 4.
Xác định các đại lượng của phương án kiểm tra:
– Với t0 = 700 h và l1(t0) = 0,000 057 4, tính được:
100t0l1(t0) = 100 x 700 x 0,000 057 4 = 4,02.
– Từ Bảng 2 với giá trị 4,02 và b = 4 , tìm được AQL = 1 %.
– Với t0 = 700 h và l2(t0) = 0,000 271 4, tính được:
100t0l2(t0) = 100 x 700 x 0,000 271 4 = 19.
Theo Bảng 3 với AQL = 1 %, 100t0l2(t0) = 19 và b = 4, tìm được n = 200.
– Từ Bảng 1, với n = 200, AQL = 1 %, tìm được Ac = 5.
Kết luận: Lấy ngẫu nhiên n = 200 sản phẩm, đem thử nghiệm trong khoảng thời gian t0 = 700 h. Xác định số sản phẩm hỏng r. Lô được coi là chấp nhận nếu r ≤ 5 và bị bác bỏ nếu r ≥ 6.
Xác định các đại lượng phụ:
– Theo Bảng 4, khi AQL = 1 % và n = 200, tìm được LQ = 4,64 %.
A.4. Ví dụ 4: Sử dụng phương án kiểm tra theo sơ đồ 4
Xác định phương án kiểm tra khi biết trước N = 250 sản phẩm, hàm phân bố thời gian làm việc không hỏng là Weibull có tham số dạng b = 5/2, cho AQL = 2,5 % và t0 = 1 500 h.
Xác định các đại lượng của phương án kiểm tra:
– Từ Bảng 1, với N = 250, tìm được n = 32.
– Từ Bảng 1 với n = 32 và AQL = 2,5 %, tìm được Ac = 2.
Kết luận: Từ lô sản phẩm phải kiểm tra, lấy ngẫu nhiên n = 32 sản phẩm đưa thử nghiệm, trong khoảng thời gian t0 = 1 500 h xác định số sản phẩm hỏng r. Lô được chấp nhận nếu r ≤ 2 và bị bác bỏ nếu r ≥ 3.
Xác định các đại lượng phụ:
– Theo Bảng 2, với AQL = 2,5 % và b = 5/2, tìm được giá trị 100t0l1(t0) = 6,33.
l1(t0) =![]() = 0, 000 042 2
= 0, 000 042 2
– Theo Bảng 3, với n = 32 và AQL = 2,5 %, tìm được LQ = 15,8 % và khi b = 5/2 tìm được giá trị 100t0l2(t0) = 42. Từ đó tính được:
l2(t0) =![]() = 0, 000 28
= 0, 000 28
A.5. Ví dụ 5: Sử dụng phương án kiểm tra theo sơ đồ 5
Xác định phương án kiểm tra khi biết trước N = 1 500, LQ = 7,42 % và t0 = 1 000 h. Hàm phân bố thời gian làm việc không hỏng là hàm Weibull với tham số dạng b = 10/3.
Xác định các đại lượng của phương án kiểm tra:
– Từ Bảng 1, với N = 1 500 tìm được n = 125.
– Từ Bảng 3 với n = 125 và LQ = 7,42 tìm được AQL = 1,5 %.
– Từ Bảng 1, với AQL = 1,5 % và n = 125 tìm được Ac = 5.
Kết luận: Từ lô sản phẩm phải kiểm tra, lấy ngẫu nhiên n = 125 sản phẩm đưa thử nghiệm trong khoảng t0 = 1 000 h. Xác định số sản phẩm hỏng r. Lô được chấp nhận nếu r ≤ 5 và bị bác bỏ nếu r ≥ 6.
Xác định các đại lượng phụ:
– Theo Bảng 2, với AQL = 1,5 % tìm được giá trị 100t0l1(t0) = 5,04.
l1(t0) =![]() = 0,000 050 4
= 0,000 050 4
A.6. Ví dụ 6: Sử dụng phương án kiểm tra theo sơ đồ 6
Xác định phương án kiểm tra cho lô N = 12 000 sản phẩm. Cường độ hư hỏng được xác lập sau t0 = 1 000 h là l1(t0) = 0,000 025. Hàm phân bố thời gian làm việc không hỏng là hàm Weibull với tham số dạng b = 5/2, thời gian thử nghiệm t1 = 500 h.
Xác định các đại lượng của phương án kiểm tra:
– Đối với t0 = 1 000 h, t1 = 500 h tính được ![]() = 2.
= 2.
– Theo Bảng 4, với ![]() = 2 và b = 5/2 tìm được
= 2 và b = 5/2 tìm được ![]() = 2, 83.
= 2, 83.
– Với l1(t0) và ![]() = 2, 83 tính được
= 2, 83 tính được
l1(t1) = ![]() = 0,000 008 8
= 0,000 008 8
– Với l1(t1) và t1 tính được
100t1l1(t1) = 100 x 500 x 0,000 008 8 = 0,44.
– Theo Bảng 2, giá trị gần với 0,44 nhất đối với b = 5/2 là 0,38, từ đó tìm được AQL* = 0,15%.
– Theo Bảng 1, với N = 12 000 tương ứng n = 315 và Ac = 1 khi giá trị AQL* = 0,15 %.
Kết luận: lấy ngẫu nhiên n = 315 sản phẩm từ lô phải kiểm tra, tiến hành thử nghiệm trong khoảng t1 = 500 h, xác định số sản phẩm hỏng r. Lô được chấp nhận nếu r ≤ 1 và bị bác bỏ nếu r ≥ 2. Xác định các đại lượng phụ:
– Theo Bảng 3, với AQL* = 0,15 %, n = 315 và b = 5/2 tìm được giá trị 100t1l2(t1) = 3, từ đó
l2(t1) = ![]() = 0,000 06
= 0,000 06
– Từ Bảng 4 có![]() = 2,83 tính được
= 2,83 tính được
l2(t0) = l2(t1) x 2,83 = 0,000 169 8
– Từ t0 và l2(t0) tính được 100t0l2(t0) = 100 x 1 000 x 0,000 169 8 = 16,98.
– Theo Bảng 3, với b = 5/2, n = 315, giá trị gần với 16,98 nhất là 16, giá trị này tương ứng với AQL* = 2,5 % và LQ = 6,3 %.
A.7. Ví dụ 7: Sử dụng phương án kiểm tra theo sơ đồ 7
Cần xác định phương án kiểm tra cho lô sản phẩm N = 450, cường độ hư hỏng bác bỏ trong thời gian làm việc không hỏng trung bình t0 = 1 000 h có giá trị l2(t0) = 0,000 59, thời gian thử nghiệm cho trước t1 = 600 h. Hàm phân bố thời gian làm việc không hỏng là hàm Weibull với tham số dạng b = 5/3.
Xác định các đại lượng của phương án kiểm tra:
– Theo Bảng 1, với N = 450 tìm được n = 50.
– Trên cơ sở t0 = 1 000 h, t1 = 600 h tính được ![]() = 1, 66.
= 1, 66.
– Theo Bảng 4, giá trị gần với 1,66 là 1,75 tương ứng khi b=5/3, từ đó tìm được ![]() =1, 45 – Trên cơ sở
=1, 45 – Trên cơ sở ![]() =1,45 và l2(t0) = 0,000 59 tính được
=1,45 và l2(t0) = 0,000 59 tính được
l2(t1) = ![]() = 0, 000 41.
= 0, 000 41.
– Trên cơ sở t1 = 600 h và l2(t1) = 0,000 41 tính được
100t1l2(t1) = 100 x 600 x 0,000 41 = 24,6.
– Theo Bảng 3, giá trị gần với 24,6 nhất là 23 tương ứng với n = 50 và b = 5/3, từ những giá trị này tìm được AQL = 2,5 % và Ac = 3.
Kết luận: lấy ngẫu nhiên n = 50 sản phẩm từ lô cần kiểm tra, đưa thử nghiệm trong khoảng thời gian t1 = 600 h, xác định số sản phẩm hỏng r. Lô được chấp nhận nếu r ≤ 3 và bị bác bỏ nếu r ≥ 4. Xác định các đại lượng phụ:
– Theo Bảng 2, khi AQL* = 2,5 % và b = 5/3, tìm được 100t1l1(t1) = 4,22 nên tính được
l1(t1) = ![]() = 0, 000 07.
= 0, 000 07.
– Trên cơ sở ![]() =1,45 và l1(t1) = 0,000 07 tính được
=1,45 và l1(t1) = 0,000 07 tính được
l1(t0) = 1,45 x 0,000 07 = 0,000 1.
– Trên cơ sở l1(t0) = 0,000 1 và t0 = 1 000 h tính được
100t0l1(t0) = 100 x 1 000 x 0,000 1 = 10.
– Theo Bảng 2, với b = 5/3 và AQL = 6,5 % tìm được giá trị LQ = 22,4 %.
A.8. Ví dụ 8: Sử dụng phương án kiểm tra theo sơ đồ 8
Cần xác định phương án kiểm tra của lô sản phẩm có cường độ hư hỏng bác bỏ là l2(t0) = 0,000 78, thời gian làm việc không hỏng trung bình t0 = 1 500 h. Thời gian thử nghiệm cho trước t1 = 850 h. Hàm phân bố thời gian làm việc không hỏng là hàm Weibull có tham số dạng b = 2.
Xác định các đại lượng của phương án kiểm tra:
– Trên cơ sở t0 = 1 500 h, t1 = 850 h tính được ![]() = 1, 76.
= 1, 76.
– Theo Bảng 4 giá trị gần với 1,76 nhất là 1,75. Trên cơ sở này tính được ![]() = 1,75 với b=2
= 1,75 với b=2
Đồng thời với 2(t0) = 0,000 78 tính được
l2(t1) = ![]() = 0, 000 84 .
= 0, 000 84 .
Từ đó có 100t1l2(t1) = 100 x 850 x 0,000 84 = 37,4.
– Theo Bảng 3, giá trị gần với 37,4 nhất tương ứng với b = 2 có ba phương án trong Bảng A.1.
Bảng A.1
| n | 100t1l2(t1) | AQL* |
| 13 32 125 | 35 35 35 | 1,0 % 2,5 % 6,5 % |
Để chọn phương án kiểm tra thuận lợi nhất, cần phải xác định cường độ hư hỏng chấp nhận l1(t0) của một trong ba phương án trong Bảng A.1 với t0 = 1 500 h tương ứng với mỗi giá trị AQL* ở Bảng A.1. Tính được
| l1(t1) = | Giá trị 100t1l1(t1) từ Bảng 2 |
| 100 x 850 |
Trên cơ sở ![]() = 1, 75 tính được l1(t0) = 1,75 x l1(t1).
= 1, 75 tính được l1(t0) = 1,75 x l1(t1).
Kết quả trình bày ở Bảng A.2
Bảng A.2
| n | AQL* | 100t1l2(t1) | l1(t1) | l1(t0) |
| 13 32 125 | 1,0 % 2,5 % 6,5 % | 2,01 % 5,06 % 13,4 % | 0,000 023 6 0,000 059 5 0,000 157 6 | 0,000 041 3 0,000 104 1 0,000 275 8 |
Giả sử phương án thuận lợi nhất là trường hợp n = 32 và l1(t0) = 0,000 104 1 khi đó theo Bảng 1 với AQL* = 2,5 % và n = 32 có Ac = 2.
Kết luận: Từ lô cần kiểm tra, lấy ngẫu nhiên n = 32 sản phẩm đưa thử nghiệm trong khoảng thời gian t1 = 850 h. Xác định số sản phẩm hỏng r. Lô được chấp nhận nếu r ≤ 2 và bị bác bỏ nếu r ≥ 3.
Xác định các đại lượng phụ:
– Theo Bảng 1, với n = 32 giá trị N sẽ nằm trong khoảng từ 151 đến 280.
– Trên cơ sở l1(t0) = 0,000 104 1 và t0 = 1 500 h tính được
100t0l1(t0) = 15,61
– Theo Bảng 2, giá trị gần với 15,61 nhất là 13,4 tương ứng với b = 2 và AQL = 6,5 %.
– Theo Bảng 3, với n = 32 và AQL = 6,5 % tìm được LQ = 27,1 %.
MỤC LỤC
Lời nói đầu
1. Phạm vi áp dụng
2. Thuật ngữ, định nghĩa và ký hiệu
3. Quy định chung
4. Các phương án kiểm tra
Phụ lục A (tham khảo) Các ví dụ

