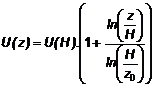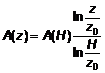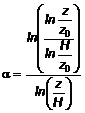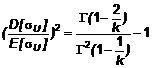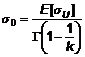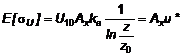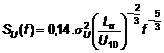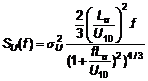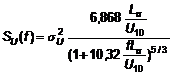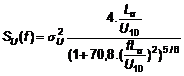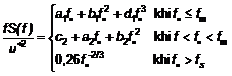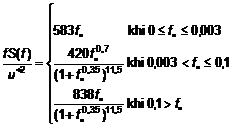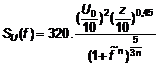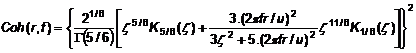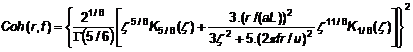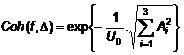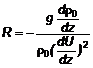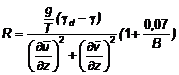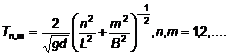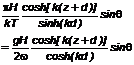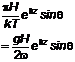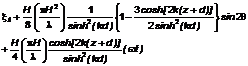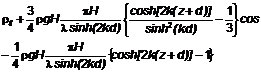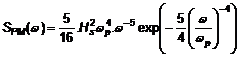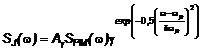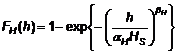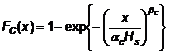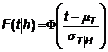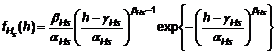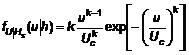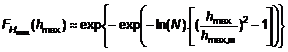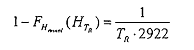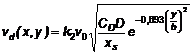GIÀN CỐ ĐỊNH TRÊN BIỂN - PHẦN 2: ĐIỀU KIỆN VÀ TẢI TRỌNG MÔI TRƯỜNG
Fixed offshore platforms - Part 2: Environmental conditions and environmental loads
Lời nói đầu
TCVN 6170-2: 2017 thay thế TCVN 6170-2: 1996.
TCVN 6170-2: 2017 do Cục Đăng kiểm Việt Nam biên soạn, Bộ Giao thông vận tải đề nghị, Tổng cục Tiêu chuẩn Đo lường Chất lượng thẩm định, Bộ Khoa học và Công nghệ công bố.
Bộ TCVN 6170 gồm 12 phần:
TCVN 6170-1: 2017 Giàn cố định trên biển - Phần 1: Quy định chung;
TCVN 6170-2: 2017 Giàn cố định trên biển - Phần 2: Điều kiện và tải trọng môi trường;
TCVN 6170-3: 2017 Giàn cố định trên biển - Phần 3: Tải trọng thiết kế;
TCVN 6170-4: 2017 Giàn cố định trên biển - Phần 4: Thiết kế kết cấu thép;
TCVN 6170-5: 1999 Công trình biển cố định - Kết cấu - Phần 5: Thiết kế kết cấu hợp kim nhôm;
TCVN 6170-6: 1999 Công trình biển cố định - Kết cấu - Phần 6: Thiết kế kết cấu bê tông cốt thép;
TCVN 6170-7: 1999 Công trình biển di động - Kết cấu - Phần 7: Thiết kế móng;
TCVN 6170-8: 1999 Công trình biển cố định - Kết cấu - Phần 8: Hệ thống chống ăn mòn;
TCVN 6170-9: 2000 Công trình biển cố định - Phần 9: Kết cấu - Giàn thép kiểu jacket;
TCVN 6170-10: 2000 Công trình biển cố định - Phần 10: Kết cấu - Giàn trọng lực bê tông;
TCVN 6170-11: 2002 Công trình biển cố định - Kết cấu - Phần 11: Chế tạo;
TCVN 6170-12: 2002 Công trình biển cố định - Kết cấu - Phần 12: Vận chuyển và lắp dựng.
GIÀN CỐ ĐỊNH TRÊN BIỂN - PHẦN 2: ĐIỀU KIỆN VÀ TẢI TRỌNG MÔI TRƯỜNG
Fixed offshore platforms - Part 2: Environmental conditions and environmental loads
Tiêu chuẩn này quy định các yêu cầu chung cho việc mô hình hóa, phân tích và dự báo điều kiện môi trường cũng như tính toán các tải trọng môi trường gây ra do gió, sóng và dòng chảy tác động lên giàn cố định trên biển (sau đây gọi tắt là giàn).
Tiêu chuẩn này đưa ra các tiêu chuẩn thiết kế hợp lý và đánh giá các tải trọng lên kết cấu giàn cố định trên biển chịu tác động của gió, sóng và dòng chảy.
Tiêu chuẩn này là cơ sở kỹ thuật áp dụng cho các giai đoạn: thiết kế, lắp đặt giàn cố định trên biển.
Các tài liệu viện dẫn sau rất cần thiết cho việc áp dụng Tiêu chuẩn này. Đối với các tài liệu viện dẫn ghi năm công bố thì áp dụng phiên bản được nêu. Đối với các tài liệu viện dẫn không ghi năm công bố thì áp dụng phiên bản mới nhất, bao gồm cả các sửa đổi, bổ sung (nếu có).
TCVN 6170-1:2017 Giàn cố định trên biển - Phần 1: Quy định chung
TCVN 6170-3:2017 Giàn cố định trên biển - Phần 3: Tải trọng thiết kế
TCVN 6170-4:2017 Giàn cố định trên biển - Phần 4: Thiết kế kết cấu thép
Recommended Practice DNV-RP-C205 Environmental Conditions and Environmental Loads
| ALS | Trạng thái giới hạn sự cố (Accidental Limit State) |
| BEM | Phương pháp phần tử biên (Boundary Element Method) |
| CF | Dòng vuông góc (Cross Flow) |
| CFD | Động lực học chất lỏng tính toán (Computational Fluid Dynamics) |
| CMA | Phương pháp mô hình hóa theo điều kiện (Conditional Modelling Approach) |
| COG | Trọng tâm (Center of Gravity) |
| CQC | Tổ hợp phương trình bậc 2 (Complete Quadratic Combination) |
| DVM | Phương pháp dòng rối rời rạc (Discrete Vortex Method) |
| EOF | Hàm trực giao thực nghiệm (Empirical Orthogonal Functions) |
| FD | Sai phân/vi phân hữu hạn (Finite Difference) |
| FEM | Phương pháp phần tử hữu hạn (Finite Element Method) |
| FLS | Trạng thái giới hạn mỏi (Fatigue Limit State) |
| FPSO | Kho chứa nổi (Floating Production and storage and Offloading) |
| FV | Thể tích hữu hạn (Finite Volume) |
| GBS | Kết cấu dựa trọng lực (Gravity Based Structure) |
| HAT | Triều thiên văn cao nhất (Highest Astronomical Tide) |
| HF | Tần số cao (High Frequency) |
| IL | Hướng dòng (In Line) |
| LAT | Triều thiên văn thấp nhất (Lowest Astronomical Tide) |
| LF | Tần số thấp (Low Frequency) |
| LNG | Khí tự nhiên hóa lỏng (Liquefied Natural Gas) |
| LS | Bình phương nhỏ nhất (Least Squares) |
| LTF | Hàm truyền tuyến tính (Linear Transfer Function) |
| MHWN | Triều rút cao trung bình (Mean High Water Neaps) |
| MHWS | Triều cường cao trung bình (Mean High Water Springs) |
| MLE | Đánh giá khả năng xảy ra lớn nhất (Maximum Likelihood Estimation) |
| MLM | Mô hình khả năng xảy ra lớn nhất (Maximum Likelihood Model) |
| MLWN | Triều rút thấp trung bình (Mean Low Water Neaps) |
| MLWS | Triều cường thấp trung bình (Mean Low Water Springs) |
| MOM | Phương pháp moment (Method of Moments) |
| PM | Pierson-Moskowitz |
| POT | Giới hạn đỉnh (Peak Over Threshold) |
| QTF | Hàm truyền bậc hai (Quadratic Transfer Function) |
| RAO | Toán tử biên độ phản ứng (Response Amplitude Operator) |
| SRSS | Căn bậc hai của tổng bình phương (Square Root of Sum of Squares) |
| SWL | Mực nước tĩnh (Still Water Level) |
| TLP | Giàn chân căng (Tension Leg Platform) |
| ULS | Trạng thái giới hạn cực hạn (Ultimate Limit State) |
| VIM | Chuyển động gây ra do dòng xoáy (Vortex Induced Motion) |
| VIO | Dao động gây ra do dòng xoáy (Vortex Induced Oscillations) |
| VIV | Dao động gây ra do dòng xoáy (Vortex Induced Vibrations) |
| VOF | Thể tích chất lỏng (Volume of Fluid) |
| WF | Tần số sóng (Wave Frequency) |
4.1 Điều kiện môi trường.
4.1.1 Điều kiện môi trường bao gồm các hiện tượng tự nhiên, làm ảnh hưởng đến độ bền, độ ổn định của công trình hoặc ảnh hưởng đến các hoạt động hàng hải. Tiêu chuẩn này quy định phương pháp xác định các hiện tượng chủ yếu tác động lên giàn là:
- Gió
- Sóng
- Dòng chảy
- Triều
4.1.2 Tiêu chuẩn này không đề cập đến một số hiện tượng môi trường khác do mỗi hiện tượng chỉ gây ra tác động rõ rệt tùy thuộc vào loại hình kết cấu và điều kiện khai thác cụ thể, bao gồm:
- Băng
- Động đất
- Điều kiện nền đất
- Nhiệt độ
- Hà biển
- Tầm nhìn
4.1.3 Hiện tượng môi trường thường được thể hiện theo các số liệu thống kê. Các số liệu này chỉ ra các điều kiện cực hạn cũng như trong quá trình thay đổi dài hay ngắn hạn. Nếu có được dãy số liệu đủ tin cậy, các hiện tượng tự nhiên có thể được mô tả bằng phương pháp xác suất chung (Joint probability).
4.1.4 Dữ liệu thiết kế môi trường được thu thập hoặc tham chiếu theo khu vực địa lý nơi công trình được lắp đặt hoặc nơi có hoạt động khai thác.
4.1.5 Dữ liệu thiết kế được sử dụng làm một cơ sở cho thiết kế và đánh giá hoạt động phải lấy trong một khoảng thời gian đủ dài. Đối với những giàn hoạt động trong một thời gian hạn chế, sự thay đổi theo mùa phải đưa vào trong tính toán. Các dữ liệu khí tượng và hải dương được ghi lại trong 20 năm phải có sẵn. Nếu dữ liệu được ghi lại trong khoảng thời gian ngắn không đảm bảo, dữ liệu đó phải được đưa vào phân tích.
4.2 Tải trọng môi trường
Tải trọng môi trường là tải trọng do các hiện tượng môi trường gây ra.
Tải trọng môi trường sử dụng cho thiết kế phải dựa trên các dữ liệu môi trường tại các vị trí xây dựng cụ thể và phạm vi nơi có hoạt động diễn ra. Tải trọng này được xác định bằng việc sử dụng các lý thuyết tương đương áp dụng cho từng hiện tượng môi trường, từng loại, kích cỡ, hình dạng công trình và các phản ứng đặc trưng xảy ra trong quá trình chịu tải trọng.
5.1.1 Tổng quát
Tốc độ gió thay đổi theo thời gian và chiều cao trên mặt đất hoặc trên mặt nước biển. Vì thế, thời gian trung bình và chiều cao tham chiếu phải được xác định.
Chiều cao tham chiếu H = 10 m trên mực nước biển thường được sử dụng. Thời gian trung bình thường lấy theo 1 phút, 10 phút và 1 giờ. Vận tốc gió trung bình trong 1 phút thường được đưa vào trong tính toán thiết kế (được xem như là tốc độ gió duy trì).
5.1.2 Các thông số gió
5.1.2.1 Gió được xác định bởi tốc độ gió trung bình trong 10 phút (U10) và độ lệch chuẩn (σU) tại độ cao 10 m. Trong điều kiện ngắn hạn, khoảng trên 10 phút, các điều kiện gió với U10 và σU thường được giả định là không đổi và chủ đạo. Các điều kiện gió này không bao gồm các hiện tượng xảy ra trong bão nhiệt đới như bão, lốc xoáy, cũng không bao gồm các hiện tượng xảy ra trong các trường hợp có quy mô nhỏ. Dữ kiện/giả thiết trong các điều kiện gió tĩnh trên 10 phút thường không có giá trị. Ví dụ, sự chuyển trạng thái gió ban đầu không ổn định có thể gây ra các điều kiện cực hạn như sự tăng tốc độ và hướng thay đổi đột ngột (gió giật).
5.1.2.2 Tốc độ gió trung bình trong 10 phút (U10) là một đại lượng cường độ gió. Độ lệch chuẩn (σU) là một đại lượng thể hiện sự thay đổi tốc độ gió. Khi xảy ra các hiện tượng đặc biệt, như bão, lốc, các giá trị U10 và σU là chưa đủ. Tốc độ gió tức thời tại một điểm bất kỳ xảy ra trong khoảng thời gian 10 phút là một phân phối xác suất với giá trị trung bình U10 và độ lệch chuẩn σU.
5.1.2.3 Cường độ rối được xác định bởi tỷ số σU/U10.
5.1.2.4 Gió trong trạng thái ngắn hạn 10 phút thường được mô tả bằng một phổ gió, nghĩa là mật độ năng lượng phổ của vận tốc gió SU(f) - là hàm của U10 và σU, thể hiện năng lượng của vận tốc gió tại một điểm cụ thể trong không gian theo các khoảng tần số khác nhau.
5.2.1 Thống kê tốc độ gió
5.2.1.1 Các thống kê tốc độ gió được phân loại theo các điều kiện gió ngắn và dài hạn. Điều kiện gió dài hạn thường được lấy theo các dữ liệu ghi lại trong 10 năm hoặc hơn. Điều kiện gió ngắn hạn trong 10 phút. Vận tốc gió trung bình 10 phút tại độ cao 10 m trên mặt đất hoặc mực nước biển trung bình được sử dụng như một thông số cơ bản mô tả sự dao động của vận tốc gió dài và ngắn hạn. Số liệu thống kê thực nghiệm được sử dụng làm cơ sở thiết kế phải được lấy trong một khoảng thời gian đủ dài.
5.2.1.2 Số liệu gió đo tại khu vực cụ thể phải được thực hiện một khoảng thời gian liên tục đủ dài hoặc ít có sự gián đoạn. Trong thiết kế, cơ sở dữ liệu gió phải trong thời gian 10 năm hoặc các dữ liệu liên tục có đủ thời gian phân tích.
5.2.1.3 Tốc độ gió phụ thuộc vào độ cao. Tốc độ gió trung bình tại độ cao 10 m được sử dụng để tham chiếu. Khi không có sẵn các dữ liệu tốc độ gió, tốc độ gió tại những độ cao khác nhau có thể được tính toán từ tốc độ gió tại độ cao tham chiếu kết hợp với profile tốc độ gió trên mặt đất hoặc trên mực nước biển trung bình.
5.2.1.4 Sự phân phối dài hạn của U10 và σU phải dựa theo số liệu thống kê tương tự từ chu kỳ trung bình của tốc độ gió để xác định các tải trọng. Nếu một chu kỳ trung bình khác 10 phút được sử dụng để xác định tải trọng, dữ liệu gió có thể được xác định bằng cách áp dụng hệ số gió giật thích hợp. Phân phối ngắn hạn của tốc độ gió tức thời phụ thuộc vào U10 và σU.
5.2.1.5 Hệ số gió giật thích hợp để chuyển đổi các số liệu gió từ các khoảng chu kỳ trung bình khác nhau hơn 10 phút phụ thuộc vào vị trí tần suất của một khoảng phổ. Nếu áp dụng của một hệ số gió giật cố định độc lập với vị trí tần suất của một khoảng phổ có thể dẫn tới kết quả không chính xác. Một khoảng phổ tách các chuyển động có quy mô lớn từ các chuyển động rối loạn và tham chiếu theo không gian và tỷ lệ tạm thời để chỉ ra những sự thay đổi nhỏ trong tốc độ gió.
5.2.1.6 Kết quả profile gió trên mặt nước biển phải được xác định cho các trường hợp thay đổi về độ cao, tốc độ gió trong các khoảng thời gian trung bình khác nhau.
5.2.1.7 Vận tốc gió tại vị trí tính toán phải dựa trên số liệu đo đạc tại vị trí thực tế và các vị trí liền kề, các dữ liệu được thu thập trước đây cũng như những mô hình lý thuyết và các thông tin khí tượng học khác. Nếu các dữ liệu vận tốc gió không đủ và không đảm bảo, việc đo vận tốc gió phải được tiến hành tại vị trí yêu cầu để xác định các giá trị đặc trưng của vận tốc gió.
5.2.1.8 Các mô hình thiết lập dữ liệu gió và các mô hình lý thuyết có thể được chấp nhận bằng kết quả so sánh với dữ liệu đo được.
5.3.1 Tốc độ gió trung bình
5.3.1.1 Phân phối xác suất dài hạn của các thông số gió U10 và σU được lấy từ dữ liệu có sẵn thường mô tả theo các phân phối chung hoặc các biểu đồ phân tán. Phân phối chung bao gồm một phân phối Weibull cho vận tốc gió trung bình 10 phút U10 kết hợp với một phân phối lô-ga-rit chuẩn σU theo điều kiện U10. Biểu đồ phân tán đưa ra tần số xuất hiện của các cặp số rời rạc (U10, σU) trong khoảng không gian chứa các đại lượng (U10, σU).
5.3.1.2 Trường hợp dữ liệu không có những đột biến, phân phối Weibull có thể được xác định vận tốc gió trung bình U10 tại độ cao z bất kỳ trên mặt đất hoặc trên mực nước biển trung bình.
|
| (1) |
Trong đó tham số tỷ lệ A và tham số hình dạng k phụ thuộc vào vị trí và chiều cao.
5.3.1.3 Trong khu vực có bão, phân phối Weibull được xác định theo tốc độ gió 10 phút là không chính xác đối với phần đồ thị đỉnh trên của phân phối thực U10 (the upper tail of true distribution of U10). Do đó, trong các khu vực như vậy, phần đồ thị đỉnh trên của phân phối thực U10 phải được xác định trên cơ sở dữ liệu bão.
5.3.1.4 Dữ liệu cho U10 thường thu được bằng việc đo và tính tốc độ trung bình gió trong 10 phút. Có nhiều phương án lấy mẫu trong đó U10 được quan trắc từ mỗi khoảng 10 phút liên tiếp (6 lần quan trắc mỗi giờ) hoặc U10 được quan trắc 10 phút mỗi giờ hoặc 3 giờ 1 lần (24 hoặc 8 lần quan sát U10 mỗi ngày).
5.3.1.5 Bất kể giá trị U10 được lấy trong chu kỳ 10 phút, một giờ hoặc 3 giờ, các mẫu quan trắc được lấy trong vài năm sẽ tạo thành một tập hợp dữ liệu giá trị U10 ![]() theo U10.
theo U10.
5.3.1.6 Tại vị trí không có bão, phân phối của vận tốc gió trung bình hàng năm 10 phút lớn nhất được tính gần đúng bởi công thức:
|
| (2) |
Trong đó: N = 52560 là số lần các khoảng trung bình 10 phút liên tục trong một năm, với năm nhuận N = 52595. Công thức gần đúng này dựa trên một giả thuyết độc lập trong 10 phút, là một phép xấp xỉ đảm bảo cho phần đồ thị đỉnh trên của phân phối, thường sử dụng để dự đoán tốc độ gió trung bình ít xảy ra với chu kỳ lặp 50 và 100 năm.
5.3.1.7 Giá trị N = 52560 được xác định dựa trên cơ sở chu kỳ trung bình 10 phút được chọn và không bị ảnh hưởng bởi quy trình lấy mẫu để lập ra dữ liệu cho vận tốc gió U10 và phân phối ![]() ; tức là không phụ thuộc vào vận tốc trung bình trong 10 phút U10 được lấy trong mỗi 10 phút, 1 giờ hay mỗi 1/3 giờ. Giá trị cực đại ước lượng đến 99% khả năng trong kết quả phân phối của tốc độ gió trung bình 10 phút hàng năm sẽ thường đưa ra độc lập với tần số lấy mẫu.
; tức là không phụ thuộc vào vận tốc trung bình trong 10 phút U10 được lấy trong mỗi 10 phút, 1 giờ hay mỗi 1/3 giờ. Giá trị cực đại ước lượng đến 99% khả năng trong kết quả phân phối của tốc độ gió trung bình 10 phút hàng năm sẽ thường đưa ra độc lập với tần số lấy mẫu.
5.3.1.8 Tại nơi có bão xảy ra, sự phân phối tốc độ gió trung bình 10 phút hàng năm U10 phải được dựa trên dữ liệu bão có sẵn.
5.3.1.9 Phép xấp xỉ lũy thừa với phân phối của tốc độ gió trung bình 10 phút hàng năm lớn nhất là một phép xấp xỉ tin cậy cho phần đồ thị đỉnh trên của phân phối. Thông thường chỉ các điểm phân vị của phần đồ thị đỉnh trên của phân phối được quan tâm, tức là 98% phân vị xác định tốc độ gió trung bình 50 năm hoặc 99% phân vị xác định tốc độ gió trung bình 100 năm. Phần đồ thị đỉnh trên của phân phối có thể lấy xấp xỉ bằng phân phối Gumbel mà công thức của nó có tính sử dụng nhiều hơn là công thức luật lũy thừa.
5.3.1.10 Tốc độ gió trung bình trong 10 phút lớn nhất hàng năm thường được giả định theo 1 phân phối Gumbel:
|
| (3) |
Trong đó a và b là thông số phân phối phụ thuộc vào vị trí và độ cao.
5.3.1.11 Kinh nghiệm chỉ ra trong nhiều trường hợp, phân phối Gumbel đưa ra một đại diện cho phân phối của bình phương tốc độ gió trung bình trong 10 phút lớn nhất hàng năm tốt hơn của phân phối vận tốc gió trung bình lớn nhất hàng năm. Tải trọng gió gây ra do áp lực gió, tương ứng với bình phương tốc độ gió, vì thế để đánh giá tải trọng đặc trưng xác định bởi 98% hoặc 99% phân vị trong phân phối của tải trọng gió lớn nhất hàng năm, cần được yêu cầu tính toán với phân phối của bình phương tốc độ gió trung bình 10 phút hàng năm lớn nhất và ngoại suy đến giá trị 50 hoặc 100 năm của phân phối.
5.3.1.12 Tốc độ gió trung bình trong 10 phút với chu kỳ lặp một năm TR được định nghĩa là ![]() phân vị trong phân phối của tốc độ gió trung bình 10 phút hàng năm lớn nhất, tức là xác suất vượt trong một năm của tốc độ gió trung bình 10 phút là
phân vị trong phân phối của tốc độ gió trung bình 10 phút hàng năm lớn nhất, tức là xác suất vượt trong một năm của tốc độ gió trung bình 10 phút là ![]() . Được kí hiệu là
. Được kí hiệu là ![]() và được biểu diễn bằng:
và được biểu diễn bằng:
|
| (4) |
Trong đó ![]() thể hiện hàm phân phối tích lũy của tốc độ gió trung bình 10 phút hàng năm lớn nhất.
thể hiện hàm phân phối tích lũy của tốc độ gió trung bình 10 phút hàng năm lớn nhất.
5.3.1.13 Tốc độ gió trung bình trong 10 phút với chu kỳ lặp 1 năm được định nghĩa là cách thức phân phối của tốc độ gió trung bình 10 phút lớn nhất hàng năm.
5.3.1.14 Tốc độ gió trung bình 10 phút trong 50 năm:
|
| (5) |
Tốc độ gió trung bình 10 phút trong 100 năm:
|
| (6) |
Các giá trị được tính toán theo công thức trên phải được xác định như ước lượng trung bình của tốc độ gió tương ứng 10 phút khi hàm phân phối cơ bản FU10,max được xác định từ dữ liệu giới hạn và bị hạn chế với thống kê không rõ ràng.
5.3.2 Profile tốc độ gió
5.3.2.1 Profile tốc độ gió thể hiện sự thay đổi của tốc độ gió trung bình với chiều cao trên mặt đất hoặc trên mặt nước tĩnh. Khi điều kiện địa hình và điều kiện ổn định khí áp không phức tạp, profile tốc độ gió có thể được đại diện bởi 1 mô hình lý tưởng. Các mô hình gió được áp dụng hầu hết là các mô hình lô-ga-rit, mô hình lũy thừa và mô hình Frøya.
5.3.2.2 Những profile gió phức tạp do sự đảo ngược hoặc không được miêu tả bởi các mô hình gió được áp dụng, có thể chiếm ưu thế trong vùng lân cận nước biển
5.3.2.3 Vận tốc ma sát u* được định nghĩa:
|
| (7) |
Trong đó t là ứng suất cắt trên mặt phẳng và ρa là mật độ không khí.
Vận tốc ma sát u* có thể được tính toán từ tốc độ gió trung bình trong 10 phút U10 tại độ cao H = 10 m như sau:
|
| (8) |
Trong đó κ là hệ số ma sát mặt phẳng. Một số nguồn tham khảo xem κ là hệ số cản mặt phẳng; tuy nhiên, hệ số κ không được nhầm với hệ số cản sử dụng trong việc tính toán lực gió lên công trình.
5.3.2.4 Profile tốc độ gió lô-ga-rit được giả định cho điều kiện khí áp trung lập và được thể hiện bằng công thức:
|
| (9) |
Trong đó ka = 0,4 là hằng số von Karman, z là độ cao và z0 là hệ số nhám của địa hình. Với những vị trí trên đất liền, z0 phụ thuộc vào địa hình và vị trí tự nhiên. Với những vị trí ngoài khơi z0 phụ thuộc tốc độ gió, khoảng cách ngược với đất liền, độ sâu nước và trường sóng. Bảng 1 đưa ra những giá trị đặc trưng của hệ số nhám cho nhiều loại địa hình khác nhau.
Bảng 1 - Hệ số nhám z0 và số mũ α
| Loại địa hình | Hệ số nhám z0 (m) | Số mũ α |
| Băng | 0,00001 đến 0,0001 |
|
| Biển mở không sóng | 0,0001 |
|
| Biển mở có sóng | 0,0001 đến 0,01 | 0,12 |
| Bờ biển với gió trên đất liền | 0,001 đến 0,01 |
|
| Tuyết | 0,001 đến 0,006 |
|
| Vùng ngoại ô không có nhà và cây cối cao đáng kể | 0,01 |
|
| Bãi cỏ | 0,01 |
|
| Khu đất trống | 0,02 đến 0,03 |
|
| Cỏ dài, đá xung quanh | 0,05 |
|
| Đất trồng có những công trình rời rạc | 0,05 | 0,16 |
| Đất trồng trọt | 0,2 |
|
| Rừng và khu ngoại ô | 0,3 | 0,30 |
| Trung tâm thành phố | 1 đến 10 | 0,40 |
5.3.2.5 Tại các vị trí ngoài khơi, hệ số nhám z0 thường thay đổi từ 0,0001 m trong vùng biển mở không sóng đến 0,01 m tại khu vực bờ biển có gió trên bờ. Hệ số nhám cho khu vực ngoài khơi có thể lý giải hoàn toàn từ công thức dưới đây:
|
| (10) |
Trong đó g là gia tốc trọng trường và AC là hằng số Charnock. AC thường cao hơn đối với các sóng trẻ và phát triển nhanh hơn so với các sóng đã phát triển. Đối với vùng biển mở có sóng đã phát triển hoàn toàn, AC =0,011 đến 0,014. Với vị trí gần bờ, AC thường lấy lớn hơn 0,018.
5.3.2.6 Công thức thay thế cho profile lô-ga-rit, biểu diễn theo tốc độ gió trung bình trong 10 phút U (H) tại độ cao tham chiếu H =10 m:
|
| (11) |
Trong đó:
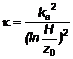 là hệ số ma sát mặt phẳng.
là hệ số ma sát mặt phẳng.
Do đó Profile lô-ga-rit được viết lại dưới dạng:
|
| (12) |
5.3.2.7 Profile tốc độ gió lô-ga-rit chỉ ra rằng thông số A(z) tại độ cao z có thể biểu diễn dưới dạng thông số A(H) tại độ cao H như sau:
|
| (13) |
5.3.2.8 Profile lũy thừa thay thế cho profile gió lô-ga-rit:
|
| (14) |
Trong đó số mũ α phụ thuộc vào độ nhám của bề mặt.
5.3.2.9 Nếu phương trình lô-ga-rit và luật lũy thừa được kết hợp, công thức phụ thuộc vào cao độ cho kết quả của số mũ α:
|
| (15) |
5.3.2.10 Cần chú ý rằng giá trị giới hạn α =1/ln(z/z0) khi z tiến gần đến chiều cao tham chiếu H. Để thay thế cho công thức tính α, giá trị α được cho trong Bảng 1 có thể được sử dụng.
5.3.2.11 Công thức sau có thể được sử dụng để tính toán tốc độ gió trung bình U trong khoảng thời gian trung bình T tại độ cao z trên mực nước biển:
|
| (16) |
Trong đó H = 10 m và T10 = 10 phút, U10 là tốc độ gió trung bình trong 10 phút tại độ cao H.
Công thức này chuyển đổi tốc độ gió trung bình giữa những khoảng thời gian khác nhau. Khi T < T10, công thức đưa ra tốc độ gió trung bình lớn nhất trên khoảng thời gian T xác định, cho chu kỳ trung bình 10 phút đầu tiên với các điều kiện tĩnh và tốc độ gió trung bình 10 phút U10.
5.3.2.12 Mô hình profile gió Frøya được khuyến nghị sử dụng đối với vị trí ngoài khơi. Với tốc độ gió trung bình cực hạn tương ứng với chu kỳ lặp vượt quá 50 năm, mô hình Frøya đưa ra công thức dưới đây để chuyển đổi tốc độ gió trung bình trong 1 giờ U0 tại độ cao H trên mặt biển sang tốc độ gió trung bình U trong khoảng thời gian trung bình T tại độ cao z trên mặt biển:
|
| (17) |
Trong đó H = 10 m, T0 = 1 giờ, với T < T0,
|
| (18) |
Trong đó tốc độ gió trung bình U có chu kỳ lặp tương tự U0.
5.3.2.13 Profile tốc độ gió gồm một hệ số gió giật cho phép chuyển tốc độ gió trung bình giữa những khoảng thời gian trung bình khác nhau. Profile tốc độ gió Frøya là một trường hợp đặc biệt của profile tốc độ gió lô-ga-rit và là profile tốt nhất cho điều kiện ngoài biển.
5.3.2.14 Tại vùng biển mở, hệ số C có xu hướng nhỏ hơn khoảng 10% kết quả từ công thức nêu trên. Tại vị trí bờ, giá trị hệ số C được sử dụng cao hơn, 15% với U0 = 10 m/s và hơn 30% với U0 = 40 m/s.
5.3.2.15 Cả hai công thức chuyển đổi được dựa trên dữ liệu bão mùa đông của vùng biển Nauy và có thể không thích hợp tại các vị tri khác. Các công thức đó không nên được ngoại suy để sử dụng ngoài phạm vi độ cao được xác định, tức là không nên sử dụng cho chiều cao trên 100 m. Ảnh hưởng xảy ra từ các địa hình gió xuống khoảng 100 m cao làm tăng tầm quan trọng vì sự hạn chế khi quan trắc.
5.3.2.16 Cả hai công thức chuyển đổi được dựa trên việc áp dụng một profile gió lô-ga-rit. Tại những vị trí có số mũ profile gió được sử dụng hoặc bắt buộc, hai công thức phải được xem xét chỉ sử dụng cho việc chuyển đổi những khoảng thời gian trung bình khác nhau tại một độ cao bằng độ cao tham chiếu H = 10 m.
5.3.2.17 Trong trường hợp thiếu thông tin về gió bão nhiệt đới trong khu vực quan tâm, các công thức chuyển đổi cũng có thể được áp dụng cho những cơn gió bắt nguồn từ bão nhiệt đới.
5.3.2.18 Các công thức chuyển đổi không phù hợp đối với gió giật mạnh, đặc biệt đối với khoảng thời gian gió giật ít hơn một giờ.
5.3.2.19 Khi một mô hình profile gió được chọn, điều quan trọng là sử dụng mô hình này một cách nhất quán, tức là mô hình profile gió được sử dụng để đổi tốc độ gió tại độ cao z sang tốc độ gió tại độ cao tham chiếu H phải được áp dụng cho mọi tính toán tiếp theo của tốc độ gió, tại cả chiều cao z và tại chiều cao khác, dựa theo tốc độ gió tại chiều cao tham chiếu H.
5.3.2.20 Các mô hình profile gió được sử dụng cho việc chuyển đổi tốc độ gió mà không có sự quan trắc là các mô hình đặc thù lý tưởng hóa được giả định cho các profile gió trung bình trong điều kiện ngắn hạn. Đó là mô hình có tính thay đổi kết hợp với profile và nhiều sự thay đổi xung quanh: profile trung bình thực có thể lấy một dạng khác từ vài sự kiện gió, như trong trường hợp gió cực đại hoặc trong điều kiện gió không chuẩn. Hệ quả chỉ ra việc chuyển đổi dữ liệu gió theo độ cao không dựa trên kết quả đo sẽ tồn tại sự không đảm bảo.
5.3.2.21 Các công thức nêu trong 5.3.2.11 và 5.3.2.12 gồm các thông số gió giật chuyển đổi tốc độ gió giữa những chu kỳ trung bình khác nhau. Việc chuyển đổi tốc độ gió giữa các chiều cao khác nhau cũng như việc chuyển đổi giữa các chu kỳ trung bình có sự không đảm bảo, như sự đơn giản trong các mô hình sử dụng việc chuyển đổi.
5.3.3 Mô hình rối của tải trọng gió
5.3.3.1 Sự thay đổi tự nhiên của tốc độ gió trung bình trong 10 phút U10 được coi là mô hình rối của tải trọng gió và được biểu thị bởi độ lệch chuẩn σU. Với giá trị U10 được cho độ lệch chuẩn σU của tốc độ gió chỉ ra sự thay đổi tự nhiên từ một khoảng thời gian 10 phút sang khoảng thời gian khác. Việc đo đạc từ nhiều vị trí chỉ ra giá trị σU theo điều kiện U10 có thể được biểu diễn bởi một phân phối lô-ga-rít chuẩn.
|
| (19) |
Trong đó: Ф( ) biểu thị hàm phân phối tích lũy chuẩn Gaussian:
![]()
Hệ số b0 và b1 là hệ số phụ thuộc vào U10.
5.3.3.2 Hệ số b0 có thể được giải thích như giá trị trung bình của lnσU, và b1, như độ lệch chuẩn của lnσU. Việc tính toán giá trị trung bình E[σU] và độ lệch chuẩn D[σU] của σU từ các giá trị b0 và b1:
|
| (20) |
|
| (21) |
5.3.3.3 E[σU] và D[σU] ngoài phụ thuộc vào U10, còn phụ thuộc vào các điều kiện cục bộ, độ nhám địa hình z0 hay chiều dài độ nhám. Khi độ nhám địa hình khác xuất hiện tại các nhiều hướng khác nhau, ví dụ tại địa hình không bằng phẳng, E[σU] và D[σU] có thể thay đổi theo hướng, ví dụ trong các vùng lân cận của một công trình lớn. Công trình và các phần tử gây nhiễu thường sẽ dẫn đến rối nhiều hơn, giá trị lớn hơn của E[σU] và D[σU] xảy ra tại địa hình phẳng hơn. Hình 1 và Hình 2 đưa ra các ví dụ của sự thay đổi của E[σU] và D[σU] cho U10 tại vị trí trên bờ và ngoài khơi. Sự khác nhau giữa hai đồ thị chủ yếu là hình dạng của đường cong trung bình. Điều này phản ánh ảnh hưởng của sự tăng chiều dài độ nhám khi tăng U10 tại ví trí ngoài khơi.

Hình 1 - Ví dụ về giá trị trung bình và độ lệch chuẩn σU theo U10 - Vị trí trên bờ
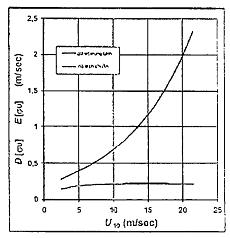
Hình 2 - Ví dụ về giá trị trung bình và độ lệch chuẩn σU theo U10 - Vị trí ngoài khơi
5.3.3.4 Trong một vài trường hợp, một phân phối lô-ga-rit chuẩn σU dựa trên điều kiện U10 sẽ đánh giá thấp giá trị cao hơn của σU. Một phân phối Frechet có thể tạo thành một mô hình phân phối hấp dẫn σU như sau:
|
| (22) |
Thông số phân phối k được giải thích gián tiếp từ công thức:
|
| (23) |
Và giá trị của σ0:
|
| (24) |
Trong đó Γ biểu thị hàm gamma:
|
| (25) |
5.3.3.5 Cần thận trọng khi điều chỉnh một mô hình phân phối với dữ liệu. Thông thường phân phối lô-ga-rit chuẩn đưa ra dữ liệu phù hợp, nhưng việc sử dụng một phân phối chuẩn, một phân phối Weibull hoặc một phân phối Frechet cũng cần được xem xét. Việc lựa chọn mô hình phân phối phụ thuộc vào việc áp dụng mô hình đó, tức là việc điều chỉnh với dữ liệu là yêu cầu với toàn bộ phân phối hoặc với phần thân hoặc phần đỉnh trên của đồ thị phân phối. Điều quan trọng là việc xác định và loại bỏ dữ liệu trong chuỗi thời gian 10 phút mà các dữ kiện U10 không đủ.
Nếu không, các dữ liệu có thể làm xáo trộn việc xác định mô hình phân phối thích hợp cho σU theo điều kiện U10.
5.3.3.6 Công thức dưới đây tính giá trị trung bình của độ lệch chuẩn σU, theo điều kiện U10 có thể được áp dụng đối với địa hình đồng nhất:
|
| (26) |
Trong đó:
ka là hằng số von Karman. (ka = 0,4)
z là độ cao trên mặt địa hình.
z0 là hệ số nhám.
Ax là hằng số phụ thuộc vào z0.
Việc đo đạc từ một số vị trí đồng đều và bằng phẳng chỉ ra giá trị trung bình của Ax bằng 2,4. Tại ví trị sườn dốc, Ax có xu hướng lớn hơn. Nếu dữ liệu không chỉ ra sự khác, công thức gần đúng Ax có thể được sử dụng cho dòng chảy rối cơ học trên địa hình đồng đều và bằng phẳng:
|
| (27) |
Trong đó z0 có đơn vị mét.
5.3.3.7 Tốc độ gió trung bình 10 phút U10 và độ lệch chuẩn của tốc độ gió σU đề cập đến tốc độ gió theo chiều dọc, tức là tốc độ gió theo hướng không đổi trong một khoảng thời gian 10 phút theo các điều kiện tĩnh. Trong khoảng thời gian này, ngoài những biến động theo hướng gió trung bình, cũng sẽ xảy ra sự rối theo chiều ngang và đứng. Tốc độ gió trung bình ngang sẽ bằng không, trong khi độ lệch chuẩn của tốc độ gió có thể lấy bằng giá trị trong khoảng 0,75σU và 0,80σU. Tốc độ gió trung bình đứng sẽ bằng không, trong khi độ lệch chuẩn đứng của tốc độ gió có thể lấy là σUz= 0,5 σU. Tất cả các giá trị được tham chiếu theo địa hình đồng nhất. Đối với địa hình phức tạp, vùng tốc độ gió sẽ là đẳng hướng nhiều hơn, và các giá trị của σUy và σUz rất gần với giá trị của mong muốn của σU.
5.3.3.8 Khi gió tại vị trí không được đo cụ thể, phân phối của U10 có thể vẫn được lấy trên cơ sở các phép đo tốc độ gió tại các vị trí liền kề. Tuy nhiên phân phối của σU thường khó thu được vì sự phụ thuộc vào điều kiện độ nhám cục bộ đặc biệt, và không cần thiết được suy ra từ điều kiện tốc độ gió đã biết tại các điểm liền kề. Tại một vị trí mà các phép đo tốc độ gió không có sẵn, việc xác định phân phối của độ lệch chuẩn tốc độ gió σU thường có sự không rõ ràng. Do đó σU thường được lấy cao hơn cho mục đích thiết kế.
5.3.4 Phổ gió
5.3.4.1 Các điều kiện gió tĩnh ngắn hạn có thể được miêu tả bằng một phổ gió, tức là mật độ phổ năng lượng của tốc độ gió. Các mật độ phổ tại vị trí xác định của tốc độ gió có thể được xác định từ dữ liệu đo đạc có sẵn.
5.3.4.2 Khi các mật độ phổ dựa trên dữ liệu đo đạc được sử dụng, độ tích tụ năng lượng trong dải tần số cao phải được thỏa mãn, mặt khác nếu dữ liệu không chỉ ra sự khác nhau: mật độ phổ SU(f) sẽ tiệm cận dạng dưới đây khi tần số f nằm trong dải tần số cao tăng lên:
|
| (28) |
Trong đó Lu là đà gió (integral length scale) của quá trình tốc độ gió.
5.3.4.3 Mặt khác nếu dữ liệu không chỉ ra sự khác nhau, mật độ phổ của quá trình tốc độ gió có thể được đại diện bằng một phổ mô hình. Một số phổ mô hình tồn tại, chấp nhận dải tần số cao, trong khi một số phổ lớn khác tồn tại trong dải tần số thấp. Hầu hết phổ mô hình có sẵn được điều chỉnh với dữ liệu gió thu được trên mặt đất. Một số ít được điều chỉnh với dữ liệu thu được trên mặt nước. Phổ mô hình thường được biểu diễn theo quy mô chiều dài của quá trình tốc độ gió. Việc phổ biến nhất được sử dụng phổ mô hình với đà gió trong phổ gió được trình bày trong 5.3.4.5 đến 5.3.4.10.
5.3.4.4 Mô hình phổ phải được nghiên cứu khi sử dụng. Trong đó, điều quan trọng là đà gió có thể chênh đáng kể với đà gió của phổ mô hình.
5.3.4.5 Phổ Davenport thể hiện mật độ phổ theo tốc độ gió trung bình 10 phút U10 không phụ thuộc vào độ cao. Phổ Davenport đưa ra công thức dưới đây cho mật độ phổ:
|
| (29) |
Trong đó f biểu thị tần số và Lu là đà gió. Phổ Davenport được phát triển ban đầu cho gió trên mặt đất với giá trị đề xuất Lu = 1200 m.
5.3.4.6 Phổ Davenport không được khuyến nghị để sử dụng trong dải tần số thấp, f < 0,01 Hz. Vì sự giảm mạnh giá trị mật độ phổ của phổ Davenport gần với tần số 0, nên có sự khó khăn trong việc kết hợp phổ Davenport với dữ liệu trong dải tần số này.
5.3.4.7 Phổ Kaimal đưa ra công thức dưới đây cho mật độ phổ:
|
| (30) |
trong đó f biểu thị tần số và Lu là đà gió. Nếu dữ liệu không chỉ ra sự khác biệt, đà gió Lu có thể được tính bằng:
|
| (31) |
trong đó z biểu thị cho độ cao trên mật đất hoặc mực nước biển, z0 là độ nhám bề mặt. Cả z và z0 có đơn vị mét.
5.3.4.8 Đà gió cho việc thiết kế máy phát điện tua bin gió và không phụ thuộc vào độ nhám bề mặt:
|
| (32) |
Trong đó z đại diện cho chiều cao trên mặt đất hoặc mực nước biển.
5.3.4.9 Phổ Harris thể hiện mật độ phổ với tốc độ gió trung bình 10 phút U10 không phân biệt độ cao. Phổ Harris đưa ra công thức dưới đây cho mật độ phổ:
|
| (33) |
Trong đó là Lu là đà gió, nằm trong khoảng 60 - 400 m với giá trị trung bình là 180 m. Nếu dữ liệu không chỉ ra sự khác biệt, đà gió Lu có thể được tính toán như với phổ Kaimal, xem 5.3.4.6. Phổ Harris được phát triển ban đầu cho gió trên mặt đất và không khuyến khích sử dụng trong dải tần số thấp f < 0,01 Hz.
5.3.4.10 Trong thiết kế kết cấu giàn, Phổ thực nghiệm Simiu và Leigh có thể được áp dụng. Phổ mô hình này được phát triển để đưa vào tính toán năng lượng gió trên mặt biển trong dải tần số thấp. Phổ Simiu và Leigh S(f) thu được từ công thức dưới đây:
|
| (34) |
Trong đó:
![]()
f là tần số.
z là độ cao trên mực nước biển tĩnh.
U10 là tốc độ gió trung bình 10 phút tại độ cao z.
![]()
![]()
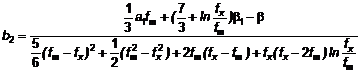
![]()
![]()
![]()
![]()
![]()
fm là tần số không thứ nguyên khi fS(f) lớn nhất.
fs là tần số không thứ nguyên tương đương với giới hạn dưới của vùng con quán tính (inertial subrange).
Độ lớn của đà gió Lu thường nằm trong khoảng từ 100 m đến 240 m với gió tại độ cao 20 m đến 60 m trên mặt biển. Nếu dữ liệu không chỉ ra sự khác biệt, Lu có thể được tính toán theo phổ Kaimal, xem 5.3.4.7.
5.3.4.11 Đối với thiết kế kết cấu giàn, phổ thực nghiệm Ochi và Shin có thể được áp dụng. Mô hình này được phát triển từ phổ đã được đo trên một đường biển. Phổ Ochi và Shin S(f) có thể được áp dụng từ các công thức sau:
|
| (35) |
Trong đó:
![]()
Phổ Ochi và Shin có nhiều năng lượng trong dải tần số thấp (f < 0,01 Hz) hơn các mô hình phổ truyền thống sử dụng đại diện gió trên mặt đất là Davenport, Kaimal và Harris.
Tuy nhiên với các tần số ít hơn khoảng 0,001 Hz, phổ Ochi và Shin có ít năng lượng hơn mô hình phổ thay thế Frøya với gió trên mặt biển. Đó là một dải tần số mà phổ Ochi và Shin không được điều chỉnh với dữ liệu đo đạc trừ một chức năng đơn giản lý tưởng.
5.3.4.12 Đối với các trường hợp kích thích trong dải tần số thấp là đáng kể, mật độ phổ mô hình Frøya được khuyến nghị cho gió trên mặt nước:
|
| (36) |
Trong đó:
![]()
Và n = 0,468, U0 là tốc độ gió trung bình 1 giờ tại độ cao 10 m, đơn vị m/s và z là chiều cao trên mực nước biển có đơn vị mét. Việc sử dụng phổ có thể không được khuyến nghị khi trong cốc chế độ mà các ảnh hưởng ổn định là quan trọng. Tần số 1/2400 Hz xác định giới hạn thấp hơn với dải áp dụng của phổ Frøya. Bất cứ khi nào ước lượng mức năng lượng trong dải tần số thấp của phổ gió trên mặt nước, phổ Frøya tốt hơn các phổ dựa trên các nghiên cứu trên mặt đất là Davenport, Kaimal và Harris, và do đó nên được áp dụng ưu tiên với phổ này.
Tần số 1/2400 Hz xác định phạm vi ứng dụng của phổ Frøya, tương ứng với khoảng thời gian 40 phút. Đối với các phản ứng theo chu kỳ tự nhiên của phổ này, sự tắt dần (damping) là khá nhỏ, và thời gian duy trì của quá trình phản ứng gồm nhiều chu kỳ phản ứng. Vì quá trình tốc độ gió ngẫu nhiên luôn không ổn định trong các khoảng thời gian 2 đến 3 giờ, phương pháp phổ gió có thể không cần thiết phải được sử dụng cho các tải trọng gió trên các cấu trúc có tần số tự nhiên gần với tần số giới hạn 1/2400 Hz của phổ gió.
5.3.5 Quá trình tốc độ gió và vùng tốc độ gió
5.3.5.1 Các mô men phổ hữu dụng khi đại diện cho quá trình tốc độ gió U (t), trong đó U đại diện cho tốc độ gió tức thời tại thời điểm t, mô men phổ thứ j được định nghĩa như sau:
|
| (37) |
Độ lệch chuẩn của quá trình tốc độ gió được lấy bằng σU = ![]() .
.
5.3.5.2 Trong điều kiện ngắn hạn, như với một chu kỳ 10 phút, quá trình tốc độ gió U(t) thường được biểu diễn như một quá trình Gaussian, điều kiện theo một tốc độ gió trung bình đặc trưng 10 phút U10 và một độ lệch chuẩn σU. Tốc độ gió tức thời tại một điểm được xem xét sẽ theo một phân phối chuẩn với giá trị trung bình U10 và độ lệch chuẩn σU. Điều này thường xảy ra đối với những biến động ở địa hình đồng nhất. Tuy nhiên, đối với sự chảy rối tại nơi có địa hình phức tạp, một hệ số lệch (skewness) có giá trị phổ biến -0,1, có nghĩa giả thuyết Gaussian có độ lệch không sẽ không hoàn toàn được thực hiện. Độ lệch của quá trình tốc độ gió là mô men bậc 3 của dao động tốc độ gió chia cho ![]() .
.
5.3.5.3 Mặc dù quá trình tốc độ gió ngắn hạn có thể là Gaussian đối với địa hình đồng nhất, nhưng thường không phải là một quá trình Gaussion dải hẹp. Điều này quan trọng cho việc dự đoán giá trị cực đại của tốc độ gió và các phân phối xác suất có thể được thể hiện bằng mô men phổ.
5.3.5.4 Tại bất kỳ thời điểm sẽ có sự thay đổi tốc độ gió từ một điểm đến điểm khác trong không gian. Hai điểm càng gần nhau, sự tương quan giữa các tốc độ gió tương ứng càng cao. Tốc độ gió sẽ hình thành một vùng ngẫu nhiên trong không gian. Hàm tương quan cho vùng tốc độ gió có thể được biểu diễn như sau:
|
| (38) |
Trong đó r là khoảng cách giữa hai điểm, f là tần số, SU(f) là mật độ năng lượng phổ và Coh(r, f) là phổ kết dính. Phổ kết dính Coh(r, f) là một tần số phụ thuộc các kết nối không gian của tốc độ gió và biểu diễn sự tương quan giữa mật độ năng lượng phổ tại tần số f ở hai điểm cách nhau một khoảng r trong không gian.
5.3.5.5 Đà gió Lu là một thông số trong các mô hình của mật độ năng lượng phổ, được định nghĩa bằng:
|
| (39) |
Và có sự khác nhau theo chiều dọc, ngang và tách đứng.
5.3.5.6 Nếu dữ liệu không chỉ ra sự khác biệt, phổ kết dính có thể được đại diện bởi một phổ mô hình. Mô hình kết dính được sử dụng phổ biến nhất được nêu trong 5.3.5.7 đến 5.3.5.17
5.3.5.7 Phổ kết dính Davenport:
|
| (40) |
Trong đó r là khoảng chia, u là tốc độ gió trung bình trên khoảng cách r, f là tần số và c là hằng số phân rã không thứ nguyên. Độ giảm gắn kết c không phải hằng số nhưng phụ thuộc vào khoảng cách r và khoảng cách theo chiều dọc, đứng, ngang. Độ giảm gắn kết thường tăng theo khoảng cách, do đó chỉ ra sự phân rã nhanh hơn của độ gắn kết tương ứng với tần số tại các khoảng cách lớn hơn. Đối với gió bất ổn và khoảng cách đứng trong phạm vi 10 m đến 20 m, độ giảm gắn kết nằm trong khoảng 18 đến 28 được khuyến nghị.
5.3.5.8 Phổ kết dính Davenport được đề xuất ban đầu cho gió rối dọc, như các dao động tốc độ gió theo chiều dọc, và các khoảng cách đứng. Việc áp dụng phổ kết dính Davenport cho gió rối với các khoảng cách ngang đòi hỏi sự giảm gắn kết lớn hơn khi kết hợp với các khoảng cách đứng.
5.3.5.9 Không thích hợp để mở rộng việc áp dụng phổ kết dính Davenport với các thành phần bất ổn bên và đứng, khi phổ kết dính Davenport với giá trị giới hạn 1,0 cho f = 0 không đưa vào tính toán sự giảm kết dính tại các tần số thấp cho 2 thành phần bất ổn đó.
5.3.5.10 Sự hạn chế của mô hình Davenport là không vi phân được khi r = 0. Do dòng chảy tách, giá trị giới hạn của độ kết dính thực khi r = 0 thường được lấy với một giá trị nhỏ hơn 1,0 trong khi mô hình Davenport thường dẫn đến độ kết dính 1.0 khi r = 0.
5.3.5.11 Phổ kết dính IEC
|
| (41) |
trong đó r là khoảng cách, u là tốc độ gió trung bình trên khoảng cách r, f là tần số, và a, b là hằng số không thứ nguyên. LC là thông số quy đổi độ kết dính, liên quan tới chiều dài quy đổi Lu do LC = 0,742 Lu. Ngoại trừ tại các tần số rất thấp, a = 8,8 và b = 0,12 được khuyến nghị áp dụng cho gió rối theo chiều dọc và khoảng cách r theo chiều đứng và chiều ngang nằm trong khoảng 7 m đến 15 m.
5.3.5.12 Đối với độ kết dính gió dọc có khoảng cách r lớn, mô hình IEC với các giá trị hệ số có thể dẫn đến độ kết dính dự đoán lệch đáng kể so với độ kết dính thực, đặc biệt ở tần số thấp.
5.3.5.13 Mô hình kết dính đẳng hướng von Karman:
|
| (42) |
cho thành phần gió rối dọc có khoảng cách r theo phương ngang cũng như dọc.
5.3.5.14 Đối với thành phần rối ngang và khoảng cách ngang r, mô hình kết dính:
|
| (43) |
Công thức cũng áp dụng cho thành phần rối đứng với khoảng cách đứng r.
5.3.5.15 Đối với thành phần rối theo phương đứng và khoảng cách ngang r, mô hình kết dính:
|
| (44) |
Công thức này cũng áp dụng cho thành phần rối bên với khoảng cách đứng r.
Trong công thức này:
![]()
![]()
![]()
L là tỷ lệ chiều dài tương ứng với đà gió Lu do L = 0,742 Lu, Γ biểu diễn hàm Gamma và
Kv () biểu diễn hàm Bessel biển đối bậc v.
5.3.5.16 Mô hình kết dính von Karman dựa trên các giả định về tính đồng nhất, đẳng hướng và bất ổn. Mô hình kết dính von Karman đưa ra một đại diện cho cấu trúc gắn kết của các thành phần bất ổn theo phương ngang, dọc và đứng. Đối với các khoảng cách đứng, việc đo đạc chỉ ra rằng mô hình có thể không đúng, có thể do sự thiếu hụt đẳng hướng do mất ổn định đứng. Với các khoảng cách lớn, vượt quá 20 m, mô hình kết dính von Karman dẫn đến việc đánh giá cao độ kết dính.
5.3.5.17 Mô hình kết dính Frøya được phát triển cho gió trên mặt nước và biểu diễn độ kết dính của các dao động tốc độ gió theo phương ngang giữa 2 điểm trong không gian là:
|
| (45) |
trong đó U0 là tốc độ gió trung bình 1 giờ và ∆ là khoảng cách giữa 2 điểm mà tọa độ của chúng là (x1, y1, z1,) và (x2, y2, z2). x1 và x2 là tọa độ gió dọc, y1 và y2 là tọa độ gió ngang, và z1 và z2 là độ cao trên mực nước tĩnh. Hệ số Ai được tính bằng:
|
| (46) |
Với:
![]()
Và H = 10 m là độ cao tham chiếu. Các hệ số α, pi, qi, ri và các thành phần khoảng cách
∆i,i = 1,2,3 được cho trong Bảng 2.
Các hệ số của phổ kết dính Frøya
Bảng 2 - Các hệ số của phổ kết dính Frøya
| i | ∆i | qi | pi | ri | αi |
| 1 | |x2 - x1| | 1,00 | 0,4 | 0,92 | 2,9 |
| 2 | |y2 - y1| | 1,00 | 0,4 | 0,92 | 45,0 |
| 3 | |z2 - z1| | 1,25 | 0,5 | 0,85 | 13,0 |
5.3.5.18 Mô hình rối mô phỏng vùng gió có thể được áp dụng để thay thế cho các vùng gió rối bởi phương pháp mô hình mật độ năng lượng phổ và mô hình kết dính. Mô hình này được dựa trên một mô hình ten xơ phổ cho bất ổn bề mặt không khí của tốc độ gió cao và cho phép mô phỏng vùng 2 và 3 chiều của một, hai hoặc ba thành phần dao động vận tốc gió. Mô hình Mann được sử dụng rộng rãi cho thiết kế turbine gió.
5.3.6 Đường biểu đồ gió và độ ổn định khí quyển
5.3.6.1 Đường biểu đồ gió thay đổi theo độ cao của tốc độ gió và phụ thuộc nhiều vào các điều kiện ổn định của khí quyển. Thậm chí trong 24 giờ, đường biểu đồ gió gió thay đổi giữa ngày và đêm.
5.3.6.2 Đường biểu đồ gió có thể được bắt nguồn từ mô hình lô-ga-rit được nêu trong 5.3.2.4, và được điều chỉnh bởi hệ số ổn định. Đường biểu đồ gió gió lô-ga-rít theo hệ số điều chỉnh ổn định:
|
| (47) |
Trong đó ѱ là hàm phụ thuộc độ ổn định, dương khi điều kiện không ổn định, âm khi điều kiện ổn định và bằng 0 khi điều kiện trung tính. Điều kiện không ổn định thường được áp dụng khi mặt phẳng bị làm nóng và sự hòa trộn theo phương đứng tăng lên. Điều kiện ổn định áp dụng khi mặt phẳng bị làm lạnh, như trong đêm và sự hòa trộn theo phương đứng bị nén. Hình 3 chỉ ra các ví dụ về profile gió lô-ga-rit theo hệ số điều chỉnh ổn định cho các điều kiện thay đổi tại một địa điểm đặc trưng.
5.3.6.3 Hàm ổn định ѱ phụ thuộc phương pháp ổn định không thứ nguyên z = z/LMO, trong đó z là chiều cao và LMO là chiều dài Monin-Obukhov. Hàm ổn định có thể được tính toán từ các công thức:
| ѱ = -4,8z khi z ≥ 0 | (48) |
| ѱ = 2ln(1+x)+ln(1+x2)-2 tan-1(x) khi z < 0 | (49) |
Trong đó x = (1-19,3z)1/4
5.3.6.4 Chiều dài Monin-Obukhov LMO phụ thuộc vào dòng nhiệt nhạy cảm và ẩn nhiệt và phụ thuộc vào động lượng theo vận tốc ma sát u*. Giá trị của nó phản ảnh sự ảnh hưởng tương ứng của cơ học và nhiệt lên sự bất ổn. Các giá trị đặc trưng cho chiều dài Monin-Obukhov LMO được cho trong Bảng 3.
Bảng 3 - Chiều dài Monin-Obukhov
| Các điều kiện khí quyển | LMO (m) |
| Các ngày có sự đối lưu mạnh | -10 |
| Ngày có gió với sự gia nhiệt bởi mặt trời | -100 |
| Ngày có gió nắng ít | -150 |
| Không có sự bất ổn theo phương đứng | 0 |
| Bất ổn cơ học hoàn toàn | ∞ |
| Đêm có nhiệt độ phân tầng hãm sự bất ổn cơ học | > 0 |
| Đêm có nhiệt độ phân tầng ngăn sự bất ổn cơ học | >>0 |
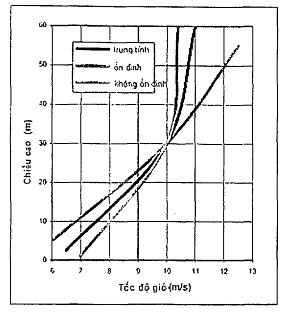
Hình 3 - Các ví dụ về đường biểu đồ gió cho các điều kiện trung tính, ổn định, không ổn định
5.3.6.5 Số Richardson R là một thông số không thứ nguyên mà giá trị của nó xác định sự đối lưu là tự do hay bị cưỡng bức:
|
| (50) |
Trong đó: g là gia tốc trọng trường, ρ0 là mật độ không bị nhiễu loạn, d ρ0/dz là gradient tỷ trọng đứng và dU / dz là gradient đứng của tốc độ gió ngang. R có giá trị dương khi không khí ổn định, ví dụ khi dòng nóng hướng xuống, và R có giá trị âm khi không khí không ổn định, ví dụ khi dòng nóng đi lên.
5.3.6.6 Khi dữ liệu cho số Richardson là có sẵn, mối quan hệ kinh nghiệm có thể được sử dụng để thu được chiều dài Monin-Obukhov:
![]() khi không khí bất ổn;
khi không khí bất ổn;
![]() khi không khí ổn định;
khi không khí ổn định;
5.3.6.7 Khi dữ liệu cho số Richardson R không có sẵn, số Richardson có thể được tính từ điều kiện trung bình như sau:
|
| (51) |
trong đó g là gia tốc trọng trường, T là nhiệt độ,γ = -∂T/∂z là gradient nhiệt độ và γd ≈ 9,8°C/km là gradient đoạn nhiệt khô. ∂u/∂z và ![]() là gradient đứng của hai thành phần tốc độ gió trung bình theo phương ngang
là gradient đứng của hai thành phần tốc độ gió trung bình theo phương ngang ![]() và
và ![]() ; z là chiều cao đứng. Tỷ số Bowen B của độ nhạy nhiệt ẩn tại mặt phẳng gần mặt đất có thể lấy xấp xỉ:
; z là chiều cao đứng. Tỷ số Bowen B của độ nhạy nhiệt ẩn tại mặt phẳng gần mặt đất có thể lấy xấp xỉ:
|
| (52) |
Trong đó cp là nhiệt dung, LMO là chiều dài Monin-Obukhov, ![]() và
và ![]() là nhiệt độ trung bình tại 2 mức 1 và 2, tương ứng với
là nhiệt độ trung bình tại 2 mức 1 và 2, tương ứng với ![]() , và
, và ![]() là độ ẩm riêng. Độ ẩm riêng q được tính toán như độ ẩm riêng phần.
là độ ẩm riêng. Độ ẩm riêng q được tính toán như độ ẩm riêng phần.
5.3.6.8 Việc áp dụng thuật toán trong 5.3.6.7 yêu cầu giả thiết ban đầu cho LMO. Việc lặp lại là cần thiết cho việc xác định số Richardson R. Sự hội tụ đạt được khi việc tính toán số Richardson R dẫn đến chiều dài Monin-Obukhov LMO bởi các công thức trong 5.3.6.6 bằng giá trị của LMO.
5.3.6.9 Các đặc điểm địa hình như đồi, núi, dốc đứng ảnh hưởng lên tốc độ gió. Các lớp của dòng gió sẽ tăng tốc gần các địa hình đó và profile gió trở nên thay đổi.
5.4.1 Quy định chung
5.4.1.1 Khi tốc độ gió hoặc hướng gió thay đổi, các điều kiện gió nhất thời có thể xảy ra. Điều kiện gió nhất thời bản chất nằm ngoài các đại diện của điều kiện gió tĩnh. Điều kiện gió nhất thời là:
- Gió giật (gusts);
- Tố lốc (squalls);
- Cực đại của gradient tốc độ gió (extremes of wind speed gradients);
- Gió cắt mạnh (strong wind shears);
- Các thay đổi cực đại theo hướng gió (extreme changes in wind direction);
- Các thay đổi đồng thời tốc độ và hướng gió.
5.4.2 Gió giật (Gusts)
5.4.2.1 Gió giật (gusts) là gió có tốc độ tăng đột ngột, đặc trưng bởi thời gian nhỏ hơn 20 giây, và sau đó gió lặng xuống. Gió giật đặc trưng bởi thời gian thiết lập, độ lớn, và khoảng thời gian.
5.4.2.2 Gió giật xảy ra như một phần dao động tự nhiên của tốc độ gió với chu kỳ 10 phút của các điều kiện gió tĩnh, mà không thay đổi mức độ tốc độ gió trung bình - không cần thiết phải xem xét các điều kiện gió nhất thời, nhưng gió giật là các giá trị cực đại của quá trình tốc độ gió tĩnh.
5.4.3 Tố lốc (Squalls)
5.4.3.1 Tố lốc được đặc trưng bởi một đợt gió đột ngột, trong khoảng thời gian 10 đến 60 phút, và sau đó tốc độ đột ngột giảm. Tố lốc làm thay đổi mức tốc độ gió trung bình.
5.4.3.2 Tố lốc do không khí lạnh kết hợp với thời tiết cực đoan như giông bão. Sự hình thành gió mạnh liên quan đến sự mất ổn định khí quyển và tùy thuộc theo mùa. Tố lốc thường đi kèm với những thay đổi về hướng gió và độ giảm nhiệt độ không khí. Nhiệt độ không khí thay đổi có thể là một chỉ số tin cậy của một cơn gió mạnh.
5.4.3.3 Có nhiều sự không chắc chắn liên quan đến profile gió đứng và sự kết dính bên của Tố lốc. Profile gió đứng có thể chệch đáng kể so với các profile mô hình cho trong 5.3.2.4 và 5.3.2.8. Các profile giả định như profile tốc độ gió cho tốc độ gió trung bình cực đại Frøya được cho trong 5.3.2.13 là có khả năng. Tuy nhiên, giả định sẽ ảnh hưởng lên sự dự đoán tải trọng gió và có thể hay không bảo toàn.
6.1.1 Khái niệm
Sóng biển có hình dạng, chiều cao, chiều dài và vận tốc truyền ở dạng ngẫu nhiên, không theo quy luật. Trạng thái biển thực tế được mô tả tốt nhất bởi một mô hình sóng ngẫu nhiên.
Mô hình sóng ngẫu nhiên tuyến tính là tổng của nhiều con sóng tuyến tính nhỏ có biên độ, tần số và hướng khác nhau và các pha sóng là ngẫu nhiên.
Mô hình sóng ngẫu nhiên phi tuyến có tính đến tổng và yếu tố sóng tần số khác bởi tương tác phi tuyến giữa những yếu tố sóng riêng lẻ.
Các điều kiện sóng dùng cho mục đích thiết kế được miêu tả bởi cả lý thuyết sóng thiết kế tiền định hoặc lý thuyết ngẫu nhiên áp dụng cho phổ sóng.
Đối với phản ứng tựa tĩnh của kết cấu, chỉ cần sử dụng sóng điều hòa tiền định đặc trưng bởi bước sóng và chu kỳ sóng tương ứng, chiều cao sóng và chiều cao đỉnh sóng. Những thông số sóng tiền định được dự báo bởi các lý thuyết thống kê.
Các kết cấu có phản ứng động đáng kể cần đến mô hình ngẫu nhiên của bề mặt biển và động học biển xét trong các chuỗi thời gian. Một trạng thái biển được xác định rõ bởi một phổ tần số sóng với một chiều cao sóng đáng kể cho trước, một tần số đại diện, một hướng truyền trung bình và một hàm lan truyền. Trạng thái biển thường được giả định là một quá trình ngẫu nhiên cố định. Thời gian Tiêu chuẩn giữa những lần đo sóng thường là 3 giờ, nhưng khoảng thời gian cố định có thể dao động từ 30 phút đến 10 tiếng.
Những điều kiện sóng trong một trạng thái biển có thể chia thành hai loại: sóng do gió và sóng lừng. Sóng do gió được hình thành bởi gió địa phương. Sóng lừng không hình thành bởi gió địa phương. Sóng lừng là những con sóng được tiếp tục duy trì khỏi vùng chúng được tạo ra. Một vài thành phần sóng lừng có thể xuất hiện tại một địa điểm nhất định.
6.1.2 Đặc trưng chung của sóng
Sóng điều hòa lan truyền với hình dạng cố định, gồm một chiều dài riêng biệt, chu kỳ và chiều cao sóng.
Bước sóng: Bước sóng λ là khoảng cách giữa hai đỉnh sóng.
Chu kỳ sóng: Chu kỳ sóng T là khoảng thời gian giữa hai đỉnh sóng liên tục đi qua một điểm cụ thể.
Vận tốc pha sóng: Vận tốc truyền của dạng sóng được gọi là vận tốc pha sóng, tốc độ sóng và được biểu thị bằng c = λ / T.
Tần số sóng là nghịch đảo của chu kỳ sóng: f = 1 / T.
Tần số góc sống: ω = 2p / T.
Số sóng: k = 2p / λ .
Tung độ mặt sóng: Tung độ mặt sóng z = ƞ(x,y,t) là khoảng cách giữa mực nước tĩnh và mặt sóng.
Chiều cao đỉnh sóng AC là khoảng cách từ mực nước tĩnh đến đỉnh sóng.
Chiều sâu bụng sóng AT là khoảng cách từ mực nước tĩnh đến bụng sóng.
Chiều cao sóng: chiều cao sóng H là khoảng cách từ đỉnh đến bụng sóng T = AC + AT.
Việc phân tích những lý thuyết sóng được phát triển cho độ sâu nước không đổi d. Mục tiêu của một lý thuyết sóng là xác định mối quan hệ giữa T và λ và chuyển động của dòng nước.
Tương quan lan truyền sóng (dispersion relation) là quan hệ giữa chu kỳ sóng T, bước sóng λ và chiều cao sóng H với một độ sâu nước đã cho d.
Sóng phi tuyến điều hòa là sóng không đối xứng, có AC > AT và vận tốc pha sóng phụ thuộc vào chiều cao sóng.
Mật độ năng lượng trung bình E là tổng của trung bình động lực sóng và năng lượng tiềm năng trên một đơn vị diện tích ngang. Dòng năng lượng P là tỷ số trung bình của năng lượng truyền trên một đơn vị chiều rộng mặt phẳng vuông góc với hướng truyền của sóng. Nhóm vận tốc cg= P/E là tốc độ của năng lượng truyền sóng.
Trong sóng không điều hòa hoặc sóng ngẫu nhiên, cao độ mặt tự do z = ƞ(x,y,t) là một quá trình ngẫu nhiên. Bước sóng cục bộ của sóng không điều hòa được định nghĩa là khoảng cách giữa hai đỉnh cắt không liên tiếp. Đỉnh sóng và bụng sóng không đều được định nghĩa là giá trị lớn nhất giữa cao độ trung bình trên và dưới cùng mức.
6.2 Các lý thuyết sóng điều hòa
6.2.1 Tính ứng dụng của các lý thuyết sóng
Có ba thông số xác định lý thuyết sóng được áp dụng trong một trường hợp cụ thể. Đó là chiều cao sóng H, chu kỳ sóng T và độ sâu nước d. Những thông số này được sử dụng để xác định ba thông số không thứ nguyên xác định phạm vi sử dụng của các lý thuyết sóng khác nhau:
Thông số bước sóng: ![]()
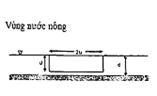
Thông số nước nông: ![]()
Số Ursell: ![]()
Trong đó λ0 và k0 là bước sóng nước sâu tuyến tính và số sóng tương ứng với chu kỳ sóng T
Ba thông số này không độc lập, khi hai thông số được cho trước, thông số thứ ba sẽ được xác định. Mối quan hệ được thể hiện:
|
| (53) |
Số Ursell cũng được xác định bằng:![]()
Phạm vi áp dụng của các lý thuyết sóng được cho trong Hình 5.
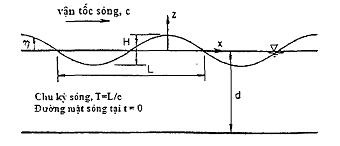
Hình 4 - Các đặc tính truyền sóng
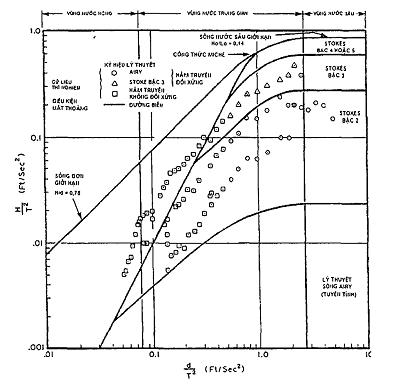
Hình 5 - Phạm vi áp dụng các lý thuyết sóng khác nhau
Trục hoành là giá trị độ sâu nước. Trục đứng là giá trị bước sóng.
6.2.2 Lý thuyết sóng tuyến tính
6.2.2.1 Lý thuyết sóng đơn giản nhất thu được bằng cách lấy chiều cao sóng nhỏ hơn nhiều so với bước sóng và độ sâu nước. Lý thuyết này được xem như lý thuyết sóng biên độ nhỏ, lý thuyết sóng tuyến tính, lý thuyết sóng hình sin (sinusoidal wave theory) hoặc lý thuyết sóng Airy.
6.2.2.2 Đối với sóng tuyến tính điều hòa, chiều cao đỉnh sóng AC bằng chiều cao bụng sóng AH và được biểu hiện với biên độ sóng A, H = 2 A.
Tung độ mặt sóng được xác định bởi:
|
| (54) |
Trong đó: Q = k(xcos β + ysinβ)-ωt là pha và β là hướng truyền, đo từ trục x dương; c là vận tốc pha.
6.2.2.3 Sự tán sắc của sóng đưa ra mối quan hệ giữa chu kỳ sóng T và bước sóng λ. Đối với sóng tuyến tính tại độ sâu nước hữu hạn T:
|
| (55) |
Liên quan đến tần số góc ω = 2p / T và số con sóng k = 2p / λ, quan hệ tán sắc của sóng:
|
| (56) |
6.2.2.4 Công thức gần đúng cho bước sóng λ như là một hàm của chu kỳ sóng T:
|
| (57) |
Trong đó:
![]() và α1 = 0,666; α2 = 0,445; α3 = -0,105; α4 = 0,272
và α1 = 0,666; α2 = 0,445; α3 = -0,105; α4 = 0,272
Hình 6 đưa ra bước sóng như một hàm của chu kỳ cho những độ sâu nước khác nhau.
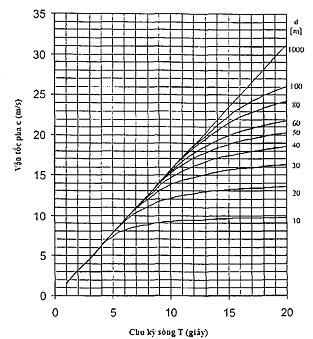
Hình 6 - Bước sóng và vận tốc pha như một hàm của chu kỳ sóng tại các độ sâu nước đối với sóng tuyến tính
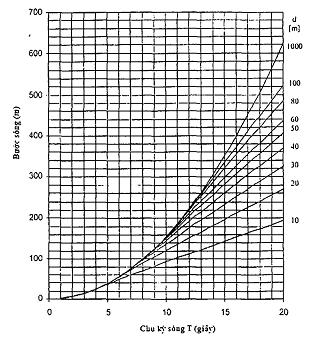
Hình 6 - Bước sóng và vận tốc pha như một hàm của chu kỳ sóng tại các độ sâu nước đối với sóng tuyến tính (kết thúc)
6.2.2.5 Đối với sóng tuyến tính, vận tốc pha chỉ phụ thuộc bước sóng λ, không phụ thuộc biên độ A
|
| (58) |
Hình 6 thể hiện vận tốc pha như một hàm của chu kỳ sóng cho những độ sâu khác nhau.
6.2.2.6 Đối với độ sâu nước ![]() công thức được đơn giản hóa:
công thức được đơn giản hóa:
|
| (59) |
Và tương quan lan truyền sóng được đơn giản hóa thành:
![]() hay λ = 1,56T2 với λ đơn vị là mét, T đơn vị là giây.
hay λ = 1,56T2 với λ đơn vị là mét, T đơn vị là giây.
Công thức cho sự đổi chỗ phần tử chất lỏng, vận tốc, gia tốc chất lỏng và áp lực bề mặt chất lỏng trong sóng tuyến tính và sóng bậc 2 được cho trong Bảng 4.
6.2.3 Lý thuyết sóng Stokes
6.2.3.1 Sóng mở rộng Stokes là một sự mở rộng của tung độ mặt sóng phụ thuộc vào chiều cao sóng tuyến tính H. Sóng Stokes bậc một tương tự với sóng tuyến tính, hoặc sóng Airy.
6.2.3.2 Profile tung độ mặt sóng đối với sóng Stoke điều hòa bậc 2 có dạng:
|
| (60) |
Trong đó: Q = k(xcosβ + ysinβ)-ωt
6.2.3.3 Trong vùng nước sâu, sóng Stokes bậc 2 có dạng:
|
| (61) |
6.2.3.4 Sóng Stokes bậc 2 và bậc cao hơn là không đối xứng với AC > AT. Đỉnh sóng dốc và đảy sóng mở rộng hơn sóng Airy.
Đối với sóng Stokes bậc 2 ở vùng nước sâu:
|
| (62) |
|
| (63) |
Do đó, chiều cao đỉnh sóng tăng lên bằng một hệ số 1 + pH / 2λ so với sóng tuyến tính Airy. Tương quan lan truyền sóng tuyến tính giữ cho các sóng Stockes bậc 2, từ đó các vận tốc pha c và bước sóng λ duy trì độc lập với chiều cao sóng.
6.2.3.5 Tuy nhiên với sóng Stokes bậc 3, vận tốc pha sóng phụ thuộc vào chiều cao sóng:
|
| (64) |
Đối với vùng nước sâu ![]() công thức có dạng:
công thức có dạng:
|
| (65) |
Công thức cho sự đổi chỗ phần tử chất lỏng, vận tốc, gia tốc chất lỏng và áp lực bề mặt chất lỏng đối với sóng Stokes bậc 2 được cho trong Bảng 4.
6.2.3.6 Đối với những sóng điều hòa có độ dốc S < Smax (và số Ursell UR < 30), lý thuyết sóng Stokes bậc 5 được áp dụng. Tỷ lệ lớn nhất của đỉnh sóng và chiều cao sóng là 0,635.
Lý thuyết sóng Stokes không áp dụng cho vùng nước nông, khi UR > 30 lý thuyết sóng Cnoidal hoặc lý thuyết hàm dòng nên được sử dụng.
Khi UR ~ 30, cả lý thuyết sóng Stokes bậc 5 và lý thuyết sóng cnoidal đều có sự không chính xác. Trong những trường hợp sóng điều hòa, nguyên lý hàm dòng được khuyến cáo sử dụng.
6.2.4 Lý thuyết sóng Cnoidal
Sóng Cnoidal là sóng có chu kỳ, có đỉnh sóng rõ rệt được chia bởi bụng sóng rộng. Lý thuyết sóng Cnoidal được sử dụng khi μ < 0,125 và UR > 30. Sóng Cnoidal có tỷ lệ đỉnh sóng và chiều cao sóng trong khoảng 0,635 và 1.
6.2.5 Lý thuyết sóng đơn
Đối với những số Ursell cao, bước sóng của sóng Cnoidal là vô cực và sóng là sóng đơn. Sóng đơn là sóng truyền tại vùng nước nông nơi tung độ mặt sóng nằm toàn bộ trên mực nước trung bình, do đó AC = H. Profile sóng đơn có thể tính gần đúng bằng:
|
| (66) |
Trong đó ε = H / d. Vận tốc pha sóng ![]()
6.2.6 Lý thuyết sóng hàm dòng
Lý thuyết sóng hàm dòng là một quy trình phân tích toán học cho việc tính gần đúng một profile sóng và có phạm vi áp dụng rộng hơn các lý thuyết sóng kể trên.
Nghiệm của hàm truyền có dạng cơ bản:
|
| (67) |
Trong đó: c là vận tốc pha sóng, N là bậc của lý thuyết sóng. Bậc N của lý thuyết hàm truyền được xác định bởi thông số độ dốc sóng S và thông số nước nông μ. Khi N = 1, lý thuyết hàm truyền trở thành lý thuyết sóng tuyến tính.
Tiệm cận gần đến chiều cao sóng vỡ, có nhiều yêu cầu cần cung cấp để cho ra một đại diện chính xác của sóng.
6.3.1 Động học sóng điều hòa
6.3.1.1 Đối với sóng điều hòa xác định có chu kỳ T, chiều cao sóng H và độ sâu nước d, động lực sóng đều theo 2 phương có thể được tính toán bằng một lý thuyết sóng tương đương hợp lý với những thông số sóng đã cho.
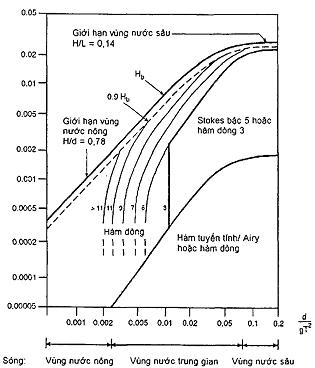
Hình 7 - Lý thuyết sóng hàm truyền bậc N sao cho độ lệch vận tốc và gia tốc lớn nhất ít hơn 1%
6.3.1.2 Sóng tuyến tính và sóng Stokes dựa trên lý thuyết nhiễu loạn và trực tiếp đưa ra động học sóng dưới cao độ z = 0. Động học sóng giữa đỉnh sóng và mực nước tỉnh có thể xác định bằng lý thuyết mở rộng hoặc ngoại suy được miêu tả trong 6.3.3. Lý thuyết hàm truyền 6.2.6 cung cấp động học sóng cho tất cả trường đến tung độ mặt tự do.
6.3.2 Mô hình hóa sóng không điều hòa
6.3.2.1 Sóng ngẫu nhiên không điều hòa, đại diện cho một trạng thái biển, có thể được mô hình như một tổng của các sóng hình sin. Mô hình sóng ngẫu nhiên đơn giản nhất là mô hình sóng tuyến tính đỉnh sóng dài:
|
| (68) |
trong đó: εk là pha ngẫu nhiên phân phối đều trong khoảng 0 và 2p, độc lập với nhau và các biên độ ngẫu nhiên Ak được lấy theo phân phối Rayleigh với giá trị bình phương trung bình bằng:
|
| (69) |
S(ω) là phổ sóng và ∆ωk = ωk - ωk-1 là hiệu số giữa những tần số liên tiếp.
6.3.2.2 Khoảng tần số thấp nhất ∆ω được điều chỉnh bởi tổng thời gian mô hình hóa t, ∆ω = 2pλ
Số lượng tần số để mô hình hóa điều kiện biển điển hình ngắn hạn ít nhất nên lấy là 1000 tần số. Ảnh hưởng của tần số lớn nhất ωmax nên được kiểm tra. Điều này là đặc biệt quan trọng khi mô phỏng vận tốc chất lỏng không điều hòa.
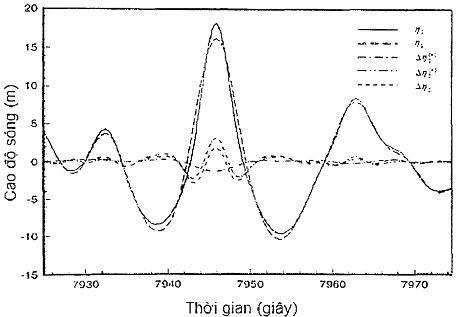
Hình 8 - Mô hình sóng không điều hòa bậc 1 và bậc 2; Hs = 15,5 m, Tp = 17,8 s, γ = 1,7. N = 21 600, ∆t = 0,5 s
6.3.2.3 Mô hình sóng ngẫu nhiên phi tuyến đơn giản nhất là mô hình bậc 2 đỉnh sóng dài, trong đó phương pháp sóng bậc 2 có N2 là hiệu chỉnh độ lệch trên toàn bộ tổng các tần số và tất cả các tất số khác. Sóng ngẫu nhiên bậc 2 được mô hình hóa là ƞ2 = ƞ1 + ∆ƞ2, trong hiệu chỉnh bậc 2 được xác định bởi:
![]() (70)
(70)
Trong đó ![]() là bình phương hàm truyền tung độ mặt sóng. Trong vùng nước sâu:
là bình phương hàm truyền tung độ mặt sóng. Trong vùng nước sâu:
|
| (71) |
|
| (72) |
Độ lớn tương đối giữa phân phối bậc 1 và bậc 2 đến cao độ mặt tự do được chỉ ra trong Hình 8.
6.3.2.4 Mô hình bậc hai được thể hiện để phù hợp dữ liệu thực nghiệm nếu một tần số đạt ngưỡng giới hạn ![]() được áp dụng. Mô hình sóng ngẫu nhiên bậc cao vẫn đang được phát triển cho những ứng dụng đặc biệt.
được áp dụng. Mô hình sóng ngẫu nhiên bậc cao vẫn đang được phát triển cho những ứng dụng đặc biệt.
6.3.3 Động học sóng không điều hòa
Động học trong sóng không điều hòa có thể được dự đoán bởi một trong các nguyên lý sau:
- Nguyên lý Grue;
- Nguyên lý Wheeler;
- Mô hình động học bậc 2.
Cách đơn giản để xác định động học dưới đỉnh sóng của con sóng lớn tại vùng nước sâu là nguyên lý Grue. Đối với một tung độ sóng theo chuỗi thời gian, bằng việc đo đạc hay mô phỏng, chiều cao đỉnh sóng và chu kỳ bụng sóng tới bụng sóng tương ứng TTT được xác định. Tần số góc cục bộ được xác định bằng ω = 2p / TTT. Số sóng tương ứng k và độ dốc sóng ε được tính toán bằng việc giải các phương trình số học tương ứng với sóng Stokes bậc 3:
|
| (73) |
Công thức đầu tiên là quan hệ tán sắc phi tuyến và công thức thứ hai là công thức không thứ nguyên cho cao độ mặt tự do. Vận tốc ngang dưới đỉnh sóng được cho bởi hàm mũ:
|
| (74) |
Trong đó: z = 0 là mực nước trung bình và g là gia tốc trọng trường. Nguyên lý Grue giới thiệu phía trên bị giới hạn với động lực đỉnh sóng và có giá trị cho sóng vùng nước sâu.
6.3.3.1 Nguyên lý Wheeler mở rộng được sử dụng rộng rãi. Nguyên lý dựa trên sự quan sát vận tốc chất lỏng tại mực nước tĩnh bị giảm yếu so với lý thuyết tuyến tính. Nguyên tắc cơ bản là ghi lại dữ liệu từ cao độ mặt tự do, tính toán vận tốc cho từng tần số sử dụng lý thuyết tuyến tính và cho từng thời điểm trong chuỗi thời gian, trục dọc được kéo dài theo biểu thức:
|
| (75) |
Trong đó ƞ là tung độ mặt tự do và d là độ sâu nước (Hình 9)
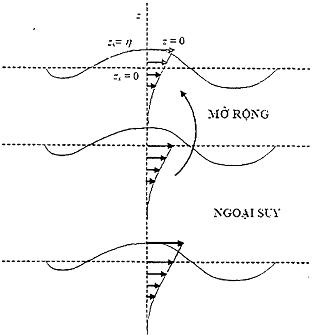
Hình 9 - Profile mở rộng và ngoại suy của vận tốc
6.3.3.2 Nguyên lý Wheeler phải được sử dụng với một bản ghi tung độ phi tuyến (được đo đạc hoặc bậc 2) và những thành phần động học phi tuyến nếu chúng độc lập.
Các vận tốc theo phương ngang có thể thống nhất mô hình hóa lên cao độ mặt tự do bằng việc sử dụng một mô hình động học Taylor mở rộng bậc 2 (ngoại suy) của profile vận tốc tuyến tính gồm những phần từ tổng những thành phần tần số sóng khác nhau. Vận tốc theo phương ngang tại chiều cao z dưới đỉnh sóng cho bởi:
| u(z) = u(1)(z) + u(2+)(z) + u(2-)(z); z ≤ 0 | (76) |
| u(z) = u(1)(0) + (∂u(1) / ∂z)|z=0 z + u(2+)(0) + u(2-)(0); z > 0 | (77) |
Trong đó u(1)(z), u(2+)(z), u(2-)(z) là profile vận tốc tuyến tính, profile tổng vận tốc bậc 2 và profile vận tốc với các tần số khác nhau. Công thức tương tự đối với vận tốc đứng và gia tốc/ ngang và đứng, cần lưu ý khi tính toán lực tác động lên ống đứng được gắn lên vật nổi, động học phải phù hợp với lý thuyết sóng sử dụng cho tính toán sự chuyển động của vật nổi.
6.3.3.3 Khi sử dụng một bản ghi đo đạc đầu vào, một bộ lọc thấp phải được áp dụng để tránh những tần số quá cao. Được khuyên sử dụng một tần số phân cắt bằng 4 lần tần số đỉnh phổ.
6.3.3.4 Hệ số động học sóng
Khi sử dụng sóng thiết kế theo 2 phương cho việc tính toán lực tác động lên phần tử kết cấu, vận tốc, gia tốc hạt sóng có thể bị giảm yếu bằng việc đưa vào tính toán sự truyền hướng thực tế của sóng không điều hòa. Hệ số giảm yếu được biết đến là hệ số động học sóng được định nghĩa là tỷ số giữa giá trị quân phương của vận tốc dòng và giá trị quân phương của vận tốc trong vùng biển theo một phương duy nhất.
Hệ số động học sóng có thể cho như sau:
|
| (78) |
đối với hàm truyền hướng D(θ) ~ cosn(θ) được định nghĩa trong 6.5.8.4 hoặc bằng:
|
| (79) |
đối với hàm truyền hướng D(θ) ~ cos2s(θ / 2) được định nghĩa trong 6.5.8.7
6.4.1 Quy định chung
Những lý thuyết sóng được phát triển cho độ sâu nước không đổi có thể được sử dụng để dự đoán sự biến dạng các tính chất sóng khi sóng truyền về bờ từ vùng nước sâu đến nước nông. Chu kỳ sóng T không đổi trong khi tốc độ pha c và bước sóng λ giảm, chiều cao sóng H và độ dốc sóng S tăng lên.
6.4.2 Hiệu ứng nước nông (Shoaling)
Đối với chuyển động hai chiều, chiều cao sóng tăng theo công thức:
|
| (80) |
trong đó Ks là hệ số nước nông và cg vận tốc nhóm:
|
| (81) |
Và số sóng k có liên quan với chu kỳ sóng T bởi quan hệ khúc xạ. Kí hiệu 0 chỉ đến giá trị độ sâu nước tại độ sâu nước d = d0.
6.4.3 Sự khúc xạ (Refraction)
Tốc độ pha thay đổi như một hàm của độ sâu nước d. Vì thế, đối với sóng tiếp cận đường đẳng sâu tại một góc khác lớn hơn bình thường, độ sâu nước sẽ thay đổi dọc theo đỉnh sóng. Kết quả đỉnh sóng có xu hướng uốn cong về đường đẳng sâu và đỉnh sóng có xu hướng song song với đường bờ biển.
Đối với những đường đồng mức mặt biển song song, luật khúc xạ Snell áp dụng:
|
| (82) |
Trong đó: c = c(kd) là vận tốc pha và α là góc giữa tia sóng và đường vuông góc với đường đồng mức mặt biển. Sự khúc xạ cũng có ảnh hưởng lên biên độ sóng. Đối với những đường đồng mức độ sâu song song với đường bờ biển, sự thay đổi của chiều cao sóng được cho bởi:
|
| (83) |
trong đó: Ks là hệ số nước nông được cho trong 6.4.2 và Kr là hệ số khúc xạ được xác định bằng:
|
| (84) |
Trong đó α0 là góc giữa đỉnh sóng và đường đồng mức độ sâu.
6.4.4 Sự phản xạ sóng (Wave reflection)
Khi mặt sóng gặp phải một lớp dưới bề mặt hoặc mặt phẳng chắn đứng, một phần của năng lượng sẽ bị phản xạ lại. Những sóng điều hòa trở thành sóng đứng khi chiều cao sóng H truyền vuông góc với một bề mặt tường đứng vô hạn.
Cao độ bề mặt tự do đối với những sóng đứng tuyến tính lên mặt tường đứng được cho bởi:
| ƞ = Hcos(kx)cos(ωt) | (85) |
Áp lực lên tường chắn được cho bởi:
|
| (86) |
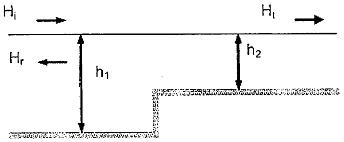
Hình 10 - Những con sóng vượt qua tường chắn dưới nước - độ sâu nước thay đổi từ h1 đến h2
Hệ số phản xạ R = Hr /Hi được định nghĩa là tỷ số của chiều cao sóng phản xạ với chiều cao sóng tới. Đối với sóng dài với bước sóng lớn hơn độ sâu nước, truyền từ một hướng tương đối đến đường vuông góc với tường chắn dưới nước, hệ số phản xạ được cho bởi:
|
| (87) |
Trong đó α = ki cosθi; k1 cosθi = k2 cosθ2; ![]()
ω là tần số sóng và kí hiệu 1,2 liên quan đến từng giá trị độ sâu 1 và 2
Hệ số truyền T = Ht / Hi được định nghĩa là tỷ lệ của chiều cao sóng truyền với chiều cao sóng tới
|
| (88) |
Khi h1 < h2 tổng phản xạ (R = 1) xảy ra với góc tới tới hạn:
|
| (89) |
Đối với những địa hình chung, các phương pháp số học phải được áp dụng.
6.4.5 Sóng đứng trong vịnh nước nông
Chu kỳ tự nhiên của sóng đứng trong vịnh nước nông với chiều dài L, chiều rộng B và độ sâu d là:
|
| (90) |
Chu kỳ tự nhiên của sóng đứng trong vùng vịnh tròn nước nông với bán kính α được cho bởi:
|
| (91) |
đối với phương pháp đối xứng và:
|
| (92) |
Đối với phương pháp bất đối xứng trong đó ![]() và
và ![]() là đạo hàm 0 theo thứ tự của J’0 và J’1 của hàm Bessel.
là đạo hàm 0 theo thứ tự của J’0 và J’1 của hàm Bessel.
6.4.6 Chiều cao sóng lớn nhất và sóng vỡ
6.4.6.1 Chiều cao sóng bị giới hạn bởi sự vỡ sóng. Chiều cao sóng lớn nhất Hb được cho bởi:
|
| (93) |
Trong đó λ là bước sóng tương ứng với độ sâu nước d. Trong vùng nước sâu, giới hạn sóng vỡ tương ứng với một độ dốc sóng lớn nhất Smax = Hb / λ = 1/7
6.4.6.2 Chiều cao sóng vỡ là một hàm của chu kỳ sóng đối với những độ sâu nước khác nhau được cho trong Hình 10. Trong vùng nước nông, giới hạn của chiều cao sóng có thể lấy bằng 0,78 lần độ sâu nước tại đó. Cần lưu ý rằng những con sóng khi truyền trên một mặt đáy biển ngang phẳng có thể vỡ do sóng có chiều cao thấp hơn. Dưới điều kiện lý tưởng, giới hạn sóng vỡ có thể bằng 0,55.
6.4.6.3 Kết cấu bờ hoặc kết cấu biển trong vùng nước nông yêu cầu một đánh giá chiều cao sóng lớn nhất đáng tin cậy.
6.4.6.4 Sóng vỡ được phân loại chung do tràn (spilling), dựng (plunging), trào (surging) hoặc sụp (collapsing). Sự hình thành nguyên nhân vỡ điển hình phụ thuộc vào thông số không thứ nguyên
|
| (94) |
trong đó Hb là chiều cao sóng vỡ, m là độ dốc bờ, và λ0 = gT2 / 2p là bước sóng tại vùng nước sâu, T là chu kỳ sóng. Đặc điểm của các nguyên nhân vỡ là:
Tràn (Spilling) - bọt sóng xuất hiện tại đỉnh sóng và tràn xuống mặt trước của sóng. Sóng vỡ do tràn thường tạo thành khi x < 0,4.
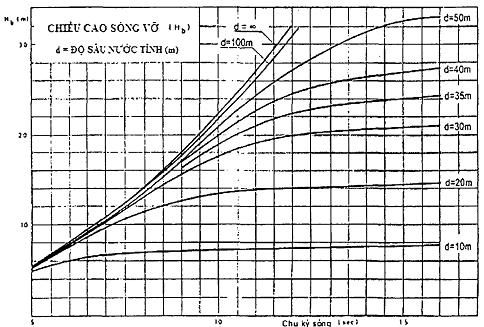
Hình 11 - Chiều cao sóng vỡ phụ thuộc vào độ sâu nước tĩnh
Dựng (Plunging) - Toàn bộ mặt trước của sóng dựng lên cho đến khi thẳng đứng và đổ xuống phần chân sóng. Sóng vỡ do đổ tạo thành khi 0,4 < xb< 2,0.
Trào (Surging) - xảy ra khi sóng truyền gần bờ biển dốc với bọt hình thành gần mặt bờ biển. Trào sóng tạo thành khi xb > 2,0.
Sụp (Collapsing) - phần thấp hơn mặt trước của đường sóng đến phương đứng, và mặt trước cong lên. Sóng vỡ do sụp là một dạng chuyển từ dựng và trào sóng, xb ~ 2,0.
6.5.1 Quy định chung
Mặt biển thường được giả thiết là tĩnh trong khoảng thời gian 20 phút từ 3 đến 6 tiếng. Điều kiện biển tĩnh được đặc trưng bởi một hệ nhưng thông số môi trường như chiều cao sóng đáng kể Hs và chu kỳ đỉnh Tp.
Chiều cao sóng đáng kể Hs được định nghĩa là giá trị trung bình của một phần ba số sóng có chiều cao lớn nhất trong tổng số các sống được thống kê trong một khoảng thời gian, cũng được hiểu là H1/3.
Chu kỳ đỉnh Tp là chu kỳ sóng được xác định bởi nghịch đảo của tần số tại đó phổ năng lượng sóng có giá trị lớn nhất.
Chu kỳ cắt không Tz là giá trị thời gian trung bình giữa 2 sóng cắt đường trung bình theo chiều đi lên của mực nước trung bình.
6.5.2 Phổ sóng
6.5.2.1 Trạng thái biển không điều hòa trong điều kiện ngắn hạn có thể được miêu tả bằng 1 phổ sóng. Đó là Hàm mật độ năng lượng phổ của lượng chiếm nước mặt biển theo phương đứng.
6.5.2.2 Phổ sóng được cho trong bảng mẫu, bằng việc đo đạc phổ hoặc bằng một công thức phân tích thông số. Hầu hết phổ thích hợp phụ thuộc vào địa hình với độ sâu nước cục bộ và mức độ của trạng thái biển
6.5.2.3 Phổ Pierson-Moskowitz (PM) và JONSWAP thường được áp dụng cho gió biển. Phổ PM được đề xuất ban đầu cho vùng biển phát triển hoàn toàn. Phổ JONSWAP mở rộng PM bao bồm bước sóng giới hạn, miêu tả sự phát triển của các trạng thái biển. Cả hai phổ miêu tả các điều kiện gió biển thường xảy ra trong phần lớn trạng thái biển khắc nghiệt.
6.5.2.4 Các trạng thái biển trung bình và thấp trong khu vực biển mở thường được tạo thành bởi cả gió biển và sóng lừng. Một phổ hai đỉnh (two peak spectrum) thường được sử dụng để áp dụng đối với cả hai dạng thời tiết đó. Phổ Ochi-Hubble và phổ Torsethaugen là phổ 2 đỉnh.
6.5.2.5 Mô men phổ mn với bậc chung n được định nghĩa như sau:
|
| (95) |
trong đó f là tần số sóng, n = 0,1,2,…
6.5.2.8 Nếu mật độ năng lượng phổ S(ω) được cho như một hàm của tần số góc ω, do đó mà
| S(ω) = S(f) / 2p | (96) |
và với mô men phổ tương ứng Mn, quan hệ với Mn là:
|
| (97) |
Bảng 4 - Lý thuyết sóng
| Thông số | Lý thuyết sóng Airy | Lý thuyết sóng Stoke bậc 2 | |
| Vùng có độ sâu nước cơ bản | Vùng nước sâu | ||
| Thế vận tốc sóng, θ |
|
|
Cần lưu ý rằng, trong vùng nước sâu, thế vận tốc sóng Stoke bậc 2 tương đương với sóng Airy bậc 1 |
| Vận tốc pha, c |
| gT / (2p) |
|
| Bước sóng λ | cT | gT / (2p) | cT |
| Tung độ mặt sóng ƞ |
|
|
|
| Quỹ đạo phần tử chất lỏng theo phương ngang, x |
|
|
|
| Quỹ đạo phần tử chất lỏng theo phương đứng, z |
|
|
|
| Vận tốc phần tử chất lỏng theo phương ngang, u |
|
|
|
| Vận tốc phần tử chất lỏng theo phương đứng, w |
|
|
|
| Gia tốc phần tử chất lỏng theo phương ngang, |
|
|
|
| Gia tốc phần tử chất lỏng theo phương đứng, |
|
|
|
| Áp suất dưới bề mặt, p |
|
|
|
| Vận tốc nhóm, cg |
|
|
|
| Năng lượng trung bình, E |
|
|
|
| Dòng năng lượng, F | Ecg |
| Ecg |
| Ghi chú: d: độ sâu nước trung bình, g: gia tốc trọng trường, H: chiều cao bụng tới đỉnh sóng k = 2p / λ: số sóng, λ: bước sóng, T: chu kỳ sóng, t: thời gian, x: khoảng cách hướng truyền, z: khoảng cách từ mặt tự do lên trên; ω = 2p / T = tần số góc. Kí hiệu I chỉ ra lý thuyết tuyến tính biên độ nhỏ. | |||
6.5.3 Những thông số trạng thái biển
Những thông số trạng thái biển dưới đây có thể được định nghĩa dưới dạng mô men phổ:
6.5.3.1 Chiều cao sóng đáng kể Hs được cho bởi:
|
| (98) |
6.5.3.2 Chu kỳ cắt không Tz có thể tính bằng:
|
| (99) |
6.5.3.3 Chu kỳ sóng trung bình T1 có thể được tính bằng:
|
| (100) |
6.5.3.4 Chu kỳ đỉnh trung bình Tc có thể được tính bằng:
|
| (101) |
6.5.3.5 Độ dốc sóng đáng kể Ss có thể được tính bằng:
|
| (102) |
6.5.3.6 Một vài thông số có thể được sử dụng để xác định bề rộng phổ:
|
| (103) |
|
| (104) |
|
| (105) |
|
| (106) |
Lưu ý rằng mô men phổ bậc 4 và thông số bề rộng phổ không tồn tại đối với phổ Pierson- Moskowitz và phổ JONSWAP.
6.5.4 Độ dốc sóng
Độ dốc sóng trung bình Ss, Sp và Sl đối với trạng thái biển không điều hòa ngắn hạn được định nghĩa là:
|
| (107) |
|
| (108) |
|
| (109) |
Giá trị giới hạn của Ss có thể, được công nhận bởi các nguồn tin cậy có thể lấy bằng:
| Ss = 1/10 với Tz ≤ 6 s | (110) |
| Ss = 1/15 với Tz ≥ 15 s | (111) |
và được nội suy tuyến tính giữa những giá trị giới hạn. Giá trị giới hạn của Sp có thể lấy bằng:
| Sp = 1/15 với Tz ≤ 8 s | (112) |
| Sp = 1/25 với Tz ≥ 15 s | (113) |
Những giá trị giới hạn thu được từ dữ liệu đo đạc của Norwegian Continental Shelf, nhưng được dự kiến được áp dụng nhiều hơn.
6.5.5 Phổ Pierson-Moskowitz và JONSWAP
6.5.5.1 Phổ Pierson-Moskowitz được cho bởi:
|
| (114) |
Trong đó: ωp = 2p / Tp là tần số góc đỉnh phổ.
6.5.5.2 Phổ JONSWAP SJ(ω) được công thức hóa cải biến từ phổ Pierson-Moskowitz cho điều kiện biển phát triển trong một vị trí có bước sóng giới hạn:
|
| (115) |
Trong đó:
SPM Phổ Pierson-Moskowitz.
γ Thông số hình dạng đỉnh không thứ nguyên.
σ Thông số độ rộng phổ.
σ = σa for ω ≤ ωp
σ = σb for ω > ωp
Aγ = 1-0,287 ln(γ) là một hệ số tiêu chuẩn.
6.5.5.3 Các giá trị trung bình đối với dữ liệu thí nghiệm JONSWAP là γ = 3,3; σa = 0,07; σb = 0,09. Khi γ = 1, phổ JONSWAP trở thành phổ Pierson-Moskowitz.
Phổ JONSWAP là một mô hình hợp lý khi:
|
| (116) |
Trong đó Tp đơn vị là giây và Hs là mét, và nên được sử dụng cùng với lưu ý khi ở bên ngoài khoảng thời gian này. Ảnh hưởng của thông số hình dạng đỉnh γ được thể hiện trong Hình 12.
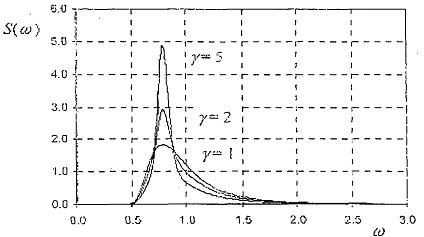
Hình 12 - Phổ JONSWAP đối với Hs = 14,0 m, Tp = 8,0 s đối với γ = 1, γ = 2 và γ = 5
6.5.5.4 Chu kỳ sóng cắt không Tz và chu kỳ sóng trung bình T1 có thể liên quan với chu kỳ đỉnh với phương trình dưới đây (1 ≤ γ < 7).
|
| (117) |
|
| (118) |
Với γ = 3,3; Tp = 1,2859Tz, và T1 = 1,0734T
Với γ = 1,0 (Phổ PM); Tp = 1,4049Tz và T1 = 1,0867Tz
6.5.5.5 Nếu thông số hình dạng đỉnh không có giá trị cụ thể, giá trị dưới đây sẽ được áp dụng:
| γ = 5 khi | (119) |
|
| (120) |
|
| (121) |
Trong đó Tp đơn vị là giây và Hs đơn vị là mét.
6.5.5.6 Đối với phổ JONSWAP, mô men phổ được tính gần đúng là:
|
| (122) |
|
| (123) |
|
| (124) |
|
| (125) |
6.5.5.7 Cả hai phổ JONSWAP và Pierson-Moskowitz đều coi ω-5 là tần số điều chỉnh cao tần (the governing high frequency tail behavior). Đó là số thực nghiệm đối với một hình dạng đồ thị gần với hình dạng lý thuyết. Sự khác nhau giữa ω-4 và ω-5 là tầm quan trọng của phản ứng động kết cấu.
6.5.6 Phổ TMA
Phổ TMA trong vùng có độ sâu nước hữu hạn, không có sóng vỡ, STMA(ω) được xem như phổ JONSWAP nhân với một hàm độ sâu ɸ(ω)
| STMA(ω)=SJ(ω)ɸ(ω) | (126) |
Trong đó:
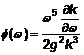
Áp dụng theo quan hệ phân tán:
| ω2 = gk tanh(kd) | (127) |
hàm độ sâu ɸ(ω) có thể viết thành:
|
| (128) |
Trong đó: d là độ sâu nước.
6.5.7 Phổ 2 đỉnh
6.5.7.1 Sự kết hợp gió biển với sóng lừng có thể được miêu tả bởi một phổ tần số 2 đỉnh:
| S(ω) = Swind sea (ω) + sswell (ω) | (129) |
Trong đó gió biến và sóng lừng được giả thiết là không tương quan với nhau.
6.5.7.2 Mô men phổ có tính cộng:
| Mn = Mn,wind sea + Mn,swell | (130) |
từ đó suy ra chiều cao sóng đáng kể được xác định bằng:
|
| (131) |
Trong đó:
Hs,wind sea là chiều cao sóng đáng kể đối với sóng do gió.
Hs,swell là chiều cao sóng đáng kể đối với sóng lừng.
6.5.7.3 Thành phần sóng do gió trong phổ tần số được miêu tả bởi một hàm JONSWAP tổng quát. Thành phần sóng lừng cũng được miêu tả bởi một hàm JONSWAP tổng quát hoặc một hàm tiêu chuẩn.
6.5.7.4 Phổ Ochi-Hubble là một phổ tổng quát được công thức hóa để miêu tả sự kết hợp 2 trạng thái biển khác nhau. Phổ là tổng của hai phân phối Gamma, mỗi phân phối với 3 thông số cho từng hệ thống sóng: Chiều cao sóng đáng kể Hs,j, Chu kỳ đỉnh phổ Tp,j và một hệ số hình dạng λs. Những thông số đó nên được xác định để phù hợp nhất với phổ quan sát.
6.5.7.5 Phổ Ochi-Hubble được định nghĩa là:
|
| (132) |
Trong đó:
![]()
![]()
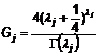
![]()
trong đó: j = 1 và j =2 đại diện lần lượt các yếu tố tần số thấp và cao. Chiều cao sóng đáng kể cho trạng thái biển:
|
| (133) |
6.5.8 Phân phối hướng của gió biển và sóng lừng
6.5.8.1 Phổ hướng sóng đỉnh ngắn có thể được miêu tả theo phổ sóng một chiều:
| S(ω,θ) = S(ω)D(θ,ω) = S(ω)D(θ) | (134) |
Trong đó đẳng thức sau là một đơn giản hóa thường được sử dụng trong thực hành. D(θ, ω) và D(θ) là hàm hướng (directional functions). θ là góc giữa hướng của sóng cơ bản và hướng sóng chính của hệ sóng đỉnh ngắn.
6.5.8.2 Hàm hướng thỏa mãn điều kiện:
|
| (135) |
6.5.8.3 Đối với một phổ 2 đỉnh là một tổng của một yếu tố sóng lừng và một yếu tố gió biển, tổng của phổ tần số hướng S(ω,θ) bằng:
| S(ω,θ) = Swind sea(ω)Dwind sea(θ) + Sswell(ω)Dswell(θ) | (136) |
6.5.8.4 Một hàm hướng thường được sử dụng cho sóng biển là:
|
| (137) |
trong đó Γ là hàm Gamma và |θ - θp| ≤ ![]()
6.5.8.5 Hướng chính θp có thể được điều chỉnh bằng hướng gió nếu dữ liệu hướng sóng không có sẵn.
6.5.8.6 Cần xem xét thích đáng để phản ánh một mối tương quan chính xác giữa trạng thái biển thực tế và hằng số n. Giá trị điển hình cho gió biển là n = 2 đến 4. Nếu sử dụng cho sóng lừng, n > 7 thích hợp hơn.
6.5.8.7 Một công thức thay thế cũng thường dược sử dụng là:
|
| (138) |
Trong đó: |θ - θp| ≤ p
So sánh 2 công thức đối với sự mở rộng hướng, s có thể lấy bằng 2n+1.
Những giá trị điển hình đối với gió biển là s = 5 ~ 15. Nếu sử dụng cho sóng lừng s > 15 là thích hợp hơn.
6.5.8.8 Mở rộng hướng sóng lừng có thể được mô hình hóa bằng một phân phối Poisson:
|
| (139) |
6.5.8 Phân phối ngắn hạn của chiều cao sóng
6.5.9.1 Chiều cao sóng H từ đỉnh đến bụng sóng của một chu kỳ sóng có sự chênh lệch giữa chiều cao đỉnh lớn nhất và chiều cao bụng sóng thấp nhất giữa hai lần sóng cắt không liên tiếp.
6.5.9.2 Chiều cao sóng có thể được mô hình hóa bởi hàm xác suất tích lũy theo phân phối Rayleigh:
|
| (140) |
Trong đó:
![]()
6.5.9.3 Hệ số ρ phản ánh những ảnh hưởng của chiều rộng phổ và giá trị đặc trưng cho ρ nằm trong khoảng -0,75 đến 0,6. Việc giải thích hệ số ρ như một hàm tự tương quan có giá trị bằng một nửa chu kỳ sóng trội nhất, phổ sóng Jonswap với hệ số mở rộng đỉnh 3,3, đưa giá trị ρ = - 0,73. Sự có mặt của sóng lừng cơ bản tạo cho quy trình sóng có biên độ rộng hơn, đến mức làm tăng sự tự tương quan ρ (ρ gần với khoảng -0,65 ~ 0,6).
6.5.9.4 Sự biểu diễn bằng tham số hợp lý của ρ như là hàm của thông số hình dạng đỉnh Jonswap: (1≤γ≤10)
|
| (141) |
6.5.9.5 Một phân phối chiều cao sóng ngắn hạn theo kinh nghiệm là phân phối Weibull:
|
| (142) |
Những thông số tỷ lệ và hình dạng được xác định từ dữ liệu. Những giá trị thông số của phân phối chiều cao sóng Forristall αH = 0,681 và βH = 2,126 cơ bản được dựa trên dữ liệu thu được từ vịnh Mexico.
6.5.10 Phân phối ngắn hạn của đỉnh sóng trên mực nước tĩnh
6.5.10.1 Tung độ mặt sóng phi tuyến có thể được mô hình hóa bởi lý thuyết bậc 2. Phân phối đỉnh Forristal cho đỉnh sóng trên mực nước tĩnh được dựa trên mô phỏng miền thời gian bậc 2:
|
| (143) |
6.5.10.2 Thông số Weibull αc, βc trong phân phối đỉnh Forristall được diễn giải như một hàm của độ dốc S1 và số Ursells Urs:
|
| (144) |
|
| (145) |
Trong đó k1, là số sóng tùy thuộc độ sâu nước hữu hạn phụ thuộc chu kỳ sóng trung bình T1 và d là độ sâu nước. k1 được tìm ra từ quan hệ tán xạ độ sâu nước hữu hạn.
6.5.10.3 Đối với biển đỉnh sóng dài (2D), thông số Weibull được cho bằng:
| αc = 0,3536 + 0,2892S1 + 0,1060Urs | (146) |
|
| (147) |
và với biển đỉnh sóng ngắn (3D):
| αc = 0,3536 + 0,2568S1 + 0,0800Urs | (148) |
|
| (149) |
6.5.10.4 Cần chú ý rằng phân phối Forristall được dựa trên mô phỏng bậc 2. Các điều kiện ở bậc cao hơn có thể gây kết quả lớn hơn không đáng kể chiều cao đỉnh sóng. Do đó giá trị cực hạn được dự đoán bởi phân phối này có khả năng nhỏ hơn về phía thấp.
6.5.10.5 Nếu có thể thực hiện việc đo chiều cao đỉnh sóng tại vị trí cụ thể, những thống kê ngắn hạn cho chiều cao đỉnh sóng có thể được mô hình hóa bởi một trong ba thông số phân phối weibull phù hợp với dữ liệu.
6.5.10.6 Cần chú ý rằng dữ liệu đỉnh sóng từ việc đo đạc sóng sẽ đánh giá không đúng chiều cao của đỉnh sóng lớn nhất.
6.5.10.7 Đối với các số liệu thống kê của chiều cao đỉnh sóng trên mực nước trung bình và triều thiên văn thấp nhất, thống kê nút của đỉnh, độ dâng do bão và triều phải được đưa vào tính toán.
6.5.11 Chiều cao sóng lớn nhất và chiều cao đỉnh lớn nhất trong một trạng thái biển tĩnh
6.5.11.1 Với một trạng thái biển tĩnh có N không phụ thuộc vào độ lớn nhất cục bộ (ví dụ như chiều cao sóng, chiều cao đỉnh, phản ứng) với hàm phân phối F(x), phân phối của độ lớn cực đại được cho bằng FE(x) = F(x)N
6.5.11.2 Giả định 3 thông số Weibull phân phối độ lớn cục bộ:
|
| (150) |
Trong đó γ là thông số cục bộ, α là thông số quy đổi và β là thông số hình dạng
6.5.11.3 Một vài dạng đặc trưng cho giá trị cực đại trong trong trạng thái biển
Bảng 5 - Dạng đặc trưng cho giá trị cực đại xe
| Đại lượng | Giá trị | FE(xe) |
| Dạng (Mode) xc | γ+α.(lnN)1/β | 0,368 N ® ∞ |
| Trung bình xmean |
N lớn | 0,570 N ® ∞ |
| p-phân vị xp |
| p |
| Trung bình Xmedian |
| p = 0,5 |
| Độ lệch chuẩn |
N lớn |
|
xc < xmedian < xmean
6.5.11.4 Dạng (mode) phân phối giá trị cực đại cũng được coi là cực đại lớn nhất đặc trưng và tương ứng với mức vượt 1/ N với phân phối cơ bản, tức là:
| F(xc) = 1 - 1/N | (151) |
Cho FE(xc) = (1 - 1/N)N = 1/e for N ® ∞
Đối với một trạng thái biển dải hẹp, số lớn nhất có thể lấy bằng N = t / Tz trong đó t là khoảng thời gian của trạng thái biển.
6.5.11.5 Chiều cao sóng từ bụng đến đỉnh lớn nhất đặc trưng Hmax trong một trạng thái biển tĩnh với thời gian t có thể lấy bằng:
|
| (152) |
trong đó ρ là thông số bề rộng dải được cho trong 6.5.9.2
6.5.11.6 Giả thiết N không phụ thuộc vào độ lớn nhất, phân phối của giá trị đỉnh cực đại có thể lấy như phân phối Gumbel:
|
| (153) |
Trong đó các thông số của phân phối Gumbel là:
UG = xc = γ + a.(lnN)1/b
![]()
6.5.11.7 Đặc tính hội tụ thu được bằng việc xem xét các số liệu thống kê với một tham biến được thay đổi, ví dụ bằng việc giả định các quá trình bậc 2 Hmax2 hoặc Cmax2 là phân phối Gumble.
6.5.12 Chiều cao và chu kỳ điểm sóng
6.5.12.1 Phân phối xác suất chung ngắn hạn của chiều cao sóng H và chu kỳ sóng T thu được bằng:
| fHT (H,T) = fH(H).fT\H (T\H) | (154) |
6.5.12.2 Phân phối ngắn hạn của T với H cho trước, trong một trạng thái biển với chiều cao sóng đáng kể Hs và chu kỳ sóng T1, có thể được lấy bằng như phân phối chuẩn:
|
| (155) |
Trong đó Ф( ) là hàm phân phối tích lũy Gaussian Tiêu chuẩn được xác định bởi:
|
| (156) |
và
| μT = C1.T1 | (157) |
|
| (158) |
T1 là chu kỳ sóng trung bình. Các hệ số C1 và C2 có thể thay đổi với T1 (hoặc Tz) và phải được xác định từ dữ liệu đo đạc.
6.5.12.3 Nếu thiếu các dữ liệu cụ thể, các kết quả lý thuyết dưới đây có thể được áp dụng cho chu kỳ sóng kết hợp với chiều cao sóng lớn (H > 0,6Hs):
|
| (159) |
|
| (160) |
Trong đó v là bề rộng phổ được định nghĩa trong 6.5.3.
6.5.12.4 Với một trạng thái biển tĩnh, chu kỳ sóng có khả năng nhất của phân phối chuẩn bằng chu kỳ sóng trung bình, không phụ thuộc vào H.
6.5.13 Sóng độc (Freak waves)
6.5.13.1 Sự xuất hiện của những con sóng lớn bất ngờ, được gọi là sóng độc. Mặc dù sự tồn tại của sóng độc thường không được đề cập, nhưng xác suất xuất hiện cũng như đặc tính vật lý của chúng đã được hiểu rõ. Sóng độc được tạo ra bởi các cơ chế: tương tác sóng - dòng chảy, biển kết hợp, tập trung năng lượng sóng.
6.5.13.2 Các định nghĩa khác về sóng độc thường được sử dụng như một đặc trưng cho một chuỗi thời gian 20 phút là Hmax / Hs > 2 (chiều cao từ đỉnh đến bụng sóng lớn nhất) hoặc Cmax / Hs > 1,3 (chiều cao đỉnh lớn nhất), hoặc đồng thời cả hai.
6.6.1 Các chiến lược phân tích
6.6.1.1 Sự thay đổi dài hạn của sóng có thể được miêu tả theo các phân phối chung hoặc theo biểu đồ phân tán để điều chỉnh các thông số trạng thái biển từ dữ liệu có sẵn (HS,Tz, θ) hay (σ, γ, Hs, Tp, θ,).
6.6.1.2 Biểu đồ phân tán đưa ra tần suất xuất hiện của một cặp thông số cho trước như HS,Tz.
Cả phân phối biên và các mô hình môi trường chung có thể được áp dụng cho việc miêu tả sóng. Các mô hình chung thường được lập bằng việc phân phân các phân phối đến dữ liệu sóng từ khu vực thực tế.
6.6.1.3 Hai chiến lược phân tích khác nhau thường được áp dụng là các mô hình tổng thể và mô hình sự kiện:
- Mô hình tổng thể (hoặc phương pháp phân phối ban đầu) dùng tất cả dữ liệu có sẵn từ các chuỗi quan trắc dài liên tục;
- Trong mô hình sự kiện, sự quan trắc trên một số mức ngưỡng được sử dụng (Phương pháp ngưỡng vượt đỉnh Peak Over Threshold (POT) hoặc nguyên lý phân tích bão). Ngoài ra, các cực trị hàng năm hoặc theo mùa cũng được phân tích.
6.6.1.4 Phương pháp phân phối ban đầu (initial distribution method) thường được áp dụng cho phân phối của các thông số trạng thái biển như chiều cao sóng đáng kể. Các phương pháp tiếp cận dựa trên sự kiện có thể được áp dụng cho các thông số trạng thái biển, nhưng cũng có thể được sử dụng trực tiếp cho chiều cao sóng riêng lẻ lớn nhất và chiều cao đỉnh tối đa.
6.6.1.5 Việc lựa chọn nguyên lý là để cân bằng giữa các mô hình trạng thái biển sử dụng tất cả dữ liệu và mô hình sự kiện cực đại dựa trên một tập con các điểm dữ liệu lớn nhất. Trong khi nguyên lý phân phối ban đầu sử dụng nhiều dữ liệu hơn, có sự tương quan giữa các lần quan trắc. Ngược lại, các sự kiện cực đại có tính độc lập hơn, nhưng độ hiếm hoi của chúng lại tăng các thống kê không chắc chắn. Phương pháp sự kiện là các mô hình tham khảo cho các trường hợp thời tiết không biến đổi trong phần lớn thời gian, và có ít các sự kiện có cường độ mạnh.
6.6.1.6 Khi điều chỉnh các phân phối xác suất với dữ liệu, các kỹ thuật điều chỉnh khác có thể được áp dụng, cần chú ý đến phương pháp mô men (MOM), phương pháp bình phương nhỏ nhất (LS) và Ước lượng hợp lý cực đại (MLE).
6.6.1.7 Trong phương pháp mô men (MOM), các thông số phân phối được đánh giá trừ hai hoặc ba mô men thống kê đầu tiên của mẫu dữ liệu. Phương pháp thường đưa ra sự phù hợp với dữ liệu tại mốt của phân bổ. Phương pháp Ước lượng hợp lý cực đại (MLE) có những điểm lợi thế về mặt lý thuyết, nhưng khó trong việc thực hành. Ý tưởng là tối đa hóa một hàm đại diện cho khả năng thu được các số được đo đạc. Trong phương pháp bình phương nhỏ nhất (LS) tổng của bình phương độ lệch giữa phân phối thực nghiệm và xác suất điều chỉnh được giảm thiểu đến mức nhỏ nhất. Phương pháp LS thường chịu ảnh hưởng nhiều hơn của trạng thái cuối hơn phương pháp MOM và MLE.
6.6.1.8 Khi đánh giá độ cực đại, đuôi của phân phối hợp lý nhận dữ liệu và đối với 3 thông số phân phối Weibull, phương pháp bình phương nhỏ nhất LS thường đưa ra đuôi hợp lý hơn phương pháp mô men. Đối với các áp dụng khác, để thích hợp số lượng lớn dữ liệu có thể quan trọng hơn.
6.6.2 Phân phối biên của chiều cao sóng đáng kể
6.6.2.1 Phương pháp phân phối ban đầu: nếu dữ liệu không chỉ ra sự khác biệt, một phân phối 3 thông số Weibull có thể được giả định cho phân phối biên của chiều cao sóng đáng kể Hs
|
| (161) |
Trong đó: α là thông số quy đổi, β là thông số hình dạng và γ là thông số vị trí (ngưỡng thấp). Các thông số phân phối được xác định từ dữ liệu tại vị trí cụ thể bởi kỹ thuật phù hợp.
6.6.2.2 Đối với ngưỡng vượt đỉnh và các phân tích thống kê bão, một phổ 2 thông số Weibull và một phân phối mũ được yêu cầu cho các giá trị vượt mức. Phân phối chung Pareto phải được sử dụng kèm sự lưu ý.
Đối với phân phối mũ:
|
| (162) |
Thông số quy đổi có thể được xác định từ giá trị trung bình của biến dư y = H - h0, tức là θ = E[H - h0]
6.6.2.3 Thống kê vượt ngưỡng đỉnh phải được sử dụng cẩn thận khi các kết quả có thể nhạy với mức ngưỡng được thừa nhận. Phân tích độ nhạy với mức ngưỡng phải được tiến hành. Nếu có thể, thống kê POT phải được so sánh với các kết quả thu được từ các phương pháp thay thế. Phân tích bão được đánh giá cao nếu đủ số lượng sự kiện bão tồn tại. Ngoài ra, các kết quả thống kê bão có thể phụ thuộc vào ngưỡng thấp hơn của các cơn bão, và phải được so sánh với các kết quả thu được từ các phương pháp thay thế.
6.6.2.4 Giá trị cực đại hàng năm của một biến môi trường, như chiều cao sóng đáng kể hoặc chiều cao sóng lớn nhất có thể được giả định theo một phân phối Gumbel:
|
| (163) |
Trong đó A và U là các thông số phân phối tương ứng với độ lệch chuẩn σ = 1,283A và trung bình μ = U + 0,557A của biến Gumbel. Các đánh giá giá trị cực đại phải được so sánh với các kết quả từ các phương pháp thay thế.
6.6.2.5 Nên dựa trên số liệu thống kê hàng năm nhỏ nhất trong 20 năm. Năm được định nghĩa là khoảng chu kỳ từ hè năm này sang hè năm sau (không tính theo lịch năm).
6.6.3 Phân phối chung của chiều cao và chu kỳ sóng đáng kể
6.6.3.1 Các mô hình môi trường chung yêu cầu xử lý tải trọng trong việc phân tích độ tin cậy và đánh giá tầm quan trọng của các biến môi trường khác nhau thay đổi trong các điều kiện tải trọng/phản ứng cực hạn.
6.6.3.2 Tồn tại các phương pháp tiếp cận để thiết lập mô hình môi trường chung. Mô hình hợp lý cực đại (MLM) và phương pháp mô hình hóa theo điều kiện (CMA), sử dụng thông tin xác suất thu được từ việc quan trắc đồng thời từ các biến môi trường. MLM sử dụng việc chuyển đổi Gaussian thành một gói dữ liệu tương thích CMA một hàm mật độ chung được định nghĩa phù hợp với phân phối biên và một chuỗi các hàm mật độ theo điều kiện.
6.6.3.3 Nếu thông tin có sẵn về các biến xảy ra đồng thời bị giới hạn với các phân phối biên và sự tương quan lẫn nhau, mô hình Nataf có thể được sử dụng. Mô hình Nataf phải được sử dụng cẩn trọng do mô hình đơn giản hóa sự phụ thuộc giữa các biến.
6.6.3.4 Mô hình chung CMA khuyến nghị chiều cao sóng đáng kể được mô hình hóa bởi 3 thông số hàm mật độ xác suất Weibull:
|
| (164) |
và chu kỳ sóng cắt không theo điều kiện Hs được mô hình bởi một phân phối lô-ga-rit chuẩn:
|
| (165) |
trong đó các thông số phân phối μ và σ là các hàm của chiều cao sóng đáng kể. Kinh nghiệm chỉ ra rằng các mô hình trên thường đưa ra tính phù hợp cho dữ liệu.
|
| (166) |
|
| (167) |
Các hệ số ai, bi, i = 0,1,2 được xác định từ dữ liệu thực tế.
6.6.4 Phân phối chung của chiều cao sóng đáng kể và tốc độ gió
6.6.4.1 Một phân phối 2 thông số Weibull có thể được áp dụng cho tốc độ gió trung bình U đưa ra trạng thái biển Hs:
|
| (168) |
trong đó thông số quy đổi Uc và thông số hình dạng k được xác định từ dữ liệu thực tế, ví dụ như sử dụng các mô hình:
|
| (169) |
6.6.5 Các hiệu ứng hướng (Directional effects)
6.6.5.1 Đối với gió biển, gió và sóng thường được giả định cùng hướng. Độ chênh lệch hướng giữa sóng và gió θr:
|
| (170) |
có thể được mô hình hóa rõ ràng. Đối với các dữ liệu có tình hướng đồng thời (omnidirectional data), θr có thể giả định là phân phối beta. Phân phối beta là một công cụ linh hoạt để mô hình phân phối của một biến biên, nhưng thường khó áp dụng.
6.6.5.2 Mô hình phân phối của hướng sóng tuyệt đối thường theo xác suất xuất hiện của sóng pθ trong các ống dẫn hướng, và thường được chia các phần thành 8 góc 45 độ, 12 góc 30 độ hoặc 16 góc 22,5 độ. Giá trị ![]() và các thông số sóng cần thiết phải được xác định từ dữ liệu.
và các thông số sóng cần thiết phải được xác định từ dữ liệu.
6.6.5.3 Độ tin cậy đảm bảo cần phải được chấp nhận nếu thông tin về hướng được sử dụng trong phân tích độ tin cậy của kết cấu biển. Nên có sự nhất quán giữa các hướng đều nhau và các phân phối hướng để xác suất vượt ngưỡng bằng xác suất vượt đảm bảo từ tất cả các hướng.
6.6.5.4 Tiêu chí về hướng phải được sử dụng cẩn thận. Nếu đối tượng được định nghĩa là một tập hợp các chiều cao sóng tích lũy vượt quá một chu kỳ lặp 100 năm, chiều cao sóng cho một số phần hoặc toàn bộ phải được tăng lên. Cần lưu ý rằng nếu tiêu chí về hướng được quy đổi sao cho chiều cao sóng ở hướng xấu nhất bằng với giá trị hướng đều nhau, tập hợp sóng sẽ vẫn vượt quá với chu kỳ lặp ít hơn 100 năm.
6.6.5.5 Một tập hợp các chiều cao sóng theo các hướng vượt quá một chu kỳ TR có thể được lập bằng việc yêu cầu kết quả của các xác suất vượt quá từ các phần bằng với mức xác suất thích hợp.
6.6.5.6 Một phương pháp khác phân tích sự thay đổi hướng để mô hình hướng sóng tuyệt đối là sử dụng một phân phối xác suất liên tục.
6.6.6 Thống kê chung của gió biển và sóng lừng
6.6.6.1 Có Hai phương pháp được miêu tả dưới đây. Trong phương pháp đầu, gió biển và sóng lừng được mô hình hóa theo các biến độc lập, là các giả thiết hợp lý liên quan đến vật chất của biển kết hợp. Sử dụng phương pháp này yêu cầu việc áp dụng một phổ sóng được miêu tả đầy đủ bởi các phân phối gió biển và sóng lừng, như phổ JONSWAP. Chiều cao sóng đáng kể bằng:
|
| (171) |
6.6.6.2 Thường khó khăn trong việc thiết lập riêng các phân phối gió biển và sóng lừng và các giả định thừa nhận các phân phối này dẫn đến việc dự đoán không chính xác các giá trị cực đại. Trong vài trường hợp, việc sử dụng phân phối của tổng chiều cao sóng đáng kể và chu kỳ sóng được kết hợp với một phương pháp tách năng lượng sóng giữa gió biển và sóng lừng, như phổ Torsethaugen, được đánh giá cao hơn. Phương pháp này dựa trên các đặc tính gió biển và sóng lừng cho một vị trí cụ thể. Mặc dù vài đặc tính có mức độ nhất định, phương pháp được thành lập sử dụng dữ liệu từ một vị trí xác định phải được sử dụng cẩn thận khi áp dụng cho các khu vực biển khác.
6.6.7 Phân phối dài hạn của chiều cao sóng đơn
Phân phối dài hạn FH(x) của chiều cao sóng đơn có thể thu được bằng tích phân phân phối ngắn hạn
![]() trên tất cả trạng thái biển, hiệu chỉnh (weighting) cho số các chu trình sóng đơn với từng trạng thái biển.
trên tất cả trạng thái biển, hiệu chỉnh (weighting) cho số các chu trình sóng đơn với từng trạng thái biển.
|
| (172) |
Trong đó:
![]()
![]()
Chiều cao sóng đơn ![]() với chu kỳ lặp TR (theo năm):
với chu kỳ lặp TR (theo năm):
|
| (173) |
6.7.1 Trạng thái biển thiết kế
6.7.1.1 Khi ![]() thể hiện phân phối của chiều cao sóng đáng kể trong một trạng thái biển bất kỳ, phân phối của chiều cao sóng đáng kể lớn nhất hàng năm Hs,max có thể lấy bằng:
thể hiện phân phối của chiều cao sóng đáng kể trong một trạng thái biển bất kỳ, phân phối của chiều cao sóng đáng kể lớn nhất hàng năm Hs,max có thể lấy bằng:
|
| (174) |
Trong đó n là số trạng thái biển trong một năm. Khi t = 3, n = 2922. Đối với bão, ![]() thể hiện phân phối của chiều cao sóng đáng kể lớn nhất trong bão, và n phụ thuộc vào số cơn bão trong một năm.
thể hiện phân phối của chiều cao sóng đáng kể lớn nhất trong bão, và n phụ thuộc vào số cơn bão trong một năm.
6.7.1.2 Chiều cao sóng đáng kể với chu kỳ lặp theo năm TR có thể được định nghĩa là phân vị (1-1/(nTR)) của phân phối chiều cao sóng đáng kể, trong đó n là số trạng thái biển một năm, được ký hiệu ![]() và có công thức:
và có công thức:
|
| (175) |
6.7.1.3 Ngoài ra, ![]() có thể được định nghĩa như là phân vị (1-1/TR) trong phân phối của chiều cao sóng đáng kể hàng năm lớn nhất, như xác xuất vượt trong một năm của chiều cao sóng đáng kể là 1/TR
có thể được định nghĩa như là phân vị (1-1/TR) trong phân phối của chiều cao sóng đáng kể hàng năm lớn nhất, như xác xuất vượt trong một năm của chiều cao sóng đáng kể là 1/TR
|
| (176) |
Một chu kỳ lặp TR cho trạng thái biển thiết kế có khoảng thời gian từ 3-6 giờ, với chiều cao sóng đáng kể ![]() được kết hợp với các giá trị đặc trưng được chọn thích hợp với các thông số trạng thái biển khác. Ví dụ các giá trị Tp hoặc Tz thường thay đổi theo một giá trị thời gian trung bình. Phương pháp này được lập bằng việc xem xét các đường biên môi trường (environmental contours) được miêu tả trong mục tiếp theo.
được kết hợp với các giá trị đặc trưng được chọn thích hợp với các thông số trạng thái biển khác. Ví dụ các giá trị Tp hoặc Tz thường thay đổi theo một giá trị thời gian trung bình. Phương pháp này được lập bằng việc xem xét các đường biên môi trường (environmental contours) được miêu tả trong mục tiếp theo.
6.7.1.4 Giá trị gần đúng của trạng thái biển thiết kế giả định phản ứng cực đại n -năm có thể được ước lượng từ điều kiện chiều cao sóng đáng kể lớn nhất n-năm. Giá trị này yêu cầu vài phương pháp tính toán các biến phản ứng ngắn hạn của trạng thái biển, như sự tăng chiều cao sóng đáng kể hoặc sử dụng một giá trị phân vị cho phân phối giá trị cực đại ngắn hạn của phản ứng.
6.7.2 Đường biên môi trường
6.7.2.1 Đường biên môi trường thể hiện một quy trình hợp lý để xác định điều kiện trạng thái biển cực hạn. Để xác định đường biên từ các thông số môi trường (thường là Hs,Tp) theo các phản ứng cực đại với giá trị chu kỳ lặp cho trước có thể được chấp nhận.
6.7.2.2 Phương pháp IFORM
- Xác định mô hình môi trường chung của các biến trạng thái biển:
| Với Hs, Tz: | (177) |
- Biến đổi phân phối sang khoảng U Tiêu chuẩn:
|
| (178) |
- Lập các phạm vi của chu kỳ lặp trong khoảng U. Với các quan trắc được ghi lại mỗi 3 giờ, bán kính cho đường biên 100 năm là:
|
| (179) |
- Biến đổi chu vi của một đường biên trong khoảng thông số môi trường:
|
|
| (180) |
6.7.2.3 Phương pháp mật độ xác suất không đổi (constant probability density approach).
- Xác định mô hình môi trường chung của các biến trạng thái biển:
| Với Hs, Tz: | (181) |
- Đánh giá giá trị cực đại của các biến điều chỉnh với chu kỳ lặp định mức, và các giá trị tương ứng cho các biến khác. Ví dụ với giá trị 100 năm của Hs và giá trị trung bình có điều kiện của Tz
- Đường biên được lập từ mô hình chung hoặc sơ đồ phân tán khi đường biên của mật độ xác suất không đổi đi qua thông số kết hợp được đề cập bên trên.
6.7.2.4 Đánh giá phản ứng cực đại thu được từ việc tìm theo đường biên môi trường theo điều kiện đưa ra phản ứng cực đại đặc trưng lớn nhất.
6.7.2.5 Phương pháp này có khuynh hướng đánh giá thấp mức độ phản ứng cực đại vì nó bỏ qua các biến phản ứng do trạng thái biển ngắn hạn khác nhau. Biến ngắn hạn có thể được tính theo các cách khác nhau.
6.7.2.6 Có thể đánh giá gián tiếp và gần đúng khi đưa vào tính phản ứng cực đại bằng việc tăng chu kỳ lặp và các đường biên môi trường.
6.7.2.7 Tăng phản ứng: Có thể thay phản ứng ngẫu nhiên bởi một mức phân vị cố định cao hơn giá trị trung bình hoặc nhân tử của trung bình phản ứng cực đại.
6.7.2.8 Mức phân vị thích hợp và nhân tử sẽ là trường hợp cụ thể và phải được xác định cấp và phản ứng của kết cấu. Thông thường, Hệ số và phân vị thích hợp sẽ lớn hơn đối với các trường hợp phi tuyến. Các giá trị được ghi lại là các phân vị từ 75% đến 90% đối với phản ứng 100 năm và nhân với hệ số từ 1,1 đến 1,3.
6.7.3 Chiều cao sóng đơn cực đại và chiều cao đỉnh cực đại
6.7.3.1 Chiều cao sóng đơn lớn nhất trong trạng thái biển bất kỳ có công thức:
|
| (182) |
Trong đó:
![]() là mật độ xác suất chung cho HS và TZ (mặt khác Tp hoặc T1 có thể được sử dụng);
là mật độ xác suất chung cho HS và TZ (mặt khác Tp hoặc T1 có thể được sử dụng);
![]() là phân phối của chiều cao sóng lớn nhất với các thông số HS,TZ. Một công thức tương ứng áp dụng cho chiều cao đỉnh sóng và cho các cơn bão.
là phân phối của chiều cao sóng lớn nhất với các thông số HS,TZ. Một công thức tương ứng áp dụng cho chiều cao đỉnh sóng và cho các cơn bão.
6.7.3.2 Công thức dưới đây được yêu cầu để thành lập phân phối của các cơn sóng cực đại dựa trên các thống kê bão:
- Lập phân phối của chiều cao sóng lớn nhất trong bão, phù hợp một phân phối Gumbel với hmax2, xác định hmax,m và phương sai cho phân phối giá trị cực đại trong từng cơn bão;
- Tiến hành phân tích POT cho từng trường hợp (modes);
- Lập phân phối cho chiều cao sóng lớn nhất trong một cơn bão bất kỳ.
|
| (183) |
Thông số ln(N) là một hàm của hệ số phương sai của hmax2, giá trị đặc trưng cho bão tại vùng biển Bắc ln(N) = 8. Công thức tương tự áp dụng cho chiều cao đỉnh sóng lớn nhất.
6.7.3.3 Phân phối giá trị cực đại hàng năm của chiều cao sóng thu được bằng việc tích phân các thống kê ngắn hạn:
|
| (184) |
Trong đó: n là số sự kiện trong năm (trạng thái biển hoặc bão). Công thức áp dụng cho chiều cao đỉnh sóng.
6.7.3.4 Việc giả định trạng thái biển theo 3 giờ, giá trị ![]() với chu kỳ lặp (trong năm) TR:
với chu kỳ lặp (trong năm) TR:
|
| (185) |
Chiều cao sóng có thể được biểu thị như phân vị 1/TR cho phân phối của chiều cao sóng lớn nhất hàng năm:
|
| (186) |
Ví dụ chiều cao sóng đơn 100 năm H100 phụ thuộc vào chiều cao sóng với xác suất vượt hàng năm 10-2
Trong 6.5.11 phân phối của chiều cao sóng lớn nhất hàng năm hoặc chiều cao đỉnh sóng lớn nhất hàng năm có thể được giả định theo một phân phối Gumbel.
6.7.3.5 Nếu thiếu thông tin chi tiết, đối với các trạng thái biển có thời lượng 3 giờ, H100 có thể lấy bằng 1,9 lần chiều cao sóng đáng kể Hs,100.
6.7.4 Chu kỳ sóng của chiều cao sóng đơn cực đại
6.7.4.1 Chu kỳ sóng đơn THmax được sử dụng kết hợp với chiều cao sóng cực đại dài hạn Hmax, có công thức như sau:
|
| (187) |
Trong đó a và b là hệ số thực nghiệm.
6.7.4.2 Chu kỳ THmax được sử dụng kết hợp với H100 phải nằm trong khoảng:
|
| (188) |
6.7.5 Sự tiến triển của bão
Trong việc đánh giá sức kháng của móng chống lại tải trọng sóng lặp lại, sự tiến triển của bão phải được đưa vào tính toán. Điều này phải bao quát đầy đủ sự phát triển và suy yếu của cơn bão.
Nếu dữ liệu tại vị trí cụ thể không có sẵn, profile bão trong Hình 13 có thể được áp dụng:
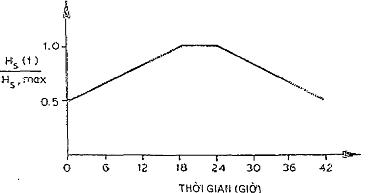
Hình 13 - Chiều cao sóng đáng kể tương ứng với giá trị lớn nhất
7 Điều kiện dòng chảy và triều
7.1.1 Quy định chung
7.1.1.1 Ảnh hưởng của dòng chảy phải được xem xét trong thiết kế kết cấu công trình biển, cũng như trong quá trình chế tạo và khai thác.
7.1.1.2 Những mục dưới đây phải được xem xét trong việc thiết kế kết cấu công trình biển:
- Dòng chảy có thể gây ra sự lệch trục lớn và chuyển động trôi chậm lên các giàn neo;
- Dòng chảy gây gia tăng các lực cản và lực nâng lên kết cấu chìm;
- Dòng chảy có thể gây ra tăng dao động gây do xoáy nước của các phần tử kết cấu mảnh và các chuyển động gây ra do xoáy của kết cấu có thể tích lớn;
- Sự tương tác giữa dòng chảy mạnh và sóng dẫn đến những thay đổi trong chiều cao và chu kỳ sóng;
- Dòng chảy có thể tạo ra những vết xói dưới đáy biển xung quanh vị trí kết cấu được lắp đặt.
7.1.1.3 Phân phối thống kê và profile vận tốc của dòng chảy thường ít đối với hầu hết các khu vực trên thế giới. Những giai đoạn đo đạc dòng chảy được khuyến nghị trong giai đoạn đầu phát triển khai thác dầu khí ngoài khơi. Việc đo đạc tại vị trí thi công nên được mở rộng trên toàn cột nước và trên toàn chu kỳ thu được trong các cơn bão lớn.
7.1.1.4 Nếu có đủ dữ liệu sóng - dòng chảy, phân phối chung của những thông số và đường cong hoặc mặt phẳng biên liên quan tới xác suất vượt quá có thể được lập ra.
7.1.2 Các loại dòng chảy
7.1.2.1 Các dòng chảy phổ biến:
- Dòng chảy do gió;
- Dòng chảy do thủy triều;
- Dòng chảy tuần hoàn;
- Dòng chảy lặp và xoáy (loop/eddy current);
- Dòng chảy Soliton;
- Dòng chảy dọc bờ.
7.1.2.2 Dòng chảy do gió tạo ra bởi sự chênh lệch áp lực gió và áp suất không khí suốt một cơn bão.
7.1.2.3 Dòng chảy do thủy triều diễn ra đều đặn theo sự thay đổi thiên văn của trái đất. Dòng chảy triều lớn nhất đạt được hoặc cùng triều thiên văn cao hoặc thấp nhất. Dòng chảy triều thường yếu trong vùng nước sâu, nhưng lại được gia tăng ở các khu vực đường bờ biển. Dòng chảy triều mạnh tồn tại trong các khu vực vịnh và dọc theo bờ biển.
7.1.2.4 Dòng chảy tuần hoàn là dòng chảy tĩnh, có quy mô lớn của sự tuần hòa biển nói chung. Các phần của dòng chảy tuần hoàn có thể tách từ dòng tuần hoàn chính thành những xoáy có kích thước lớn. Vận tốc dòng chảy trong những xoáy đó có thể vượt quá vận tốc của dòng chảy tuần hoàn chính.
7.1.2.5 Dòng chảy soliton tạo ra bởi những con sóng liên tiếp do sự chênh lệch mật độ.
7.1.2.6 Dòng chảy lặp và xoáy (loop/eddy current) và dòng chảy soliton xuyên sâu trong cột nước.
7.1.2.7 Dòng chảy dọc bờ chạy song song với đường bờ trong vùng bờ biển như kết quả của sóng vỡ tại một góc trên bờ.
7.1.2.8 Động đất có thể là lý do làm lớp trầm tích mất ổn định và thiết lập dòng chảy theo trọng lực. Những dòng chảy này được gọi là dòng chảy rối. Trầm tích trong dòng chảy cho mật độ cao hơn nước môi trường. Các dòng chảy này phải được đưa vào tính toán trong thiết kế đường ống đi qua sườn lục địa có trầm tích không ổn định. Động đất mạnh dưới nước có thể tạo ra sóng thần (tsunami) ở vùng ven bờ.
7.1.3 Vận tốc dòng chảy
7.1.3.1 Véc tơ vận tốc dòng chảy thay đổi theo độ sâu nước. Gần với bề mặt nước, profile vận tốc dòng chảy được kéo dài hoặc nén do sóng bề mặt (xem Hình 14). Về cơ bản, véc tơ vận tốc thay đổi theo không gian và thời gian:
| vc = vc(x,y,z,t) | (189) |
Sự phụ thuộc thời gian là do dao động dòng chảy gây ra bởi sự nhiễu loạn.
7.1.3.2 Trong hầu hết các áp dụng, vận tốc dòng chảy có thể được xem xét như một khu vực dòng chảy đều có véc tơ vận tốc chỉ là một hàm của độ sâu. Việc thiết kế các kết cấu nhạy với dòng chảy động nên kể đến ảnh hưởng của các rối loạn.
7.1.3.3 Tổng vận tốc dòng chảy tại tọa độ cho trước phải được lấy như véc tơ tổng của từng từng thành phần đại diện cho dòng chảy như dòng chảy do gió, triều và dòng chảy tuần hoàn:
| vc(z) = vc,wind(z) + vc,tide(z) + vc,circ(z) + … | (190) |
7.1.4 Profile dòng chảy thiết kế
7.1.4.1 Khi việc đo đạc chi tiết không được thực hiện, tham số trong vùng nước nông của vận tốc dòng chảy do thủy triều có thể được mô hình hóa như một luật lũy thừa đơn giản, giả định như dòng chảy đơn hướng:
|
| (191) |
7.1.4.2 Sự biến đổi của dòng chảy do gió có thể được lấy như một profile tuyến tính từ z = -d0 đến mực nước tĩnh:
|
| (192) |
Hoặc một profile dạng:
| vc,wind(z) = vc,wind(0) khi -d0 < z < 0 | (193) |
Profile cho các tải trọng lớn nhất phải được áp dụng.
7.1.4.3 Dòng chảy do gió có thể được giả định bằng 0 tại một khoảng cách dưới mực nước tĩnh:
| vc,wind(z) = 0 khi z < -d0 | (194) |
Trong đó:
vc(z) Tổng vận tốc dòng chảy tại cao độ z;
z Khoảng cách từ mực nước tĩnh;
vv,tide(0) Vận tốc dòng chảy do triều tại mực nước tĩnh;
vc,wind(0) Vận tốc dòng chảy do gió tại mực nước tĩnh;
d Độ sâu nước đến mực nước tĩnh (giá trị dương);
d0 Độ sâu tham chiếu cho dòng chảy do gió, d0 = 50 m;
α Số mũ - thông thường lấy α = 1/7.
7.1.4.4 Tại vùng nước sâu dọc theo một đường bờ biển mở, nếu dữ liệu thống kê không có sẵn, vận tốc dòng chảy do gió tại mực nước tĩnh có thể được lấy như sau:
| vc,wind(0) = kU1hour,10m trong đó k = 0,015 đến 0,03 | (195) |
U1hour,10m là tốc độ gió duy trì trong 1 giờ tại độ cao 10 m trên mực nước biển.
7.1.4.5 Sự thay đổi của vận tốc dòng chảy theo độ sâu phụ thuộc vào thời tiết biển của địa phương, phân phối mật độ theo phương đứng và dòng chảy nước trong hoặc bên ngoài khu vực. Nó có thể thay đổi từ mùa này sang mùa khác. Profile độ sâu nước là phức tạp. Hướng của dòng chảy có thể thay đổi 180 độ theo độ sâu.
7.1.4.6 Khi dữ liệu đo profile dòng chảy dài hạn có sẵn, profile dòng chảy thiết kế có thể nhận được bằng thông số hóa dữ liệu sử dụng những hàm trực giao thực nghiệm (EOF). Phương pháp kỹ thuật này được sử dụng cho việc thay thế một tập hợp các chuỗi phân phối thời gian theo không gian như là một tổng các hàm không gian trực giao bm (EOFs) nhân với biên độ thời gian wm (t). Profile dòng chảy tại tọa độ x có thể biểu diễn bằng:
|
| (196) |
7.1.4.7 Những profile với chu kỳ lặp có thể được chọn bằng việc áp dụng EOFs và nghịch đảo lý thuyết độ tin cậy bậc 1 IFORM.
7.1.4.8 Trong khi phổ năng lượng tần số được sử dụng rộng rãi cho tải trọng sóng (gần với bề mặt sóng) và cho tải gió (gần với mặt đất hoặc mặt biển), thì cơ bản không hữu dụng với tải trọng dòng chảy ngoài việc nằm trong lớp mất ổn định gần với đáy biển (như đường ống biển). Các điều kiện dòng chảy gần đáy biển được nêu trong TCVN 6475:2017.
7.1.5 Sự mở rộng của dòng chảy đến mặt sóng
7.1.5.1 Sự thay đổi trong profile dòng chảy với độ sâu nước khác nhau tùy thuộc hoạt động của sóng phải được xem xét. Trong những trường hợp như vậy profile dòng chảy có thể được mở rộng hoặc nén lại theo phương đứng, nhưng vận tốc dòng chảy tại mọi tương quan của độ sâu nước tức thời là không đổi, xem Hình 14. Bằng nguyên lý này, dòng chảy mặt vẫn không đổi.
7.1.5.2 Sự mở rộng được biểu diễn bằng việc đưa vào một tọa độ đứng mở rộng zs để tốc độ dòng chảy v(z) tại độ sâu z trong profile nước tĩnh vẫn nằm tại tọa độ mở rộng zs.
7.1.5.3 Sự mở rộng tuyến tính được định nghĩa bời:
| zs = (d+ƞ)(1+z/d)-d; -d ≤ zs ≤ ƞ | (197) |
Trong đó: ƞ là đường mặt nước và d là độ sâu nước tĩnh. Điều này là quan trọng như sự mở rộng Wheeler được sử dụng cho động học sóng trên tọa độ z = 0 đối với sóng tuyến tính.
7.1.5.4 Mở rộng phi tuyến được xác định bằng liên hệ zs và z thông qua lý thuyết sóng tuyến tính Airy:
|
| (198) |
Trong đó knl là số sóng phi tuyến phụ thuộc bước sóng λnl đối với sóng đều được xem xét cho độ sâu nước d và chiều cao sóng H. Mở rộng phi tuyến đưa ra sự mở rộng lớn nhất tại mặt biển mà tại đó chuyển động quỹ đạo sóng có bán kính lớn nhất.
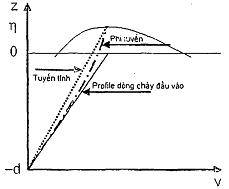
Hình 14 - Sự mở rộng phi tuyến đưa ra sự mở rộng lớn nhất tại mặt biển
7.1.5.5 Trong phần lớn trường hợp, sự mở rộng tuyến tính đưa ra các ước lượng chính xác về tải trọng thủy động tổng thể. Tuy nhiên, nếu profile dòng chảy có tốc độ rất cao tại bề mặt, với một lực cắt lớn dưới bề mặt, mở rộng phi tuyến phải được sử dụng.
7.1.5.6 Nếu dòng chảy không cùng hướng với hướng sóng, cả hai yếu tố theo dòng và vuông góc với dòng chảy có thể được mở rộng. Đối với sóng không đều, lý thuyết mở rộng áp dụng với từng đỉnh-bụng sóng riêng biệt.
7.1.6 Mô phỏng số học của dòng chảy
Mô hình số học tin cậy có thể được sử dụng để dự đoán vùng dòng chảy tại các vị trí không thể đo đạc. Đầu vào của các mô hình là việc đo đạc tại một lượng hữu hạn các địa điểm hoặc sự quan sát từ vệ tinh.
Những mô hình số học đại dương (Numerical ocean models) phải được sử dụng cẩn thận. Những mô hình này phải được xác nhận sự phù hợp bằng việc đo đạc trước khi được sử dụng một cách tin cậy nhất.
7.1.7 Đo đạc dòng chảy
7.1.7.1 Có hai dạng đo dạc khác nhau để thu thập thông tin về vận tốc dòng chảy:
- Đo đạc trực tiếp đưa ra thông tin về vận tốc dòng chảy tại một số hữu hạn các điểm cố định. Mẫu thử được lấy từ những thiết bị đo dòng chảy, phát ra một loạt các xung sóng âm ngắn, sau đó đo tín hiệu phản xạ lại từ các hạt di chuyển với dòng chảy;
- Đo đạc gián tiếp qua độ mặn và nhiệt độ tại một số lượng các vị trí được sử dụng để ước lượng mật độ và vận tốc dòng chảy trung bình có thể thu được từ phương trình phát sinh từ hiện tượng trái đất quay.
7.1.7.2 Để xác định vận tốc dòng chảy trung bình trong dòng chảy tuần hoàn, dòng chảy lặp và xoáy và dòng chảy triều, chu kỳ trung bình 10 phút hoặc dài hơn được sử dụng khi ghi lại vận tốc dòng chảy. Để giải quyết sự thay đổi về tỷ lệ chia thời gian tương ứng với chu kỳ phản ứng động của kết cấu biển, các chu kỳ trung bình ngắn cần được quan tâm.
7.2.1 Độ sâu nước
7.2.1.1 Độ sâu nước tại mọi vị trí ngoài khơi bao gồm một thành phần cố định và một thành phần thay đổi theo thời gian. Những sự thay đổi đó gây ra do triều thiên văn, do gió và áp lực không khí. Gió và những sự thay đổi áp suất khí quyển gây lên độ nước dâng do bão. Những yếu tố ảnh hưởng tới sự thay đổi độ sâu nước có thể do những thay đổi thời tiết dài hạn, sự rút xuống mặt biển hoặc sự tăng từng đoạn của mực nước như sóng thần.
7.2.1.2 Sự xác định tốt nhất độ sâu nước và sự thay đổi của nó được đưa ra từ việc đo đạc tại vị trí cụ thể với thiết bị đo áp lực tại mặt đáy biển. Sự xác định chính xác của thủy triều cực đại, bao gồm triều thiên văn cao nhất (HAT) và triều thiên văn thấp nhất (LAT) theo số liệu đo đạc được thực hiện ít nhất 1 năm.
7.2.1.3 Khi nhận được dữ liệu đo đạc mực nước, cần phải kiểm tra độ dâng thủy triều đã được loại bỏ hay không. Điều này là quan trọng để có thể lập một mô hình nước dâng.
7.2.2 Các mực thủy triều
7.2.2.1 Khoảng triều được định nghĩa là khoảng chênh lệch giữa mức triều thiên văn cao nhất HAT và triều thiên văn thấp nhất LAT (Hình 15)
7.2.2.2 HAT là mức cao nhất và LAT là mức thấp nhất có thể xảy ra dưới các điều kiện khí tượng học trung bình và dưới bất kỳ sự kết hợp của các điều kiện thiên văn.
7.2.2.3 Giá trị của LAT và HAT được xác định bằng việc khảo sát với một khoảng nhiều hơn một năm.
7.2.2.4 Triều cường (spring tides) là thủy triều có biên độ được gia tăng xảy ra gần thời điểm trăng rằm và trăng mới. Lực hấp dẫn của mặt trăng và mặt trời tác động làm gia tăng lẫn nhau.
7.2.2.5 Triều rút (neap tides) là thủy triều có biên độ bị giảm xảy ra gần thời điểm đầu và ¾ chu kỳ trăng. Lực hấp dẫn của mặt trăng và mặt trời làm giảm lẫn nhau.
7.2.2.6 Chiều cao của triều cường cao trung bình (MHWS) là trung bình chiều cao của hai con nước cao liên tiếp trong khoảng thời gian 24 giờ (khoảng 1 lần hai tuần) khi biên độ triều là lớn nhất. Chiều cao của triều cường thấp trung bình (MLWS) là trung bình chiều cao thu được bằng 2 con nước thấp liên tiếp trong cùng chu kỳ.
7.2.2.7 Chiều cao của triều rút cao trung bình (MHWN) là trung bình của chiều cao của 2 con nước liên tiếp trong suốt chu kỳ (khoảng 1 lần hai tuần) khi vùng triều là thấp nhất. Chiều cao của của triều rút thấp trung bình (MLWN) là trung bình chiều cao thu được từ 2 con nước thấp liên tiếp trong cùng chu kỳ.
7.2.2.8 Các giá trị của MHWS, MLWS, MHWN và MLWN thay đổi từ năm này qua năm khác với chu kỳ khoảng 18,6 năm. Nói chung, các mực nước được tính toán từ ít nhất một năm và được quyết định cho các thay đổi chu kỳ dài cho giá trị trung bình trên toàn chu kỳ.
7.2.3 Mực nước tĩnh trung bình
Mực nước tĩnh trung bình (MWL) được định nghĩa là mực nước trung bình giữa HAT và LAT, xem Hình 15.
7.2.4 Mực nước dâng do bão
Mực nước dâng do bão bao gồm ảnh hưởng gây ra do gió và áp suất. Để có số liệu chính xác mực nước dâng do bão cần yêu cầu việc đo đạc dài hạn trên 10 năm. Quan hệ giữa mực nước dâng do bão và chiều cao sóng đáng kể được thành lập bởi một mô hình hồi quy. Mực nước rút do bão có tầm quan trọng với hoạt động định hướng gần bờ và cảng, đặc biệt trong vùng nước nông.
7.2.5 Mực nước tĩnh lớn nhất
Mực nước tĩnh lớn (hoặc cao nhất) (SWL) được định nghĩa là triều thiên văn cao nhất tính cả mực nước dâng do bão, xem Hình 15. Mực nước tĩnh thấp nhất được định nghĩa là triều thiên văn thấp nhất không bao gồm mực rút nước do bão.
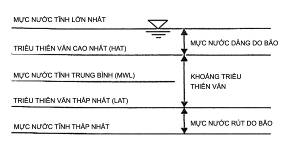
Hình 15 - Các định nghĩa về mực nước
Tải trọng do gió lên kết cấu nói chung là tải trọng phụ thuộc vào thời gian do sự thay đổi của vận tốc gió. Tải trọng gió tác dụng lên mặt ngoài của kết cấu và có thể tác dụng lên phần mặt phẳng bên trong của các kết cấu mở. Áp lực gió tác động lên một phương vuông góc với bề mặt. Khi một mặt phẳng lớn bị gió quét qua, lực ma sát do sự cản tiếp tuyến (due to tangential drag) cũng phải được xem xét.
Phản ứng của một kết cấu do tải trọng gió là một sự cộng tác động của phản ứng tĩnh và phản ứng cộng hưởng do sự kích thích gần với các tần số tự nhiên.
Các ảnh hưởng động có thể là:
- Phản ứng cộng hưởng hóa do sự rối loạn gió (xem 8.6);
- Phản ứng do xoáy;
- Galloping / flutter.
Do tốc độ gió thay đổi theo độ cao, chiều cao của kết cấu hoặc cấu kiện xem xét sẽ được đưa vào. Xem thêm trong 5.3.2.
Tải trọng gió tổng thể lên kết cấu được xác định khi sử dụng một tốc độ thiết kế theo thời gian trung bình trong một mẫu tốc độ gió duy trì. Để thiết kế các thành phần riêng lẻ, tốc độ gió theo thời gian trung bình cũng phải phù hợp, nhưng phải được rút gọn để tính đến tỷ lệ chảy rối nhỏ hơn.
Đối với thiết kế kết cấu giàn có tính đến phản ứng động, sự thay đổi của thời gian và không gian của tốc độ gió cần được kể đến. Khi trường gió chứa năng lượng tại tần số gần tần số dao động tự nhiên của kết cấu, việc phân tích động sử dụng phổ tần số gió nên được tiến hành.
8.2.1 Khái niệm áp lực gió
Áp lực gió cơ sở được định nghĩa bằng phương trình dưới đây:
|
| (199) |
Trong đó:
q Áp lực gió cơ sở;
ρa Trọng lượng riêng của không khí, lấy bằng 1226 kg/ m3 đối với khí khô tại 150°C;
UT,z U(T,z) = Vận tốc gió trung bình trong 1 khoảng thời gian liên tục T tại độ cao z trên mực nước tĩnh hoặc trên mặt đất.
8.2.2 Hệ số áp lực gió
Các mặt phẳng đứng hoặc ngăng bên ngoài của kết cấu kín, không bị che chắn hoàn toàn, phải được kiểm tra áp lực gió cục bộ sử dụng công thức dưới đây:
| p = ±Cpq | (200) |
Trong đó:
p Áp lực hoặc lực hút gió;
q Áp lực hoặc lực hút gió cơ sở;
Cp Hệ số áp lực.
Hệ số áp lực có thể chọn bằng 1,0 cho mặt phẳng ngang và đứng.
8.3.1 Lực gió - Quy định chung
Lực gió Fw lên một phần tử kết cấu và mặt phẳng vuông góc với trục phần tử hoặc mặt phẳng có thể được tính toán theo:
| Fw = CqS sinα | (201) |
Trong đó:
C Hệ số hình dạng;
q Áp lực hoặc lực hút gió;
S Diện tích được chiếu của phân tử vuông góc với hướng của lực;
α Góc giữa hướng của gió và trục của phần tử hoặc mặt phẳng.
Hướng gió bất lợi nhất trên mặt ngang nên được sử dụng khi tính toán độ bền phần tử chịu tác động của gió. Sự tương quan không gian của gió có thể được đưa vào xem xét đối với những mặt phẳng lớn. Áp lực gió cục bộ có thể quan trọng trong việc thiết kế các panel bên ngoài trên thượng tầng. Áp lực do lực nâng của gió lên kết cấu có thể là một vấn đề thiết kế quan trọng.
8.3.2 Ảnh hưởng rắn (Solidification effect)
Nếu một vài phần tử có vị trí trong một mặt vuông góc với hướng gió, như trong trường hợp một dàn phẳng hoặc một dãy cột, ảnh hưởng rắn ϕ phải được đưa vào tính toán. Lực gió:
| FW,SOL = CeqSϕsinα | (202) |
Trong đó:
Ce Hệ số ảnh hưởng hình dạng;
q Áp lực gió cơ sở;
S Được lấy như phần diện tích được chiếu giới hạn bởi dầm;
ϕ Hệ số rắn (solidity ratio) được định nghĩa như phần diện tích nhô ra của dầm vuông góc với hướng của lực bị chia bởi vùng quanh biên của dầm vuông góc với hướng của lực;
α Góc giữa hướng gió và trục của phần tử.
8.3.3 Hiệu ứng chắn
Nếu hai hoặc các dằm song song có vị trí sau hướng gió, hiệu ứng chắn sẽ được đưa vào tính toán. Lực gió lên dằm bị chắn được tính như sau (nếu phương trình trong 5.3.1 được áp dụng):
| FW, SHI = FWƞ | (203) |
hoặc (nếu phương trình trong 5.3.2 Được áp dụng):
| FW, SHI = FW,SOLƞ | (204) |
Trong đó: ƞ là hệ số chắn.
Hệ số chắn phụ thuộc vào tỷ số rắn của khung hướng gió, loại phần tử bao gồm khung và tỷ số khoảng cách của khung. Hệ số chắn có thể được chọn theo Bảng 6.
Nếu có hơn hai phần tử hoặc khung có vị trí nằm theo hướng gió, tải trọng gió lên phần còn lại của phần tử hoặc khung phải được đưa vào bằng tải trọng gió lên phần tử hoặc dầm thứ hai.
8.4.1 Trụ tròn
Hệ số hình dạng đối với trụ tròn có chiều dài hữu hạn có thể được chọn theo Hình 22. Số Reynolds được định nghĩa như sau:
|
| (205) |
Trong đó:
D Đường kính của phần tử;
UT,z Vận tốc gió trung bình;
va Độ nhớt động học của không khí, có thể lấy bằng 1,45x10-5 m2/s tại 15°C và áp suất không khí tiêu chuẩn.
Bảng 6 - Hệ số chắn ƞ là hàm của tỉ số khoảng cách α và tỷ số rắn khí động học β
| β | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 |
| <1,0 | 1,0 | 0,96 | 0,90 | 0,80 | 0,68 | 0,54 | 0,44 | 0,37 |
| 2,0 | 1,0 | 0,97 | 0,91 | 0,82 | 0,71 | 0,58 | 0,49 | 0,43 |
| 3,0 | 1,0 | 0,97 | 0,92 | 0,84 | 0,74 | 0,63 | 0,54 | 0,48 |
| 4,0 | 1,0 | 0,98 | 0,93 | 0,86 | 0,77 | 0,67 | 0,59 | 0,54 |
| 5,0 | 1,0 | 0,98 | 0,94 | 0,88 | 0,80 | 0,71 | 0,64 | 0,60 |
| >6,0 | 1,0 | 0,99 | 0,95 | 0,90 | 0,83 | 0,75 | 0,69 | 0,66 |
| Tỷ số khoảng cách α (là khoảng cách, tâm đến tâm của dầm, cột hoặc xà được chia bởi ít nhất kích thước của khung, dầm hoặc xà được đo theo các góc phái của hướng gió. Đối với khung có cấu trúc tam giác hoặc chữ nhật chéo với gió, tỷ số khoảng cách nên được tính toán từ khoảng cách trung bình giữa các khung trong hướng gió. Hệ số rắn động học được định nghĩa bởi β = ϕa. trong đó: ϕ Tỷ số rắn; a Hằng số; = 1,6 đối với phần tử phẳng; = 1,2 đối với mặt cắt tròn trong khoảng giới hạn và đối với phần tử phẳng; = 0,6 đối với mặt cắt tròn nằm trong phạm vi cực hạn và với phần tử. | ||||||||
8.4.2 Mặt cắt chữ nhật
Hệ số hình dạng đối với phần tử trớn có mặt cắt ngang chữ nhật (b1 ≥ b2, tham khảo Hình 16) có thể lấy bằng:
CS1 = 2KR sinα
|
| khi | b2 ≤ b1 ≤ 2b2 |
| = 1,5KR cosα | khi | b1 > 2b2 |
| KR = 1,0 | khi |
|
|
| khi |
|
| = 0,35 | khi |
|
b1 Cạnh dài hơn của chữ nhật;
b2 Cạnh ngắn hơn của chữ nhật;
r Bán kính góc của mặt cắt;
α Góc giữa cạnh b1 của chữ nhật và dòng trong mặt cắt ngang;
b1, b2 và α cũng được thể hiện trong Hình 16. Đối với mặt cắt ngang hình chữ nhật, tổng hợp lực cản Pd1 được giả định tác động lên một khoảng b1/ 3 từ đầu của mặt phẳng nên được đưa vào tính toán. Xem Hình 16. Hệ số hình dạng và kích thước đặc trưng đối với các phần tử trơn có mặt cắt không đều có thể lấy theo Bảng 7 trong đó kích thước vuông góc với Pd1 và Pd2 cũng được hiểu như cạnh b1 và b2.
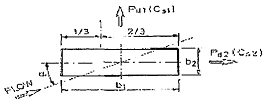
Hình 16 - Lực cản lên mặt cắt tiết diện chữ nhật
8.4.3 Hiệu ứng chiều dài hữu hạn
Hệ số hình dạng C đối với các phần tử riêng lẻ có chiều dài hữu hạn có thể thu được như sau:
|
| (206) |
Trong đó к là hệ số quy đổi như một hàm của tỷ số l/d (có thể lấy từ Bảng 12, trong đó d là kích thước của mặt cắt ngang của 1 phần tử vuông góc với hướng gió và l là chiều dài của phần tử).
Đối với các phần tử tiếp giáp với phần tử khác hoặc một vách nằm cùng một đường với dòng tự do quanh điểm cuối của phần tử bị chặn lại, tỷ số l/d phải được nhân đôi để xác định к. Khi cả hai điểm cuối tiếp giáp, hệ số hình dạng C phải được lấy bằng với phần tử chiều dài vô hạn.
8.4.4 Kết cấu hình cầu và parabol
Đối với kết cấu hình cầu và parabol như chảo ra đa và anten, hệ số hình dạng C có thể được lấy từ Bảng 8.
8.4.5 Sàn đỡ trên mặt phẳng ngang
Đối với các vật thể 3 chiều và các kết cấu tương tự đặt trên một mặt phẳng ngang, hệ số hình dạng có thể lấy từ Bảng 9.
Bảng 7 - Hệ số hình dạng C∞ đối với các mặt cắt ngang không đều
| Dạng | α (độ) | CS1 | CS2 | Dạng | α (độ) | CS1 | CS2 |
|
| 0 | 1,9 | 1,0 |
| 0 | 2,1 | 0 |
| 45 | 1,8 | 0,8 | 45 | 1,9 | 0,6 | ||
| 90 | 2,0 | 1,7 | 90 | 0 | 0,6 | ||
| 135 | -1,8 | -0,1 | 135 | -1,6 | 0,4 | ||
| 180 | -2,0 | 0,1 | 180 | -1,8 | 0 | ||
|
| 0 | 1,8 | 1,8 |
| 0 | 2,1 | 0 |
| 45 | 2,1 | 1,8 | 45 | 2,0 | 0,6 | ||
| 90 | -1,9 | -1,0 | 90 | 0 | 0,9 | ||
| 135 | -2,0 | 0,3 |
|
|
| ||
| 180 | -1,4 | -1,4 |
|
|
| ||
|
| 0 | 1,7 | 0 |
| 0 | 1,6 | 0 |
| 45 | 0,8 | 0,8 | 45 | 1,5 | 1,5 | ||
| 90 | 0 | 1,7 | 90 | 0 | 1,9 | ||
| 135 | -0,8 | 0,8 |
|
|
| ||
| 180 | -1,7 | 0 |
|
|
| ||
|
| 0 | 2,0 | 0 |
| 0 | 1,8 | 0 |
| 45 | 1,2 | 0,9 | 180 | -1,3 | 0 | ||
| 90 | -1,6 | 2,2 |
|
|
| ||
| 135 | -1,1 | -2,4 |
|
|
| ||
| 180 | -1,7 | 0 |
|
|
|
8.4.6 Hệ số ảnh hưởng hình dạng
Hệ số ảnh hưởng hình dạng Ce đối với dầm đơn được cho trong bảng 9.
Bảng 8 - Hệ số hình dạng C đối với những kết cấu có dạng hình cầu
|
| Loại kết cấu | Hệ số hình dạng | |
|
| Bán cầu rỗng, mặt lõm hướng gió | 1,40 | |
|
| Bán cầu rỗng | 0,35 | |
|
| Bán cầu rỗng hoặc đặc, mặt lõm chắn gió | 0,40 | |
|
| Bán cầu đặc và đĩa tròn | 1,20 | |
|
| Bán cầu trên mặt phẳng ngang | 0,50 | |
|
| Hình cầu | Re ≤ 4,2·105 | 0,50 |
| 4,2.105 < Re < 106 | 0,15 | ||
| Re ≥ 106 | 0,20 | ||
| Đối với các vòm cầu rỗng có độ cao f nhỏ hơn bán kính r, có thể nội suy tuyến tính tỷ số f / r giữa những giá trị của một đĩa tròn và một bán cầu | |||
Bảng 9 - Hệ số ảnh hưởng hình dạng Ce cho khung đơn
|
| |||
| Tỷ số rắn ϕ | Hệ số ảnh hưởng hình dạng Ce | ||
| Phần tử có cạnh phẳng | Mặt cắt tròn | ||
| Re < 4,2 x 105 | Re ≥ 4,2 x 105 | ||
| 0,10 | 1,9 | 1,2 | 0,7 |
| 0,20 | 1,8 | 1,2 | 0,8 |
| 0,30 | 1,7 | 1,2 | 0,8 |
| 0,40 | 1,7 | 1,1 | 0,8 |
| 0,50 | 1,6 | 1,1 | 0,8 |
| 0,75 | 1,6 | 1,5 | 1,4 |
| 1,00 | 2,0 | 2,0 | 2,0 |
Tất cả các hệ số hình dạng từ 8.4.1 đến 8.4.5 bao gồm ảnh hưởng của sự hút gió lên mặt khuất gió của phần tử.
Bảng 10 - Hệ số hình dạng C lên mặt phẳng ngang đối với phần thân ba chiều
|
| |||||||||
| Dạng mặt phẳng | l/w | b/d | C cho tỷ số chiều cao/chiều rộng h/b | ||||||
| < 1 | 1 | 2 | 4 | 6 | |||||
|
| ≥4 | ≥4 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | ||
| ≤1/4 | 0,7 | 0,7 | 0,75 | 0,75 | 0,75 | ||||
|
| 3 | 3 | 1,1 | 1,2 | 1,25 | 1,35 | 1,4 | ||
| 1/3 | 0,7 | 0,75 | 0,75 | 0,75 | 0,8 | ||||
|
| 2 | 2 | 1,0 | 1,05 | 1,1 | 1,15 | 1,2 | ||
| 0,5 | 0,75 | 0,75 | 0,8 | 0,85 | 0,9 | ||||
|
| 1.5 | 1,5 | 0,95 | 1,0 | 1,05 | 1,1 | 1,15 | ||
| 2/3 | 0,8 | 0,85 | 0,9 | 0,95 | 1,0 | ||||
| Dạng mặt | l/w | b/d | C cho tỷ số chiều cao/chiều rộng h/b | ||||||
| < 0.5 | 1 | 2 | 4 | 6 | 10 | 20 | |||
|
| 1 | 1 | 0,9 | 0,95 | 1,0 | 1,05 | 1,1 | 1,2 | 1,4 |
| b Kích thước của phần tử vuông góc với gió d Kích thước của phần tử đo theo hướng gió | |||||||||
| Ví dụ A: l = b, w = d. Ví dụ B: w = b, l = d | |||||||||
8.5 Ảnh hướng gió lên sàn sân bay
Áp lực gió lên bề mặt của sàn sân bay có thể được tính toán sử dụng một hệ số áp lực Cp = 2,0 tại cạnh trước của sàn sân bay, giảm tuyến tính tới Cp = 0 tại cạnh sau, lấy theo hướng gió. Áp lực có thể tăng hoặc giảm.
8.6.1 Phân tích gió động
8.6.1.1 Một Phân tích gió động chi tiết xét theo sự thay đổi của lực gió phải được thực hiện với dụng cụ phơi gió và các đối tượng nhạy để thay đổi tải trọng gió. Thông thường, các tháp cao, cần đốt, các giàn như giàn chân căng và giàn neo bằng xích phải được xem xét phân tích
8.6.1.2 Thành phần thay đổi theo thời gian của tải gió có thể gây ra sự cộng hưởng tần số thấp chuyển động dâng, xoay, lắc của các giàn nổi neo bằng xích. Lực gió tần số thấp được tính toán tử một phổ năng lượng gió.
8.6.1.3 Sự thay đổi gió giật của vùng gió có thể được miêu tả là tổng của một thành phần gió dài hàn và một thành phần gió giật. Vận tốc dao động gió giật có thể được miêu tả bằng một phổ gió giật được cho trong mục 5.
8.6.1.4 Sự tương quan (phân phối) theo thời gian của gió giật trên một mặt vuông góc với hướng gió dài hạn có thể được miêu tả bởi một hàm kết hợp sử dụng hệ số giảm ngang, vuông góc với hướng gió dài hạn và một hệ số giảm đứng
8.6.1.5 Lực gió tức thời lên kết cấu chịu tác động gió có thể được tính toán bằng tổng của lực gió tức thời lên mỗi thành phần chịu tác động gió. Áp lực gió tức thời q được tính bằng công thức
|
| (207) |
Trong đó:
u Tốc độ và sự thay đổi hướng gió giật
UT,z Tốc độ gió trung bình
ẋ Vận tốc tức thời của phần tử kết cấu
8.6.1.6 Đối với những tính toán theo miền thời gian, lịch sử thời gian của vận tốc gió theo phổ được cho trong mục 5 có thể được sử dụng kết hợp với các tính toán lực trong 8.6.1.5 để thành lập lịch sử thời gian lực gió.
8.6.1.7 Khi sử dụng một tính toán miền tần số, áp lực gió tức thời có thể tuyến tính hóa:
|
| (208) |
đối với kết cấu có vận tốc ẋ không đáng kể với vận tốc gió. Lực gió dao động là tuyến tính với vận tốc dao động.
8.6.1.8 Trong phân tích miền tần số, nghiệm số có thể lấy được bằng cách nhân mật độ phổ của tải gió động với hàm truyền phản ứng.
8.6.1.9 Trong phân tích miền tần số, một công thức mốt được áp dụng. Phản ứng mốt có thể được kết hợp với phương pháp Căn bậc hai của tổng bình phương (Square-Root-of-Sum-of- Squares - SRSS) nếu các mốt không có sự tương quan. Trong trường hợp các mốt có chu kỳ gần với nhau, phương pháp tổ hợp căn bậc hai được áp dụng.
8.6.1.10 Phương pháp SRSS giả định tất cả giá trị mốt lớn nhất không lệ thuộc vào nhau. Phương pháp CQC giả định tất cả giá trị mốt lớn nhất xảy ra tại cùng một điểm theo thời gian. Giá trị đỉnh của tải trọng được xác định bởi công thức:
|
| (209) |
trong đó: fn là lực mốt tương ứng với mốt n và tổng là toàn bộ mốt. Hệ số chồng mốt ρnm và độ giảm hằng số z.
|
| (210) |
trong đó: r là tỷ số giữa các mốt tần số r = ωn / ωm ≤ 1.
8.6.1.11 Tất cả những ảnh hưởng tương đương như giảm chấn kết cấu, giảm khí động học và giảm thủy động lực phải được xem xét tới trong quá trình phân tích.
8.6.1.12 Đối với thiết kế kết cấu, hiệu ứng tải trọng cực đại do gió tĩnh và động có thể được đánh giá bằng:
| Fe = Fs + gσ(f) | (211) |
Trong đó:
Fs Phản ứng tĩnh do tốc độ gió trung bình thiết kế;
σ(f) Độ lệch Tiêu chuẩn của phản ứng động kết cấu;
g Hệ số đỉnh phản ứng gió.
Dữ liệu thu được từ mô hình tin cậy và đầy đủ được khuyến nghị cho việc xem xét áp lực và kết quả tải trọng lên kết cấu có hình dạng phức tạp.
Việc thử phải được tiến hành với một mô hình có quy mô thể hiện đầy đủ hình dạng kết cấu.
Gió thực phải được mô hình hóa để giải thích sự thay đổi của tốc độ gió trung bình với độ cao trên mặt đất hoặc mặt biển và mức độ nhiễu loạn của gió.
Tải trọng gió lên kết cấu có thể được tính toán sử dụng tính toán động chất lỏng - Computational Fluid Dynamics (CFD), giải quyết phương trình Navier Stokes cho chuyển động không khí, tính toán độ nén và ảnh hưởng nhiễu loạn. Một trong đó phải được biết khi áp dụng CFD để tính toán lực gió lên kết cấu.
- Kết quả có thể phụ thuộc mạnh vào mô hình nhiễu loạn được sử dụng;
- Vận tốc vùng gió đầu vào phải được mô hình hóa bao gồm các ảnh hưởng lớp biên;
- Phần hở ra của kết cấu phải là một phần nhỏ của khu vực chảy ra miền tính toán;
- Độ rõ lưới phải ít nhất bằng 10 ô trên căn bậc hai của thể tích kết cấu và ít nhất 10 ô trên khoảng chia giữa các kết cấu;
- Nghiên cứu hội tụ lưới phải được tiến hành;
- Kết quả phải còn thời hạn với kết quả thử ống gió.
9 Tải trọng do sóng và dòng chảy lên phần tử mảnh
9.1.1 Lực cục bộ lên kết cấu mảnh
Lực thủy động được áp dụng lên kết cấu mảnh chịu tác động của một dòng chất lỏng chung có thể được xác định bằng tổng các lực cục bộ lên từng phần của kết cấu. Véc tơ lực nói chung lên một phần có thể được tách rời thành lực pháp tuyến fN, lực tiếp tuyến fT và lực nâng fL vuông góc với cả fN và fN, xem Hình 17.
9.1.2 Công thức tải trọng Morrison
9.1.2.1 Đối với phần tử kết cấu mảnh có kích thước mặt cắt ngang đủ nhỏ để gra-đi-en của vận tốc và gia tốc phần tử chất lỏng theo hướng vuông góc với phần tử bị bỏ qua, tải trọng sóng có thể được tính toán bằng việc sử dụng công thức Morrision có tổng là một lực quán tính tương ứng với gia tốc và một lực cản tương ứng với bình phương vận tốc.
9.1.2.2 Công thức tải trọng Morrsion được áp dụng khi thỏa mãn điều kiện:
| λ > 5D | (212) |
Trong đó λ là bước sóng và D là đường kính hoặc kích thước mặt cắt của phần tử. Khi chiều dài của phần tử lớn hơn nhiều so với kích thước ngang, tác dụng có thể bỏ qua và tổng lực có thể lấy bằng tổng lực của từng mặt cắt dọc theo chiều dài phần tử.
9.1.2.3 Đối với điều kiện kết hợp sóng và dòng chảy, vận tốc phần tử do sóng và dòng chảy phải được bổ sung đại lượng véc tơ. Nếu có sẵn, việc tính toán toàn bộ vận tốc và gia tốc phần tử dựa trên lý thuyết chính xác sự tương tác sóng/dòng chảy được ưu tiên hơn.
9.1.3 Định nghĩa thành phần lực
Hệ số cản CD là lực cản không thứ nguyên:
|
| (213) |
Trong đó:
fdrag Lực cản cục bộ (N/m);
ρ Mật độ chất lỏng (kg/m3);
D Đường kính (hoặc kích thước đặc trưng) (m);
v Vận tốc (m/s).
Véc tơ vận tốc chất lỏng sẽ có hướng tương ứng với trục của phần tử mảnh (Hình 17). Lực cản fdrag tách thành lực pháp tuyến fN và lực tiếp tuyến fT
Hệ số nước kèm CA là khối lượng nước kèm không thứ nguyên:
|
| (214) |
Trong đó:
ma Khối lượng nước kèm trên đơn vị dài (kg/m);
ρ Diện tích mặt cắt ngang (m2);
Hệ số khối lượng được định nghĩa là:
| CM = 1 + CA | (215) |
Hệ số nâng được định nghĩa là lực nâng không thứ nguyên:
|
| (216) |
Trong đó:
flift Lực nâng cục bộ (N/m)
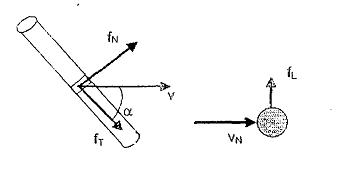
Hình 17 - Định nghĩa lực pháp tuyến, lực tiếp tuyến và lực nâng của phần tử mảnh
9.2.1 Kết cấu cố định chịu tác động sóng và dòng chảy
Lực cục bộ fN lên kết cấu mảnh cố định trong dòng chảy hai chiều vuông góc với trục phần tử được cho bằng:
|
| (217) |
Trong đó:
v Vận tốc phần tử chất lỏng (sóng và/hoặc dòng chảy) )m/s);
![]() Gia tốc phần tử chất lỏng (m/s2);
Gia tốc phần tử chất lỏng (m/s2);
A Diện tích mặt cắt ngang (m2);
D Đường kính hoặc kích thước tiết diện đặc trưng (m);
ρ Mật độ khối lượng của chất lỏng (kg/m3);
CA Hệ số nước kèm (với diện tích mặt cắt ngang như diện tích tham chiếu);
CD Hệ số cản.
9.2.2 Kết cấu di chuyển trong vùng nước tĩnh
Lực cục bộ fN lên kết cấu mảnh di chuyển trong vùng nước tĩnh có được cho như sau:
|
| (218) |
Trong đó:
ṙ Vận tốc của phần tử vuông góc với trục (m/s);
![]() Gia tốc của phần tử vuông góc với trục (m/s2);
Gia tốc của phần tử vuông góc với trục (m/s2);
Cd Hệ số cản thủy động học.
9.2.3 Kết cấu di chuyển trong sóng và dòng chảy
Lực cục bộ fN lên kết cấu mảnh di chuyển trong dòng chảy hai chiều không đều vuông góc với trục phần tử có thể thu được bằng tổng lực phân phối trong 9.2.1 và 9.2.2
|
| (219) |
Công thức này là mô hình miền dòng độc lập (independent flow field model). Trong phân tích phản ứng, để giải r = r(t), lực do nước kèm:
|
| (220) |
Cộng với khối lượng kết cấu nhân gia tốc.
9.2.4 Công thức vận tốc tương đối
Lực cục bộ có thể được viết dưới dạng vận tốc tương đối:
|
| (221) |
hoặc dưới một dạng tương đương khi gia tốc tương đối cũng được kể đến:
|
| (222) |
trong đó:
a = ![]() gia tốc chất lỏng (m/s2);
gia tốc chất lỏng (m/s2);
vr = v - ṙ vận tốc tương quan (m/s);
ar = ![]() gia tốc tương quan (m2/s).
gia tốc tương quan (m2/s).
Khi sử dụng công thức vận tốc tương đối cho lực cản, lực cản thủy động lực bổ sung không nên được tính đến.
9.2.5 Tính áp dụng của công thức vận tốc tương đối
Việc sử dụng công thức vận tốc tương đối cho lực cản là hợp lý nếu r/D >1, trong đó r là biên độ chuyển vị phần tử và D là đường kính phần tử.
Nếu r/D< 1 sự phù hợp phụ thuốc vào giá trị của thông số VR = vTn/D.
20≤vTn/D Vận tốc tương đối đề xuất.
10 ≤ vTn / D < 20 Vận tốc tương đối có thể dẫn đến một đánh giá quá mức cản nếu chuyển vị ít hơn đường kính phần tử.
vTn /D < 10 Được đề xuất để loại bỏ vận tốc kết cấu khi chuyển vị ít hơn một đường kính và sử dụng công thức cản trong 9.2.1.
Đối với mặt phẳng đứng đi qua phần từ trong vùng kết hợp sóng và dòng chảy, vận tốc có thể được tính:
v = vc = pHs/Tz, vận tốc chất điểm xấp xỉ gần mặt sóng (m/s);
vc Vận tốc dòng chảy (m/s);
Tn Chu kỳ dao động kết cấu (s);
Hs Chiều cao sóng đáng kể;
Tz Chu kỳ cắt không.
9.2.6 Lực cản pháp tuyến lên trụ nghiêng
9.2.6.1 Đối với hướng dòng từ 45° đến 90°, nguyên lý dòng vuông góc được giả định. Lực pháp tuyến lên trụ tròn có thể được tính toán sử dụng thành phần pháp tuyến của vận tốc hạt nước.
| vn = vsinα | (223) |
Trong đó α là góc giữa trục của trụ trong và véc tơ vận tốc. Lực cản vuông góc với trụ tròn được cho bởi:
|
| (224) |
9.2.6.2 Về cơ bản CDn phụ thuộc vào số Reynolds và góc tác động. Dòng trước tới hạn và trên tới hạn CDn có thể được lấy độc lập với α. Đối với dòng tới hạn (Hình 21), CDn có thể thay đổi mạnh với hướng dòng.
9.3 Lực tiếp tuyến lên trụ nghiêng
9.3.1 Quy định chung
9.3.1.1 Đối với trụ trơn, lực cản tiếp tuyến chủ yếu do ma sát bề mặt và là nhỏ so với lực cản pháp tuyến. Tuy nhiên đối với các phần tử mảnh dài có vận tốc tiếp tuyến tương đối, lực cản tiếp tuyến là đáng kể.
9.3.1.2 Lực cản tiếp tuyến trên đơn vị dài có thể viết dưới dạng:
|
| (225) |
trong đó: CDt là hệ số cản tiếp tuyến và v là độ lớn của tổng vận tốc. Lực tiếp tuyến cơ bản không tỷ lệ với bình phương của thành phần tiếp tuyến vận tốc vT = vcosα mặc dù được sử dụng trong các mã máy tính. Một vài mã máy tĩnh cũng sử dụng hệ số ma sát bề mặt CDf được định nghĩa bằng công thức:
| CDt = pCDfcos(α) | (226) |
9.3.1.3 Công thức dưới đây CDt có thể được sử dụng phụ thuộc góc giữa véc tơ vận tốc và trục trụ:
| CDt = CDn(m+n.sinα)cosα | (227) |
trong đó CDn là hệ số cản đối với dòng chảy vuông góc. Các giá trị dưới đây cho m và n được dựa trên dữ liệu đã được công bố.
|
| m | n |
| Cáp trần, trụ trơn | 0,02 đến 0,03 | 0,04 đến 0,05 |
| Cáp phẳng | 0,25 đến 0,50 | 0,50 đến 0,25 |
| Dây 6 tao | 0,03 | 0,06 |
9.3.1.4 Đối với các ống đứng có mặt gồ ghề, được khuyến cáo sử dụng m = 0,03 và n = 0,055. Sự thay đổi của CDt với α cho những giá trị của m và n được cho trong 0
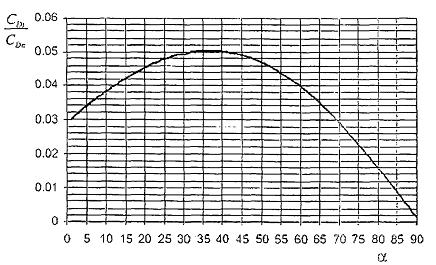
Hình 18 - Sự thay đổi của CDt với góc α
9.4.1 Quy định chung
Lực nâng fL theo hướng vuông góc với hướng dòng chảy chất lỏng, lên kết cấu mảnh có thể do:
- Mặt cắt không đối xứng;
- Ảnh hưởng rẽ nước;
- Ảnh hưởng tường chắn;
- Hiệu ứng xoáy.
9.4.1.1 Mặt cắt bất đối xứng. Lực nâng và lực cản và momen xoắn lên kết cấu mảnh có mặt cắt không đối xứng (tương đương với hướng dòng) có thể dẫn đến biên độ dao động lớn.
9.4.1.2 Ảnh hưởng rẽ nước (wake effects). Dải vận tốc trong vùng rẽ nước của một hoặc vài trụ tròn là không đồng nhất. Vị trí dựa vào lực cản và lực nâng lên trụ tròn trong vùng rẽ nước có thể gây ra dao động do rẽ nước (wake induced oscillations - WIO).
9.4.1.3 Ảnh hưởng tường chắn (wall effects). Dòng chảy không đối xứng lên một trụ tròn gần tường tạo ra một lực nâng khác không. Một khoảng hở hẹp giữa trụ tròn và tường dẫn đến gia tăng vận tốc và giảm áp lực tác động lên tường.
9.4.1.4 Hiệu ứng xoáy. Lực nâng do dao động hiệu ứng xoáy với tần số strouhal. Hướng dẫn hiệu ứng xoáy và xoáy do dao động được cho trong mục 12.
Mô men không nhớt trên đơn vị dài theo trục dọc của một tiết diện không tròn có hai mặt đối xứng là:
|
| (228) |
Trong đó:
v,w Vận tốc hạt chất lỏng theo hướng y và z (m/s);
y,z Vận tốc vuông góc tiết diện theo hướng y và z (m/s);
m66 Mô men quán tính tiết diện (kg x m), xem phụ lục A;
Ω Gia tốc góc của mặt cắt (rad/s2);
![]() Hệ số khối lượng nước kèm theo hướng y và z.
Hệ số khối lượng nước kèm theo hướng y và z.
Việc phân tích phản ứng số hạng mt = -m66Ω cộng với mô men quán tính nhân với gia tốc góc theo phương tay trái của phương trình chuyển động.
9.6 Hệ số thủy động học đối với dòng chảy đều
9.6.1 Thông số điều chỉnh
9.6.1.1 Khi sử dụng công thức tải trọng Morison để tính tải trọng động học lên kết cấu, nên đưa vào tính toán tham số CD và CA như hàm của Re, số Keulegan-Carpenter và độ nhám:
| CD = CD (Re,KC,∆) | (229) |
| CA = CA (Re,KC,∆) | (230) |
Các thông số được định nghĩa như sau:
- Số Reynolds: Re = vD/v;
- Số Keulegan - Carpenter: KC = vmT / D.
- Độ nhám không thứ nguyên ∆ = k / D.
Trong đó:
D Đường kính (m);
T Chu kỳ sóng hoặc chu kỳ dao động (s);
k Chiều cao nhám (m);
v Tổng vận tốc dòng (m/s);
v Độ nhớt động học chất lỏng (m2/s). xem phụ lục C
vm Vận tốc quỹ đạo lớn nhất (m/s)
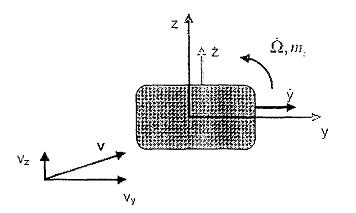
Hình 19 - Mô men xoắn lên tiết diện không tròn
9.6.1.2 Đối với dao động dòng chất lỏng, một hệ số tần số nhớt thường được sử dụng thay thế số Reynolds. Hệ số này được định nghĩa là tỷ số giữa số Reynolds và số Keulegan-Carpenter:
| β=Re/KC=D2/vT=ωD2/(2pv) | (231) |
Trong đó:
D Đường kính (m);
T Chu kỳ sóng hoặc chu kỳ dao động của kết cấu (s);
ω = 2p/T = tần số góc (rad/s);
v Độ nhớt động học chất lỏng (m2/s).
Dữ liệu thí nghiệm đối với CD và CM thu được từ thử ống chữ U thường được cho như hàm của KC và β khi chu kỳ dao động T là không đổi và do đó β là không đổi đối với từng mẫu thử.
9.6.1.3 Đối với trụ tròn, tỷ số của lực cản lớn nhất fD,max và lực quán tính lớn nhất ft,max bằng:
|
| (232) |
Công thức có thể được sử dụng như một chỉ số lực cản hay lực quán tính lớn hơn.
9.6.1.4 Đối với việc kết hợp sóng đều và điều kiện dòng chảy, những thông số chính là số Reynolds dựa trên vận tốc lớn nhất, v = vc + vm, số Keulegan-Carpenter dựa trên vận tốc quỹ đạo vm và tỷ số vận tốc dòng chảy, được định nghĩa như sau:
| αc = vc / (vc + vm) | (233) |
Trong đó vc là vận tốc dòng chảy. Trong một trạng thái biển chung, vận tốc do sóng đáng kể nên được sử dụng thay cho vận tốc quỹ đạo lớn nhất.
9.6.1.5 Đối với dòng chảy có dạng hình sin (điều hòa), số Keulegan-Carpenter có thể được viết như sau:
| KC = 2pƞ0 / D | (234) |
Trong đó ƞ0 là biên độ dao động dòng chảy. Do vậy, số KC là một thước đo khoảng cách đi qua của một hạt chất lỏng trong một nửa chu kỳ tương ứng với đường kính phần tử.
Đối với dòng chất lỏng trong khu vực sóng, ƞ0 trong công thức trên có thể được lấy như biên độ sóng để số KC trở thành:
|
| (235) |
Trong đó H là chiều cao sóng.
9.6.1.6 Đối với kết cấu dao động trong vùng nước tĩnh, ví dụ như phần dưới thấp của ống đứng trong vùng nước sâu, số Keulegan-Carpenter được cho bởi:
|
| (236) |
Trong đó rm là vận tốc lớn nhất của ống đứng, T là chu kỳ dao động và D là đường kính trụ
9.6.2 Hiệu ứng tác động tường chắn
9.6.2.1 Hệ số lực cũng phụ thuộc vào khoảng cách đến một biên cố định được định nghĩa bởi tỷ số khoảng cách giữa trụ và biên cố định (e = H/D), trong đó H là khoảng giữa trụ và biên cố định, xem Hình 23. Hệ số nâng CL đối với dòng quanh một trụ trơn trong vùng cận biên được cho trong Hình 20.
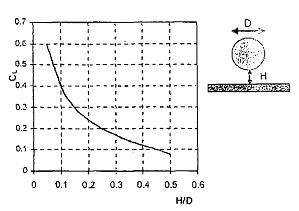
Hình 20 - Hệ số nâng đối với một trụ trơn trong vùng cận biên
9.6.2.2 Một mặt phẳng tự do có thể có ảnh hưởng mạnh lên hệ số nước kèm CA nếu kết cấu gần với mặt phẳng. CA do đó cũng là một hàm của tần số dao động. Thông số tần số không thứ nguyên tương ứng:
| ω(D/g)1/2 | (237) |
trong đó ω là tần số góc của dao động và g là gia tốc trọng trường.
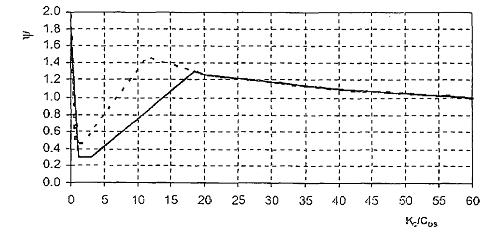
Hình 21 - Hệ số biên độ rẽ nước ѱ như là hàm của số KC đối với trường hợp ống trơn (CDS = 0,65 - nét liền) và ống ráp (CDS =1,05- nét đứng)
9.7 Hệ số cản đối với trụ tròn
9.7.1 Ảnh hưởng của số Reynolds và độ nhám
9.7.1.1 Hệ số cản hai bậc đối với trụ tròn trơn và trụ tròn nhám trong dòng chảy đều là một hàm của số Reynolds được cho trong Hình 22. Hệ số cản giảm nhẹ trong phạm vi số Reynolds nhất định. Đây được gọi là dòng chảy tới hạn và rất rõ ràng đối với trụ tròn trơn.
9.7.1.2 Có 4 chế độ chảy khác nhau: Dòng trước tới hạn, dòng tới hạn, dòng trên tới hạn và dòng chuyển tiếp.
9.7.1.3 Hướng dẫn đối với độ nhám bề mặt được sử dụng cho việc xác định hệ số cản, các giá trị dưới đây có thể được sử dụng.
Bảng 11-Độ nhám bề mặt
| Vật liệu | k (mét) |
| Thép, không có lớp bọc | 5x10-5 |
| Thép, được sơn | 5x10-6 |
| Thép, độ ăn mòn cao | 5x10-3 |
| Bê tông | 5x10-3 |
| Sinh vật biển | 5x10-3đến 5x10-2 |
9.7.1.4 Ảnh hưởng của sự phát triển sinh vật biển và các chi tiết phụ như anode phải được xem xét khi chọn đường kính hiệu dụng và các hệ số cản.
9.7.1.5 Khi số Reynolds (Re > 106) và KC lớn, sự phụ thuộc của hệ số cản lên độ nhám ∆ = k / D có thể lấy bằng:
| CDS(∆)= | 0,65 | ;∆ < 10-4 (trơn) | (238) |
| (29 + 4 · log10 (∆))/20 | ;10-4 < ∆ < 10-2 | ||
| 1,05 | ;∆ > 10-2 (nhám) |
Giá trị trên áp dụng cho cả phân tích sóng đều và không đều.
9.7.1.6 Trong điều kiện chảy sau tới hạn, các hệ số có thể được xem xét độc lập với số Reynolds. Đối với ống đứng hoạt động trong môi trường thiết kế cực hạn, số Reynolds thường trong chảy sau tới hạn.
9.7.1.7 Đối với các tính toán mỏi trong môi trường ít khắc nghiệt, ống đứng có thể thả xuống trong điều kiện chảy tới hạn, tối thiểu đối với những đoạn ống đứng trơn. Tuy nhiên đối với trụ nhám điều kiện cực hạn được chuyển sang số Reynolds thấp hơn để ống đứng vẫn có thể được xem xét trong điều kiện chảy sau tới hạn.
9.7.2 Ảnh hưởng của số Keulegan-Carpenter
9.7.2.1 Sự thay đổi của hệ số cản như một hàm của số Keulegan-Carpenter KC đối với trụ tròn trơn và trụ tròn bị phủ bởi sinh vận biển (nhám) với các số Reynolds sau cực hạn có thể xấp xỉ bằng
| CD = CDS(∆).ѱ(KC) | (239) |
Trong đó hệ số biên độ rẽ nước ѱ(KC) được cho trong Hình 21 và 9.7.2.2. CDS(∆) được cho trong 9.7.1.5. Các áp dụng cho vùng dòng tự do không có sự ảnh hưởng của biên cố định.
9.7.2.2 Đối với số Keulegan-Carpenter thấp (KC < 12) hệ sộ biên độ rẽ nước có thể được lấy bằng (Hình 21)
| ѱ(KC) = | Cp + 0,10(KC - 12) | 2 ≤ KC < 12 | (240) |
| Cp - 1,00 | 0,75 ≤ KC < 2 | ||
| Cp - 1,00 - 2,00(KC - 0,75) | KC ≤ 0,75 |
Trong đó:
Cp = 1,50 - 0,024.(12/CDS - 10)
Với độ nhám trung bình, giá trị tìm được bởi việc nội suy tuyến tính giữa các đường cong trụ trơn và nháp tương ứng với CDS = 0,65 và CDS = 1,05.
9.7.2.3. Hệ số biên độ rẽ nước được định nghĩa ở trên có thể áp dụng cho trụ không tròn với giá trị CDS là hệ số cần ổn định thích hợp cho xi lanh.
9.7.2.4 Hệ số cản đối với dòng chảy tĩnh bằng giá trị tiệm cận với số KC lớn vô cùng. Khi kết hợp song và dòng chảy cùng hướng, độ tăng số KC do dòng chảy phải đưa vào tính toán KC = (vm + vc)T/ D. Trong đó vm là vận tốc sóng lớn nhất và vc là vận tốc dòng chảy. Do đó ảnh hưởng của dòng chảy cùng hướng với chuyển động sóng là để đẩy giá trị CD tới giá trị ổn định CDS.
97.2.5 Khi phân tích động phần ống đứng thấp hơn trong vùng nước sâu với số KC thấp do vận tốc ống đứng thấp, hệ số cản chuyển đổi KC không được vượt quá 0,8 vì lực động học trong vùng nước tĩnh là lực giảm chấn và phải sử dụng một hệ số cản thấp hơn để duy trì.
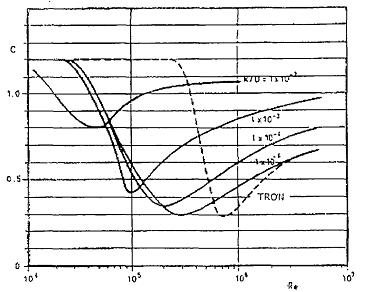
Hình 22 - Hệ số cản của trụ tròn cố định đối với dòng chảy đều có độ nhám thay đổi
9.7.3 Hiệu ứng tác động tường chắn
Để xác định hệ số cản lên trụ tròn gần một biên cố định, hệ số cản được cho trong chất lỏng tự do có thể được nhân lên với một hệ số điều chỉnh lấy được từ Hình 23.
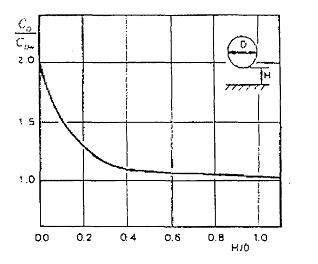
Hình 23 - Tác động của một biên cố định lên hệ số cản của trụ tròn trong dao động dòng sau tới hạn KC > 20, Re=105-2 x 106; CDS là hệ số cản khi H → ∞
9.7.4 Sự phát triển sinh vật biển
Kích thước tiết diện của phần tử kết cấu tăng lên cho độ dày của sinh vật biển. Vì vậy cần đưa vào khi tính các lực lên phần tử mảnh như ống chân đế, ống đứng, ống mềm và conductor. Chiều dày của sinh vật biển phụ thuộc vào vị trí.
Chiều dày sinh vật biển có thể được giả định tăng tuyến tính đưa lên một giá trị tương đương chu kỳ 2 năm sau khi phần tử được lắp đặt ngoài biển.
Đường kính hiệu dụng (hay bề dày tiết diện đối với phần tử không tròn) được cho bởi:
| D = DC + 2t | (241) |
trong đó:
DC Đường kính ngoài trơn;
t Chiều dày của sinh vật biển.
9.7.4.1 Nếu thiếu các thông tin về vị trí xác định, chiều dày sinh vật biển có thể lấy theo:
|
| 56 to 59 ° N | 59 to 72 ° N |
| Độ sâu nước (m) | Chiều dày (mm) | Chiều dày (mm) |
| +2 đến -40 | 100 | 60 |
| Dưới -40 | 50 | 30 |
Khối lượng riêng của sinh vật biển có thể lấy bằng 1325 kg/m3.
9.7.5 Độ khuếch đại cản do VIV
Sự gia tăng hệ số cản do xoáy cắt phải được xem xét tính toán, xem điều 12
9.7.6 Hệ số cản lên tiết diện không tròn
Hệ số cản đối với tiết diện có góc nhọn có thể được đưa vào độc lập với độ nhám. Hệ số cản đối với các tiết diện thay đổi được liệt kê trong Phụ lục B.
9.8 Hệ số quy đổi do chiều dài hữu hạn
Khi ước lượng tổng lực cản lên phần tử mảnh có kích thước mặt cắt đặc trưng d và chiều dài hữu hạn I, tổng tích hợp của lực phân phối lực cắt phải được nhân với một hệ số chuyển đổi theo Bảng 12.
Bảng 12 - Giá trị của hệ số chuyển đổi к lên phần tử mảnh có chiều dài hữu hạn
| A - trụ tròn - dòng trước tới hạn B - trụ tròn - dòng sau tới hạn C - Tấm phẳng song song với dòng | |||||||
| l/d | 2 | 5 | 10 | 20 | 40 | 50 | 100 |
| A | 0,58 | 0,62 | 0,68 | 0,74 | 0,82 | 0,87 | 0,98 |
| B | 0,80 | 0,80 | 0,82 | 0,90 | 0,98 | 0,99 | 1,00 |
| C | 0,62 | 0,66 | 0,69 | 0,81 | 0,87 | 0,90 | 0,95 |
Đối với những phần tử có một mặt tiếp giáp với phần tử khác hoặc một tường nằm trong đường dòng tự do quanh điểm cuối của phần tử bị chặn, tỷ số l/d phải được nhân đôi nhằm xác định к. Khi cả 2 điểm cuối tiếp giáp như đề cập, hệ số cản CD phải được lấy bằng phần tử dài vô hạn.
9.9.1 Ảnh hưởng của số KC và độ nhám
Đối với các trụ nằm trong chất lỏng tự do, xa khỏi mặt phẳng tự do và mặt biển, hệ số khối lượng có thể được áp dụng:
9.9.1.1 Khi KC < 3, CM có thể được giả định độc lập với số KC và bằng giá trị lý thuyết CM = 2 với cả trụ trơn và nhám
9.9.1.2 Khi KC > 3, hệ số khối lượng có thể lấy từ công thức
|
| (242) |
Trong đó CDS được cho theo 9.7.1.5. Sự thay đổi của CM với KC khi trụ trơn (CDS = 0,65) và nhám (CDS = 1,05) được thể hiện trong 0. Đối với độ nhám trung bình, giá trị lấy được từ công thức trên hoặc nội suy tuyến tính giữa các đường cong trụ trơn và nhám
Đường cong trong Hình 24 thu được bởi các dữ liệu thử nghiệm được nêu trong API RP 2A- LRFD
9.9.1.3 Giá trị lý thuyết cho số KC lớn
|
| (243) |
Đối với số KC lớn, lực cản là lực chiếm ưu thế so với lực quán tính
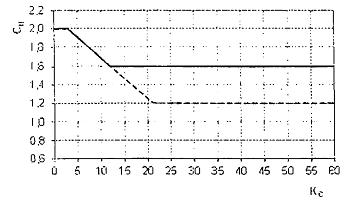
Hình 24 - Hệ số khối lượng như một hàm của KC đối với trụ trơn (nét liền) và trụ nhám (nét đứt)
9.9.1.4 Sự thay đổi của hệ số khối lượng đối với trụ không tròn thu được bằng việc nhân giá trị CM được định nghĩa trong 9.9.1.1 đến 9.9.1.3 với CM0, giá trị lý thuyết của CM với KC triệt tiêu
9.9.2 Hiệu ứng tác động tường chắn
Hệ số khối lượng đối với một trụ tròn gần một biên cố định, được lấy từ Hình 25. Đồ thị áp dụng với chuyển động vuông góc với đường biên cũng như song song với biên. Giá trị phân tích đối với khoảng hở không H/D= 0 là CA = p2/3 -1 = 2,29
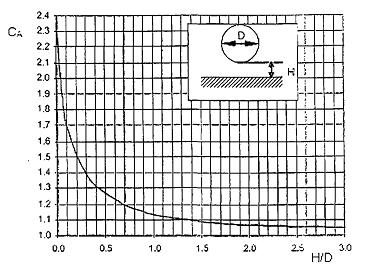
Hình 25 - Giá trị khuyến nghị đối với hệ số nước kèm CA của một trụ tròn trong vùng lân cận của một biên cố định di chuyển vuông góc hoặc song song với biên
9.9.3 Ảnh hưởng của mặt tự do
9.9.3.1 Khối lượng nước kèm của một trụ tròn ngập nước dao động trong vùng lân cận với mặt tự do phụ thuộc lớn vào tần số của dao động ω và khoảng cách tới mặt tự do h (được định nghĩa trong Hình 24). Xem Hình 26.
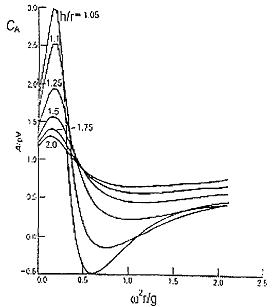
Hình 26 - Hệ số nước kèm đứng đối với trụ tròn tại các khoảng cách khác nhau từ mặt tự do, r là bán kính trụ
9.9.3.2 Hệ Số khối lượng đối với một mặt phẳng xuyên qua trụ đứng được cho bằng
|
| (244) |
trong đó k là số sóng tương ứng với tần số góc của dao động, ω là tương quan lan truyền sóng, R là bán kính trụ và:
|
| (245) |
trong đó J'1 và Y'1 đạo hàm của hàm Bessel bạc nhật. Giới hạn của chu kỳ dài của dao động kR→0 và CM→2.0.
9.9.3.3 Đối với sự đi vào tốc độ cao của một trụ tròn qua một mặt tự do, khối lượng nước kèm có thể lấy như giới hạn tần số cao mA(∞).
Lực va đập sóng được cho bằng:
|
| (246) |
trong đó phần bên tay phải biến mất với vận tốc v không đổi. Biến ma với độ sâu chìm h từ mặt tự do đến tâm của trụ được thể hiện trong Hình 27. Sự xâm nhập nước và va đập (slamming) lên trụ tròn được nêu trong 11.
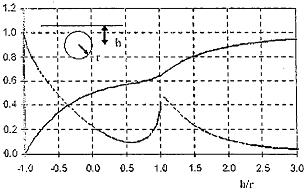
Hình 27 - Giới hạn tần số cao của khối lượng nước kèm và đạo hàm của nó gần với một mặt tự do
Nét liền: ma / ρpr2; nét đứt: (dma / dh) / ρpr
9.10 Hiệu ứng chắn và khuếch đại
9.10.1 Hiệu ứng rẽ nước
9.10.1.1 Lực tác động lên một trụ theo hướng một trụ khác bị ảnh hưởng do một đường rẽ nước tạo ra bởi trụ ngược hướng. Ảnh hưởng chính lên các lực trung bình của trụ cùng hướng là:
- Giảm lực cản trung bình do hiệu ứng chắn;
- Lực nâng khác không do chênh lệch vận tốc trong vùng rẽ nước.
Do đó, lực cản trung bình và hệ số nâng phụ thuộc vào khoảng cách tương ứng giữa các trụ.
9.10.1.2 Vận tốc trong vùng rẽ nước có thể lấy:
| vw(x,y) = v0 - vd(x,y) | (247) |
trong đó v0 biểu thị vận tốc dòng chảy tự do lên ống đứng ngược hướng và vd(x,y) là vận tốc giảm. Đối với một vùng rẽ nước trên tới hạn, công thức sau áp dụng:
Trong đó:
|
| (248) |
Trong đó:
![]()
![]()
k1 và k2 là hằng số thực nghiệm, k1 = 0,25 and k2 =1,0. D là đường kính trụ ngược hướng và CD là hệ số cản của trụ ngược hướng (upstream cylinder). Gốc của hệ tọa độ (x,y) là tâm của trụ ngược hướng, xem Hình 28.
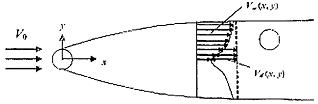
Hình 28 - Hiệu ứng rẽ nước chảy rối theo thời gian trung bình phía sau của một trụ
9.10.2 Hiệu ứng chắn từ nhiều trụ (shielding from multiple cylinders)
9.10.2.1 Đối với một số trụ nằm gần nhau, hiệu ứng nhóm có thể đưa vào tính toán. Nếu không có tài liệu đầy đủ về hiệu ứng nhóm với trường hợp cụ thể, hệ số cản đối với trụ điển hình phải được sử dụng.
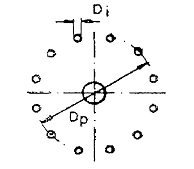
Hình 29 - Các thông số của các dạng trụ điển hình
9.10.2.2 Đối với các kết cầu dầm, dòng chảy có thể bị giảm do sự giao thoa từ kết cấu lên thông lượng của dòng chảy (flow field of the current). Dòng chảy có thể giảm theo:
|
| (249) |
Nhưng không nhỏ hơn 0,7
vc Dòng chảy ổn định được dùng trong tính toán;
vc(∞) Dòng chảy quan trắc;
![]() Hệ số cản của phần tử i;
Hệ số cản của phần tử i;
Di Đường kính của phần tử i;
Dp Bề rộng của kết cấu hoặc nhóm phần tử được xem xét.
9.10.3 Ảnh hưởng của các kết cấu có thể tích lớn
9.10.3.1 Đối với các kết cấu mảnh (như ống đứng) gần với một vật nổi có thể tích lớn, vật nổi cần phải được xác định các ảnh hưởng bức xạ/nhiễu xạ lên động học chất lỏng sóng. Để tính toán ảnh hưởng bức xạ/ nhiễu xạ trong phân tích ULS và FLS, cần tính toán hàm truyền cho vận tốc và gia tốc chất lỏng tại các vị trí được lựa chọn dọc theo kết cấu mảnh, và được áp dụng cho cả hai trường hợp sóng đều và không đều.
9.10.3.2 Đối với ống đứng hoạt động theo động học kết cấu nổi sử dụng công thức tải trọng Morison từ tải trọng thủy động học tác động lên ống đứng phải phù hợp với động học sóng tới. Động học sóng Airy trong vùng dao động nước xuất phát từ sự mở rộng Wheeler có thể được sử dụng hệ số cản được chuyển đổi cho ảnh hưởng KC
9.11 Ống đứng với các phần tử nổi (Risers with bouyancy elements)
9.11.1 Quy định chung
Các hệ số lực thủy động học cho các phần ống đứng nổi phụ thuộc vào:
- Hình học của phần tử nổi;
- Khoảng cách giữa các phần tử;
- Góc nghiêng ống đứng α tương ứng với dòng;
- Thông số dòng (Re, KC).
Khi α nhỏ, dòng tiếp tuyến, hiệu ứng chắn lên các phần có vị trí trong vùng rẽ nước là quan trọng.
9.11.2 Công thức tải trọng Morison đối với phần ống đứng có phần tử nổi
Lực vuông góc và tiếp tuyến lên phần tử ống đứng với các phần tử nổi có thể được viết:
|
| (250) |
|
| (251) |
Trong đó:
![]() Hệ số khối lượng với hướng vuông góc và tiếp tuyến;
Hệ số khối lượng với hướng vuông góc và tiếp tuyến;
![]() Hệ số khối lượng nước kèm với hướng vuông góc và tiếp tuyến (CA = CM -1);
Hệ số khối lượng nước kèm với hướng vuông góc và tiếp tuyến (CA = CM -1);
![]() Hệ số cản với hướng vuông góc và tiếp tuyến;
Hệ số cản với hướng vuông góc và tiếp tuyến;
![]() Các thành phần của gia tốc ống đứng (m/ s2);
Các thành phần của gia tốc ống đứng (m/ s2);
![]() Thành phần của gia tốc hạt sóng (m/s2);
Thành phần của gia tốc hạt sóng (m/s2);
vr Vận tốc tương đối (m/s);
A1 = V/ L, theo diện tích mặt cắt (m2);
D1 = A/L theo đường kính cản (m);
V Thể tích chiếm chỗ của ống đứng và các phần tử nổi của phần ống đứng có chiều dài L (m3);
L Chiều dài của đoạn ống đứng (m);
A Tổng diện tích của diện tích được chiếu với dòng vuông góc (α = 90°) (m2).
9.11.3 Khối lượng nước kèm của phần ống đứng với phần tử nổi
9.11.3.1 Hệ số khối lượng nước kèm ![]() đối với dòng vuông góc qua một phần ống đứng với phần tử nổi có thể ước tính từ hệ số khối lượng nước kèm 2 chiều theo 9.9.
đối với dòng vuông góc qua một phần ống đứng với phần tử nổi có thể ước tính từ hệ số khối lượng nước kèm 2 chiều theo 9.9.
9.11.3.2 Khối lượng nước kèm với từng phần tử nối có thể ước tính bằng:
|
| (252) |
trong đó là Db đường kính ngoài của phần tử nổi và D là đường kính của ống đứng. Hệ số khối lượng nước kèm tiếp tuyến với tổng đoạn ống đứng là:
|
| (253) |
9.11.4 Lực cản lên mặt cắt ống đứng với các phần tử nổi
9.11.4.1 Hệ số cản với dòng vuông góc qua mặt cắt ống đứng với các phần từ nổi có thể ước tính từ hệ số cản hai chiều được hiểu chỉnh từ hiệu ứng chiều dài hữu hạn theo Bảng 11.
9.11.4.2 Hệ số cản tiếp tuyến được xác định bằng
|
| (254) |
Trong đó:
CD1 Hệ số cản của một phần tử nổi đơn với α = 0° và hình dạng, theo diện tích pDb2 / 4;
Db Đường kính của phần tử nổi (m);
N Số phần tử nổi;
I I(KC, N, S / Db) = hệ số tương tác phụ thuộc vào KC, N và khoảng hở phần tử S / Db
Đường cong nét liền S / Db = 2,88
Đường cong nét đứt S / Db = 1,44
Đường cong nét chấm gạch S / Db = 0,87
Hình 31 thể hiện hệ số ảnh hưởng như là hàm của số KC và chiều dài giữa giần từ nổi, từ sổ tay các hệ số thủy động học với ống đứng mềm
Hệ số cản tiếp tuyến với một phần tử đơn là một hàm của chiều dài với tỷ số đường kính được nội suy từ Bảng 13. I là chiều dài của phần tử nổi
Bảng 13 - Hệ số cản tiếp tuyến
| l/Db | 0,5 | 1,0 | 2,0 | 4,0 | 8,0 |
| CD | 1,15 | 0,90 | 0,85 | 0,87 | 0,99 |
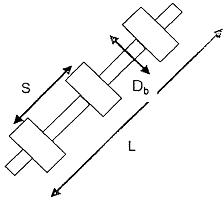
Hình 30 - Kích thước của các phần tử nổi
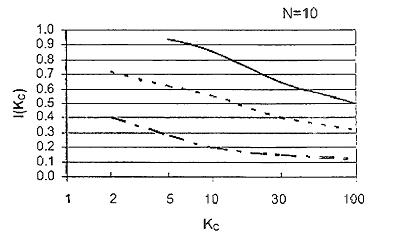
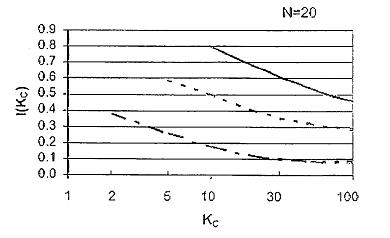
Đường cong nét liền S / Db = 2,88
Đường cong nét đứt S / Db = 1,44
Đường cong nét chấm gạch S / Db = 0,87
Hình 31 - Hệ số tương tác I với số KC khi N = 10, N =20
9.12 Thể tích đối tượng 3D nhỏ
9.12.1 Quy định chung
9.12.1.1 Một loại công thức Morison cũng có thể được áp dụng để ước tính lực cản và lực quán tính lên đối tượng ba chiều chịu sóng và dòng chảy. Các kích thước đặc trưng của đối tượng là nhỏ so với bước sóng được định nghĩa trong 9.1.2
9.12.1.2 Trong công thức tải trọng 9.2.1 đến 9.2.3, diện tích tiết diện A được thay bởi thể tích chiếm chỗ V và kích thước tiết diện (đường kính) D được thay bằng diện tích chiếu S vuông góc với hướng của lực:
|
| (255) |
Hệ số nước kèm cho các đối tượng 3D được cho trong phụ lục A. Hệ số cản được cho trong phụ lục B.
9.12.1.3 Đối với các kết cấu dưới biển đặc trưng được đục lỗ, khối lượng nước kèm có thể phụ thuộc biên độ chuyển động, số KC.
10 Tải trọng phát sinh do sóng và dòng chảy lên các kết cấu lớn
10.1.1 Thuật ngữ kết cấu lớn hữu hạn được dùng cho các kết cấu ngoài khơi với các kích thước D có cùng tỷ lệ độ lớn với bước sóng λ của các con sóng tác động lên kết cấu, luôn là D > λ/6. Tương đương với điều kiện biên được xác định là pD/λ > 0.5.
10.1.2 Một kết cấu lớn có thể được cố định hoặc ở trạng thái nổi. Một số ví dụ về các các kết cấu lớn cố định như các giàn GBS và LNG. Một số ví dụ về các các kết cấu lớn nổi như tàu, kho chứa nổi, giàn chân căng, giàn bán chìm.:
10.1.3 Trong Tiêu chuẩn này tập trung chính vào các tải trọng thủy động và khí động.
10.2 Các chu kỳ dao động riêng
10.2.1 Các chu kỳ dao động riêng Tj, j = 1,2,...6 của một kết cấu ngoài khơi được neo là sấp sỉ bằng:
|
| (256) |
trong đó Mjj, Ajj, Cjj và Kjj là các phần tử đường chéo của các ma trận khối lượng, khối lượng nước kèm, độ cứng thủy tĩnh và neo.
10.2.2 Các chu kỳ dao động riêng có thể phụ thuộc vào việc ghép nối giữa các trạng thái khác nhau và và lượng giảm rung.
10.3 Tải trọng thủy tĩnh và quán tính
Moment quán tính trong Ma trận khối lượng tổng thế được đưa ra bởi:
|
| (257) |
trong đó với x1 = x, x2 = y and x3 = z.
|
| (258) |
Các phần tử đường chéo của ma trận moment quán tính Ijj thường được đưa ra trong phạm vi bán kính của chuyển động quay, r4, r5 và r6,
|
| (259) |
10.4 Tải trung bình và biến đổi chậm
10.4.1 Trong một trạng thái biển ngẫu nhiên đại diện bởi một tổng của N thành phần sóng ωi, i = 1, N lực này dao động ở tần số khác biệt ωi - ωi, và được đưa ra bởi biểu thức
|
| (260) |
trong đó ai, aj là các biên độ sóng đơn và H(2-) là hàm truyền bậc hai (QTF) cho tải tần số khác biệt. Các QTF ở đây được trình bày như một số lượng phức tạp với biên độ |H(2-)| và α(2-). Re biểu thị phần thực.
10.4.2 Lực trôi trung bình
Lực trôi đạt trung bình thu được bằng cách chỉ giữ lại các số hạng chéo (ωi = ωj) trong tổng trên. Lực trôi màu đơn được định nghĩa bởi
|
| (261) |
Các nghĩa lực trôi trung bình hai chiều Fd(ωi,βi,βj) cũng có thể được tính toán từ tiềm năng vận tốc mức đầu tiên.
11 Khoảng tĩnh không và va đập sóng
Các phần của kết cấu gần mặt nước dễ bị lực tác động gây ra bởi sóng va đập.
Va đập sóng có thể tác động lên tổng thể và cục bộ. Tác động của một khối nước lớn từ đỉnh sóng đập sàn là một tác động tải trọng tổng thể trong khi sóng va đập vào một thanh giằng trong vùng dao động sóng là một ảnh hưởng tải cục bộ mà thường không ảnh hưởng đến khả năng làm việc của kết cấu tổng thể.
Va đập là do sự dừng đột ngột của một lượng chất lỏng, sự dừng đó gây ra một lực đáng kể cho hoạt động trên cấu kết.
11.2.1 Định nghĩa
11.2.1.1 Xem xét một kết cấu nổi trong đó khoảng tĩnh không vẫn còn nước, a0, đại diện cho sự chênh lệch về độ cao giữa đáy sàn, hoặc một số phần khác có liên quan của kết cấu, và mực nước trung bình. Khi có sự xuất hiện của sóng và phản ứng của kết cấu gây ra do sóng tương ứng, khoảng tĩnh không tức thời a(x,y,t) tại một vị trí nhất định theo phương ngang (x,y) thay đổi từ giá trị a0.
11.2.1.2 Các khoảng tĩnh không tức thời được định nghĩa bởi:
| a(x,y,t) = a0 + z(x,y,t) - ƞ(x,y,t) | (262) |
trong đó z(x,y,t) là chuyển vị dọc theo phương thẳng đứng của kết cấu tại (x,y) và ƞ(x,y,t) là độ cao bề mặt tức thời ở vị trí nằm ngang.
11.2.1.3 Khoảng tĩnh không âm, a(x,y,t) < 0, có nghĩa là có tác động giữa sóng và cấu kết.
Sau đây là một giải thích vật lý của sự tương tác sóng vỗ sàn, như quan sát đối với một va đập đỉnh sóng trực diện lên kết cấu sàn kiểu hộp đơn giản gắn liền với một giàn cố định kiểu jacket. Nó minh họa cho sự đóng góp chính cho lực tổng thể xác định tác động kết cấu cục bộ và tổng thể và các khoảng thời gian mà lực sóng vỗ sàn lớn nhất và nhỏ nhất.
11.3.1 Lực sóng vỗ sàn ngang
11.3.1.1 Lực sóng vỗ sàn ngang có tham gia của va đập sóng, lực cản và quán tính. Sự tham gia của va đập sóng và lực cản là bậc hai của tốc độ và chi phối bởi các vận tốc hạt sóng cao ở đỉnh. Thành phần quán tính là tỷ lệ thuận với gia tốc hạt chất lỏng. Va đập sóng tham gia trong thời gian ngắn và về 0 ngay sau khi tác động ban đầu.
11.3.1.2 Các hạt chất lỏng bên dưới sàn được gia tốc trong một dòng phun khi các đỉnh sóng chạm sàn. Sự tham gia của lực kéo là tương đối ổn định khí sóng đi qua sàn.
11.3.1.3 Mức độ của thành phần quán tính phụ thuộc vào gia tốc ngang và mức độ thay đổi của diện tích ngập nước theo chiều đứng. Khi gia tốc ngang bằng không tại đỉnh và tăng ở độ cao thấp hơn, sự tham gia của moment quán tính phụ thuộc vào sự ngập của kết cấu.
11.3.1.4 Các lực nước thoát ra âm (0) là do áp suất thấp ở các tường phía trước gây ra bởi vận tốc chất lỏng đi xuống thẳng đứng. Độ lớn của nó phụ thuộc vào vận tốc đỉnh và sự ngập của kết cấu.
11.3.2 Lực sóng vỗ sàn theo phương đứng
11.3.2.1 Lực sóng vỗ sàn theo phương đứng là rất quan trọng cho chi tiệt kết cấu cục bộ vì các lực tác động lên một diện tích nhỏ dẫn đến áp lực nước cục bộ cao. Nó chủ yếu là lực va đập tỷ lệ với chiều dài ngập nước nhân với bình phương vận tốc hạt sóng.
11.3.2.2 Khi sóng chạy dọc theo mặt dưới của sàn, mặt trước sóng gây tải va đập tại mỗi vị trí mới. Độ lớn của tải trọng va đập là lớn nhất ở cạnh dòng chảy và làm giảm vừa phải như sóng chậm đến phía bên kia, gây ra trong một đỉnh lực tổng thể tương đối rộng (0). Các lực tác động tổng thể thẳng đứng đạt cực đại khi đỉnh sóng đi qua mặt trước của sàn, ở khoảng tĩnh không (âm) tối thiểu.
11.3.2.3 Lực quán tính hướng xuống khi sóng đi qua vì gia tốc đứng của chất lỏng tại đỉnh là âm. Trong giai đoạn đầu của chu kỳ sóng, giới hạn quán tính là nhỏ do các diện tích ngập nước nhỏ, và lực quán tính tác động theo hướng ngược lại của lực va đập và lực cản. Khi toàn bộ phần dưới của kết cấu sàn là ngập nước, giới hạn quán tính đạt tối đa do lực khối lượng nước kèm tối đa. Ngay thời điểm này mà đỉnh sóng đã vượt qua tâm của kết cấu và vận tốc thẳng đứng đã được chuyển âm, nghĩa là đi xuống trong cùng một hướng như lực quán tính.
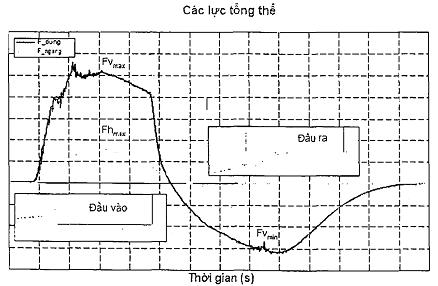
Hình 32 - Tải trọng sóng vỗ sàn thẳng đứng và nằm ngang trên một hộp hình chữ nhật
11.3.2.4 Lực thẳng đứng tại nơi nước thoát ra là phụ thuộc vào chiều dài ngập nước của kết cấu và một mức độ thấp hơn của các điều kiện tác động và sự ngập nước. Va đập sóng không được định nghĩa cho nước thoát ra. Khi dầm lộ ra, các dòng chảy bị xáo trộn, do đó làm giảm chiều dài ngập nước và độ lớn của lực đi xuống xuống theo phương đứng.
11.3.2.5 Khi đánh giá độ cản của kết cấu, điều quan trọng là phải xem xét tính nhất thời của tải sóng vỗ sàn.
11.3.2.6 Cần lưu ý rằng lực áp suất âm trong quá trình thoát nước có nghĩa là áp suất bình thường là thấp hơn so với áp suất không khí, dẫn đến một lực đi xuống.
11.3.3 Phương pháp rút gọn cho lực sóng vỗ sàn ngang
Phương pháp này là một công thức kéo. Quy trình rút gọn dựa trên chiều cao đỉnh nhất định. Các bước để dự đoán lực sóng vỗ sàn và điểm đặt của nó được áp dụng như sau:
11.3.3.1 Đối với một chiều cao đỉnh, tính toán diện tích sàn ngập nước "hình bóng", A, dự theo hướng sóng, θw.
11.3.3.2 A được xác định là khu vực bóng mờ trong Hình 33 nghĩa là khu vực giữa phía dưới sàn giàn giáo và đỉnh của các thiết bị "rắn" trên sàn chính. Các khu vực của chân sàn và giằng sàn phía trên sàn miệng giếng là một phần của diện tích bóng. Diện tích A được tính như sau:
| A = Axcosθw + Aysinθw | (263) |
trong đó θw, Ax và Ay được định nghĩa trong Hình 34.
11.3.3.3 Tính toán vận tốc chất lỏng ngang tối đa do sóng gây ra V ở độ cao đỉnh hoặc phía trên cùng của bóng sàn chính, chọn giá trị nào thấp hơn.
11.3.3.4 Lực ngang của sóng vỗ sàn trên sàn tàu được tính theo công thức sau:
|
| (264) |
trong đó ρ là khối lượng riêng của nước và hệ số lực ngang đối với một sàn (cứng) nhiều thiết bị nặng được đưa ra bởi:
| Ch = | 2,5 cho đầu và hai mạn |
| (265) |
| 1,9 với đường chéo (θw = 45°) |
|
11.3.3.5 Lực Fh nên được áp dụng ở độ cao trên đáy của các sàn miệng giếng, được xác định là 50% của khoảng cách giữa điểm thấp nhất của khu vực bóng và đỉnh sóng hoặc mặt trên của sàn chính cái nào thấp hơn.
11.3.3.6 Phương pháp rút gọn nên được sử dụng cho kết cấu với các bộ phận nhô ra, trong đó nước có thể bị mắc kẹt. Trong trường hợp đó, lực ngang có thể là cao hơn đáng kể, có thể tăng gấp đôi đối với các sóng thẳng hướng và phía bên mạn.
11.3.3.7 Các hệ số lực cũng sẽ lớn hơn cho chiều cao tác động thấp khi có nhiều chướng ngại vật trên mặt dưới sàn, ví dụ một số dầm, đó cách tiếp cận khu vực dự kiến không phản xạ. Trong trường hợp đó, hệ số lực phải lớn hơn, lên đến Ch = 3,5 cho đầu vào sóng.
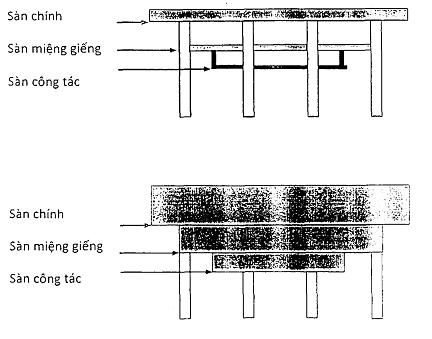
Hình 33 - Định nghĩa diện tích bóng
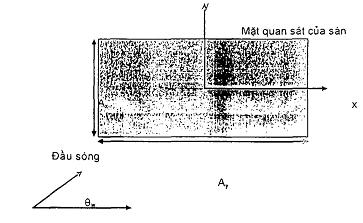
Hình 34 - Quy ước đầu sóng và hướng sóng
11.3.4 Phương pháp động lượng cho lực sóng vỗ sàn theo phương ngang
11.3.4.1 Phương pháp động lượng là một phương pháp mạnh mẽ để dự đoán các lực tác động sóng lên sàn kết cấu. Phương pháp này được giới hạn trong tọa độ hai chiều và một trường sóng đến xáo trộn. Biểu thức cho lực sóng vỗ sàn được đưa ra từ nguyên tắc bảo toàn động lượng chất lỏng.
11.3.4.2 Các lực tác động sóng ngang trên một kết cấu sàn rắn có thể được ước tính giả định rằng các sàn có ảnh hưởng tới một tấm ngắn theo chiều đứng rắn xung quanh ranh giới ngoài của sàn. Khối lượng nước kèm theo tiết diện của một bề mặt tấm thẳng đứng với chiều dài ngập nước theo phương đứng c:
| ma,x = (2/p)ρc2 | (266) |
11.3.4.3 Giả sử rằng giá trị tối đa chiều dài ngập nước theo phương đứng c là nhỏ hơn nhiều so với chiều rộng phương ngang B, vuông góc với hướng truyền sóng, tổng khối lượng nước kèm bên được đưa ra bởi (xem Hình 35):
| Ma,x = (2/p)ρc2B | (267) |
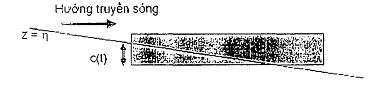
Hình 35 - Định nghĩa chiều dài nhúng nước theo phương đứng
11.3.4.4 Lực ngang trên cơ sở thời gian theo hướng truyền sóng bao gồm cả sự thay đổi đà quán tính và lực kéo được đưa ra bởi:
|
| (268) |
trong đó:
c = c(t) là chiều dài ngập nước theo phương đứng tức thời
u = u(t) là vận tốc hạt ngang tức thời trong sóng xáo trộn
dMa,x / dt = (4/p)ρc(dc / dt)B là tỷ lệ thay đổi của khối lượng nước kèm bên
CD = hệ số cản
11.3.5 Phương pháp rút gọn cho lực tác động sóng theo phương đứng
11.3.5.1 Lực sóng vỗ sàn theo phương đứng tác dụng lên sàn được trang bị nặng hoặc rắn có thể được dự đoán từ vận tốc thẳng đứng trong sóng tại các điểm tiếp xúc đầu tiên và khu vực sàn ngập nước tức thời của các lực tác động thẳng đứng tối đa. Phương pháp này được phát triển đối với một sàn kiểu hộp đơn giản. Đối với các loại cấu hình sàn, chẳng hạn như sàn với các bộ phận nhô ra hoặc nhiều dầm ngang, lực tác động sóng theo phương đứng có thể lớn hơn đáng kể.
11.3.5.2 Đối với một chiều cao đỉnh được xác định từ điều kiện bão cụ thể, xác định pha mà tại đó các phần thấp nhất của sàn va chạm với sóng.
11.3.5.3 Tính toán vận tốc theo phương thẳng đứng (hướng lên), vz, trong sóng tại địa điểm này. Chiều dài sàn ngập nước, L, là khoảng cách ngang từ điểm va chạm đến nơi mà đỉnh sóng là tối đa. Diện tích sàn ngập nước, A, được xác định bởi chiều dài và cấu hình sàn ngập nước, xem Hình 36.
11.3.5.4 Các lực dọc sóng vỗ sàn hướng lên sau đó được tính theo công thức:
|
| (269) |
Trong đó:
Cv = 5 cho đầu sóng vào và cạnh bên
Cv = 10 cho sóng xiên 45°.
11.3.5.5 Lực thẳng đứng hướng lên được phân bố đều trên khu vực sàn ngập nước. Phương pháp rút gọn là hợp lệ cho lực tổng thể. trong khi các lực tác động cục bộ gần như cùng độ lớn xảy ra dọc theo toàn bộ phía dưới sàn.
11.3.5.6 Các lực thẳng đứng hướng xuống cũng cần được xem xét. Độ lớn của lực hướng xuống có thể lớn hơn lực hướng lên nếu phía dưới của sàn là trơn, có thể là trường hợp khi một két đáy lớn hiện diện.
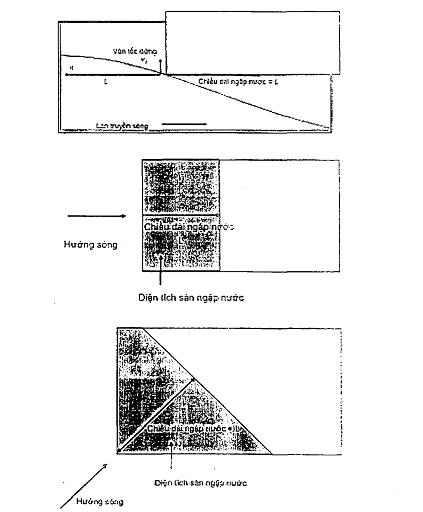
Hình 36 - Định nghĩa về chiều dài ngập nước và vận tốc thẳng đứng trong sóng cho lực tác động theo phương đứng tối đa
11.3.6 Phương pháp động lượng cho lực sóng vỗ sàn thẳng đứng
11.3.6.1 Các lực tác động thẳng đứng trên kết cấu sàn rắn theo phương ngang được đưa ra bởi ảnh hưởng kết hợp của mức độ thay đổi của động lượng và một lực cản. Xấp xỉ một phần ngập nước của kết cấu sàn bởi một tấm phẳng có chiều dài L và chiều rộng B, và giả sử sóng truyền theo một hướng dọc theo chiều dài của tấm, lực tác động theo phương đứng được đưa ra bởi:
|
| (270) |
11.3.6.2 Khối lượng nước kèm ba chiều theo chiều đứng của kết cấu sàn tấm phẳng hình chữ nhật được đưa ra bởi:
|
| (271) |
w = w(t) là vận tốc thẳng đứng ở mặt dưới sàn và L = L(t) là chiều dài ngập nước, số lượng L và dL / dt được xác định từ mức độ tương đối của mức độ ngập nước của mặt dưới sàn phẳng, xảy ra khi sóng tới đi dọc theo sàn từ vị trí tiếp xúc ban đầu của nó.
11.3.6.3 Trong trường hợp trường tự do, nghĩa là cho sàn của một kết cấu jacket, trong đó các sóng đến không bị xáo trộn bởi giàn, số lượng dL / dt có thể xấp xỉ bằng vận tốc pha sóng. wdMa,x / dt thay đổi liên tục đến thời điểm khi chiều dài ngập nước L đạt đến cuối sàn, sau đó dL / dt = 0 và giới hạn từ đó bằng không trong suốt thời gian còn lại mà độ cao sóng cụ thể tiếp xúc với sàn. Giới hạn này cũng được đưa về không khi wz < 0, đó là khi sóng rời sàn. Điều này góp phần vào việc đảo chiều của lực dọc.
11.3.6.4 Giá trị của hệ số cản CD có thể được lấy là 2,0. Giá trị của vận tốc theo phương đứng wz và gia tốc thẳng đứng dwz / dt là tương ứng với vị trí theo phương đứng của sàn. Trong quá trình tác động, chuyển động được tìm thấy tại mỗi thời điểm tại vị trí của tâm hình học của các khu vực ngập nước cần được xem xét.
11.3.6.5 Đối với một hình dạng sàn chung các khu vực ngập nước có thể được xấp xỉ bằng một tấm phẳng với một ranh giới được xác định bởi giao điểm tức thời giữa sàn và sóng tới.
11.3.6.6 Khối lượng nước kèm của tấm có hình tùy ý có thể được xấp xỉ bởi khối lượng nước kèm của một tấm hình elip ở bề mặt tự do. Các trục của elip được tìm thấy bằng cách gán diện tích và tỷ lệ bằng nhau cho hai dạng hình học.
11.3.6.7 Giới hạn tần số cao của khối lượng nước kèm của một tấm hình elip mỏng với trục a/2 và b/2 dao động trong bề mặt tự do được đưa ra bởi một nửa giá trị của nó trong chất lỏng không giới hạn,
|
| (272) |
Trong đó các hệ số CA có thể được tìm thấy bằng cách nội suy ở bảng A-2 trong Phụ lục A
11.3.6.8 Khi sóng chỉ chạm ở sàn, độ chính xác lớn trong cả độ cao sóng và chuyển động hạt chất lỏng cần thiết để dự đoán lực với độ chính xác chấp nhận được. Các lực kết quả cho các tác động nhẹ là dù nhỏ, và các lỗi tuyệt đối trong lực tính toán do đó cũng nhỏ.
11.3.6.3 Phương pháp Kaplan có thể đánh giá thấp tầm quan trọng của lực hướng lên của sóng vỗ sàn vì nhiễu xạ do sàn được bỏ qua và do đó dMa,z/dt được đánh giá thấp.
11.3.7 Phản ứng nhiễu xạ từ kết cấu lớn
11.3.7.1 Một phần mở rộng của phương pháp Kaplan bao gồm các ảnh hưởng nhiễu xạ khối ba chiều lớn bậc 1 và 2, hình học sàn nói chung và hướng sóng đến tùy ý được đề xuất bởi Baarholm (2005).
11.3.7.2 Các ảnh hưởng nhiễu xạ khối lớn có thể là do cột có đường kính lớn hỗ trợ sàn (ví dụ GBS, Semi) hoặc do khác kết cấu lớn trong vùng lân cận của sàn, ví dụ một hàng rào dọc.
11.3.7.3 Khi chuyển động sóng bị ảnh hưởng mạnh mẽ bởi các kết cấu lớn, vận tốc tác động chất lỏng và gia tốc nên được tính bằng cách phân tích nhiễu xạ.
11.3.7.4 Khi một đỉnh sóng chạm sàn, các chuyển động trong sóng dưới sàn được ảnh hưởng mạnh mẽ bởi chính sàn đó. Một dòng phun ảnh hưởng có thể xảy ra, tăng vận tốc hạt chất lỏng ngang với giá trị cao hơn cả vận tốc pha của sóng, vận tốc tăng này cần được tính toán cho đến khi đánh giá tải trên các vật cản nằm trong một khu vực bên dưới sàn tàu. Việc mở rộng theo chiều dọc của trường vận tốc nhiễu loạn là phụ thuộc vào độ trơn của kết cấu, ví dụ bể đáy hoặc dầm, và ngâm của kết cấu.
11.4 Tải tác động do sóng lên kết cấu mảnh
11.4.1 Phương pháp rút gọn
11.4.1.1 Đối với một phần tử kết cấu hình trụ lực va đập lên mỗi đơn vị chiều dài có thể được tính như sau:
|
| (273) |
Trong đó Fs là lực va đập trên đơn vị chiều dài theo hướng của vận tốc, ρ là khối lượng riêng của chất lỏng, Cs là hệ số va đập, D là đường kính phần tử thanh, v là vận tốc tương đối giữa nước và phần tử thanh vuông góc với bề mặt phần tử thanh.
11.4.1.2 Đối với một trụ tròn nhẵn những hệ số va đập có thể được lấy là Cs = 5,15.
11.4.1.3 Nếu các ảnh hưởng động rất quan trọng cả đầu vào nước và các pha đầu ra nên được mô hình hóa.
11.4.2 Va đập sóng trên kết cấu mảnh theo phương ngang
11.4.2.1 Một phương pháp để dự đoán thời gian lịch sử lực va đập sóng ngang lên kết cấu mảnh được đưa ra bởi Kaplan. Giả sử sóng truyền thông thường đối với hình trụ theo phương ngang, lực dọc trên một đơn vị chiều dài của trục có thể được thể hiện bằng cách:
|
| (274) |
Trong đó:
ρgA1 là lực nổi
![]() đại diện cho ảnh hưởng của gradient áp lực không gian trong sóng
đại diện cho ảnh hưởng của gradient áp lực không gian trong sóng
ma,3 là khối lượng nước kèm theo phương đứng đó là một hàm của mức độ ngập nước (như là A1)
d(z/r) là khác nhau chiều dài mặt cắt ngang tham khảo để đánh giá lực cản (với một giá trị tối đa bằng với đường kính hình trụ). Xem Hình 37.
![]() là một hệ số cản cho dòng chảy thẳng đứng, là hàm của mức độ ngập nước, nhưng có thể được thực hiện để có một giá trị không đổi 1,0
là một hệ số cản cho dòng chảy thẳng đứng, là hàm của mức độ ngập nước, nhưng có thể được thực hiện để có một giá trị không đổi 1,0
11.4.2.2 Các điều khoản liên quan đến m3 được tìm thấy từ tỷ lệ thời gian sự thay đổi của lực chất lỏng dọc; và số hạng cuối cùng trong công thức đại diện cho một lực cản. Các số hạng quán tính tỷ lệ với ƞ2 là chỉ để ước lượng khi ƞ > 0, tương ứng với tình trạng tăng độ ngập, khi ƞ < 0 giá trị này được đặt là không.
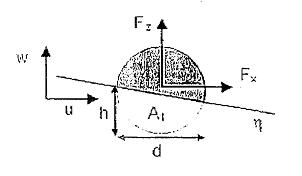
Hình 37 - Va đập sóng lên hình trụ theo phương ngang
11.4.2.3 Một biểu thức tương tự có sẵn cho các lực tác động ngang lên mỗi đơn vị chiều dài:
|
| (275) |
Trong đó:
ma,1 là khối lượng nước kèm theo phương ngang (ma,1=ρpR2)
u là vận tốc hạt chất lỏng ngang
h(z/r) là chiều dài chiếu thẳng đứng thay đổi theo độ ngập nước và có một giá trị tối đa bằng với đường kính hình trụ
![]() là hệ số cản sườn, mà tính chất vật lý khác nhau phù hợp với mức độ ngập nước, nhưng có thể được xem như là các giá trị không đổi 1,0.
là hệ số cản sườn, mà tính chất vật lý khác nhau phù hợp với mức độ ngập nước, nhưng có thể được xem như là các giá trị không đổi 1,0.
Đối với một trụ tròn, tốc độ thay đổi của khối lượng nước kèm ngang được đưa ra bởi ![]()
11.4.3 Va đập sóng lên kết cấu mảnh theo phương dọc
11.4.3.1 Lực va đập vào một hình trụ thẳng đứng có thể dự đoán theo một cách được gọi là strip-wise bằng cách tổng hợp các lực tác động lên mỗi dải của hình trụ như nó thâm nhập vào bề mặt sóng.
11.4.3.2 Lực Fx ở độ cao z khi sóng đánh hình trụ tỷ lệ với động lượng khối lượng nước kèm:
|
| (276) |
A2D là giới hạn tần số cao trong đó của khối lượng nước kèm đối với một phần hình trụ 2D như một chức năng của sự ngập nước s = s(t) so với bề mặt sóng và u là vận tốc ngang tương đối giữa bề mặt sóng và hình trụ. u được giả định không đổi trong quá trình tác động.
11.4.3.3 Giá trị thực nghiệm cho tốc độ thay đổi của khối lượng nước kèm của một hình trụ tròn đối với khoảng cách s là xác định được và đã được đại diện bởi một công thức phân tích bởi Campbell và Weynberg. Hệ số va đập hay hệ số tác động được định nghĩa bởi:
|
| (277) |
trong đó là D đường kính hình trụ. Một sự phù hợp phân tích cho các thí nghiệm đưa ra:
|
| (278) |
11.4.3.4 Tại thời điểm bắt đầu tác động Cs(s) = 5,15. Các mô hình trên là một xấp xỉ đáng tin cậy khi sóng tác động vào là dốc. Công thức trên chỉ được áp dụng trong quá trình xâm nhập của các bề mặt sóng, nghĩa là cho 0 < s < D. Khi hình trụ là hoàn toàn ngập nước, CS(D) = 0,8
11.4.3.5 Các công thức trên cho các lực tác động phân bố dọc theo các hình trụ. Khi phần hình trụ là hoàn toàn ngập nước, mô hình tải phù hợp là phương trình Morison thông thường với khối lượng và lực cản sử dụng khối lượng và hệ số cản không đổi.
11.5 Tải trọng tác động đo sóng lên các tấm
11.5.1 Tải va đập sóng trên một thân cứng
11.5.1.1 Các thông số đặc trưng va đập vào một thân cứng với một góc deadrise nhỏ là vị trí và giá trị của áp lực tối đa, khoảng thời gian và phạm vi không gian của áp lực va đập cao. 0 cung cấp một cái nhìn sơ đồ nhập cảnh nước của một thân hai chiều lên một bề mặt tự do bình tĩnh. Các bề mặt tự do bị biến dạng dẫn đến phun và sự hình thành của một dòng phun.
11.5.1.2 Các góc deadrise cục bộ là một tham số quan trọng, nhưng ảnh hưởng cong cục bộ và lịch sử thời gian của góc deadrise và độ cong vật chất. Ba chiều các ảnh hưởng sẽ có xu hướng giảm áp lực va đập. Cách đỡ các ảnh hưởng có thể làm giảm đáng kể áp lực cao điểm khi góc giữa thân tác động vào và bề mặt tự do thấp hơn 2-3°.
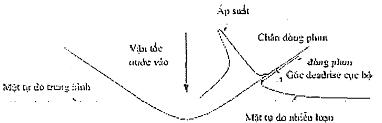
Hình 38 - Sơ đồ hiển thị đầu vào nước của một thân lên một bề mặt tự do tĩnh
11.5.1.3 Hình 39 trình bày định nghĩa của các thông số đặc trưng áp lực va đập vào một thân hình nêm cứng trong quá trình nước tác động vào. Các thân đi vào bề mặt tự do không bị xáo trộn với một vận tốc không đổi V hướng xuống. Các bề mặt tự do trung bình nằm tại z = 0 và chân dòng phun là (ymax, zmax).
β góc deadrise
CPmax hệ số áp lực ở áp suất tối đa
zmax z -phối hợp của áp lực tối đa
∆SS Phạm vi không gian của áp lực va đập quá 50% áp lực tối đa
F3 Lực thủy động lực dọc trên thân
t Thời gian
11.5.1.4 Chiều dài ngập nước của một nêm đối xứng (từ đỉnh đến chân dòng phun) có thể được ước tính bằng công thức
|
| (279) |
Trong đó góc deadrise thấp được đưa ra: β < 15 - 20°
11.5.1.5 Trình bày các giá trị cho tham số đặc trưng của áp lực va đập, bao gồm tổng lực thủy động lực dọc, z -phối hợp của các áp lực tối đa và phạm vi không gian của áp lực va đập vượt quá 50% của áp lực tối đa. Khi góc deadrise β là dưới đây về 20°, phân bố áp suất có một cao điểm rõ rệt gần chân dòng phun.
11.5.1.6 Các thí nghiệm có thể cần thiết để cung cấp cho ước lượng chính xác tải trọng tác động.
11.5.2 Lực va đập không gian trung bình
11.5.2.1 Áp lực cao nhất trong khoảng thời gian nước vào của một cái nêm với một góc deadrise nhỏ thường là không có liên quan về thép kết cấu. Như mô tả trong 11.5.1 đỉnh cao áp được bản địa hóa trong thời gian và không gian.
Bảng 14 - Tính các thông số với một góc deadrise nhỏ thường là không có liên quan về thép kết cấu
| β | CPmax | zmax / Vt | ∆SS / c | F3 / ρV3t |
| 4° | 503,030 | 0,5695 | 0,0150 | 1503,638 |
| 7,5° | 140,587 | 0,5623 | 0,0513 | 399,816 |
| 10° | 77,847 | 0,5556 | 0,0909 | 213,980 |
| 15° | 33,271 | 0,5361 | 0,2136 | 85,522 |
| 20° | 17,774 | 0,5087 | 0,4418 | 42,485 |
| 25° | 10,691 | 0,4709 |
| 23,657 |
| 30° | 6,927 | 0,4243 |
| 14,139 |
| 40° | 3,266 | 0,2866 |
| 5,477 |
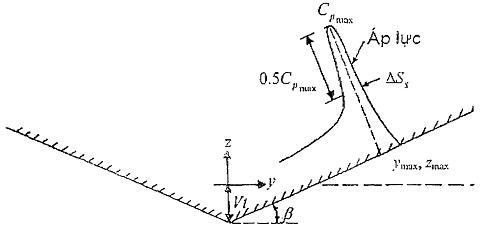
Hình 39 - Định nghĩa góc deadrise nhỏ
11.5.2.2 Áp lực va đập trung bình trên một diện tích rộng lớn hơn (ví dụ: một số lĩnh vực tấm của một con tàu) có thể được tính từ:
|
| (280) |
Trong đó:
ps áp lực va đập trung bình không gian;
ρ khối lượng riêng của chất lỏng;
CPa hệ số áp lực va đập trung bình không gian;
v vận tốc bình thường tương đối giữa nước và bề mặt.
11.5.2.3 Các hệ số áp lực va đập trung bình không gian phải được xác định bằng phương pháp lý thuyết và/hoặc thử được công nhận.
11.5.2.4 Đối với một trụ tròn mịn hệ số áp lực va đập không nhỏ hơn CPa = 5,15. Đối với va đập sóng lên đáy phẳng có tính đến đệm và các phản ứng ba chiều, hệ số áp lực va đập không nhỏ hơn CPa = 2p. Điều này áp dụng cho góc deadrise β < 4°.
11.5.2.5 Đối với một thân hình nêm với góc deadrise β > 15°, tính đến phản ứng ba chiều, hệ số áp lực va đập không nhỏ hơn:
|
| (281) |
trong đó β là góc nêm tại nơi giao nhau giữa thân và mặt nước. Công thức thực nghiệm này là dựa trên một đường cong phù hợp của áp lực đỉnh trong Hình 40.
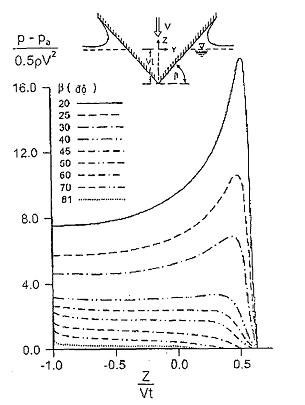
Hình 40 - Dự đoán phân bố áp suất (p) trong quá trình xâm nhập nước của một nêm cứng với vận tốc vít dọc V. Pa = áp suất khí quyển, β = góc deadrise
11.5.2.6 Đối với một thân có hình nêm với 0 < β < 15°, có tính đến các phản ứng đệm và ba chiều, một nội suy tuyến tính giữa các kết quả cho đáy phẳng (CPa = 2p với β = 0°) và β = 15° có thể được áp dụng, xem Hình 41.
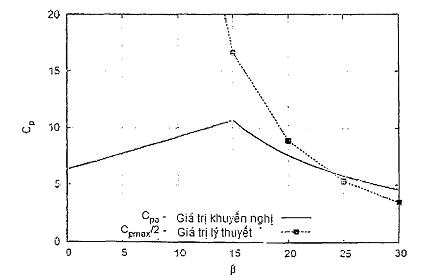
Hình 41 - Áp lực va đập trung bình không gian hệ số CPa so với CPmax / 2 đối với một thân hình nêm như một chức năng của góc deadrise cục bộ β
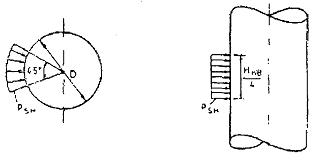
Hình 42 - Diện tích được xem xét trong việc đánh giá tải trọng do áp lực sốc lên các hình trụ tròn
11.6.1 Áp lực sốc
11.6.1.1 Áp lực sốc do sóng vỡ trên bề mặt thẳng đứng phải được xem xét. Các quy trình được mô tả trong 11.4.3 có thể được sử dụng để tính toán áp lực sốc. Các hệ số Cs phụ thuộc vào cấu hình của khu vực tiếp xúc với áp lực sốc.
11.6.1.2 Đối với sóng không bị xáo trộn vận tốc tác động (u) cần được thực hiện ở mức 1.2 lần vận tốc pha của sóng vỡ cao nhất có thể xảy ra nhất trong n năm. Lớn nhất có thể xảy ra nhất bẻ chiều cao sóng có thể được thực hiện như là 1,4 lần so với khả năng cao nhất lớn nhất chiều đáng kể cao sóng trong n năm. Đối tác động trong vùng lân cận của một kết cấu lớn, vận tốc tác động bị ảnh hưởng bởi các phản ứng nhiễu xạ.
11.6.1.3 Đối với một tròn hình trụ thẳng đứng, diện tích tiếp xúc với áp lực sốc có thể được thực hiện như là một tiết diện nghiêng 45° với một chiều cao 0,25 Hb, trong đó Hb là chiều cao sóng vỡ lớn nhất có tần suất xảy ra lớn nhất trong n năm. Vùng từ mực nước tĩnh lên đỉnh của đỉnh sóng nên được tính toán cho ảnh hưởng các áp lực sốc.
11.6.1.4 Đối với một sóng chìm vỡ ngay trước mặt của hình trụ thẳng đứng đường kính D, thời gian T của lực tác động vào các hình trụ có thể được tính như sau:
|
| (282) |
trong đó là c vận tốc pha của sóng.
11.7 Tổn thương mỏi do tác động sóng
11.7.1 Quy định chung
Các tổn thương mỏi do sóng va đập có thể được xác định theo các quy trình sau đây:
a) Xác định chiều cao sóng tối thiểu Hmin mà có thể gây ra sập
b) Chia phân bố chu kỳ dài của các chiều cao sóng, vượt, Hmin, theo một số lượng dải hợp lý
c) Đối với mỗi dải ứng suất được tính như sau:
|
| (283) |
trong đó:
σslam Ứng suất trong các phần tử chịu tải va đập
σb Ứng suất do lực nổi ròng trên phần tử
σw Ứng suất do các lực sóng dọc trên các phần tử
A Hệ số kể đến khuếch đại động.
d) Đóng góp cho mỏi từ mỗi khối sóng được đưa ra như:
|
| (284) |
Trong đó:
nj số sóng trong khối j
Nj số tới hạn của chu kỳ ứng suất (từ đường cong S-N có liên quan) liên quan tới ∆σj
ni số lượng các ứng suất vượt quá phạm vi ứng suất giới hạn liên quan với mức độ cắt của đường cong S-N
R hệ số giảm trên số lượng các con sóng.
k độ dốc của đường cong S-N (ở thang tỷ lệ log-log)
Phương pháp của Ridley có thể được sử dụng để ước tính tổn thương mỏi các kết cấu mảnh nghiêng trong vùng dao động sóng.
12 Dao động gây ra bởi dòng xoáy cảm ứng
12.1 Khái niệm và định nghĩa cơ bản
12.1.1 Khái niệm chung
Gió, dòng chảy hoặc dòng chất lỏng qua một thành phần cấu trúc có thể gây ra mô hình dòng chảy không ổn định do dòng xoáy cảm ứng. Điều này có thể dẫn đến dao động của các phần tử thanh mảnh bình thường quanh trục dọc của chúng. Dao động do dòng xoáy gây ra như vậy (VIO) phải được kiểm tra, phân tích.
Các thông số chủ yếu chi phối dao động do xoáy gây ra là:
a) Tỷ lệ hình học (L / D)
b) Tỷ lệ khối lượng (m* = m / (1/4pρD2)
c) Tỷ lệ tắt dần (z)
d) Số Reynolds (Re = uD/v)
e) Tốc độ giảm (VR = u / fnD)
f) Đặc tính dòng chảy (thông số dòng chảy, dòng chảy ổn định/ dao động, cường độ bất ổn (σu / u ) vv).
Trong đó:
L Chiều dài phần tử (m)
D đường kính phần tử (m)
m Khối lượng trên đơn vị dài (kg/m)
z tỷ lệ giữa sức cản và sức cản Tiêu chuẩn
ρ mật độ chất lỏng (kg/m3)
v độ nhớt động chất lỏng (m2/s)
u (trung bình) dòng chảy vận tốc (m/s)
fn Tần số dao động riêng của các phần tử (Hz)
σu độ lệch chuẩn của vận tốc dòng chảy (m/s)
12.1.2 Số Reynolds
Với các phần tử tĩnh mịn được làm tròn thủy động lực hiện tượng dòng xoáy cảm ứng phụ thuộc rất nhiều vào số Reynolds cho dòng chảy, như được đưa ra dưới đây.
| 102 < Re < 0,6·106 | Định kỳ |
| 0,6·106 < Re < 3·106 | Ngẫu nhiên rải tần số rộng |
| 3·106 < Re < 6·106 | Ngẫu nhiên rải tần số hẹp |
| Re > 6·106 | Tựa như định kỳ |
Đối với phần tử thô và các phần tử dao động trơn tru, xoáy cảm ứng dòng xoáy cảm ứng được xem xét định kỳ cẩn thận trong toàn bộ phạm vi số Reynolds.
12.1.3 Tần số xoáy
Các tần số xoáy trong dòng chảy ổn định hoặc dòng chảy với số KC lớn hơn 40 có thể được tính như sau:
|
| (285) |
Trong đó:
fs tần số dòng xoáy cảm ứng (Hz)
St số Strouhal
u vận tốc chất lỏng bình thường so với trục phần tử thanh (m/s)
D đường kính phần tử (m)
12.1.3.1 Dòng xoáy cảm ứng có liên quan đến các hệ số cản của các phần tử được xem xét. Hệ số cản lớn thường đi cùng dòng xoáy cảm ứng xoáy cảm ứng mạnh hoặc ngược lại.
12.1.3.2 Đối với một hình trụ trơn đứng yên, số Strouhal (St) là một hàm của số Reynolds (Re). Mối quan hệ giữa St và Re đối với một trụ tròn được cho trong Hình
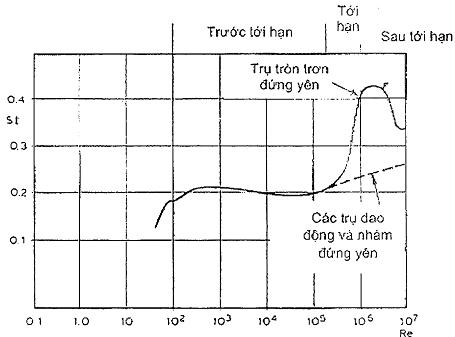
Hình 43 - Số strouhal (St) đối với một hình trụ tròn như một hàm của số Reynolds (Re)
12.1.3.3 Trụ có bề mặt nhám hoặc hình trụ rung (cả mặt trơn và ráp) có số Strouhal tương đối không nhạy cảm với số Reynolds.
12.1.3.4 Đối với mặt cắt ngang với các góc sắc nét, dòng xoáy cảm ứng cũng được xác định cho tất cả các vận tốc, đưa ra số strouhal độc lập với số Reynolds.
12.1.4 Lock-in
12.1.4.1 Tại các vận tốc dòng chảy Tiêu chuẩn đã biết, tần số dòng xoáy cảm ứng có thể trùng với tần số dao động riêng của chuyển động của các phần tử, dẫn đến rung động cộng hưởng.
12.1.4.2 Khi vận tốc dòng chảy được tăng hoặc giảm để các tần số dòng xoáy cảm ứng fs tiếp cận tần số dao động riêng fn, dòng xoáy cảm ứng khóa tần số tần số dao động riêng của kết cấu và những rung động kết quả xảy ra tại hoặc gần với Tần số dao động riêng. Cần lưu ý rằng tần số riêng trong quá trình lock-in có thể khác với tần số riêng trong nước tĩnh. Điều này là do sự thay đổi của khối lượng nước kèm với vận tốc dòng chảy.
12.1.4.3 Trong khu vực lock-in, các xoáy tần số đổ được quyết định bởi tần số riêng của phần tử, trong khi với vận tốc thấp hơn và cao hơn tần số dòng xoáy cảm ứng tuân theo mối quan hệ strouhal.
12.1.4.4 Lock-in cho tần số riêng có thể xảy ra cả song song với dòng chảy (in-line) và ngang với dòng chảy (dòng chảy chéo).
12.1.4.5 Đối với hình trụ mềm đáp ứng ở nhiều dạng, Sự đáp ứng được ở dải rộng điển hình và lock-in được bác là không xảy ra.
12.1.5 chuyển động ngang dòng và trong dòng
Xoáy gây ra rung có thể được chia thành:
- Dao động dòng ngang (CF) với biên độ dao động trong khoảng 1 đường kính
- Dao động trong dòng (IL) với biên độ theo thứ tự từ 10-15% đường kính
- CF gây ra rung động IL với biên độ 30-50% của biên độ CF.
- Chuyển động IL sẽ xảy ra ở vận tốc giảm thấp nhất, và sẽ là phản ứng đầu tiên xảy ra. Khi vận tốc đủ lớn cho phản ứng CF (và CF gây ra phản ứng IL) xảy ra, chuyển động IL là bình thường không còn quan tâm từ khi biên độ phản ứng là nhỏ hơn.
12.1.6 Vận tốc giảm
Để xác định vận tốc dao động trong đó dòng xoáy cảm ứng sẽ cộng hưởng với tần số riêng của phần tử, một tham số VR, được gọi là vận tốc giảm, được sử dụng. VR được định nghĩa là:
|
| (286) |
trong đó:
u = u(x) dòng chảy vận tốc tức thời bình thường với trục phần tử (m/s)
fi các tần số dao động riêng thứ i của các phần tử thanh (Hz)
D = D(x) đường kính phần tử thanh (m)
x khoảng cách dọc theo trục phần tử
12.1.7 Tỷ lệ khối lượng
Tỷ lệ khối lượng là thước đo tầm quan trọng tương đối của sự nổi và các phản ứng khối lượng trên mô hình, và được định nghĩa là:
|
| (287) |
Điển hình, những rung động xảy ra trên phạm vi vận tốc giảm 3 < VR <16 để có tỷ lệ khối lượng thấp (ví dụ các ống đứng, đường ống), trong khi đối với tỷ lệ khối lượng cao rung động xảy ra trong khoảng từ 4 < VR < 8 (gió tiếp xúc kết cấu).
12.1.8 Tham số ổn định
Một thông số làm chủ các chuyển động là tham số ổn định, Ks. Nó cũng được gọi là số Scrouton.
Tham số này là tỷ lệ thuận với sức cản và tỷ lệ nghịch với lực do dòng xoáy cảm ứng. Do đó tham số là lớn khi sức cản là lớn hay nếu các khu vực lock-in trên các phần tử là nhỏ so với chiều dài của ống.
Đối với đường kính phần tử đồng nhất và điều kiện dòng chảy đồng đều trên chiều dài phần tử tham số ổn định được định nghĩa là:
|
| (288) |
Trong đó:
ρ khối lượng riêng xung quanh trung bình (không khí/khí hoặc chất lỏng) (kg/m3)
D đường kính phần tử (m)
me khối lượng trên một đơn vị chiều dài của các phần tử (kg/m)
δ sức cản logarit (= 2pz)
z tỷ lệ giữa sức cản và sức cản Tiêu chuẩn
δ δs + δother + δn
δs sức cản kết cấu
δother sức cản đất hoặc sức cản khác
δh sức cản thủy động lực
12.1.9 Sức cản kết cấu
sức cản kết cấu là do các lực ma sát của vật liệu phần tử và phụ thuộc vào mức độ căng và độ lệch liên quan. Đối với phần tử thép tiếp xúc gió, tỷ lệ sức cản cấu trúc (δs/2p) được lấy là 0,0015, nếu không có các thông tin khác có sẵn. Đối với phần tử mảnh trong nước, tỷ lệ sức cản kết cấu bị lệch vừa phải được lấy điển hình từ 0,005 cho ống thép nguyên chất đến 0,03-0,04 cho ống mềm.
12.1.10 Sức cản thủy động lực
12.1.10.1 Lượng giảm lo-ga-rit tổng quát cho các sức cản thủy động lực học có thể được tính như sau:
|
| (289) |
Mi là khối lượng tổng quát cho chế độ i:
|
| (290) |
Trong đó:
m = m(x), khối lượng trên đơn vị dài bao gồm cả lượng khối kết cấu, khối lượng nước kèm, và lượng thể tích của bất kỳ chất lỏng chứa trong các phần tử (kg/m)
L chiều dài của phần tử (m)
y(x) hình chế độ bình thường
12.1.10.2 Hệ số cản CD là một hàm của x. Các giới hạn không thể thiếu (l1, l1, + ∆ và d) được định nghĩa trong Hình 44.
![]() là tổng quát sụt logarit của sức cản thủy động lực bên ngoài khu vực lock-in cho rung động dòng chảy chéo. Sự đóng góp để sức cản thủy động lực học trong khu vực lock-in được thiết lập để không nằm trong tính toán của KS.
là tổng quát sụt logarit của sức cản thủy động lực bên ngoài khu vực lock-in cho rung động dòng chảy chéo. Sự đóng góp để sức cản thủy động lực học trong khu vực lock-in được thiết lập để không nằm trong tính toán của KS.
Đối với dòng chảy xoáy gây ra rung động chéo δh = ![]() , và trong dòng xoáy gây ra rung động sự đóng góp là kép, tức là
, và trong dòng xoáy gây ra rung động sự đóng góp là kép, tức là
![]() .
.
12.1.11 Khối lượng phản ứng
khối lượng phản ứng trên một đơn vị chiều dài của các phần tử được tính bằng:
|
| (291) |
Các khối lượng nước kèm vào vào biểu thức m có thể được xác định từ các biểu thức trong 9. Các khối lượng nước kèm sẽ khác nhau với vận tốc giảm do việc tách dòng chảy phía sau ống. Sự thay đổi này có thể được bỏ qua khi tính toán Ks. Tuy nhiên cần lưu ý rằng sự thay đổi trong lượng khối thủy động lực học (khối lượng nước kèm) sẽ ảnh hưởng đến tần số đáp ứng của các phần tử.
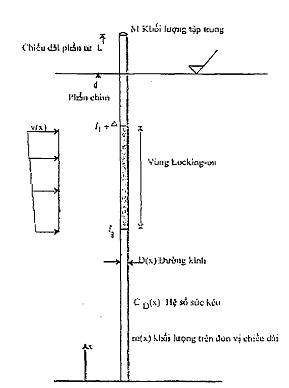
Hình 44 - Định nghĩa các thông số
12.1.12 Biến khối lượng nước kèm
Các khối lượng nước kèm thay đổi theo vận tốc giảm do việc tách dòng chảy sau ống, xem Hình 45. Sự biến động về khối lượng nước kèm sẽ ảnh hưởng đến tần số đáp ứng của các phần tử.
Hình 45 - Biến đổi khối lượng nước kèm với tốc độ giảm thu được từ sự dao động cưỡng bức và thử dao động tự do
12.2.1 Quy định chung
12.2.1.1 Dao động do dòng xoáy gây ra (VIO) có thể là một vấn đề thiết kế (cả ALS/ULS và FLS) đối với một loạt các đối tượng như: cầu, thượng tầng, kết cấu nổi, chân đế, ống đứng, cáp điều khiển và đường ống tiếp xúc gió, dòng chảy và/hoặc sóng. Các nguyên tắc cơ bản cho dự đoán của VIO là như nhau cho dòng chảy chất lỏng và các đối tượng khác nhau, tuy nhiên, một số điều kiện đặc biệt có thể áp dụng. Chuyển động thân cứng do dòng xoáy cảm ứng thường được gọi là chuyển động gây ra do dòng xoáy (VIM), trong khi xoáy gây ra rung chuyển động đàn hồi thường được gọi là (VIV).
12.2.1.2 Các ảnh hưởng quan trọng của VIV trên các phần tử mảnh là:
- Hệ thống có thể bị tổn thương mỏi đáng kể do VIV.
- VIV có thể làm tăng giá trị trung bình hệ số cản của các phần tử, ảnh hưởng đến phân tích tổng thể của các phần tử và có thể can thiệp tới các phần tử khác.
- VIV có thể ảnh hưởng dao động đánh thức cảm ứng (WIO) của mảng hình trụ. Tham khảo DNV-RP-F203
- VIV có thể góp phần đáng kể vào vận tốc va chạm tương đối của hai trụ cạnh nhau.
12.2.1.3 Hướng dẫn cụ thể cho các ống đứng và đường ống dẫn có thể được tìm thấy trong: DNV-RP-F204, DNV-RP-F203 và DNV-RP-F105
12.2.2 Khuếch đại kéo do VIV
12.2.2.1 Khuếch đại kéo do VIV phải được tính toán. Khuếch đại kéo là quan trọng đối với các chuyển động của các phần tử và để có thể giao thoa giữa các hình trụ trong hệ thống hình trụ. Một số biểu hiện cho sự gia tăng hệ số cản với rung tồn tại trong tài liệu, dựa trên biên độ A ước VIV chuẩn hóa bằng đường kính D. Một công thức đơn giản áp dụng cho hình trụ cố định:
|
| (292) |
trong đó:
A biên độ dao động dòng chảy chéo
CDo hệ số cản cho hình trụ tĩnh
D đường kính phần tử thanh
12.2.2.2 Giá trị đúng tương ứng với thí nghiệm về VIV các ống đứng được cho trong các biểu thức sau đây:
|
| (293) |
trong đó Anns là căn quân phương của biên độ VIV. Đối với chuyển động hình sin.
|
| (294) |
12.2.2.3 Sự kéo khuếch đại trong dòng sóng chiếm ưu thế là nhỏ hơn so với trong điều kiện dòng chảy thuần. Kéo khuếch đại trong sóng có thể được tính như sau:
|
| (295) |
12.3.1 Quy định chung
12.3.1.1 Gió gây ra rung của ống có thể xảy ra giữa hai mặt phẳng, thẳng trục hoặc vuông góc (cross-flow) với hướng gió.
12.3.2 Rung dọc trục
12.3.2.1 Rung dọc trục có thể xảy ra khi:
|
| (296) |
Rung dọc trục chỉ có thể xảy ra đối với các thông số ổn định nhỏ, ví dụ: Ks < 2.
12.3.3 Rung do dòng cắt ngang
12.3.3.1 Rung do dòng cắt ngang có thể xảy ra khi:
|
| (297) |
VR Uw / (fnD) là vận tốc giảm
St số Strouhal
Uw vận tốc gióc (m/s)
fn tần số dao động riêng của phần tử (1/s)
D đặc trưng kích thước mặt cắt ngang (m)
12.3.3.2 Các biên độ là một chức năng củs Ks cho các dao động dòng chảy xuyên phát triển đầy đủ có thể được tìm thấy từ Hình 46. Các thông số chế độ hình dạng, γ được sử dụng trong Hình này được định nghĩa là (xem Bảng 15 cho các giá trị hình điển):
|
| (298) |
Trong đó:
y(x) dạng hình học
ymax giá trị tối đa của dạng hình học
L chiều dài của phần tử
12.3.3.3 Đối với luồng gió mạnh đầy biến động, biên độ đưa ra là bảo toàn.
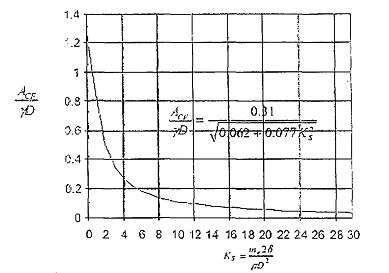
Hình 46 - Biên độ của chuyển động dòng chảy cắt ngang là hàm của Ks
Bảng 15 - Các thông số dạng hình dạng của một số phần tử kết cấu điển hình
| Phần tử kết cấu | γ |
| Trụ cứng | 1,00 |
| Cần quay | 1,29 |
| Chuỗi và cáp | 1,16 |
| Dầm đỡ đơn giản | 1,16 |
| Cantilever, dạng thứ nhất | 1,31 |
| Cantilever, dạng thứ hai | 1,50 |
| Cantilever, dạng thứ ba | 1,56 |
| Kẹp - kẹp, dạng thứ nhất | 1,17 |
| Kẹp - kẹp, dạng thứ hai | 1,16 |
| Kẹp - chốt, dạng thứ nhất | 1,16 |
| Kẹp - chốt, dạng thứ hai | 1,19 |
12.3.3.4 Các lực do dao động dòng chảy ngang kích thích vào một hình trụ tĩnh có thể được thể hiện bằng hệ số một lực nâng cắt CL:
|
| (299) |
Trong đó:
ρa Khối lượng riêng của không khí (kg/m3)
CL Hệ số nâng
12.3.4 Rung do xoáy gây ra của các phần tử trong kết cấu khung không gian
12.3.4.1 Các vấn đề của gió gây ra VIV của các phần tử trong gian các kết cấu khung không ngoài khơi phải được coi là một loại on-off. Hoặc là các phần tử sẽ được thử rung động cho vấn đề mỏi hoặc không thử rung động tránh nguy cơ rạn nứt do mỏi.
12.3.4.2 Phần tử này do đó cần được thiết kế theo một tiêu chí tránh mà xác định rằng cấu kết sẽ không rung.
12.3.4.3 Giả định rằng rung do dòng cắt ngang chỉ xảy ra trong mặt phẳng được xác định bởi các phần tử và vuông góc với hướng gió. Người ta phải cho phép khả năng mà gió có thể tới ở một góc ± 15 độ so với mặt phẳng nằm ngang.
12.3.4.4 Giới hạn dưới cho vận tốc gió gây rung dòng cắt ngang của các phần tử được đưa ra bởi sự giảm tốc độ:
|
| (300) |
Hoặc số hạng tương đương của vận tốc gió cực hạn:
|
| (301) |
trong đó:
St số Strouhal
fn Tần số dao động riêng của phần tử (1/s)
D Đặc trưng kích thước mặt cắt ngang (m)
12.3.4.5 Các phần tử của một kết cấu khung không gian có thể được giả định là không có rủi ro để gió gây ra VIV nếu
| U1year,1min (z) < U*w | (302) |
Trong đó:
U1year,1min (z) = 1 phút có nghĩa là tốc độ ở vị trí z của các phần tử với thời gian lặp lại 1 năm.
12.3.4.6 Khi vận tốc gió 1 năm được xác định trên vượt U*, các phần tử vẫn có thể được giả định là không có rủi ro cho VIV nếu các tiêu chí sau đây về số Reynolds và Ks là thỏa mãn:
![]()
![]()
Trong đó:
|
| (303) |
Số Reynolds tại vận tốc gió ![]() .
.
Đối với thép hình ống thông số ổn định được đưa ra bởi
|
| (304) |
Trong đó
ρs mật độ thép (kg/m3)
ρ mật độ không khí (1,25 kg/m3 ở 10 ° C) (kg/m3)
δ cấu giảm xóc δ = 2pz trong đó z = 0,0015
D đường kính phần tử (m)
t độ dày (m)
12.4 Dòng chảy gây ra dòng xoáy cảm ứng
12.4.1 Quy định chung
12.4.1.1 Trong các mô hình phản ứng dọc trục và rung dòng chảy được xem xét riêng biệt. Các mô hình đáp ứng được mô tả ở đây chủ yếu dành cho các tình huống lock-in đơn giản. Tuy nhiên sự thay đổi áp dụng khi có phản ứng ở một số chế độ có thể xảy ra cũng được trình bày.
12.4.1.2 Các mô hình đáp ứng được phát triển cho các điều kiện dòng chảy đồng nhất. Đối với dòng chảy cắt mạnh, hoặc dòng trong đó chỉ các bộ phận của các phần tử thanh phải chịu tác động dòng chảy, một lực mô hình được khuyến khích sử dụng trong đó biến không gian của kích thích và sức cản được được tính đến.
12.4.1.3 Đối với phản ứng ở chế độ cao trong đồng nhất hoặc dòng chảy cắt yếu, tham khảo Tiêu chuẩn DNV-RP-F204.
12.4.1.4 Trong tình huống Trong đó các phần tử được đặt trong dòng chảy cắt và trong khu vực lock-in một tần số xoáy thường sẽ chiếm ưu thế và tần số khác đang bị yếu thế trong khu vực chồng lấn.
12.4.1.5 Các xoáy cảm ứng có thể được xem xét cho phản ứng của các cell. Một biện pháp thống kê cho chiều dài của cell là tương quan giữa các lực cho các bộ phận ở chiều dài khác nhau. Điều này được xây dựng bởi chiều dài tương quan, lc:
|
| (305) |
|
| (306) |
12.4.1.6 Trong một vách ngăn có dòng xoáy các lực ngang Fcell có thể được xác định bằng
|
| (307) |
trong đó Cf @ 0,9. Cf sẽ luôn luôn được gán giá trị này không phân biệt số Reynolds.
12.4.1.7 Đối với một ống dài trong đó chiều dài tương quan là nhỏ so với chiều dài, A, qua đó điều kiện lock-in được thỏa mãn, tức là (lc << ∆) thiếu sự sửa đổi tương đối các lực trung bình mỗi đơn vị chiều dài F để được
|
| (308) |
Với lc > ∆, (lc / ∆) ≈ 1
Các biểu thức trên là các lực trên một hình trụ cố định.
12.4.2 Nhiều trụ và bó ống
12.4.2.1 Nhiều trụ và bó ống có thể thử nghiệm dòng xoáy cảm ứng như dòng xoáy cảm ứng tổng thể (trên tổng khối lượng kèm theo) hoặc như dòng xoáy cảm ứng cục bộ về phần tử riêng biệt.
12.4.2.2 Khi đường ống được cách nhau đều đặn dòng xoáy cảm ứng sẽ được xem tác động cục bộ vào mỗi phần tử. Tuy nhiên, khi các đường ống được cách nhau quá gần mà các hệ số cản cho tổng khối lượng kèm vượt quá 0,7, tổng số bó ống có thể được tiếp xúc với dòng xoáy cảm ứng tổng thể.
12.4.2.3 Các dòng xoáy cảm ứng kích thích sẽ phát triển với hệ số cản tổng thể trên bó. Đối với một bó ống tròn dòng xoáy cảm ứng kích thích sẽ được giống như đối với một hình rắn trụ tròn khi hệ số cản tổng thể lên bó ống tăng lên trên 1,2. Trong trường hợp này Cf = Cf0 có thể được sử dụng. Đối với hệ số cản tổng thể lên bó ống CD < 1,2, như được xác định trong 9, hệ số Cf sẽ phụ thuộc vào hệ số cản tổng thể:
|
| (309) |
trong đó Cf0 là hệ số dòng chảy ngang cho các thân kèm theo nếu nó là chất rắn. Ngoài ra có thể có xoáy cục bộ với phần tử riêng biệt.
12.4.2.4 Ống cách nhau do đó hệ số cản cho tổng khối lượng kèm theo là dưới 0,7 sẽ chỉ được tiếp xúc với xoáy cảm ứng cục bộ với các phần tử.
12.4.3 Mô hình phản ứng VIV dọc trục
12.4.3.1 VIV dọc trục được tách thành chuyển động trong dòng đơn thuần và chuyển động dòng chảy chéo gây ra trong dòng.
12.4.3.2 Cộng hưởng dòng xoáy cảm ứng trong dòng đơn thuần (lock-in) có thể xảy ra khi:
| 1,0 < VR < 4,5 | (310) |
| KS ≤ 1,8 | (311) |
Tùy thuộc vào vận tốc dòng chảy xoáy hoặc là được tác động đối xứng hay cách khác từ hai bên của hình trụ.
12.4.3.3 Đối với 1,0 < VR < 2,2, tại khu vực bất ổn đầu tiên, sự tác động sẽ là đối xứng. Các tiêu chí cho sự khởi đầu của sự chuyển động trong khu vực bất ổn đầu tiên được đưa ra trong Hình 48. Các tiêu chí bắt đầu chỉ có giá trị khi vận tốc giảm VR ngày càng tăng. Trong dòng chảy không ổn định VR có thể đi từ giá trị cao đến giá trị thấp rung lock-in sẽ tồn tại với tất cả các giá trị VR ≥ 1,0.
12.4.3.4 Đối với VR > 2,2 đổ sẽ không đối xứng, chuyển động sẽ diễn ra ở khu vực thứ hai ổn định (2,2 < VR < 4,5) cho KS < 1,8. Tiêu chuẩn để kết thúc chuyển động trong khu vực bất ổn thứ hai được cho trong Hình 48.
12.4.3.5 Các biên độ tối đa của các dao động tương đối so với đường kính được xác định là một chức năng của tham số ổn định KS, xem Hình 47. Trong trường hợp đường kính khác nhau, đường kính trung bình của khu vực lock-in có thể được sử dụng.
Đối với các dự báo chi tiết hơn về biên độ phản ứng IL, tham khảo DNV-RP-F105.
12.4.3.6 VIV gây ra do dòng chảy chéo trong dòng là liên quan các giá trị vận tốc giảm trong đó VIV gây ra do dòng chảy chéo xảy ra. VIV gây ra do dòng chảy chéo trong dòng có thể được ước tính bằng cách:
- Các chế độ IL với tần số riêng của nó gần gấp đôi (chi phối) tần số đáp ứng CF được chọn là ứng cử viên cho các CF gây ra IL.
- Biên độ được tính như là 40% biên độ CF.
Hình 47 - Biên độ của chuyển động trong dây chuyền như một chức năng của KS
Hinh 48 - Tiêu chí cho bắt đầu của chuyển vị trong khu vực bất ổn nội tuyến đầu tiên (1,0 < VR < 2,2) và kết thúc vùng bất ổn thứ hai
12.4.4 Mô hình phản ứng VIV dòng vuông góc
12.4.4.1 Sự kích thích dòng xoáy cảm ứng dòng vuông góc có thể xảy ra khi:
| 3 ≤ VR ≤ 16 | (312) |
Đối với toàn bộ số Reynolds, và Phản ứng tối đa thường được tìm thấy trong khoảng 5 ≤ VR ≤ 9
12.4.4.2 Các biên độ tối đa của các dao động dòng chảy chéo tương ứng với đường kính D và dạng mode γ có thể được xác định từ Hình 46. Trong trường hợp đường kính khác nhau, đường kính trung bình của khu vực lock-in có thể được sử dụng.
12.4.4.3 Một mô hình phản ứng chi tiết hơn trong dòng chảy ổn định thống nhất được trình bày như sau: Các phản ứng biên độ (AID) như là một hàm của vận tốc giảm VR có thể được xây dựng từ:
|
|
| (313) |
12.4.4.4 Biên độ phản ứng dòng vuông góc tối đa 1,3D chỉ áp dụng cho các mô hình thân cứng của hình trụ được gá mềm hoặc ở dạng uốn đối xứng đầu tiên của các phần tử mềm, và cho phản ứng với mô hình đơn. Đối với các trường hợp khác, biên độ phản ứng tối đa được giới hạn 0,9D.
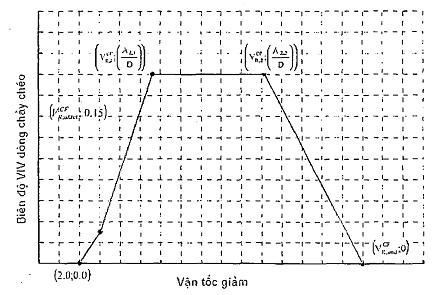
Hình 49 - Nguyên lý mô hình phản ứng
12.4.4.5 Các phản ứng biên độ đặc trưng cho VIV dòng chảy chéo như được đưa ra ở trên có thể bị giảm do sự ảnh hưởng của giảm xóc:
|
| (314) |
trong đó Hệ số giảm Rk được đưa ra bởi:
|
| (315) |
Độ lệch chuẩn tương ứng có thể thu được từ:
|
| (316) |
12.5 Xoáy cảm ứng do sóng gây ra
12.5.1 Quy định chung
12.5.1.1 Các chuyển động quỹ đạo trong sóng có thể tạo ra dòng xoáy cảm ứng về thành phần cấu trúc.
12.5.1.2 Tỷ lệ vận tốc dòng chảy được định nghĩa là:
|
| (317) |
Nếu α > 0.8, dòng chảy được dòng chảy chiếm ưu thế.
12.5.1.3 Số Keulegan-Carpenter KC được định nghĩa là:
|
| (318) |
Trong đó:
vm vận tốc quỹ đạo tối đa do sóng chuyển động vuông góc với trục phần tử có hình trụ tĩnh.
T chu kỳ sóng
Số KC là một hàm của chiều sâu. Sự thay đổi này sẽ được xem xét trong tính toán.
12.5.1.4 Trong dòng chảy bất thường số KC có thể được tính bằng cách thay vm với "vận tốc chất lỏng đáng kể". Dựa trên các thông số trạng thái biển, vận tốc đáng kể trong nước sâu có thể được ước tính như sau:
|
| (319) |
Trong đó:
HS chiều cao đáng kể sóng:
Tp chu kỳ đỉnh sóng;
kp số sóng tương ứng với một sóng với thời gian Tp;
z trục dọc hướng lên dương, có nghĩa là bề mặt tự do là tại z = 0.
12.5.1.5 Ngoài ra, vận tốc đáng kể có thể được tính như:
|
| (320) |
trong đó vrms là độ lệch chuẩn của vận tốc quỹ đạo do sóng chuyển động vuông góc với trục phần tử hình trụ tĩnh.
12.5.1.6 Các dòng xoáy cảm ứng trong sóng rơi vào hai loại phụ thuộc vào số lượng Keulegan- Carpenter, KC:
a) Dòng xoáy cảm ứng cùng loại như trong dòng chảy ổn định, loại này tồn tại cho KC > 40.
b) Dòng xoáy cảm ứng cho 6 < KC < 40. Trong phạm vi này tần số dòng xoáy cảm ứng sẽ được xác định bởi các loại chuyển động sóng.
12.5.2 Sóng chuyển động thường xuyên và không thường xuyên
12.5.2.1 Đối với chuyển động sóng thường xuyên, một loại cộng hưởng giữa sóng và dòng xoáy cảm ứng diễn ra. Các tần số dòng xoáy cảm ứng sẽ là một bội số của tần số sóng. Số dòng xoáy cảm ứng dao động mỗi chu kỳ sóng, N, đang chuyển động sóng thường xuyên được cho bởi:
|
| KC | N |
|
|
| 7 ÷ 15 | 2 |
|
|
| 15 ÷ 24 | 3 |
|
|
| 24 ÷ 32 | 4 |
|
|
| 32 ÷ 40 | 5 |
|
12.5.2.2 Sức mạnh của các lực ngang được tăng tại các điều kiện cộng hưởng. Hệ số dòng xoáy cảm ứng Cf được sửa đổi như trong Hình 51.
12.5.3 Dòng xoáy cảm ứng cho Keulegan-Carpenter số > 40
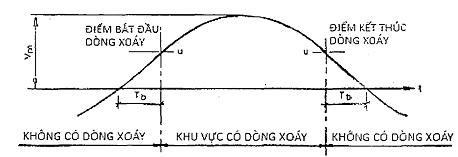
Hình 50 - Tiêu chí cho sự hiện diện của xoáy đổ trong sóng
12.5.4 Dòng xoáy cảm ứng cho số Keulegan-Carpenter < 40
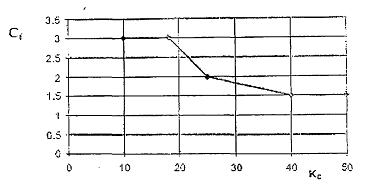
Hình 51 - Hệ số nâng Cf là hàm của số KC
13 Thử mô hình thủy động lực học
13.1.1 Quy định chung
13.1.1.1 Thử mô hình quy mô nhỏ là một công cụ cũng được thành lập để xác nhận các mô hình thủy động lực học và khi động học lý thuyết, ước lượng hệ số liên quan, cũng như trong việc xác minh thiết kế mới hoặc sửa đổi kết cấu ngoài biển.
13.1.1.2 Tiêu chuẩn này đưa ra hướng dẫn chung khi thực hiện các cuộc thử mô hình, và trên nguyên tắc quy trình. Sự cần thiết phải thử mô hình phụ thuộc vào vấn đề và mục đích thực tế, và phải được đánh giá trong từng tình huống cụ thể.
13.1.2 Các loại và mục đích chung của mô hình thử
13.1.2.1 Thử mô hình thủy động lực học quy mô nhỏ có thể được tạm phân thành bốn loại chung sau đây:
- Xác định hệ số thủy động lực cho các phần tử kết cấu độc lập
- Nghiên cứu của Tong hành vi hệ thống
- Xác nhận các mô hình số mới
- Kiểm tra hoạt động hàng hải và chứng minh chức năng hoặc các ảnh hưởng đặc biệt.
13.1.2.2 Thử mô hình thủy động lực học nên được thực hiện để:
- Xác nhận rằng không có hoạt động thủy động lực quan trọng nào đã bị bỏ qua
- Hỗ trợ tính toán lý thuyết khi các phương pháp phân tích có sẵn có thể sai sót
- Xác minh phương pháp lý thuyết trên cơ sở chung.
13.1.3 Tải trọng và phản ứng cực hạn
13.1.3.1 Đối với vấn đề phi tuyến mạnh, mô hình thử có thể được sử dụng để ước tính tải trọng hạn cực và phản ứng cực hạn. Ước lượng như vậy đòi hỏi một đánh giá được chứng nhận của cực hạn tương ứng để đưa ra chu kỳ lặp.
13.1.4 Phương pháp và quy trình thử
13.1.4.1 Tiêu chuẩn này tập trung vào các nguyên tắc cơ bản để thử mô hình, không phải trên các chi tiết trong các thiết lập.
13.2 Khi nào được đề nghị mô hình thử
13.2.1 Quy định chung
13.2.1.1 Khi một tình huống thử mô hình được đưa ra, một số trong số các hạng mục sau đây được tính đến:
- Đặc trưng tải trọng thủy động lực
- Khái niệm hệ thống tổng thể và thẩm định thiết kế
- Thử thành phần kết cấu riêng biệt
- Hoạt động hàng hải
- Xác thực của mô hình số
- Ước tính tải trọng và phản ứng cực hạn.
13.2.1.2 Thử mẫu rất quan trọng để kiểm tra xem tất cả các hiện tượng cần thiết đã được đưa vào phân tích số liệu hay không. Hiện tượng không rõ hoặc không mong muốn thường có thể xảy ra trong quá trình thử mô hình.
13.2.2 Hệ thống khái niệm tổng thể và thẩm tra thiết kế
13.2.2.1 Đối với một hệ thống kết cấu hoàn thiện, nghĩa là một trong hai kết cấu cố định từ nền móng hoặc kết cấu nổi thả neo với dây neo và các ống đứng, kiểm tra mô hình được thực hiện để xác minh kết quả từ Tong phân tích. Điều này được thực hiện với thiết kế cuối cùng nhưng là hữu ích cũng trong giai đoạn khái niệm. Các thông số được kiểm chứng bằng thực nghiệm hoặc kiểm tra với nhiều loại hình kết cấu được đưa ra dưới đây.
13.2.2.2 Kết cấu cố định: Đối với các giàn jacket, kiểm tra mô hình cung cấp các lực tác động sóng sàn tổng thể và cục bộ.
13.2.3 Thử thành phần kết cấu đơn lẻ
Thử mô hình thường được thực hiện để nghiên cứu chi tiết từng phần của cấu kết. Đây là những thí nghiệm điển hình cơ bản hơn, với mục đích để có được kiến thức tổng quát về các thông số như mô tả trong 13.2.2.
13.2.4 Hiệu lực của mô hình số phi tuyến
13.2.4.1 Sự phát triển của quy phạm và các mô hình phi tuyến mới yêu cầu hiệu lực bằng thực nghiệm. Điều này là đúng cho tất cả các mô hình, ví dụ: Động lực Học Chất Lỏng (CFD) và sự mô phỏng của sóng bất thường phi tuyến.
13.2.4.2 Hiệu lực của công cụ hoàn toàn phi tuyến và CFD: Sự phát triển mạnh mẽ của các công cụ phi tuyến mới và CFD đòi hỏi những nỗ lực đáng kể trong thử nghiệm thực tiễn, cùng với điểm chuẩn so với các công cụ lý thuyết và số khác. Thí nghiệm như vậy cần kế hoạch cẩn thận và quy trình hợp lý.
13.2.4.3 Hiệu lực của mô hình sóng bất thường phi tuyến: Các mô tả bằng lý thuyết và bằng số hóa của sóng ngẫu nhiên dốc phi tuyến chưa hoàn chỉnh, đặc biệt là không trong vùng biển bất thường và trong nước nông. Các hạng mục cụ thể bao gồm;
- Dự đoán của chiều cao sóng và đỉnh cực hạn các trong vùng biển bất thường;
- Thống kê không Gaus;
- Động học tại vùng dao động sóng trong vùng biển;
- Ảnh hưởng nước nông;
- Thay đổi của động học sóng do một dòng chảy trung bình.
13.2.5 Tải và phản ứng cực hạn
Để xác minh tải thiết kế, thử mô hình trong bão ở các trạng thái biển với sóng bất thường thực tế là cần thiết để tính đến các giá trị phi tuyến có liên quan trong sóng cũng như trong tương tác sóng-kết cấu. Công cụ phân tích phải được hiệu chuẩn trong các trường hợp khác nhau. Điều này áp dụng đối với các thông số như xê dịch trôi dạt chậm cực hạn; tải neo đậu; lực tác động trong sóng hạn cực.
13.3 Giới hạn và đơn giản hóa trong mô hình vật lý
13.3.1.1 Với mục đích thực sự của thử mô hình thí nghiệm, phải lập kế hoạch và thực hiện các cuộc thử theo một cách tối ưu cho mục đích đó. Các chi tiết không quan trọng được bỏ qua. Điều này được quyết định từ một điểm lực thủy động lực học trong hiển thị, và trong một số trường hợp có yêu cầu bổ sung từ một điểm hiển thị của màn hình (ghi hình). Sự quan trọng có thể khác nhau giữa các loại thí nghiệm khác nhau. Ngoài ra còn có những hạn chế cơ bản và thực tiễn trong mô hình thí nghiệm quy mô nhỏ cần được đưa ra để tính toán.
13.4 Thiết lập hiệu chuẩn mô hình vật lý
Các mô hình và thiết lập của nó phải được kiểm tra và hiệu chuẩn.
13.4.1 Các mô hình có đáy cố định
Đối với mô hình cố định, cứng các mục sau đây phải được hiệu chuẩn / kiểm tra:
- Đặc điểm mô hình (hình học);
- Độ cứng tổng thể của mô hình đã cài đặt, đặc biệt là khi các mô hình có chu kỳ dao động riêng thấp;
- Kiểm tra các thiết bị đo đạc; đặc điểm cảm biến; mức độ chính xác.
Đối với mô hình đàn hồi hoặc chuyển tiếp, sự phân bố khối lượng và độ cứng cũng quan trọng.
13.5.1 Quy định chung
13.5.1.1 Cách phổ biến nhất để mở rộng mô hình là sử dụng luật Froude rộng (xem Bảng 16) dựa trên các ảnh hưởng của gia tốc trọng trường, và tỷ lệ chia được định nghĩa bởi số Froude. Nó thường được áp dụng cho các lực thủy động lực chính trong tàu và giàn hình điển.
13.5.2 Vấn đề nhớt
13.5.2.1 Khi lực nhớt là đáng kể, số Reynolds cũng có liên quan do tác động dòng xoáy cảm ứng, và các hiệu chỉnh cho tỷ xích Froude có thể cần thiết. Các hiệu chỉnh như vậy thường được gọi là "các ảnh hưởng tỷ xích". Về nguyên tắc cũng có thể căn cứ vào tỷ lệ hoàn thiện vào số Reynolds thay vì số Froude, nhưng không thường được thực hiện. Các ảnh hưởng do các túi khí và các hiện tượng chi phối bởi sức căng bề mặt như sóng vỡ, cũng có tỷ lệ khác nhau tiệm cận Froude.
Bảng 16 - Luật chia Froude
| Thông số | Hệ số chia | Đơn vị mẫu (điển hình) | Đơn vị tỷ lệ thực (điển hình) |
| Chiều dài | λ | m | m |
| Vận tốc | λ1/2 | m/s | m/s |
| Gia tốc dài | λ0 | m/s2 | m/s2 |
| Gia tốc góc | λ-1 | độ/s2 | độ/s2 |
| Góc | λ0 | độ | độ |
| Lực | λ31,026 | N | kN |
| Moment | λ41,026 | Nm | kNm |
| Thời gian | λ1/2 | s | s |
13.5.3 Lựa chọn tỷ xích
13.5.3.1 Tỷ xích mô hình cần được đủ lớn để đảm bảo rằng:
- Lực thủy động lực học và các hiện tượng là quan trọng đối với kết quả kiểm tra được mô phỏng một cách chính xác,
- Tỷ xích của các kết quả có thể được thực hiện dựa trên luật mô hình đã được chứng minh và tương quan dữ liệu thực nghiệm,
- Quy mô mô hình là đầy đủ đối với các thử khoang chứa và thử hệ thống công nghệ, cũng như khả năng phát sinh của các điều kiện môi trường,
- Độ chính xác đo đạc chấp nhận được có thể đạt được.
13.5.3.2 Lựa chọn tỷ xích có thể là một sự thỏa hiệp giữa các yêu cầu trên. Những lý do cho tỷ xích đề xuất cần được nêu rõ.
13.5.3.3 Trong thực tế, tỷ xích điển hình được chọn giữa 1:30 và 1: 100. Tỷ xích lớn hơn được giới hạn bởi kích thước phòng thí nghiệm và thực tiễn hoặc cân nhắc kinh tế, trong khi tỷ xích nhỏ thường ít khi được sử dụng - chủ yếu là do không chắc chắn tăng và ít lặp lại trong các mô hình, và cũng do ảnh hưởng tỷ xích.
13.5.4 Tỷ lệ chia đối với đo tải trọng va đập sóng
13.5.4.1 Áp lực va đập sóng và áp lực nước được thu nhỏ theo luật nhân rộng của Froude. Ảnh hưởng tỷ xích trên những áp lực do đó chủ yếu liên quan đến hàm lượng không khí trong nước, độ rỗng không khí đã được chứng minh là làm giảm áp lực tác động tối đa và tăng thời gian tăng tham khảo Bullock, et. al. (2001) Do khác nhau về thể chất, hóa học và sinh học của nước ngọt và nước biển, các bong bóng hình thành trong nước ngọt có xu hướng lớn hơn so với những hình trong nước biển và họ kết hợp lại một cách dễ dàng hơn. Do đó, không khí có thể thoát ra nhanh chóng hơn từ nước ngọt từ nước biển hơn. Vì vậy, tỷ xích của luật Froude của đỉnh áp suất đo được.
13.5.4.2 Trong trường hợp khí then kẹt, các vảy đỉnh áp lực với căn bậc hai của các tỷ lệ chia trong khi cho rộng Froude của, các vảy đỉnh áp lực với tỷ lệ chia.
13.5.5 Các ảnh hưởng khác
13.5.5.1 Sức căng bề mặt chất lỏng tự do không chia tỷ lệ theo luật Froude, và phải được xử lý cẩn thận. Nó xác định một giới hạn chia thấp hơn cơ bản cho mô hình sóng trọng lực, nhưng thường không ảnh hưởng đến tỷ lệ chia lớn hơn khoảng 1:200.
13.5.5.2 Ứng suất, sức căng và đàn hồi kết cấu của một quá trình liên tục không thể quan sát trực tiếp từ các cuộc thử mô hình, và nếu nó phải được bao gồm trong các thử nghiệm nó phải được xử lý theo mô hình của ví dụ nút giao rời rạc tại đó monent cục bộ được đo.
Bảng A-1: Hệ số nước kèm đối với các dạng thân hai chiều, như các trụ dài, khối lượng nước kèm (trên đơn vị dài) là mA = ρCAAR, trong đó AR là diện tích tham chiếu
| Dạng tiết diện | Hướng chuyển động | CA | AR | Mô men quán tính nước kèm | |||||
|
|
| 1,0 | pa2 | 0 | |||||
|
| Đứng | 1,0 | pa2 |
| |||||
| Ngang | 1,0 | pa2 | |||||||
|
| Đứng | 1,0 | pa2 |
| |||||
|
| Đứng | 1,0 | pa2 |
Trong đó:
Và
p / 2 < α < p | |||||
| Ngang |
| pa2 | |||||||
|
| Ngang hoặc Đứng | 1,0 | pa2 |
| |||||
|
| a/b = ∞ | Đứng | 1,10 | pa2 | β1ρpa4 hay β2ρpb4 | ||||
| a/b = 10 | 1,14 | a/b | β1 | β2 | |||||
| a/b = 5 | 1,21 | 0,1 | - | 0,147 | |||||
| a/b = 2 | 1,36 | 0,2 | - | 0,15 | |||||
| a/b = 1 | 1,51 | 0,5 | - | 0,15 | |||||
| a/b = 0,5 | 1,70 | 1,0 | 0,234 | 0,234 | |||||
| a/b = 0,2 | 1,98 | 2,0 | 0,15 | - | |||||
| a/b = 0,1 | 2,23 | 5,0 | 0,15 | - | |||||
|
|
| ∞ | 0,125 | - | |||||
|
| d/a = 0,05 | Đứng | 1,61 | pa2 | βρpa4 | ||||
| d/a = 0,10 | 1,72 | d / a | β | ||||||
| d/a = 0,25 | 2,19 | 0,05 | 0,31 | ||||||
|
|
| 0,10 | 0,40 | ||||||
|
|
| 0,10 | 0,69 | ||||||
|
| a/b = 2 | Đứng | 0,85 | pa2 | 0,059 ρpa4 chỉ khi a = b | ||||
| a/b = 1 | 0,76 | ||||||||
| a/b = 0,5 | 0,67 | ||||||||
| a/b = 0,2 | 0,61 | ||||||||
|
| Mọi hướng |
| pa2 |
| |||||
|
| Đứng |
|
|
| |||||
|
| Ngang | d/a = ∞ | 1,000 | pa2 |
| ||||
| d/a = 1,2 | 1,024 | ||||||||
| d/a = 0,8 | 1,044 | ||||||||
| d/a = 0,4 | 1,096 | ||||||||
| d/a = 0,2 | 1,160 | ||||||||
| d/a = 0,1 | 1,224 | ||||||||
|
|
|
| |||||||
|
|
Có giá trị khi chu kỳ dao động dài | 2ρc2 |
| ||||||
Bảng A-2: Hệ số khối lượng nước kèm đối với dạng thân ba chiều trong chất lỏng vô hạn. Khối lượng nước kèm là mA = ρCAVR, trong đó VR là thể tích tham chiếu
| Dạng | Hướng chuyển động | CA | VR | ||||||
| Tấm phẳng |
| Đứng | 2 / p |
| |||||
|
| Đứng | b / a | CA | b / a | CA |
| |||
| ∞ | 1,000 | 5,0 | 0,952 | ||||||
| 14,3 | 0,991 | 4,0 | 0,933 | ||||||
| 12,8 | 0,989 | 3,0 | 0,900 | ||||||
| 10,0 | 0,984 | 2,0 | 0,826 | ||||||
| 7,0 | 0,972 | 1,5 | 0,758 | ||||||
| 6,0 | 0,964 | 1,0 | 0,637 | ||||||
|
| Đứng | b / a | CA | b / a | CA |
| |||
| 1,00 | 0,579 | 3,17 | 0,840 | ||||||
| 1,25 | 0,642 | 4,00 | 0,872 | ||||||
| 1,50 | 0,690 | 5,00 | 0,897 | ||||||
| 1,59 | 0,704 | 6,25 | 0,917 | ||||||
| 2,00 | 0,757 | 8,00 | 0,934 | ||||||
| 2,50 | 0,801 | 10,00 | 0,947 | ||||||
| 3,00 | 0,830 | ∞ | 1,000 | ||||||
|
| Đứng |
|
| ||||||
| Thân dạng tròn |
| Mọi hướng |
|
| |||||
|
| Đứng hoặc ngang | a/b | CA |
| |||||
| 1,0 | Ngang | Đứng | |||||||
| 1,5 | 0,500 | 0,050 | |||||||
| 2,0 | 0,304 | 0,622 | |||||||
| 2,5 | 0,210 | 0,704 | |||||||
| 4,0 | 0,156 | 0,762 | |||||||
| 5,0 | 0,082 | 0,860 | |||||||
| 6,0 | 0,059 | 0,894 | |||||||
| 7,0 | 0,045 | 0,917 | |||||||
| 8,0 | 0,036 | 0,933 | |||||||
|
| 0,029 | 0,945 | |||||||
| Ê líp | Ngang a > b > c
| Ngang |
Trong đó:
ε = b / a δ = c / a |
| |||||
| Lăng trụ vuông |
| Đứng | b / a | CA | a2b | ||||
| 1,0 | 0,68 | ||||||||
| 2,0 | 0,36 | ||||||||
| 3,0 | 0,24 | ||||||||
| 4,0 | 0,19 | ||||||||
| 5,0 | 0,15 | ||||||||
| 6,0 | 0,13 | ||||||||
| 7,0 | 0,11 | ||||||||
| 10,0 | 0,08 | ||||||||
| Trụ tròn |
| Đứng | b / 2a | CA | pa2b | ||||
| 1,2 | 0,62 | ||||||||
| 2,5 | 0,78 | ||||||||
| 5,0 | 0,90 | ||||||||
| 9,0 | 0,96 | ||||||||
| ∞ | 1,00 | ||||||||
Bảng B: Hệ số cản lên tiết diện dạng không tròn đối với dòng chảy tĩnh CDS
| Dạng hình học | Hệ số cản CD | |||||||||||||
|
| Dạng (Re = 104 ~ 107) | CD | ||||||||||||
| Dây, 6 tao |
| |||||||||||||
| Dây, xoăn không vỏ bọc | 1,5 ~ 1,8 | |||||||||||||
| Dây, xoăn không vỏ bọc | 1,4 ~ 1,6 | |||||||||||||
| Dây, xoắn có vỏ bọc | 1,0 ~ 1,2 | |||||||||||||
| Xích, có mã stud (đường kính xích tương ứng) | 2,2 ~ 2,6 | |||||||||||||
| Xích, không mã stud (đường kính xích tương ứng) | 2,0 ~ 2,4 | |||||||||||||
|
| L/D | T/D | ||||||||||||
| 0 | 5 | 10 | ||||||||||||
| 0,1 | 1,9 | 1,4 | 1,38 | |||||||||||
| 0,2 | 2,1 | 1,4 | 1,43 | |||||||||||
| 0,4 | 2,35 | 1,39 | 1,46 | |||||||||||
| 0,6 | 1,8 | 1,38 | 1,48 | |||||||||||
| 0,8 | 2,3 | 1,36 | 1,47 | |||||||||||
| 1,0 | 2,0 | 1,33 | 1,45 | |||||||||||
| 1,5 | 1,8 | 1,30 | 1,40 | |||||||||||
| 2,0 | 1,6 | - | 1,33 | |||||||||||
| Re ~ 5 x 104 | ||||||||||||||
|
|
| |||||||||||||
| L/D | 0,1 | 0,25 | 0,50 | 1,0 | 2,0 | |||||||||
| n | 2,3 | 2,2 | 2,1 | 1,2 | 0,4 | |||||||||
| Re >103 | ||||||||||||||
|
| L/D | R/D | CD | L/D | R/D | CD | ||||||||
| 0,5 | 0 | 2,5 | 2,0 | 0 | 1,6 | |||||||||
|
| 0,021 | 2,2 |
| 0,042 | 1,4 | |||||||||
|
| 0,083 | 1,9 |
| 0,167 | 0,7 | |||||||||
|
| 0,250 | 1,6 |
| 0,50 | 0,4 | |||||||||
| 1,0 | 0 | 2,2 | 6,0 | 0 | 0,89 | |||||||||
|
| 0,021 | 2,0 |
| 0,5 | 0,29 | |||||||||
|
| 0,167 | 1,2 |
|
|
| |||||||||
|
| 0,333 | 1,0 |
|
|
| |||||||||
| Re ~ 105 | ||||||||||||||
|
| θ | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | |||||||
| CD | 2,2 | 2,1 | 1,8 | 1,3 | 1,9 | 2,1 | 2,2 | 2,3 | 2,4 | 2,4 | ||||||||
| Re ~ 4,7 x 104 | ||||||||||||||||||
|
| L0/D0 | R/D0 | CD |
| ||||||||||||||
| 0,5 | 0,021 | 1,8 | Góc trước và sau không tròn | |||||||||||||||
|
| 0,083 | 1,7 | ||||||||||||||||
|
| 0,167 | 1,7 | ||||||||||||||||
| 1,0 | 0,015 | 1,5 |
| |||||||||||||||
|
| 0,118 | 1,5 | ||||||||||||||||
|
| 0,235 | 1,5 | ||||||||||||||||
| 2,0 | 0,040 | 1,1 | Các góc bên không tròn | |||||||||||||||
|
| 0,167 | 1,1 | ||||||||||||||||
|
| 0,335 | 1,1 | ||||||||||||||||
| Re ~ 105 | ||||||||||||||||||
|
| L/D | CD | ||||||||||||||||
| 0,5 | 1,16 | |||||||||||||||||
| 1,0 | 0,90 | |||||||||||||||||
| 2,0 | 0,70 | |||||||||||||||||
| 4,0 | 0,68 | |||||||||||||||||
| 6,0 | 0,64 | |||||||||||||||||
|
| CD = 1,9 ; Re > 104 | |||||||||||||||||
|
|
CL = CN cosθ CD = CN sinθ | |||||||||||||||||
|
| CD ~ 0,01 CL = 2 p sinθ CL = (p/4) sin2θ (mô ment tại góc đầu) CM = 0 đối với điểm sau góc đầu | |||||||||||||||||
|
| E/D | CD | ||||||||||||||||
| 0,5 | 1,42 hoặc 2,20 | |||||||||||||||||
| 1,0 | 1,52 hoặc 2,13 | |||||||||||||||||
| 2,0 | 1,9 hoặc 2,10 | |||||||||||||||||
| 3,0 | 2,0 | |||||||||||||||||
| 5,0 | 1,96 | |||||||||||||||||
| 10,0 | 1,9 | |||||||||||||||||
| 15,0 | 1,9 | |||||||||||||||||
| Re ~ 4 x 103 | ||||||||||||||||||
|
| E/D | CD1 | CD2 | |||||||||||||||
| 2 | 1,80 | 0,10 | ||||||||||||||||
| 3 | 1,70 | 0,67 | ||||||||||||||||
| 4 | 1,65 | 0,76 | ||||||||||||||||
| 6 | 1,65 | 0,95 | ||||||||||||||||
| 10 | 1,9 | 1,00 | ||||||||||||||||
| 20 | 1,9 | 1,15 | ||||||||||||||||
| 30 | 1,9 | 1,33 | ||||||||||||||||
| ∞ | 1,9 | 1,90 | ||||||||||||||||
| Re ~ 4 x 103 | ||||||||||||||||||
|
|
Re > 103 | |||||||||||||||||
|
| D/L | CD(Re ~ 105) | ||||||||||||||||
| 0,125 | 0,22 | |||||||||||||||||
| 0,25 | 0,3 | |||||||||||||||||
| 0,50 | 0,6 | |||||||||||||||||
| 1,00 | 1.0 | |||||||||||||||||
| 2,0 | 1,6 | |||||||||||||||||
|
| θ | CD(Re ~ 104) | ||||||||||||||||
| 30 | 1,1 | |||||||||||||||||
| 60 | 1,4 | |||||||||||||||||
| 90 | 1,6 | |||||||||||||||||
| 120 | 1,75 | |||||||||||||||||
|
| θ | CD(Re = 104) | ||||||||||||||||
| 30 | 1,9 | |||||||||||||||||
| 60 | 2,1 | |||||||||||||||||
| 90 | 2,15 | |||||||||||||||||
| 120 | 2,05 | |||||||||||||||||
Bảng C: Khối lượng riêng và độ nhớt động học của nước, nước biển và không khí
| Nhiệt độ °C | Khối lượng riêng ρ kg/m3 | Độ nhớt động học v m2/s | ||||
| Nước | Nước biển | Không khí | Nước | Nước biển | Không khí | |
| 0 | 999,8 | 1028,0 | 1,293 | 1,79 x 10-6 | 1,83 x 10-6 | 1,32 x10-5 |
| 5 | 1000,0 | 1027,6 | 1,270 | 1,52 | 1,56 | 1,36 |
| 10 | 999,7 | 1026,9 | 1,247 | 1,31 | 1,35 | 1,41 |
| 15 | 999,1 | 1025,9 | 1,226 | 1,14 | 1,19 | 1,45 |
| 20 | 998,2 | 1024,7 | 1,205 | 1,00 | 1,05 | 1,50 |
| 25 | 997,0 | 1023,2 | 1,184 | 0,89 | 0,94 | 1,55 |
| 30 | 995,6 | 1021,7 | 1,165 | 0,80 | 0,85 | 1,60 |
1 Phạm vi áp dụng
2 Tài liệu viện dẫn
3 Chữ viết tắt
4 Quy định chung
4.1 Điều kiện môi trường
4.2 Tải trọng môi trường
5 Điều kiện gió
5.1 Quy định chung
5.1.1 Tổng quát
5.1.2 Các thông số gió
5.2 Dữ liệu gió
5.2.1 Thống kê tốc độ gió
5.3 Mô hình gió
5.3.1 Tốc độ gió trung bình
5.3.2 Profile tốc độ gió
5.3.3 Mô hình rối của tải trọng gió
5.3.4 Phổ gió
5.3.5 Quá trình tốc độ gió và vùng tốc độ gió
5.3.6 Đường biểu đồ gió và độ ổn định khí quyển
5.4 Điều kiện gió ngắn hạn
5.4.1 Quy định chung
5.4.2 Gió giật (Gusts)
5.4.3 Tố lốc (Squalls)
6 Điều kiện sóng
6.1 Quy định chung
6.1.1 Khái niệm
6.1.2 Đặc trưng chung của sóng
6.2 Các lý thuyết sóng điều hòa
6.2.1 Tính ứng dụng của các lý thuyết sóng
6.2.2 Lý thuyết sóng tuyến tính
6.2.3 Lý thuyết sóng Stokes
6.2.4 Lý thuyết sóng Cnoidal
6.2.5 Lý thuyết sóng đơn
6.2.6 Lý thuyết sóng hàm dòng
6.3 Động học sóng
6.3.1 Động học sóng điều hòa
6.3.2 Mô hình hóa sóng không điều hòa
6.3.3 Động học sóng không điều hòa
6.4 Sự biến dạng sóng
6.4.1 Quy định chung
6.4.2 Hiệu ứng nước nông (Shoaling)
6.4.3 Sự khúc xạ (Refraction)
6.4.4 Sự phản xạ sóng (Wave reflection)
6.4.5 Sóng đứng trong vịnh nước nông
6.4.6 Chiều cao sóng lớn nhất và sóng vỡ
6.5 Điều kiện sóng ngắn hạn
6.5.1 Quy định chung
6.5.2 Phổ sóng
6.5.3 Những thông số trạng thái biển
6.5.4 Độ dốc sóng
6.5.5 Phổ Pierson-Moskowitz và JONSWAP
6.5.6 Phổ TMA
6.5.7 Phổ 2 đỉnh
6.5.8 Phân phối hướng của gió biển và sóng lừng
6.5.9 Phân phối ngắn hạn của chiều cao sóng
6.5.10 Phân phối ngắn hạn của đỉnh sóng trên mực nước tĩnh
6.5.11 Chiều cao sóng lớn nhất và chiều cao đỉnh lớn nhất trong một trạng thái biển tĩnh
6.5.12 Chiều cao và chu kỳ điểm sóng
6.5.13 Sóng độc (Freak waves)
6.6 Thống kê sóng dài hạn
6.6.1 Các chiến lược phân tích
6.6.2 Phân phối biên của chiều cao sóng đáng kể
6.6.3 Phân phối chung của chiều cao và chu kỳ sóng đáng kể
6.6.4 Phân phối chung của chiều cao sóng đáng kể và tốc độ gió
6.6.5 Các hiệu ứng hướng (Directional effects)
6.6.6 Thống kê chung của gió biển và sóng lừng
6.6.7 Phân phối dài hạn của chiều cao sóng đơn
6.7 Phân phối giá trị cực đại
6.7.1 Trạng thái biển thiết kế
6.7.2 Đường biên môi trường
6.7.3 Chiều cao sóng đơn cực đại và chiều cao đỉnh cực đại
6.7.4 Chu kỳ sóng của chiều cao sóng đơn cực đại
6.7.5 Sự tiến triển của bão
7 Điều kiện dòng chảy và triều
7.1 Điều kiện dòng chảy
7.1.1 Quy định chung
7.1.2 Các loại dòng chảy
7.1.3 Vận tốc dòng chảy
7.1.4 Profile dòng chảy thiết kế
7.1.5 Sự mở rộng của dòng chảy đến mặt sóng
7.1.6 Mô phỏng số học của dòng chảy
7.1.7 Đo đạc dòng chảy
7.2 Điều kiện thủy triều
7.2.1 Độ sâu nước
7.2.2 Các mực thủy triều
7.2.3 Mực nước tĩnh trung bình
7.2.4 Mực nước dâng do bão
7.2.5 Mực nước tĩnh lớn nhất
8 Tải trọng gió
8.1 Quy định chung
8.2 Áp lực gió
8.2.1 Khái niệm áp lực gió
8.2.2 Hệ số áp lực gió
8.3 Lực gió
8.3.1 Lực gió - Quy định chung
8.3.2 Ảnh hưởng rắn (Solidification effect)
8.3.3 Hiệu ứng chắn
8.4 Hệ số hình dạng
8.4.1 Trụ tròn
8.4.2 Mặt cắt chữ nhật
8.4.3 Hiệu ứng chiều dài hữu hạn
8.4.4 Kết cấu hình cầu và parabol
8.4.5 Sàn đỡ trên mặt phẳng ngang
8.4.6 Hệ số ảnh hưởng hình dạng
8.5 Ảnh hưởng gió lên sàn sân bay
8.6 Phân tích động
8.6.1 Phân tích gió động
8.7 Mô hình thử
8.8 Tính toán động chất lỏng
9 Tải trọng do sóng và dòng chảy lên phần tử mảnh
9.1 Quy định chung
9.1.1 Lực cục bộ lên kết cấu mảnh
9.1.2 Công thức tải trọng Morrison
9.1.3 Định nghĩa thành phần lực
9.2 Lực pháp tuyến
9.2.1 Kết cấu cố định chịu tác động sóng và dòng chảy
9.2.2 Kết cấu di chuyển trong vùng nước tĩnh
9.2.3 Kết cấu di chuyển trong sóng và dòng chảy
9.2.4 Công thức vận tốc tương đối
9.2.5 Tính áp dụng của công thức vận tốc tương đối
9.2.6 Lực cản pháp tuyến lên trụ nghiêng
9.3 Lực tiếp tuyến lên trụ nghiêng
9.3.1 Quy định chung
9.4 Lực nâng
9.4.1 Quy định chung
9.5 Mô men xoắn
9.6 Hệ số thủy động học đối với dòng chảy đều
9.6.1 Thông số điều chỉnh
9.6.2 Hiệu ứng tác động tường chắn
9.7 Hệ số cản đối với trụ tròn
9.7.1 Ảnh hưởng của số Reynolds và độ nhám
9.7.2 Ảnh hưởng của số Keulegan-Carpenter
9.7.3 Hiệu ứng tác động tường chắn
9.7.4 Sự phát triển sinh vật biển
9.7.5 Độ khuếch đại cản do VIV
9.7.6 Hệ số cản lên tiết diện không tròn
9.8 Hệ số quy đổi do chiều dài hữu hạn
9.9 Hệ số quán tính
9.9.1 Ảnh hưởng của số KC và độ nhám
9.9.2 Hiệu ứng tác động tường chắn
9.9.3 Ảnh hưởng của mặt tự do
9.10 Hiệu ứng chắn và khuếch đại
9.10.1 Hiệu ứng rẽ nước
9.10.2 Hiệu ứng chắn từ nhiều trụ (shielding from multiple cylinders)
9.10.3 Ảnh hưởng của các kết cấu có thể tích lớn
9.11 Ống đứng với các phần tử nổi (Risers with bouyancy elements)
9.11.1 Quy định chung
9.11.2 Công thức tải trọng Morison đối với phần ống đứng có phần tử nổi
9.11.3 Khối lượng nước kèm của phần ống đứng với phần tử nổi
9.11.4 Lực cản lên mặt cắt ống đứng với các phần tử nổi
9.12 Thể tích đối tượng 3D nhỏ
9.12.1 Quy định chung
10 Tải trọng phát sinh do sóng và dòng chảy lên các kết cấu lớn
10.1 Quy định chung
10.2 Các chu kỳ dao động riêng
10.3 Tải trọng thủy tĩnh và quán tính
10.4 Tải trung bình và biến đổi chậm
11 Khoảng tĩnh không và va đập sóng
11.1 Quy định chung
11.2 Khoảng tĩnh không
11.2.1 Định nghĩa
11.3 Sóng vỗ sàn
11.3.1 Lực sóng vỗ sàn ngang
11.3.2 Lực sóng vỗ sàn theo phương đứng
11.3.3 Phương pháp rút gọn cho lực sóng vỗ sàn ngang
11.3.4 Phương pháp động lượng cho lực sóng vỗ sàn theo phương ngang
11.3.5 Phương pháp rút gọn cho lực tác động sóng theo phương đứng
11.3.6 Phương pháp động lượng cho lực sóng vỗ sàn thẳng đứng
11.3.7 Phản ứng nhiễu xạ từ kết cấu lớn
11.4 Tải tác động do sóng lên kết cấu mảnh
11.4.1 Phương pháp rút gọn
11.4.2 Va đập sóng trên kết cấu mảnh theo phương ngang
11.4.3 Va đập sóng lên kết cấu mảnh theo phương dọc
11.5 Tải trọng tác động do sóng lên các tấm
11.5.1 Tải va đập sóng trên một thân cứng
11.5.2 Lực va đập không gian trung bình
11.6 Tác động sóng vỡ
11.6.1 Áp lực sốc
11.7 Tổn thương mỏi do tác động sóng
11.7.1 Quy định chung
12 Dao động gây ra bởi dòng xoáy cảm ứng
12.1 Khái niệm và định nghĩa cơ bản
12.1.1 Khái niệm chung
12.1.2 Số Reynolds
12.1.3 Tần số xoáy
12.1.4 Lock-in
12.1.5 chuyển động ngang dòng và trong dòng
12.1.6 Vận tốc giảm
12.1.7 Tỷ lệ khối lượng
12.1.8 Tham số ổn định
12.1.9 Sức cản kết cấu
12.1.10 Sức cản thủy động lực
12.1.11 Khối lượng phản ứng
12.1.12 Biến khối lượng nước kèm
12.2 Sự tham gia của VIV
12.2.1 Quy định chung
12.2.2 Khuếch đại kéo do VIV
12.3 Xoáy do gió cảm ứng
12.3.1 Quy định chung
12.3.2 Rung dọc trục
12.3.3 Rung do dòng cắt ngang
12.3.4 Rung do xoáy gây ra của các phần tử trong kết cấu khung không gian
12.4 Dòng chảy gây ra dòng xoáy cảm ứng
12.4.1 Quy định chung
12.4.2 Nhiều trụ và bó ống
12.4.3 Mô hình phản ứng VIV dọc trục
12.4.4 Mô hình phản ứng VIV dòng vuông góc
12.5 Xoáy cảm ứng do sóng gây ra
12.5.1 Quy định chung
12.5.2 Sóng chuyển động thường xuyên và không thường xuyên
12.5.3 Dòng xoáy cảm ứng cho Keulegan-Carpenter số> 40
12.5.4 Dòng xoáy cảm ứng cho số Keulegan-Carpenter <40
13 Thử mô hình thủy động lực học
13.1 Giới thiệu
13.1.1 Quy định chung
13.1.2 Các loại và mục đích chung của mô hình thử
13.1.3 Tải trọng và phản ứng cực hạn
13.1.4 Phương pháp và quy trình thử
13.2 Khi nào được đề nghị mô hình thử
13.2.1 Quy định chung
13.2.2 Hệ thống khái niệm tổng thể và thẩm tra thiết kế
13.2.3 Thử thành phần kết cấu đơn lẻ
13.2.4 Hiệu lực của mô hình số phi tuyến
13.2.5 Tải và phản ứng cực hạn
13.3 Giới hạn và đơn giản hóa trong mô hình vật lý
13.4 Thiết lập hiệu chuẩn mô hình vật lý
13.4.1 Các mô hình có đáy cố định
13.5 Tỷ xích
13.5.1 Quy định chung
13.5.2 Vấn đề nhớt
13.5.3 Lựa chọn tỷ xích
13.5.4 Tỷ lệ chia đối với đo tải trọng va đập sóng
13.5.5 Các ảnh hưởng khác
Phụ lục A
Phụ lục B
Phụ lục C