CÔNG NGHỆ THÔNG TIN - KỸ THUẬT MẬT MÃ - THUẬT TOÁN MÃ DỮ LIỆU AES
Cryptographic technique - Cryptographic algorithms - Data Encryption Algorithm AES
Lời nói đầu
TCVN 7816 : 2007 được xây dựng trên cơ sở tham khảo tiêu chuẩn FIPS 197 và ISO /IEC18033-3.
TCVN 7816 : 2007 do Tiểu ban Kỹ thuật Tiêu chuẩn TCVN/JTC1/SC 27 "Các kỹ thuật mật mã" biên soạn, Ban cơ yếu Chính phủ đề nghị, Bộ Khoa học và Công nghệ công bố.
CÔNG NGHỆ THÔNG TIN - KỸ THUẬT MẬT MÃ - THUẬT TOÁN MÃ DỮ LIỆU AES
Information technology - Cryptographic technique - Data encryption algorithm AES
Tiêu chuẩn áp dụng cho việc mã hóa dữ liệu trong các hoạt động giao dịch điện tử của các tổ chức, công dân Việt Nam và tổ chức, công dân nước ngoài có quan hệ kinh tế - xã hội với tổ chức, công dân Việt Nam.
ISO/IEC 18033-3:2005, Information technology - Security techniques - Encryption algorithms - Part 3: Block ciphers (Công nghệ thông tin - Kỹ thuật mật mã - Các thuật toán mã hóa - Phần 3: Các khối mật mã).
FIPS PUB 197 - Announcing the Advance Encryption Standard (Thông báo về tiêu chuẩn mã hóa tiên tiến) (AES), NIST, 2001.
3.1. Thuật ngữ và các từ viết tắt
Tiêu chuẩn này sử dụng các khái niệm sau:
| AES | Tiêu chuẩn mã hóa tiên tiến. |
| Bản mã | Dữ liệu đầu ra của Phép mã hóa hoặc dữ liệu đầu vào của Phép giải mã. |
| Bản rõ | Dữ liệu đầu vào của Phép mã hóa hoặc dữ liệu đầu ra của Phép giải mã. |
| Bít | Một chữ số nhị phân có giá trị 0 hoặc 1. |
| Byte | Một nhóm gồm 8 bít được xem như là một thực thể đơn lẻ hoặc một thực mảng 8 bít đơn lẻ. |
| Hộp-S | Một bảng thay thế phi tuyến, được sử dụng trong một số phép thay thế byte và trong quy trình Mở rộng khóa, nhằm thực hiện một phép thay thế một-một đối với giá trị mỗi byte. |
| Khóa mã | Một số được giữ bí mật dùng cho quy trình Mở rộng khóa nhằm tạo ra một tập các Khóa vòng. |
| Khóa vòng | Các khóa vòng là các giá trị sinh ra từ Khóa mã bằng quy trình Mở rộng khóa, chúng được áp dụng lên Trạng thái trong Phép mã hóa và Phép giải mã. Trong thuật toán AES, Khóa vòng có thể xem như là một mảng chữ nhật của các byte có 4 hàng và Nk cột. |
| Khối | Dãy liên tiếp các bít nhị phân có thể là đầu vào, đầu ra, Trạng thái và Khóa vòng. Độ dài của một dãy là số lượng bít chứa trong dãy đó. Các khối cũng còn được xem như là một mảng các byte. |
| Mảng | Tập hợp ở dạng liệt kê các thực thể đồng nhất (ví dụ như mảng các byte). |
| Mở rộng khóa | Phép được sử dụng để tạo ra một loạt các khóa vòng từ một Khóa mã. |
| Phép biến đổi Affine | Phép biến đổi gồm phép nhân với một ma trận và phép cộng với một véc-tơ. |
| Phép giải mã | Một loạt các phép biến đổi để biến đổi bản mã thành bản rõ sử dụng một Khóa mã. |
| Phép mã hóa | Loạt các phép biến đổi để biến đổi bản rõ thành bản mã sử dụng Khóa mã. |
| Rijndael | Thuật toán mật mã được mô tả trong Tiêu chuẩn này. |
| Trạng thái | Kết quả mã hóa trung gian. Trong AES Trạng thái được mô tả dưới dạng một mảng chữ nhật của các byte có 4 hàng và Nb cột. |
| Từ | Một nhóm gồm 32 bít được xem như là một thực thể đơn lẻ hoặc như là một mảng 4 byte. |
3.2. Các tham số thuật toán, các ký hiệu và các hàm
Các tham số thuật toán, ký hiệu và hàm sau được sử dụng trong tiêu chuẩn này:
| AddRoundKey () | Phép biến đổi trong Phép mã hóa và Phép giải mã. Trong đó, một Khóa vòng được cộng thêm vào Trạng thái bằng phép toán XOR. Độ dài của Khóa vòng bằng độ dài của Trạng thái (chẳng hạn, nếu Nb = 4 thì độ dài của Khóa vòng là 128 bít hay 16 byte). |
| InvMixColumns () | Phép biến đổi dùng trong Phép giải mã, là phép nghịch đảo của MixColumns (). |
| InvShiftRows () | Phép biến đổi dùng trong Phép giải mã là phép nghịch đảo của ShiftRows () |
| InvSubBytes () | Phép biến đổi dùng trong Phép giải mã là phép nghịch đảo của SubBytes (). |
| K | Khóa mã. |
| MixColumns () | Phép biến đổi trong Phép mã hóa thực hiện bằng cách lấy tất cả các cột Trạng thái trộn với dữ liệu của chúng (một cách độc lập nhau) để tạo ra các cột mới. |
| Nb | Số các cột (các từ 32 bít) tạo nên Trạng thái. Trong tiêu chuẩn này, Nb = 4 (Xem thêm điều 6.3). |
| Nk | Số lượng các từ 32 bít trong Khóa mã. Trong tiêu chuẩn này, Nk = 4, 6 hoặc 8 (Xem thêm điều 6.3). |
| Nr | Số lượng vòng lặp, đó là một hàm của Nk và Nb (chúng là cố định). Trong tiêu chuẩn này, Nr = 10, 12 hoặc 14 (Xem thêm điều 6.3). |
| Rcon [ ] | Mảng từ hằng số vòng. |
| RotWord () | Hàm được sử dụng trong quy trình Mở rộng khóa bằng cách lấy một từ 4 byte và thực hiện một phép hoán vị vòng (quay vòng). |
| ShiftRows () | Phép biến đổi dùng trong Phép mã hóa áp dụng lên Trạng thái bằng cách chuyển dịch vòng ba hàng cuối của Trạng thái theo các offset khác nhau. |
| SubBytes () | Phép biến đổi dùng trong Phép mã hóa áp dụng lên Trạng thái sử dụng một bảng thay thế byte phi tuyến (Hộp-S) trên mỗi byte Trạng thái một cách độc lập. |
| SubWord () | Hàm được sử dụng trong phép Mở rộng khóa, lấy một từ đầu vào gồm 4 byte và áp dụng Hộp-S vào mỗi byte để tạo đầu ra là một từ. |
| XOR | Phép toán HOẶC-loại trừ. |
| Å | Phép toán HOẶC-loại trừ. |
| Ä | Phép nhân hai đa thức (có bậc < 4) theo modulo x4 + 1. |
| · | Phép nhân trên trường hữu hạn. |
4.1. Đầu vào và Đầu ra
Đầu vào và đầu ra của thuật toán AES là các dãy nhị phân 128 bít (chứa giá trị 0 hoặc 1). Các dãy bít này đôi khi được gọi là các khối và số lượng bít chứa trong dãy gọi là độ dài của dãy. Khóa mã dùng cho thuật toán AES là một dãy nhị phân 128, 192 hoặc 256 bít. Tiêu chuẩn này không cho phép sử dụng các đầu vào, đầu ra hoặc Khóa mã có độ dài khác với các kích thước trên.
Các bít trong các dãy nói trên sẽ được đánh số thứ tự từ không cho đến số cuối cùng. Số cuối cùng này là một số nhỏ hơn độ dài dãy (độ dài khối hay độ dài khóa) một đơn vị. Một số i ứng với một bít theo thứ tự sẽ có giá trị nằm trong khoảng 0 ≤ i < 128, 0 ≤ i < 192 hoặc 0 ≤ i < 256 phụ thuộc vào độ dài của khối và độ dài khóa (như đã đề cập ở phần trên).
4.2. Byte
Đơn vị xử lý cơ bản trong thuật toán AES, đó là một dãy 8 bít được xem như là một thực thể đơn lẻ. Các dãy đầu vào, đầu ra và Khóa mã đã nói ở điều 3.1 có thể biểu diễn theo các mảng byte bằng cách chia các dãy đó thành các nhóm 8 bít liên tiếp nhau (xem điều 3.3). Nếu đầu vào, đầu ra hoặc Khóa mã ký hiệu là a thì mảng byte thu được sẽ được tham chiếu đến theo một trong hai dạng: an hoặc a[n] trong đó n nằm trong khoảng giới hạn sau:
Nếu độ dài Khóa = 128 bít thì 0 ≤ n < 16; Độ dài Khối = 128 bít, 0 ≤ n < 16;
Nếu độ dài Khóa = 192 bít thì 0 ≤ n < 24;
Nếu độ dài Khóa = 256 bít thì 0 ≤ n < 32;
Tất cả giá trị byte trong thuật toán AES sẽ được biểu diễn dưới dạng ghép các bít riêng lẻ (0 hoặc 1) giữa các dấu ngoặc theo thứ tự {b7, b6, b5, b4, b3, b2, b1, b0,}. Các byte này được xem như là các phần tử trên trường hữu hạn bằng việc sử dụng biểu diễn đa thức:
![]()
Ví dụ, dãy bít {01100011} sẽ được biểu diễn thành phần tử trường hữu hạn là x6 + x4 + x + 1.
Cũng có thể biểu diễn các giá trị byte theo dạng thập lục phân (hexadecimal) bằng cách thay các nhóm 4 bít bằng một ký tự theo giá trị tương ứng cho bởi Hình 1.

Hình 1 - Ký hiệu thập lục phân tương ứng với các nhóm 4 bít
Chẳng hạn phần tử {01100011} được viết thành {63}, trong đó ký tự đại diện cho 4 bít cao sẽ được đặt bên trái.
Một số phép toán trên trường hữu hạn đòi hỏi thêm một bít (b8) vào bên trái của một byte 8-bít. Khi có mặt bít mở rộng theo cách này người ta đặt trước byte 8-bit ký hiệu ‘{01}’. Chẳng hạn, một dãy 9 bít sẽ được biểu diễn dưới dạng {01}{1b}.
4.3. Mảng byte
Các mảng byte được biểu diễn theo dạng sau:
a0a1a1 … a15
Cho một dãy 128 bít, nếu thứ tự các bít của dãy đầu vào này lần lượt là:
input0 input1 input2 ... input126 input127
thì mảng byte sẽ được xác định như sau:
a0 = {input0, input1, …, input7}
a1 = {input8, input9, ..., input15}
a15 = {input120, input121, …, input127}.
Cách này có thể áp dụng cho các dãy dài hơn (chẳng hạn cho dãy khóa 192 và 256 bít) một cách tổng quát như sau:
an = {input8n, input8n+1, …, input8n+7}. (3-2)
Đối chiếu điều 3.2 và điều 3.3, Hình 2 thể hiện cách các bít được đánh số thứ tự trong các byte:
| Dãy bít vào | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | … |
| Số hiệu byte | 0 | 1 | 2 | … | |||||||||||||||||||||
| TT bít trong byte | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | … |
Hình 2 - Cách thể hiện thứ tự các byte và bít
4.4. Trạng thái
Các phép toán của thuật toán AES được thực hiện trên một mảng byte hai chiều gọi là Trạng thái. Trạng thái bao gồm 4 hàng byte, mỗi hàng chứa Nb byte, trong đó Nb bằng số lượng từ trong một khối. Trong một mảng Trạng thái ký hiệu là s thì mỗi byte riêng biệt có hai chỉ số, chỉ số hàng ký hiệu là r, 0 ≤ r < 4, chỉ số cột ký hiệu là c, 0 ≤ c < Nb. Điều này cho phép mỗi byte riêng biệt của Trạng thái được tham chiếu đến theo dạng sr,c hoặc s[r,c]. Trong tiêu chuẩn này, Nb = 4, do đó 0 ≤ c < 4 (xem thêm điều 6.3).
Tại thời điểm bắt đầu Phép mã hóa hoặc Phép giải mã như sẽ mô tả trong điều 5 thì đầu vào là một mảng byte in0, in1, ... in15 sẽ được sao (copy) vào mảng Trạng thái như minh họa ở Hình 3. Các phép toán trên Phép mã hóa hoặc Phép giải mã tiếp theo được thao tác với mảng Trạng thái này, giá trị cuối cùng sẽ được copy đến đầu ra - đó là một mảng byte out0, out1, ... out15.

Hình 3 - Đầu vào và đầu ra mảng Trạng thái
Như vậy, vào thời điểm khởi đầu Phép mã hóa hoặc Phép giải mã, mảng đầu vào in được copy vào mảng Trạng thái theo lược đồ:
s[r,c] = in[r+4c] với 0 ≤ r < 4 và 0 ≤ c < Nb, (3.3)
và tại thời điểm kết thúc Phép mã hóa hoặc Phép giải mã, Trạng thái được copy vào mảng đầu ra out theo:
out[r + 4c] = s[r, c] với 0 ≤ r < 4 và 0 < c < Nb. (3.4)
4.5. Trạng thái được coi như một mảng các Cột
Bốn byte trên mỗi cột trong mảng Trạng thái tạo thành một từ 32 bít, trong đó số thứ tự của hàng r cho biết chỉ số của bốn byte trong mỗi từ. Vì thế có thể coi Trạng thái như là mảng một chiều chứa các từ 32 bít (các cột) w0...w3, trong đó số cột c cho biết chỉ mục trong mảng. Căn cứ vào Hình 3 thì Trạng thái có thể xem như là một mảng gồm bốn từ được xác định như sau:
w0 = s0,0 s1,0 s2,0 s3,0 w2 = s0,2 s1,2 s2,2 s3,2 (3.5)
w1 = s0,1 s1,1 s2,1 s3,1 w3 = s0,3 s1,3 s2,3 s3,3
5.1. Phép cộng
Phép cộng hai phần tử trên trường hữu hạn được thực hiện bằng cách “cộng" hệ số của các lũy thừa tương ứng trong các đa thức của hai phần tử. Phép cộng được thực hiện theo phép toán XOR (ký hiệu là Å). Tức là theo modulo 2 thì 1 Å 1 = 0, 1 Å 0 = 1 và 0 Å 0 = 0. Do đó, phép trừ đa thức cũng là phép cộng đa thức.
Việc cộng hai phần tử trên trường hữu hạn có thể được mô tả như phép cộng modulo 2 các bít tương ứng trong byte. Chẳng hạn, hai byte {a7a6a5a4a3a2a1a0} và {b7b6b5b4b3b2b1b0} sẽ có tổng là {c7c6c5c4c3c2c1c0}, trong đó mỗi bít ci = ai Å bi (tức là, c7 = a7Åb7, c6 = a6Åb6, ...c0 = a0Åb0).
Lấy ví dụ, các cách viết sau là tương đương nhau:
(x6 + x4 +x2 + x + 1) + (x7 + x + 1) = x7 + x6 + x4 + x2 (dạng đa thức)
{01010111} Å {10000011} = {11010100} (dạng nhị phân)
{57} Å {83} = {d4} (dạng thập lục phân)
5.2. Phép nhân
Trong cách biểu diễn đa thức, phép nhân trên trường GF(28) (ký hiệu là •) tương đương với phép nhân đa thức theo modulo của một đa thức bất khả qui bậc 8. Một đa thức được gọi là bất khả quy nếu nó chỉ có ước là 1 và chính nó. Đối với thuật toán AES, đa thức bất khả quy này là:
m(x) = x8 + x4 + x3 + x + 1 (4.1)
hoặc biểu diễn dưới dạng thập lục phân là {01}{1b}.
Ví dụ, {57} • {83} = {c1}, vì:
(x6 + x4 + x2 + x + 1)(x7 + x + 1) = x13 + x11 + x9 + x8 + x7 +
x7 + x5 + x3 + x2 + x +
x6 + x4 + x2 + x + 1
= x13 + x11 + x9 + x8 + x6 + x5 + x4 + x3 + 1
và
x13 + x11 + x9 + x8 + x6 + x5 + x4 + x3 +1 modulo (x8 + x4 + x3 + x + 1) = x7 + x6 + 1.
Phép rút gọn theo modulo m(x) cho ta kết quả là một đa thức nhị phân có bậc thấp hơn 8 vì thế có thể trình bày ở dạng byte. Không giống như phép cộng, không tồn tại phép toán đơn giản ở mức byte cho phép nhân.
Phép nhân định nghĩa ở trên có tính kết hợp và phần tử {01} gọi là phần tử đơn vị. Đối với bất cứ đa thức nhị phân khác không b(x) nào có bậc nhỏ hơn 8 thì phần tử nghịch đảo của b(x) ký hiệu là b-1(x), có thể tìm được như sau: Thuật toán Ơcơlit [7] mở rộng được sử dụng để tính ra đa thức a(x) và c(x) thỏa mãn:
b(x)a(x) + m(x)c(x) = 1 (4.2)
Bởi vì a(x) • b(x) mod m(x) = 1 cho nên
b-1(x) = a(x) mod m(x). (4.3)
Hơn nữa, với bất kỳ a(x), b(x) và c(x) trong trường, ta luôn có:
a(x) • (b(x) + c(x)) = a(x) • b(x) + a(x) • c(x).
Từ đó suy ra rằng, tập hợp 256 giá trị byte có thể với phép toán XOR và phép nhân được định nghĩa như trên sẽ có cấu trúc của trường hữu hạn GF(28).
5.2.1. Phép nhân với x
Nhân một đa thức nhị phân được định nghĩa trong điều (3.1) với đa thức x sẽ cho kết quả là đa thức:
b7x8 + b6x7 + b5x6 + b4x5 + b3x4 + b2x3 + b1x2 + b0x. (4.4)
Có thể tìm được kết quả của x • b(x) bằng cách rút gọn kết quả trên theo modulo m(x) như định nghĩa ở (4.1). Nếu b7 = 0 thì kết quả đã ở dạng rút gọn. Nếu b7 = 1 thì sự rút gọn đạt được bằng cách trừ đi (tức là phép XOR) với đa thức m(x). Từ đó suy ra, phép nhân với x (tức là x có giá trị {00000010} hoặc {02}) có thể được thực thi ở mức byte như là một phép dịch trái và một phép toán XOR có điều kiện ở mức bít với {1b}. Phép toán trên byte này ký hiệu là xtime(). Phép nhân với lũy thừa cao hơn của x có thể được thực hiện theo cách áp dụng lặp lại hàm xtime(). Bằng cách cộng các kết quả trung gian có thể thực hiện phép nhân với một byte bất kỳ.
Chẳng hạn, {57} • {13} = {fe} vì:
{57} • {02} = xtime({57}) = {ae}
{57} • {04} = xtime({ae}) = {47}
{57} • {08} = xtime({47}) = {8e}
{57} • {10} = xtime({8e}) = {07},
Do đó,
{57} • {13} = {57} • ({01} Å {02} Å {10})
= {57} Å {ae} Å {07}
= {fe}.
5.3. Đa thức với các hệ số trên trường GF(28)
Đa thức bốn hạng tử có thể được xác định với các hệ số là các phần tử trên trường hữu hạn có dạng:
a(x) = a3x3 + a2x2 + a1x + a0 (4.5)
Đa thức này sẽ được ký hiệu như một từ có dạng [a0, a1, a2, a3]. Chú ý rằng các đa thức trong phần này khác với các đa thức sử dụng khi định nghĩa về các phần tử trên trường hữu hạn, mặc dù cả hai dạng đa thức đều sử dụng cùng một biến x. Các hệ số của đa thức trong phần này bản thân đã là các phần tử trên trường hữu hạn, giá trị của chúng là các byte thay vì các bít. Ngoài ra, phép nhân các đa thức bốn hạng tử sử dụng một đa thức rút gọn khác sẽ được xác định dưới đây. Sự khác biệt này sẽ được làm sáng rõ trong trường hợp cụ thể.
Để minh họa cho các phép cộng và phép nhân đa thức, giả sử:
b(x) = b3x3 + b2x2 + b1x + b0 (4.6)
là một đa thức bốn hạng tử thứ hai. Phép cộng được thực hiện bằng cách cộng các hệ số trên trường hữu hạn tương ứng cùng bậc với x. Phép cộng này tương đương với một phép toán XOR giữa các byte tương ứng trong mỗi từ, nói cách khác là một phép XOR của các giá trị từ đầy đủ.
Từ (4.5) và (4.6), ta có:
a(x) + b(x) = (a3 Å b3)x3 + (a2 Å b2)x2 + (a1 Å b1)x + (a0 Å b0) (4.7)
Phép nhân được thực hiện qua hai bước. Bước thứ nhất, thực hiện khai triển đại số. Sau đó, gộp các số hạng cùng bậc. Kết quả cho ta tích:
c(x) = c6x6 + c5x5 + c4x4 + c3x3 + c2x2 + c1x + c0 (4.8)
Trong đó:
c0 = a0 • b0 c4 = a3 • b1 Å a2 • b2 Å a1 • b3
c1 = a1 • b0 Å a0 • b1 c5 = a3 • b2 Å a2 • b3
c2 = a2 • b0 Å a1 • b1 Å a0 • b2 c6 = a3 • b3 (4.9)
c3 = a3 • b0 Å a2 • b1 Å a1 • b2 Å a0 • b3
Kết quả thu được, c(x) không biểu diễn được bằng một từ 4 byte. Do đó, bước thứ hai là thực hiện phép nhân rút gọn c(x) theo modulo đa thức bậc 4. Kết quả có thể rút gọn thành một đa thức có bậc nhỏ hơn 4. Đối với thuật toán AES, đa thức này là x4 + 1, vì thế:
xi mod(x4 + 1) = ximod4 (4.10)
Phép nhân modulo giữa a(x) và b(x) ký hiệu là a(x) Ä b(x) cho kết quả là một đa thức bốn hạng tử d(x):
d(x) = d3x3 + d2x2 + d1x + d0 (4.11)
trong đó:
d0 = (a0 • b0) Å (a3 • b1) Å (a2 • b2) Å (a1 • b3)
d1 = (a1 • b0) Å (a0 • b1) Å (a3 • b2) Å (a2 • b3)
d2 = (a2 • b0) Å (a1 • b1) Å (a0 • b2) Å (a3 • b3) (4.12)
d3 = (a3 • b0) Å (a2 • b1) Å (a1 • b2) Å (a0 • b3)
Khi a(x) là một đa thức cố định thì phép toán chỉ ra trong biểu thức (4.11) có thể được viết dưới dạng ma trận như sau:
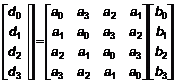 (4.13)
(4.13)
Do x4 +1 không phải là đa thức bất khả quy trên trường GF(28) nên phép nhân với một đa thức bất kỳ bốn hạng tử không nhất thiết phải có tính khả nghịch. Tuy nhiên, thuật toán AES sử dụng một đa thức cố định bốn hạng tử mà phép nhân với nó có tính khả nghịch (xem Phần 6.1.3 và Phần 6.3.3), đó là đa thức:
a(x) = {03}x3 + {01}x2 + {01}x + {02} (4.14)
a-1(x) = {0b}x3 + {0d}x2 + {09}x + {0e}. (4.15)
Một đa thức khác được sử dụng trong thuật toán AES (xem thêm về hàm RotWord () trong Phần 5.2) có a0 = a1 = a2 = {00} and a3 = {01} là đa thức x3. Xem kỹ biểu thức (4.13) ta thấy rằng hiệu quả của nó là ở chỗ nó biến đổi một từ đầu vào thành một từ đầu ra bằng phép quay vòng byte. Nghĩa là [b0, b1, b2, b3] được chuyển thành [b1, b2, b3, b0].
Đối với thuật toán AES, độ dài của khối đầu vào, khối đầu ra và Trạng thái đều là 128 bít. Như vậy Nb = 4 là số lượng các từ 32 bít (số cột) của Trạng thái.
Trong thuật toán AES, độ dài Khóa mã K có thể là 128, 192 hoặc 256 bít. Độ dài khóa được biểu diễn bằng một số Nk = 4, 6, hoặc 8 thể hiện số lượng các từ 32 bít (số cột) của Khóa mã.
Đối với thuật toán AES, số vòng được thay đổi trong quá trình thực thi thuật toán phụ thuộc vào kích cỡ khóa. Số vòng này được ký hiệu là Nr, trong AES, Nr = 10 khi Nk = 4, Nr = 12 khi Nk = 6 và Nr = 14 khi Nk = 8.
Các tổ hợp Khóa-Khối-Vòng phù hợp đối với tiêu chuẩn này cho bởi Hình 4. Việc thực thi cụ thể thuật toán có liên quan đến độ dài khóa, kích cỡ khối và số vòng nên xem thêm điều 6.3.
|
| Độ dài khóa (Nk từ) | Độ dài khối (Nb từ) | Số vòng |
| AES-128 | 4 | 4 | 10 |
| AES-192 | 6 | 4 | 12 |
| AES-256 | 8 | 4 | 14 |
Hình 4 - Các tổ hợp Khóa - Khối - Vòng
Đối với Phép mã hóa và Phép giải mã, thuật toán AES sử dụng một hàm vòng gồm bốn phép biến đổi byte: 1) phép thay thế byte sử dụng một bảng thay thế (Hộp-S), 2) phép dịch chuyển hàng của mảng Trạng thái theo các offset khác nhau, 3) phép trộn dữ liệu trong mỗi cột của mảng Trạng thái, 4) phép cộng Khóa vòng vào Trạng thái. Các phép biến đổi này (cũng như phép nghịch đảo của chúng) được mô tả trong điều 5.1.1 - 5.1.4 và 5.3.1 - 5.3.4.
Phép mã hóa và Phép giải mã được mô tả ở điều 5.1 và điều 5.3, Lược đồ khóa sẽ được mô tả ở điều 5.2.
6.1. Phép mã hóa
Tại thời điểm bắt đầu Phép mã hóa, đầu vào được sao vào mảng Trạng thái sử dụng các quy ước đã mô tả ở điều 3.4. Sau phép cộng Khóa vòng khởi đầu, mảng Trạng thái được biến đổi bằng cách thực thi một hàm vòng liên tiếp với số lần vòng lặp 10, 12 hoặc 14 (phụ thuộc vào độ dài khóa), vòng cuối cùng khác biệt không đáng kể với Nr - 1 vòng đầu tiên. Trạng thái cuối cùng được chuyển thành đầu ra như đã mô tả ở điều 3.4.
Hàm vòng được tham số hóa bằng cách sử dụng một lược đồ khóa là mảng một chiều chứa các từ bốn byte nhận từ phép Mở rộng khóa mô tả ở điều 5.2.
Phép mã hóa được mô tả theo dạng tựa mã ở Hình 5. Các phép biến đổi cụ thể - SubBytes (), Shif tRows (), MixColumns () và AddRoundKey () - dùng để xử lý Trạng thái được mô tả ở các mục tiếp theo. Ở Hình 5, mảng w [ ] có chứa một lược đồ khóa sẽ được mô tả ở điều 5.2.

Hình 5 - Đoạn tựa mã cho Phép mã hóa1
Như chúng ta đã thấy ở Hình 5, tất cả Nr vòng là giống hệt nhau chỉ có ngoại lệ ở vòng cuối cùng, vòng này không có phép biến đổi MixColumns ().
Phụ lục B trình bày một ví dụ về Phép mã hóa, chỉ ra cụ thể các giá trị của mảng Trạng thái tại thời điểm bắt đầu mỗi vòng và sau khi áp dụng bốn phép biến đổi.
6.1.1. Phép biến đổi SubBytes ()
Phép biến đổi SubBytes () là một phép thay thế phi tuyến được thực hiện độc lập trên mỗi byte của Trạng thái sử dụng một bảng thay thế (Hộp-S). Hộp-S này có tính khả nghịch được tạo bởi hai Phép biến đổi (Hình 7) sau:
1. Phép nghịch đảo trên trường hữu hạn GF(28), mô tả ở điều 4.2, trong đó phần tử {00} được ánh xạ vào chính nó.
2. Áp dụng phép biến đổi affine (trên trường GF(2)) sau:
b’j =bi Å b(i+4)mod 8 Å b(i+5)mod 8 Å b(i+6)mod8 Å b(i+7)mod 8 Å cj (6.1)
với 0 ≤ i < 8, trong đó bi là bít thứ i trong byte và ci là bít thứ i của một byte c có giá trị là {63} hoặc {01100011}. Từ đây về sau, dấu phẩy trên các biến (ví dụ b') có nghĩa là biến đã được cập nhật một giá trị nằm phía bên phải.
Ở dạng ma trận, phần tử của phép biến đổi affine trong Hộp-S có thể biểu diễn như sau:
 (6.2)
(6.2)
Hình 6 minh họa tác động của Phép biến đổi SubBytes () lên Trạng thái
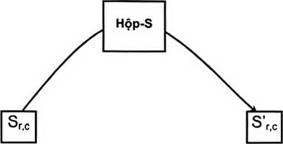
| Hình 6 | s0,0 | s0,1 | s0,2 | s0,3 |
| s'0,0 | s'0,1 | s'0,2 | s'0,3 | - Phép |
| s1,0 | s1,1 | s1,2 | s1,3 | s1,0 | s'1,1 | s'1,2 | s'1,3 | |||
| s2,0 | s2,1 | s2,2 | s2,3 | s'2,0 | s2,1 | s2,2 | s2,3 | |||
| s3,0 | s3,1 | s3,2 | s3,3 | s'3,0 | s'3,1 | s'3,2 | s'3,3 |
SubBytes () áp dụng Hộp-S vào mỗi byte của Trạng thái
Hộp-S sử dụng trong Phép biến đổi SubBytes () được trình bày ở dạng thập lục phân như trong Hình 7. Ví dụ, nếu s1,1 = {53}, thì giá trị thay thế được xác định bởi vị trí giao của hàng số “5" và cột số “3" trong Hình 7. Điều này cho kết quả s'1,1 là {ed
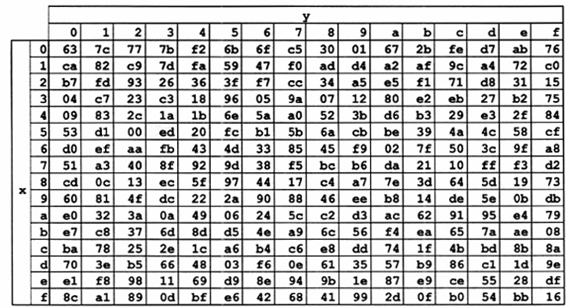
Hình 7 - Hộp-S: các giá trị thay thế cho byte {xy} (theo dạng thập lục phân)
6.1.2. Phép biến đổi ShiftRows ()
Trong phép biến đổi ShiftRows (), các byte ở ba hàng cuối của Trạng thái được dịch vòng theo số lượng byte khác nhau (các offset). Hàng đầu tiên, r = 0, không được dịch chuyển.
Cụ thể, Phép biến đổi ShiftRows () thực hiện như sau:
s’r,c = sr,(c + shift(r,Nb)) mod Nb với 0 < r < 4 và 0 ≤ c < Nb (6.3)
trong đó giá trị dịch chuyển shift(r,Nb) phụ thuộc vào số lượng hàng r, như sau (chú ý rằng Nb = 4):
shift(1,4) = 1; shift(2,4) = 2; shift(3,4) = 3 (5.4)
Hệ quả của việc này là di chuyển các byte từ vị trí thấp của hàng (là các giá trị thấp của c trong một hàng đã cho), trong khi các byte “thấp nhất” được đưa lên trên cùng của hàng (các giá trị cao của c trong một hàng đã cho).
Hình 8 minh họa Phép biến đổi ShiftRows ().
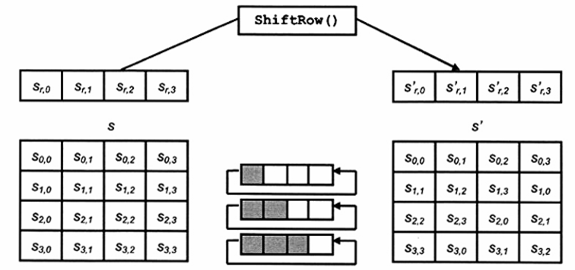
Hình 8 - Các phép dịch vòng trong ShiftRows () đối với ba hàng cuối của mã Trạng thái
6.1.3. Phép biến đổi MixColumns ()
Phép biến đổi MixColumns () trên Trạng thái được thực hiện theo từng cột, nghĩa là mỗi cột được xem như là một đa thức 4 hạng tử được mô tả ở điều 4.3. Các cột được coi là các đa thức trên trường GF(28) và được nhân theo modulo x4 + 1 với một đa thức cố định a(x) sau đây:
a(x) = {03}x3 + (01)x2 + {01}x + {02} (5.5)
Như đã mô tả ở điều 4.3, điều này có thể biểu diễn dưới dạng một phép nhân ma trận.
Giả sử s'(x) = a(x) Ä s(x):
 với 0 ≤ c < Nb (5.6)
với 0 ≤ c < Nb (5.6)
Ở kết quả của phép nhân này, bốn byte trong một cột được thay thế như sau:
s'0,c = ({02} • s0,c) Å ({03} • s1,c) Å s2,c Å s3,c
s'1,c = s0,c Å ({02} • s1,c) Å ({03} • s2,c) Å s3,c
s'2,c = s0,c Å s1,c Å ({02} • s2,c) Å ({03} • s3,c)
s'3,c = ({03} • s0,c) Å s1,c Å s2,c Å ({02} • s3,c)
Hình 9 minh họa Phép biến đổi MixColumns ().
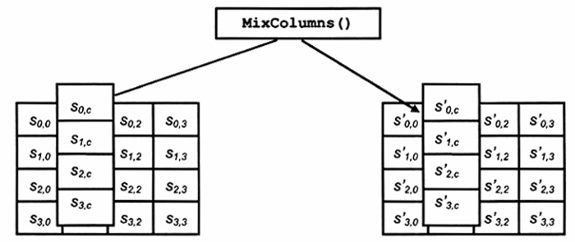
Hình 9 - Phép MixColumns () thao tác trên Trạng thái theo cách cột-cột
6.1.4. Phép biến đổi AddRoundKey ()
Trong Phép biến đổi AddRoundKey (), một Khóa vòng được cộng với Trạng thái bằng một phép toán XOR đơn giản trên bít. Mỗi Khóa vòng bao gồm Nb từ nhận được từ lược đồ khóa (mô tả ở điều 5.2). Nb từ này được cộng với các cột của Trạng thái sao cho:
[s'0,c, s'1,c, s'2,c, s'3,c] = [s0,c, s1,c, s2,c, s3,c] Å (wround*Nb+c] với 0 ≤ c < Nb (5.7)
Trong đó, [wi] là các từ của lược đồ khóa mô tả ở điều 5.2, round là một giá trị nằm trong 0 ≤ round ≤ Nr. Đối với Phép mã hóa, Phép cộng Khóa vòng ban đầu xảy ra khi round = 0, trước khi áp dụng lần đầu hàm vòng (xem Hình 5). Việc áp dụng Phép biến đổi AddRoundKey () theo Nr vòng của Phép mã hóa xảy ra khi 1 ≤ round ≤ Nr.
Các thao tác của Phép biến đổi này được minh họa ở Hình 10, trong đó I = round * Nb. Địa chỉ byte trong các từ của lược đồ khóa được mô tả ở điều 3.1.
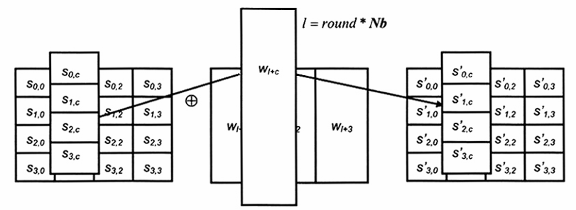
Hình 10 - Phép AddRoundKey () thực hiện XOR mỗi cột của Trạng thái với một từ của lược đồ khóa
6.2. Mở rộng khóa
Thuật toán AES nhận vào một Khóa mã K và thực hiện phép Mở rộng khóa để tạo ra một lược đồ khóa. Phép Mở rộng khóa tạo ra tổng số Nb (Nr + 1) từ: thuật toán yêu cầu một tập khởi tạo gồm Nb từ và mỗi trong số Nr vòng đòi hỏi Nb từ làm dữ liệu khóa đầu vào. Lược đồ khóa cuối cùng là một mảng tuyến tính các từ 4 byte ký hiệu là [wi], với i nằm trong khoảng 0 ≤ i < Nb(Nr + 1).
Quá trình mở rộng khóa đầu vào thành lược đồ khóa được biểu diễn ở dạng tựa mã như Hình 11.
SubWord () là một hàm nhận một từ 4 byte làm đầu vào và áp dụng Hộp-S (Phần 5.1.1 Hình 7) đối với mỗi byte để tạo thành đầu ra là một từ. Hàm RotWord () nhận một từ [a0,a1,a2,a3] làm đầu vào, thực hiện phép hoán vị tuần hoàn và cho kết quả đầu ra là một từ [a1,a2,a3,a0]. Mảng từ hằng số vòng Rcon[i] chứa các giá trị được cho bởi [xi-1,{00},{00},{00}], với xi-1 là lũy thừa của x (x được ký hiệu là {02}) trong trường GF(28) như đã mô tả ở điều 4.2 (chú ý i bắt đầu từ 1 chứ không phải từ 0).
Hình 11 cho thấy rằng Nk từ đầu tiên của khóa mở rộng được lấp đầy bởi Khóa mã. Mỗi từ tiếp sau đó (w[i]) đều tương đương với phép XOR của từ trước đó (w[i-1]) với từ trước đó Nk vị trí (w[i-Nk]). Đối với các từ ở các vị trí là bội số của Nk thì một phép biến đổi được áp dụng cho w[i-1] trước khi được XOR, tiếp đó một phép XOR với hằng của vòng Rcon [i] được áp dụng. Phép biến đổi này bao gồm một phép dịch vòng của các byte trong một từ (RotWord()), tiếp đến áp dụng một phép tra bảng cho cả bốn byte của từ (SubWord ()).
Một chú ý quan trọng là phép Mở rộng khóa cho các Khóa mã 256 bít (Nk = 8) có sự khác biệt không đáng kể so với phép Mở rộng khóa cho các Khóa mã 128 và 192 bít. Nếu Nk = 8 và i - 4 là bội số của Nk thì hàm Subword() được áp dụng cho w[i-1] trước khi áp dụng XOR.

Hình 11 - Tựa mã cho phép Mở rộng khóa2
Phụ lục A sẽ trình bày các ví dụ về phép Mở rộng khóa.
6.3. Phép giải mã
Các phép biến đổi trong Phép mã hóa ở điều 5.1 có thể được đảo ngược và sau đó thực thi theo chiều ngược lại nhằm tạo ra Phép giải mã trực tiếp của thuật toán AES. Các phép biến đổi sử dụng trong Phép giải mã là InvShiftRows (), InvSubBytes () , InvMixColumns () và AddRoundKey (), chúng sẽ thao tác với Trạng thái và được mô tả ở các mục tiếp sau đây.
Phép giải mã được mỏ tả ở dạng tựa mã như Hình 12. Trong hình này, mảng w [ ] chứa lược đồ khóa như đã mô tả ở điều 5.2 trước đây.

Hình 12 - Tựa mã về Phép giải mã3
6.3.1. Phép biến đổi InvShiftRows ()
Phép biến đổi lnvShiftRows () là phép biến đổi ngược của ShiftRows (). Các byte trong ba từ cuối của Trạng thái được dịch vòng theo số byte khác nhau (offset). Ở hàng đầu tiên (r = 0) không thực hiện phép chuyển dịch. Ba hàng dưới cùng được dịch vòng Nb - shift(r, Nb) byte, trong đó shift(r,Nb) phụ thuộc vào số dòng nhận được từ hệ thức (5.4) (xem điều 6.1.2).
Cụ thể, phép biến đổi lnvShiftRows () được thực hiện như sau:
sr, (c + shift(r.Nb)) mod Nb = s’r,c với 0 < r < 4 và 0 ≤ c < Nb (6.8)
Hình 13 minh họa phép biến đổi lnvShiftRows ().
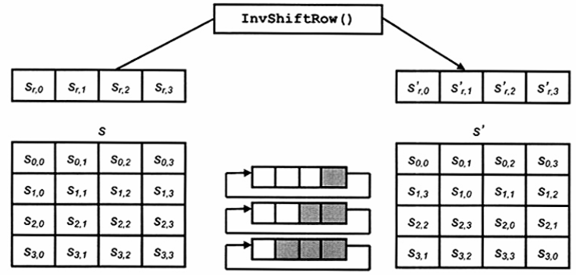
Hình 13 - Hàm InvShiftRows () chuyển dịch vòng ba hàng cuối của mã Trạng thái
6.3.2. Phép biến đổi InvSubBytes ()
Phép biến đổi InvSubBytes () là nghịch đảo của phép thay thế theo byte SubBytes (), trong đó sử dụng một Hộp-S nghịch áp dụng cho mỗi byte của Trạng thái. Điều này đạt được bằng cách áp dụng phép ngược của phép biến đổi affine (5.1) sau khi thực hiện phép nghịch đảo trên trường GF(28) cho bởi bảng dưới.
Hộp-S nghịch sử dụng trong phép biến đổi InvSubBytes () được trình bày ở Hình 14.
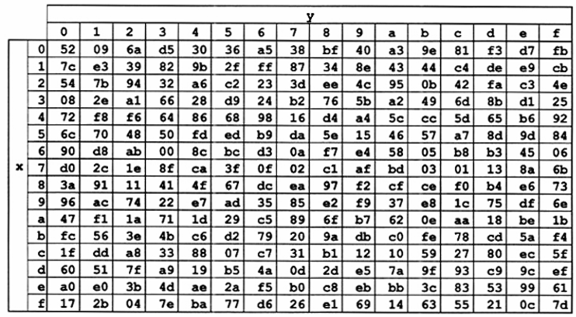
Hình 14 - Hộp-S nghịch: thay thế các giá trị theo byte {xy} (dạng thập lục phân)
6.3.3. Phép biến đổi InvMixColumns ()
Phép biến đổi InvMixColumns () là phép biến đổi ngược của MixColumns (). InvMixColumns () thao tác theo từng cột của Trạng thái, xem mỗi cột như một đa thức bốn hạng tử đã nói ở điều 4.3. Các cột được coi như các đa thức trên trường GF(28) và được nhân theo
modulo x4 + 1 với đa thức nghịch đảo của a(x) là a-1(x), tức là:
a-1(x) = {0b}x3 + {0d}x2 + {09}x + {0e} (5.9)
Như đã mô tả ở điều 4.3, nó có thể được biểu diễn như một phép nhân ma trận s'(x) = a-1(x) Å s(x) như sau:
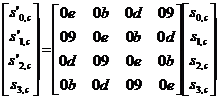 với 0 ≤ c < Nb (5.10)
với 0 ≤ c < Nb (5.10)
ở kết quả của phép nhân này, bốn byte trong một cột được thay thế bởi:
s'0,c = ({0e} • s0,c) Å ({0b} • s1,c) Å ({0d} • s2,c) Å ({09} • s3,c)
s'1,c = ({09} • s0,c) Å ({0e} • s1,c) Å ({0b} • s2,c) Å ({0d} • s3,c)
s'2,c = ({0d} • s0,c) Å ({09} • s1,c) Å ({0e} • s2,c) Å ({0b} • s3,c)
s'3,c = ({0b} • s0,c) Å ({0d} • s1,c) Å ({09} • s2,c) Å ({0e} • s3,c)
6.3.4. Phép biến đổi nghịch của AddRoundKey ()
Phép biến đổi AddRoundKey() đã được đề cập ở điều 5.1.4 là một phép biến đổi thuận nghịch vì nó chỉ áp dụng một phép toán XOR nên nó được thực hiện như nhau ở Phép mã hóa và Phép giải mã.
6.3.5. Phép giải mã tương đương
Trong Phép giải mã trình bày ở điều 5.3 và Hình 12, thứ tự của các phép biến đổi khác với thứ tự của các phép biến đổi của Phép mã hóa, trong khi đó khuôn dạng lược đồ khóa cho quá trình mã hóa và giải mã không thay đổi. Tuy nhiên, một số tính chất của thuật toán AES cho phép thực hiện một Phép giải mã tương đương có cùng thứ tự các phép biến đổi như trong Phép mã hóa (các biến đổi được thay bằng các phép biến đổi ngược). Có thể thực hiện điều này là nhờ một thay đổi trong lược đồ khóa.
Hai tính chất cấu thành một Phép giải mã tương đương là:
Tính giao hoán giữa hai phép biến đổi SubBytes () và ShiftRows (). Tính chất này nói lên rằng việc thực hiện phép biến đổi SubBytes () trước rồi thực hiện ShiftRows () cũng tương đương với việc thực hiện ShiftRows () trước rồi thực hiện SubBytes (). Điều này cũng đúng với phép nghịch đảo của chúng InvSubBytes () và InvShiftRows.
Các phép toán trộn cột MixColumns () và InvMixColumns () là tuyến tính đối với đầu vào cột, nghĩa là:
InvMixColumns(state XOR Round Key) =
InvMixColumns(state) XOR InvMixColumns(Round Key).
Các tính chất này cho phép đảo ngược thứ tự của các phép biến đổi InvSubBytes () và InvShiftRows (). Thứ tự của các phép biến đổi AddRoundKey () và InvMixColumns () cũng có thể đảo ngược với điều kiện đảm bảo rằng các cột (từ) của lược đồ khóa giải mã được sửa đổi bằng cách sử dụng phép biến đổi InvMixColumns ().
Phép giải mã tương đương được xác định bằng cách đảo thứ tự của phép biến đổi InvSubBytes () và lnvShiftRows () cho nhau như Hình 12 và đảo thứ tự của phép biến đổi AddRoundKey () và invMixColumns () được sử dụng trong “vòng lặp" for round = 1 to Nr-1 sau khi sửa đổi lần đầu lược đồ khóa mã sử dụng phép biến đổi InvMixColumns ().Theo phương pháp này, Nb từ đầu tiên và cuối cùng trong lược đồ khóa mã sẽ không bị sửa đổi.
Dựa trên các thay đổi này, Phép giải mã tương đương nhận được đưa ra một cấu trúc hiệu quả hơn Phép giải mã đã mô tả ở điều 5.3 và Hình 12. Tựa mã của Phép giải mã tương đương cho bởi Hình 15 (mảng từ dw [ ] chứa lược đồ khóa mã đã sửa đổi. Việc sửa đổi phép Mở rộng khóa cũng được cho bởi Hình 15).

Hình 15 - Tựa mã của Phép giải mã tương đương
7.1. Yêu cầu về độ dài khóa
Mỗi thực thi cụ thể của thuật toán AES sẽ hỗ trợ ít nhất một trong ba độ dài khóa chỉ ra trong điều 5: 128, 192 hoặc 256 bít (như vậy, Nk = 4, 6 hoặc 8). Các cài đặt có thể tùy chọn hỗ trợ hai hoặc ba độ dài khóa, chúng có thể tăng thêm tính tương tác cho các cài đặt thuật toán.
7.2. Các hạn chế về khóa
Chưa phát hiện ra khóa yếu hoặc khóa bán yếu đối với thuật toán AES và không có hạn chế nào đối với việc lựa chọn khóa.
7.3. Tham số hóa Độ dài khóa, Kích cỡ khối và Số vòng lặp
Tiêu chuẩn này định ra cụ thể các giá trị được phép dùng cho chiều dài khóa (Nk), kích cỡ khối (Nb) và số lượng vòng lặp (Nr) như Hình 4. Tuy nhiên, các xác nhận lại trong tương lai của tiêu chuẩn này có thể bao gồm những thay đổi hoặc bổ sung đối với các giá trị cho phép của tham số này. Bởi vậy, người cài đặt có thể lựa chọn để thiết kế cài đặt AES của họ tính đến sự mềm dẻo trong tương lai. Vì thế, trong quá trình thực thi thuật toán AES nên lựa chọn cách thiết kế có tính linh hoạt mong muốn.
7.4. Các đề xuất thực thi đối với các nền khác nhau
Trong nhiều trường hợp, rất có khả năng là sự khác nhau trong thực thi thuật toán ảnh hưởng đến hiệu năng hoặc các ưu điểm khác của thuật toán. Cho trước cùng một khóa và dữ liệu đầu vào (bản rõ hoặc bản mã), một cài đặt nào đó sinh ra cùng một đầu ra (bản mã hoặc rõ) như thuật toán đã mô tả trong chuẩn này đều được coi là một thực thi chấp nhận được của AES.
Các đề xuất về việc làm thế nào để thực thi hiệu quả thuật toán AES trên các nền khác nhau được trình bày trong tài liệu tham khảo [3] và một số bài báo trong tài liệu tham khảo [1].
7.5. Một số chỉ dẫn để thực thi thuật toán
7.5.1. Các chế độ hoạt động của AES
Khi cài đặt thuật toán mã AES người ta thường không sử dụng ở dạng nguyên gốc. AES thường hoạt động ở bốn chế độ cơ bản của mã khối n-bit (ECB, CBC, CFB và OFB) được quy định bởi tiêu chuẩn ISO/IEC 10116 : 1997, lnformation technology - Security techniques - Modes of operation for an n-bit cipher (Công nghệ thông tin - Kỹ thuật mật mã - Các thuật toán mã hóa - Phần 3: Các khối mật mã). Trên cơ sở bốn chế độ cơ bản ban đầu này người ta đã phát triển thêm một số chế độ khác (Có thể trong tương lai ISO/IEC sẽ công bố thêm một số chế độ hoạt động khác nữa cho mã khối. Tuy nhiên, hiện tại thì ISO/IEC vẫn mới quy định bốn chế độ cơ bản cho mã khối nói trên). Sau đây là những nét sơ lược của bốn chế độ này.
Chế độ sách mã điện tử ECB (Electronic Code Book): Trong chế độ ECB các khối rõ được mã hóa độc lập nhau và khối mã được giải mã độc lập: Ci = Ek(Mi); Mi = Dk(Ci), trong đó Ek và Dk là các phép mã hóa và giải mã theo khóa mật K.
Chế độ xích liên kết khối mã CBC (Cipher block Chaining): Trong chế độ này, đầu tiên người ta tạo ra một xâu nhị phân 64 bít được gọi là véc-tơ khởi đầu và thông báo cho nhau. Trong bước đầu tiên khối dữ liệu rõ M1 được cộng với véc-tơ khởi đầu theo phép cộng bít, kết quả nhận được sẽ được biến đổi qua các phép mã hóa để được đầu ra là khối mã C1. Ở các bước sau, mỗi khối Mi của bản rõ được cộng theo modulo 2 với bản mã trước đó Ci-1 và được mã hóa:
Ci = Ek(Mi Å Ci-1)
Mi = Dk(Ci) Å Ci-1
Chế độ mã liên kết ngược CFB (Cipher Feed Back): Chế độ này khác với chế độ CBC, tại bước đầu tiên véc-tơ khởi đầu được mã hóa bằng Ek rồi cộng theo modulo 2 với khối rõ. Kết quả thu được lại làm véc-tơ khởi đầu cho bước tiếp theo, rồi lại thực hiện tương tự chế độ CBC:
Ci = Mi Å Ek(Ci-1)
Mi = Ci Å Dk(Ci-1)
Chế độ đầu ra liên kết ngược OFB (Output Feedback): Thực chất của chế độ OFB là tạo ra khóa dòng rồi cộng theo modulo 2 với bản rõ. Khóa dòng được tạo như sau: Đầu tiên lấy véc-tơ khởi đầu s0 rồi mã hóa qua phép mã khối Ek được s1. Tiếp đó, s1 lại được mã hóa qua Ek để được s2,.. và cứ thế thực hiện cho đến khi tạo được khóa dòng có độ dài bằng dữ liệu cần mã.
Mỗi chế độ sử dụng mã khối trên đây đều có ưu điểm và nhược điểm riêng. Tùy từng trường hợp cụ thể mà người ta lựa chọn một chế độ sử dụng phù hợp đáp ứng yêu cầu bảo mật đặt ra.
7.5.2. Thực thi thuật toán AES bằng phần mềm
Thuật toán AES cho phép thực thi hiệu quả bằng cả phần mềm và phần cứng. Thông thường, với những ứng dụng không yêu cầu hiệu năng và tốc độ cao thì thuật toán thường được thực thi ở dạng phần mềm. Ngược lại, có những thiết bị phần cứng chuyên dụng cho phép thực thi thuật toán AES với tốt độ cao và khả năng vận hành bền vững.
Nếu xét về ngôn ngữ lập trình thì hiện có khá nhiều mã nguồn thực thi thuật toán AES được viết bằng nhiều ngôn ngữ lập trình (Assembler, C/C++, Visual Basic, Java, C#,...) có thể vận hành trên nhiều nền hệ điều hành (Windows, Linux/Unix, Solaris,...) chạy các vi xử lý dòng Intel, AMD,... Việc lựa chọn ngôn ngữ lập trình nào để thể hiện thuật toán AES tùy thuộc vào ý thích và khả năng của người lập trình cũng như mục đích, nền tảng phần cứng cho phép. Chẳng hạn, nếu với mục đích cứng hóa thuật toán thì người lập trình thường chọn các dạng ngôn ngữ ở thấp như hợp ngữ Assembler. Nếu hướng tới việc xây dựng các thư viện mật mã để thực thi trong nhân hệ điều hành hoặc sử dụng bởi ứng dụng khác thì người lập trình lại thường chọn ngôn ngữ C/C++. Nếu thực thi thuật toán trong các ứng dụng đồ họa thì người lập trình lại thường chọn các ngôn ngữ bậc cao như Visual Basic, Visual C++, Java, C#,.... Nếu viết để thực thi thuật toán AES trên nền web thì người lập trình thường chọn các ngôn ngữ hướng web như Java, VBScript, JavaScript, C#, ...Hiện nay, trên Internet có rất nhiều mã nguồn thực thi thuật toán AES do nhiều tác giả viết bằng nhiều dạng ngôn ngữ lập trình khác nhau. Tuy nhiên, chúng tôi khuyến cáo chỉ nên tham khảo một số mã nguồn thuật toán được cung cấp bởi các tác giả đáng tin cậy. Nên tham khảo web-site hỗ trợ nhiều thông tin về AES trên các web-site:
- http://csrc.nist.gov/archive/aes/.
- http://www.iaik.tu - graz.ac.at/research/krypto/aes/old/~rijment/rijndael/.
- http://fp.gladman.plus.conn/index.htm
- http://www.openssl.org
- http://tcmm.bcy.gov.vn
7.5.3. Thực thi thuật toán AES bằng phần cứng
Các thiết bị phần cứng thực thi thuật toán AES được chia làm hai dòng. Dòng thiết bị thứ nhất dựa vào một hệ vi xử lý kết phụ với hệ vi xử lý chính của máy tính (co-processor). Thông thường thiết bị thuộc dòng này được thiết kế ở dạng card chuyên dụng kết nối qua giao diện ghép nối với máy tính (ví dụ qua PCI). Dòng thiết bị thứ hai thường được thiết kế ở dạng thẻ thông minh (Smart Card) hoặc các thiết bị cắm qua cổng USB (USB Devices). Các thiết bị thuộc dòng thứ hai thường có một hệ vi xử lý (CPU) và bộ nhớ (ROM/RAM) riêng để thực thi thuật toán độc lập so với máy tính.
Công nghệ cứng hóa thuật toán hiện cũng tồn tại hai dòng. Dòng công nghệ thứ nhất sử dụng một kỹ thuật chuyên dụng chẳng hạn như ASIC (Application Specific Integrated Circuit). Công nghệ ASIC cho phép thực thi thuật toán rất nhanh và hiệu quả với năng lượng tiêu tốn rất ít. Tuy nhiên, công nghệ này có một số hạn chế như không cho phép sửa đổi thuật toán sau khi đã tạo thành thiết bị. Dòng công nghệ thứ hai sử dụng một bộ mạch tích hợp chứa hệ vi xử lý cho phép lập trình bằng phần mềm. Với công nghệ này, thuật toán có thể được cấu hình lại theo ý đồ của người lập trình nhưng vẫn cho phép thực thi thuật toán với tốc độ và hiệu quả cao. Điển hình cho dòng công nghệ này là các thiết bị sử dụng công nghệ FPGA (Field Programmable Gate Arrays). Hiện nay, công nghệ FPGA được coi là công nghệ có nhiều ưu điểm và được sử dụng trong hầu hết các thiết bị phần cứng thực thi thuật toán AES. Có thể tham khảo trang http://www.iaik.tu- graz.ac.at/research/krypto/AES/ để có thông tin đầy đủ hơn về các vấn đề thực thi thuật toán AES bằng phần cứng.
(tham khảo)
Phụ lục này trình bày việc thiết lập lược đồ khóa cho các kích cỡ khóa khác nhau. Chú ý là các giá trị chứa nhiều byte được trình bày theo cách viết mô tả ở điều 3. Các giá trị trung gian tạo ra trong quá trình phát triển lược đồ khóa (xem điều 5.2) cho bởi bảng sau (tất cả giá trị đều ở dạng thập lục phân, ngoại trừ cột số thứ tự (cột ký hiệu là i)).
A.1 Ví dụ về mở rộng một Khóa mã 128 bít
Cho một khóa mã dài 128 bít sau đây:
Cipher Key = 2b 7e 15 16 28 ae d2 a6 ab f7 15 88 09 cf 4f 3c
Với Nk = 4, các từ được xác định như sau:
w0 = 2b7e1516 w1 = 28aed2a6 w2 = abf71588 w3 = 09cf4f3c
Quá trình mở rộng Khóa được cho bởi bảng sau:
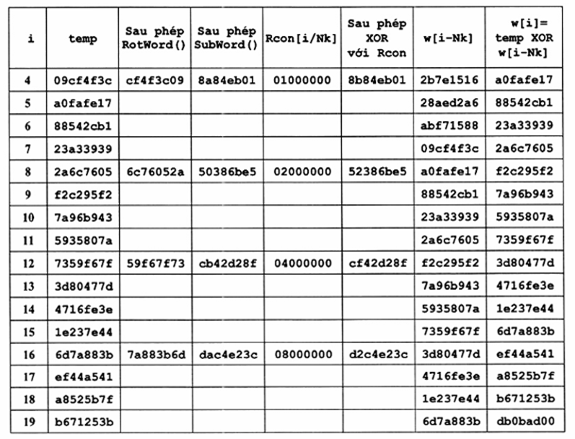
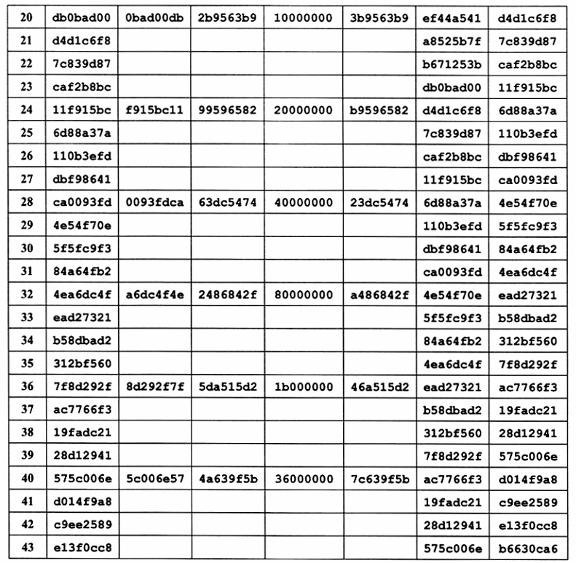
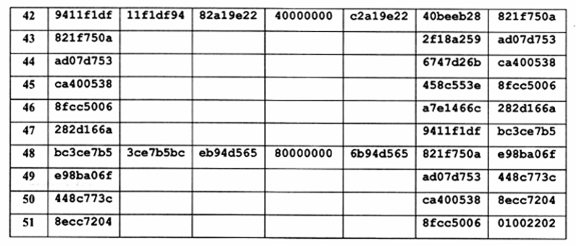
A.2 Ví dụ về mở rộng một Khóa mã 192 bít
Cho một khóa mã dài 192 bít sau đây:
Cipher Key = 8e 73 b0 f7 da 0e 64 52 c8 10 f3 2b
80 90 79 e5 62 f8 ea d2 52 2c 6b 7b
Với Nk = 6, các từ được xác định như sau:
w0 = 8e73b0f7 w1 = da0e6452 w2 = c810f32b w3 = 809079e5
w4 = 62f 8ead2 w5 = 522c6b7b
Quá trình mở rộng Khóa được cho bởi bảng sau:
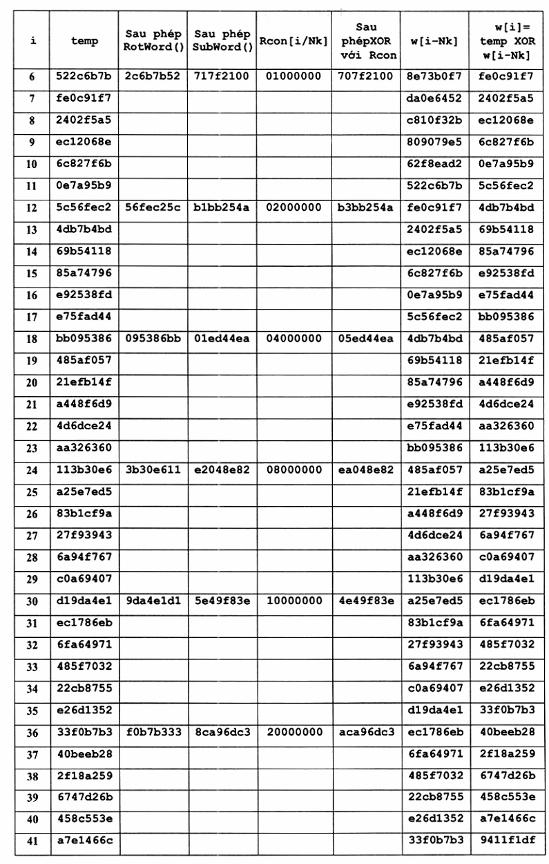
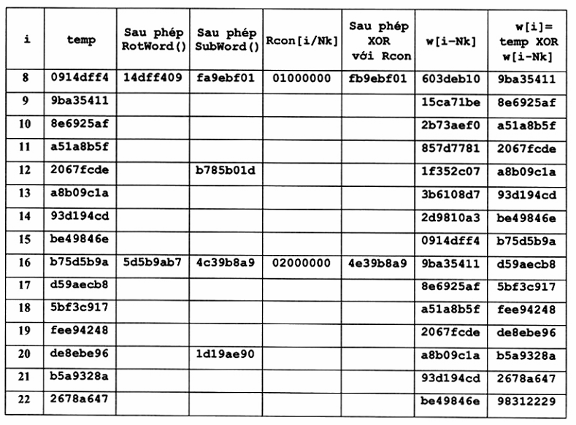
A.3 Ví dụ về mở rộng một Khóa mã 256 bít
Cho một khóa mã dài 256 bít sau đây:
Cipher Key = 60 3d eb 10 15 ca 71 be 2b 73 ae f0 85 7d 77 81
1f 35 2c 07 3b 61 08 d7 2d 98 10 a3 09 14 df f4
Với Nk = 8, các từ được xác định như sau:
w0= 603deb10 w1 = 15ca71be w2 = 2b73aef0 w3 = 857d7781
w4 = 1f352c07 w5 = 3b6108d7 w6 = 2d9810a3 w7 = 0914dff4
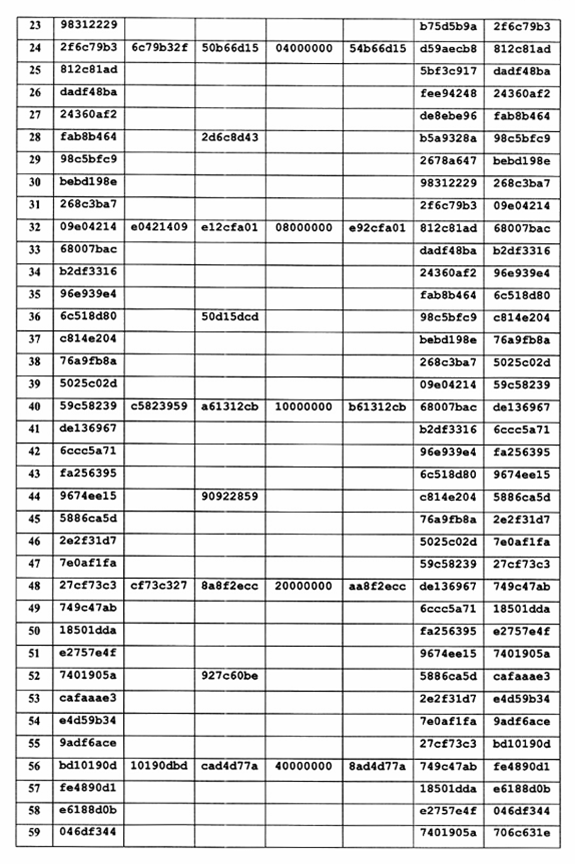
Quá trình mở rộng Khóa được cho bởi bảng sau:
(tham khảo)
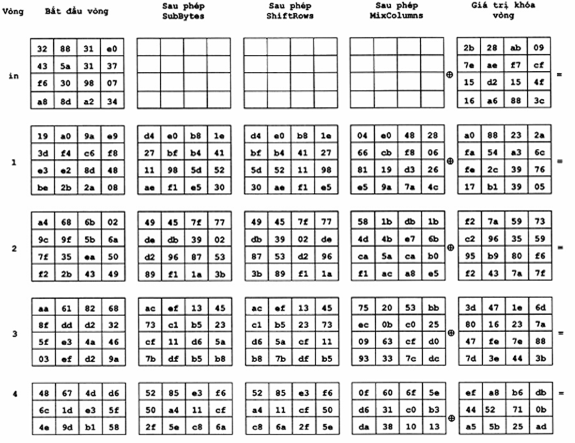
Sơ đồ sau trình bày các giá trị trong mảng Trạng thái của Phép mã hóa với độ dài khối và độ dài khóa mã là 16 byte (tức là Nb = 4 và Nk = 4).
Đầu vào:
Input = 32 43 f6 a8 88 5a 30 8d 31 31 98 a2 e0 37 07 34
Khóa mã:
Cipher Key = 2b 7e 15 16 28 ae d2 a6 ab f7 15 88 09 cf 4f 3c
Các giá trị của Khóa vòng nhận được từ phép Mở rộng khóa đã mô tả ở Phụ lục A. Toàn bộ quá trình mã hóa được mô tả chi tiết như sau:

(tham khảo)
Phụ lục này trình bày các véc-tơ ví dụ (chứa các giá trị trung gian) đối với cả ba trường hợp độ dài khóa (Nk = 4,6 và 8) cho Phép mã hóa, Phép giải mã và Phép giải mã tương đương như đã mô tả ở điều 5.1, 5.3 và 5.3.5. Có thể xem thêm các tài liệu tham khảo thêm [1] và [5].
Tất cả véc-tơ đều ở dạng thập lục phân, mỗi cặp ký tự mang giá trị của một byte trong đó ký tự bên trái là giá trị của 4 bít cao, còn ký tự bên phải mang giá trị của 4 bít thấp như đã đề cập ở d 3.2. Chỉ số mảng của tất cả các byte (gồm hai số thập lục phân) trong véc-tơ kiểm tra này bắt đầu từ giá trị không và tăng dần từ trái qua phải.
Ký hiệu dùng trong PHÉP MÃ HÓA (Số vòng r = 0 đến 10, 12 hoặc 14):
input: đầu vào Phép mã hóa
start: trạng thái bắt đầu của round[r]
s_box: trạng thái sau tác động của SubBytes ()
s_row: trạng thái sau tác động của ShiftRows ()
m_col: trạng thái sau tác động của MixColumns ()
k_sch: giá trị lược đồ khóa cho round[r]
output: đầu ra Phép mã hóa
Ký hiệu dùng trong PHÉP GIẢI MÃ (Số vòng r = 0 đến 10, 12 hoặc 14):
iinput: đầu vào của Phép giải mã
istart: trạng thái tại điểm bắt đầu của round[r]
is_box: trạng thái sau tác động của InvSubBytes ()
is_row: trạng thái sau tác động của InvShiftRows ()
ik_sch: giá trị lược đồ khóa cho round[r]
ik_add: trạng thái sau tác động của AddRoundKey ()
ioutput: đầu ra Phép giải mã
Ký hiệu dùng trong PHÉP GIẢI MÃ TƯƠNG ĐƯƠNG (GIẢI MÃ) (Số vòng r = 0 đến 10, 12 hoặc 14):
iinput: đầu vào Phép giải mã
istart: trạng thái tại điểm bắt đầu của round[r]
is_box: trạng thái sau tác động của InvSubBytes ()
is_row: trạng thái sau tác động của InvShiftRows ()
im_col: trạng thái sau tác động của InvMixColumns ()
ik_sch: giá trị lược đồ tạo khóa của round[r]
ioutput: đầu ra mã nghịch
round: biểu diễn thứ tự vòng
C.1 AES-128 (Nk=4, Nr=10)
![]()
MÃ THUẬN (MÃ HÓA):

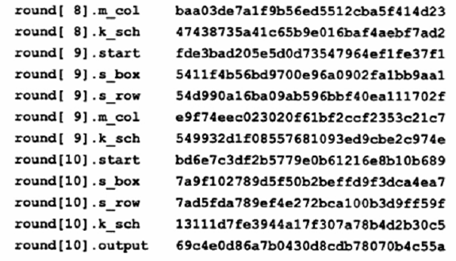
MÃ NGHỊCH (GIẢI MÃ):


GIẢI MÃ TƯƠNG ĐƯƠNG:


C.2 AES-192 (Nk=6, Nr=12)
![]()
MÃ THUẬN (MÃ HÓA):


MÃ NGHỊCH (GIẢI MÃ):

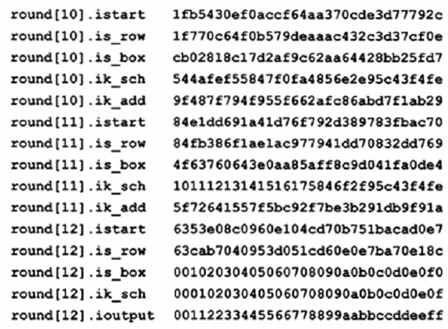
GIẢI MÃ TƯƠNG ĐƯƠNG:


C.3 AES-256 (Nk=8, Nr=14)
![]()
MÃ THUẬN (MÃ HÓA):



MÃ NGHỊCH (GIẢI MÃ):


GIẢI MÃ TƯƠNG ĐƯƠNG:



TÀI LIỆU THAM KHẢO
[1] Trang thông tin về AES của NIST http://www.nist.gov/CryptoToolkit.4
[2] Danh mục về các đối tượng an toàn máy tính (CSOR - Computer Security Objects Register) tại địa chỉ của NIST: http://csrc.nist.gov/csor/.
[3] J. Daemen và V. Rijmen, AES Proposal: Rijndael, AES Algorithm Submission (Đề xuất thuật toán AES, Bản đệ trình về thuật toán AES), 03/12/1999 có thể xem tại [1].
[4] J. Daemen and V. Rymen, The block cipher Rijdael, Smart Card research and Applications (Hệ mã khối Rijndael, Nghiên cứu và ứng dụng bằng Thẻ thông minh), LNCS 1820, Springer-Verlag, trang 288-296.
[5] Trang web liên quan đến AES của B. Gladman http://fp.gladman.plus.com/cryptography_technology/.
[6] A. Lee, NIST Special Publication 800-21, Guideline for Implementing Cryptography in the Federal Government, National Institute if Standard and Technology (Bản công bố đặc tả của NIST 800-21, Chỉ dẫn thực thi mật mã đối với cơ quan Chính phủ Liên bang, Viện Tiêu chuẩn và Công nghệ quốc gia Hoa Kỳ), 1999.
[7] A. Menezes, P. van Oorschot, và S. Vanstone, Handbook of Applied Cryptography (Sổ tay ứng dụng mật mã), CRC Press, New York, 1997, trang 81-83.
[8] J. Nechvatal, et. al., Report on the Development of the Advanced Encryption Standard (AES), National Institute if Standard and Technology (Báo cáo về việc Phát triển Chuẩn mã hóa tiên tiến (AES), Viện tiêu chuẩn và công nghệ quốc gia Hoa Kỳ), 02/10/2000, có tại [1].
MỤC LỤC
Lời nói đầu
1. Phạm vi áp dụng
2. Tài liệu viện dẫn
3. Thuật ngữ và định nghĩa
3.1. Thuật ngữ và các từ viết tắt
3.2. Các tham số thuật toán, các ký hiệu và các hàm
4. Các ký pháp và Quy ước
4.1. Đầu vào và Đầu ra
4.2. Byte
4.3. Mảng byte
4.4. Trạng thái
4.5. Trạng thái được coi như một mảng các Cột
5. Cơ sở toán học
5.1. Phép cộng
5.2. Phép nhân
5.3. Đa thức với các hệ số trên trường GF(28)
6. Quy định thuật toán
6.1. Phép mã hóa
6.2. Mở rộng khóa
6.3. Phép giải mã
7. Các vấn đề thực thi
7.1. Yêu cầu về độ dài khóa
7.2. Các hạn chế về khóa
7.3. Tham số hóa Độ dài khóa, Kích cỡ khối và Số vòng lặp
7.4. Các đề xuất thực thi đối với các nền khác nhau
7.5. Một số chỉ dẫn để thực thi thuật toán
Phụ lục A
A.1. Ví dụ về mở rộng một Khóa mã 128 bít
A.2. Ví dụ về mở rộng một Khóa mã 192 bít
Phụ lục B
Phụ lục C
C.1. AES-128 (Nk = 4, Nr = 10)
C.2. AES-192 (Nk = 6, Nr = 12)
C.3. AES-256 (Nk = 8, Nr = 14)
Tài liệu tham khảo
1 Một số phép biến đổi (vd: SubBytes(), ShiftRows(),...) thao tác trên mảng Trạng thái được tham chiếu bởi con trỏ "state". Phép biến đổi AddRoundKey() sử dụng một con trỏ khác để tham chiếu đến Khóa vòng.
2 Các hàm (SubWord() và RotWord()) trả về kết quả là một biến đổi của hàm đầu vào, trong khi các phép biến đổi trong Phép mã hóa và Phép giải mã (ShiftRow(), SubBytes()....) lại biến đổi mảng Trạng thái được tham chiếu bởi con trỏ "state".
3 Một số phép biến đổi (vd: lnvSubBytes(), lnvShiftRows()....) thao tác trên mảng Trạng thái được tham chiếu bởi con trỏ 'state'. Phép biến đổi AddRoundKey() sử dụng một con trỏ khác để tham chiếu đến Khóa vòng.
4 Một tập hoàn chỉnh tài liệu về các nỗ lực phát triển AES - bao gồm các thông báo, ý kiến công khai, bài báo phân tích, hội nghị,... có tại web - site này.

