CÁCH NHIỆT - CÁC ĐẠI LƯỢNG VẬT LÝ VÀ ĐỊNH NGHĨA
Thermal insulation - Physical quantities and definitions
Lời nói đầu
TCVN 9313 : 2012 hoàn toàn tương đương với ISO 7345 : 1987
TCVN 9313 : 2012 được chuyển đổi từ TCXDVN 299 : 2003 (ISO 7345 : 1987) theo quy định tại khoản 1 Điều 69 của Luật Tiêu chuẩn và Quy chuẩn kỹ thuật và điểm a), khoản 1, điều 7 Nghị định 127/2007/NĐ-CP quy định chi tiết thi hành một số điều của Luật tiêu chuẩn và Quy chuẩn kỹ thuật.
TCVN 9313 : 2012 do Viện Kiến trúc, Quy hoạch Đô thị và Nông thôn biên soạn, Bộ Xây dựng đề nghị, Tổng cục Tiêu chuẩn Đo lường Chất lượng thẩm định, Bộ Khoa học và Công nghệ công bố.
TCVN 9313:2012
CÁCH NHIỆT - CÁC ĐẠI LƯỢNG VẬT LÝ VÀ ĐỊNH NGHĨA
Thermal insulation - Physical quantities and definitions
Tiêu chuẩn này định nghĩa các đại lượng vật lý sử dụng trong lĩnh vực cách nhiệt và đưa ra các ký hiệu và đơn vị tương ứng.
CHÚ THÍCH: Do phạm vi của tiêu chuẩn này chỉ giới hạn trong lĩnh vực cách nhiệt nên một số định nghĩa đưa ra ở Điều 2 khác với những định nghĩa đưa ra trong TCVN 7870-5 : 2007. Để phân biệt sự khác nhau đó, trước các thuật ngữ có đánh dấu sao (*).
2. Các đại lượng vật lý và định nghĩa
Bảng 1 - Các đại lượng vật lý
| Tên gọi | Đại lượng | Đơn vị |
| 2.1. Nhiệt, nhiệt lượng | Q | J |
| 2.2. Lưu lượng dòng nhiệt: Nhiệt lượng truyền tới hoặc truyền từ một hệ thống chia cho thời gian: f = | F | W |
| 2.3. Cường độ dòng nhiệt: Lưu lượng dòng nhiệt chia cho diện tích: q = CHÚ THÍCH: Từ “cường độ” có thể thay thế bằng thuật ngữ “cường độ bề mặt” khi có thể nhầm lẫn với thuật ngữ “cường độ theo chiều dài” (Xem 2.4). | q | W/m2 |
| 2.4. Cường độ dòng nhiệt: Lưu lượng dòng nhiệt chia cho chiều dài: ql = | ql | W/m |
| 2.5. Hệ số dẫn nhiệt: Đại lượng được xác định theo biểu thức
CHÚ THÍCH: Khái niệm chính xác về hệ số dẫn nhiệt xem Phụ lục A. Khái niệm này cũng liên quan tới việc sử dụng khái niệm hệ số dẫn nhiệt cho vật liệu xốp đẳng hướng hoặc dị hướng, ảnh hưởng của nhiệt độ và các điều kiện thử nghiệm. | l | W/(m.K) |
| 2.6. Nhiệt trở suất: Đại lượng được xác định bởi biểu thức:
CHÚ THÍCH: Khái niệm chính xác về nhiệt trở suất xem Phụ lục A. | r | (m.K)/W |
| 2.7. * Nhiệt trở 1): Chênh lệch nhiệt độ chia cho cường độ dòng nhiệt trong trạng thái ổn định. R = CHÚ THÍCH: 1) Đối với một lớp phẳng khi sử dụng khái niệm hệ số dẫn nhiệt và khi tính chất không đổi hoặc tuyến tính với nhiệt độ (Xem Phụ lục A) thì: R = Trong đó: d là chiều dày của lớp phẳng. Các định nghĩa này giả thiết định nghĩa về hai nhiệt độ tham chiếu T1, T2 và một diện tích mà cường độ dòng nhiệt truyền qua đó là đồng nhất. Nhiệt trở có thể liên quan tới vật liệu, cấu trúc hoặc bề mặt. Nếu T1 hoặc T2 không phải là nhiệt độ của bề mặt chất rắn mà của bề mặt chất lỏng, thì nhiệt độ tham chiếu phải được xác định trong mỗi trường hợp cụ thể (có tham chiếu với sự truyền nhiệt đối lưu tự do hay cưỡng bức và bức xạ nhiệt từ các vật xung quanh...). Khi xác định giá trị nhiệt trở thì phải biết T1 và T2. 2) “Nhiệt trở” có thể thay thế bằng thuật ngữ “nhiệt trở bề mặt” khi nó có thể nhầm lẫn với thuật ngữ “nhiệt trở theo chiều dài” (Xem 2.8). | R | (m2.K)/W |
| 2.8. * Nhiệt trở theo chiều dài: Chênh lệch nhiệt độ chia cho cường độ dòng nhiệt theo chiều dài trong điều kiện ổn định: Rl = CHÚ THÍCH: Giả thiết về định nghĩa hai nhiệt độ T1, T2 và chiều dài mà cường độ theo chiều dài của dòng nhiệt là đồng nhất. Nếu bên trong hệ thống T1 hoặc T2 không phải là nhiệt độ của bề mặt chất rắn mà là của bề mặt chất lỏng thì nhiệt độ tham chiếu đó phải được xác định trong từng trường hợp cụ thể (có chú ý đến truyền nhiệt đối lưu hay cưỡng bức và bức xạ nhiệt từ các mặt xung quanh,...). Khi xác định giá trị nhiệt trở theo chiều dài thì phải biết T1 và T2. | Rl | (m.K)/W |
| 2.9. Hệ số trao đổi nhiệt bề mặt: Cường độ dòng nhiệt tại bề mặt trong điều kiện ổn định chia cho chênh lệch nhiệt độ giữa bề mặt đó và môi trường xung quanh. h = CHÚ THÍCH: Giả thiết về định nghĩa bề mặt truyền nhiệt, nhiệt độ bề mặt Ts, nhiệt độ không khí Ta là xác định (có sự tham chiếu với sự truyền nhiệt đối lưu tự do hay cưỡng bức và bức xạ từ các mặt xung quanh,...). | h | W/(m2.K) |
| 2.10. Độ dẫn nhiệt: Số nghịch đảo của nhiệt trở từ bề mặt này tới bề mặt kia trong điều kiện cường độ dòng điện là đồng nhất. A= CHÚ THÍCH: “Độ dẫn nhiệt” được thay thế bằng “độ dẫn nhiệt bề mặt” khi nó có thể bị nhầm lẫn với thuật ngữ “độ dẫn nhiệt theo chiều dài”. | A | W/(m2.K) |
| 2.11. Độ dẫn nhiệt theo chiều dài: Số nghịch đảo của nhiệt trở theo chiều dài từ bề mặt này tới bề mặt kia trong điều kiện cường độ dòng nhiệt là đồng nhất. L1 = | L1 | W/(m.K) |
| 2.12. Độ truyền nhiệt: Dòng nhiệt ở điều kiện ổn định chia cho tích số của diện tích và chênh lệch nhiệt độ của môi trường ở hai phía của hệ thống: U = CHÚ THÍCH: 1) Giả thiết định nghĩa về hệ thống, hai nhiệt độ tham chiếu T1, T2 và các điều kiện biên là xác định. 2) “Độ truyền nhiệt” được thay thế bằng thuật ngữ “Độ truyền nhiệt bề mặt” khi nó có thể nhầm lẫn với thuật ngữ “độ truyền nhiệt theo chiều dài” (Xem 2.13). 3) Số nghịch đảo của độ truyền nhiệt là tổng nhiệt trở của môi trường ở hai phía của hệ thống. | U | W/(m2.K) |
| 2.13. Độ truyền nhiệt theo chiều dài: Dòng nhiệt ở điều kiện ổn định chia cho tích số của chiều dài và chênh lệch nhiệt độ của môi trường ở hai phía của hệ thống: Ul = CHÚ THÍCH: 1) Giả thiết định nghĩa về hệ thống, hai nhiệt độ tham chiếu T1, T2 và các điều kiện biên là xác định. 2) Số nghịch đảo của độ truyền nhiệt theo chiều dài là tổng nhiệt trở theo chiều dài giữa môi trường ở hai phía của hệ thống. | Ul | W/(m.K) |
| 2.14. Nhiệt dung: Đại lượng được xác định bằng phương trình sau: C = CHÚ THÍCH: Khi nhiệt độ của hệ thống tăng lên một lượng dT do sự tăng thêm một lượng nhỏ nhiệt dQ thì đại lượng dQ/dT gọi là nhiệt dung. | C | J/K |
| 2.15. Nhiệt dung riêng: Nhiệt dung chia cho khối lượng | c | J/(kg.K) |
| 2.15.1. Nhiệt dung riêng ở áp suất không đổi | cp | J/(kg.K) |
| 2.15.2. Nhiệt dung riêng ở thể tích không đổi | cv | J/(kg.K) |
| 2.16. * Hệ số khuyếch tán nhiệt: Hệ số dẫn nhiệt chia cho tích số giữa khối lượng riêng và nhiệt dung riêng. a = CHÚ THÍCH: 1) Đối với chất lỏng, nhiệt dung riêng thích hợp là cp. 2) Định nghĩa này giả thiết môi trường đồng nhất, không trong suốt. 3) Hệ số dẫn nhiệt độ có liên quan tới trạng thái không ổn định và có thể đo trực tiếp hoặc tính toán bằng công thức trên từ các đại lượng được đo riêng rẽ. 4) Ngoài ra, hệ số dẫn nhiệt độ có kể đến sự thay đổi nhiệt độ ở bên trong khối vật liệu khi nhiệt độ ở bề mặt thay đổi. Hệ số dẫn nhiệt độ của vật liệu càng cao thì nhiệt độ bên trong vật liệu càng nhạy cảm với sự thay đổi của nhiệt độ bề mặt. | a | m2/s |
| 2.17. Hệ số hàm nhiệt: Căn bậc hai của tích số giữa độ dẫn nhiệt, khối lượng riêng và nhiệt dung riêng.
CHÚ THÍCH: 1) Đối với chất lỏng, nhiệt dung riêng thích hợp là cp. 2) Đặc tính này liên quan tới điều kiện không ổn định. Nó có thể được đo hoặc tính toán bằng công thức trên từ các đại lượng đo riêng rẽ. Ngoài ra, hệ số hàm nhiệt thể hiện sự thay đổi của nhiệt độ bề mặt vật liệu khi cường độ dòng nhiệt đi qua bề mặt thay đổi. Hệ số hàm nhiệt của vật liệu càng thấp thì nhiệt độ bề mặt càng nhạy cảm với sự thay đổi của dòng nhiệt tại bề mặt. | b | J/(m2.K.s1/2) |
3. Đặc tính năng lượng của công trình
Bảng 2 - Đặc tính năng lượng
| Tên gọi | Đại lượng | Đơn vị |
| 3.1. Hệ số tổn thất nhiệt theo thể tích: Dòng nhiệt từ công trình chia cho tích số thể tích và chênh lệch nhiệt độ giữa môi trường bên trong và bên ngoài: Fv = CHÚ THÍCH: Dòng nhiệt có thể bao gồm: các tác động truyền nhiệt qua vỏ bao che của công trình, hệ thống thông gió, bức xạ mặt trời,... Trong đó, đại lượng thể tích V phải được xác định. Khi áp dụng hệ số tổn thất nhiệt theo thể tích chấp nhận các định nghĩa về nhiệt độ bên trong, nhiệt độ bên ngoài, thể tích và các tác động nhiệt khác gây ra lưu lượng dòng nhiệt. | Fv | W/(m3.K) |
| 3.2. Hệ số tổn thất nhiệt theo diện tích: Dòng nhiệt từ công trình chia cho tích số diện tích và chênh lệch nhiệt độ giữa môi trường bên trong và bên ngoài: Fs = CHÚ THÍCH: Dòng nhiệt có thể bao gồm: các tác động truyền nhiệt qua vỏ bao che của công trình, hệ thống thông gió, bức xạ mặt trời,… Diện tích có thể là diện tích vỏ bao che, diện tích sàn,... Khi áp dụng hệ số tổn thất nhiệt theo thể tích chấp nhận các định nghĩa về nhiệt độ bên trong, nhiệt độ bên ngoài, thể tích và các tác động nhiệt khác gây ra lưu lượng dòng nhiệt. | Fs | W/(m2.K) |
| 3.3. Bội số trao đổi không khí: Số lần thay đổi không khí trong một thể tích xác định chia cho thời gian. CHÚ THÍCH: Đơn vị của bội số trao đổi không khí (h-1) không phải là đơn vị đo trong hệ SI. Tuy vậy, số lần thay đổi không khí trong một giờ nói chung được chấp nhận để thể hiện bội số trao đổi không khí. | n | h-1 |
4. Ký hiệu và đơn vị đo của các đại lượng khác
Bảng 3 - Ký hiệu và đơn vị đo các đại lượng khác
| Tên gọi | Đại lượng | Đơn vị |
| 4.1. Nhiệt độ động lực | T | K |
| 4.2. Nhiệt độ bách phân | q | °C |
| 4.3. Chiều dày | d | m |
| 4.4. Chiều dài | l | m |
| 4.5. Chiều rộng | b | m |
| 4.6. Diện tích | A | m2 |
| 4.7. Thể tích | V | m3 |
| 4.8. Đường kính | D | m |
| 4.9. Thời gian | t | S |
| 4.10. Khối lượng | m | Kg |
| 4.11. Khối lượng riêng | p | kg/m3 |
Để tránh nhầm lẫn, cần sử dụng những ký hiệu phụ hoặc các dấu hiệu nhận biết khác. Trong trường hợp đó ý nghĩa của chúng cần rõ ràng.
Những ký hiệu dưới đây được khuyến cáo sử dụng:
| - Bên trong (interior): | i |
| - Bên ngoài (exterior): | e |
| - Bề mặt (surface): | s |
| - Mặt trong (interior surface): | si |
| - Mặt ngoài (exterior surface): | se |
| - Dẫn nhiệt (conduction): | cd |
| - Đối lưu (convection): | cv |
| - Bức xạ (radiation): | r |
| - Tiếp xúc (contact): | c |
| - Không gian khí (không khí) (gas (air) space): | g |
| - Môi trường xung quanh (ambient): | a |
A.0. Giới thiệu
Để hiểu rõ thêm khái niệm độ dẫn nhiệt khi áp dụng, phụ lục này đưa ra cách giải thích theo toán học chính xác hơn.
A.1. Gradian nhiệt (grad T) tại điểm P
Đây là một véctơ theo hướng pháp tuyến n với mặt đẳng nhiệt chứa điểm P. Độ lớn của nó bằng đạo hàm của nhiệt độ T theo khoảng cách từ P dọc theo phương pháp tuyến n, véctơ đơn vị là ![]() .
.
Từ định nghĩa này có:
![]() (A.1)
(A.1)
A.2. Cường độ dòng nhiệt bề mặt q, ở điểm P (bề mặt có dòng nhiệt được truyền qua)
Được xác định như sau:
![]() (A.2)
(A.2)
Khi đề cập đến sự trao đổi nhiệt do dẫn nhiệt ở mỗi điểm của vật thể nơi tồn tại sự dẫn nhiệt thì đại lượng q phụ thuộc vào hướng của bề mặt (tức là phụ thuộc vào hướng pháp tuyến ở điểm P tới bề mặt diện tích A) và có thể tìm được hướng pháp tuyến n với bề mặt diện tích An chứa điểm P, nơi mà trị số q có giá trị lớn nhất và được ký hiệu bằng véctơ ![]() :
:
![]() (A.3)
(A.3)
Đối với bề mặt bất kỳ diện tích As đi qua điểm P, cường độ dòng nhiệt bề mặt q là một thành phần của véctơ ![]() theo hướng pháp tuyến tới bề mặt đó tại điểm P.
theo hướng pháp tuyến tới bề mặt đó tại điểm P.
Véctơ ![]() được gọi là “mật độ dòng nhiệt” (không phải cường độ dòng nhiệt). Bất kỳ khi nào véctơ
được gọi là “mật độ dòng nhiệt” (không phải cường độ dòng nhiệt). Bất kỳ khi nào véctơ ![]() không thể xác định được (đối với truyền nhiệt đối lưu và hầu hết các trường hợp truyền nhiệt bức xạ), thì chỉ sử dụng thuật ngữ “lưu lượng dòng nhiệt” và “cường độ dòng nhiệt bề mặt”.
không thể xác định được (đối với truyền nhiệt đối lưu và hầu hết các trường hợp truyền nhiệt bức xạ), thì chỉ sử dụng thuật ngữ “lưu lượng dòng nhiệt” và “cường độ dòng nhiệt bề mặt”.
A.3. Nhiệt trở suất r tại điểm P
Đây là đại lượng cho phép tính toán véctơ grad T tại điểm P từ véctơ ![]() tại điểm P bằng định luật Fourier. Trường hợp đơn giản nhất (vật liệu đẳng nhiệt) là khi grad T và
tại điểm P bằng định luật Fourier. Trường hợp đơn giản nhất (vật liệu đẳng nhiệt) là khi grad T và ![]() song song và ngược chiều, lúc đó r được xác định ở mỗi điểm như hệ số tỷ lệ giữa các véctơ grad T và
song song và ngược chiều, lúc đó r được xác định ở mỗi điểm như hệ số tỷ lệ giữa các véctơ grad T và ![]() .
.
![]() (A.4)
(A.4)
Trong trường hợp này r cũng là hệ số tỷ lệ nghịch giữa các thành phần của grad T và ![]() tại cùng một điểm dọc theo hướng s bất kỳ và không phụ thuộc vào hướng s đã chọn.
tại cùng một điểm dọc theo hướng s bất kỳ và không phụ thuộc vào hướng s đã chọn.
Trong trường hợp chung (vật liệu đẳng hướng hoặc dị hướng), một trong ba thành phần xác định grad T là đại lượng tỷ lệ tuyến tính của các thành phần của véctơ ![]() . Do đó nhiệt trở suất được xác định thông qua tenxơ [
. Do đó nhiệt trở suất được xác định thông qua tenxơ [![]() ] của chín hệ số của các đại lượng tỷ lệ tuyến tính đó theo hệ thức dưới đây:
] của chín hệ số của các đại lượng tỷ lệ tuyến tính đó theo hệ thức dưới đây:
![]() (A.5)
(A.5)
Nếu nhiệt trở suất r hoặc [![]() ] không đổi theo tọa độ và thời gian, có thể xem nó như là một đặc tính nhiệt ở nhiệt độ đã cho.
] không đổi theo tọa độ và thời gian, có thể xem nó như là một đặc tính nhiệt ở nhiệt độ đã cho.
A.4. Độ dẫn nhiệt l tại điểm P
Đây là đại lượng cho phép để tính toán véctơ ![]() tại điểm P từ véctơ grad T tại điểm P, có nghĩa là bằng tích số của độ dẫn nhiệt với nhiệt trở suất bằng một hoặc bằng một đơn vị tenxơ.
tại điểm P từ véctơ grad T tại điểm P, có nghĩa là bằng tích số của độ dẫn nhiệt với nhiệt trở suất bằng một hoặc bằng một đơn vị tenxơ.
Nếu ![]() và grad T song song và ngược chiều thì:
và grad T song song và ngược chiều thì:
![]()
lr = 1 (A.6)
Giống như nhiệt trở suất, độ dẫn nhiệt trong hầu hết các trường hợp là một tenxơ [![]() ] của chín hệ số của các đại lượng tỷ lệ tuyến tính thuộc các thành phần của grad T mà các hệ số này xác định mỗi thành phần của
] của chín hệ số của các đại lượng tỷ lệ tuyến tính thuộc các thành phần của grad T mà các hệ số này xác định mỗi thành phần của ![]() theo hệ thức dưới đây:
theo hệ thức dưới đây:
![]()
![]() (A.7)
(A.7)
Như vậy [![]() ] có thể được xác định được bằng cách đảo ngược [
] có thể được xác định được bằng cách đảo ngược [![]() ] và ngược lại. Nếu độ dẫn nhiệt l hoặc [
] và ngược lại. Nếu độ dẫn nhiệt l hoặc [![]() ] không đổi theo tọa độ và thời gian, nó có thể được xem như là một đặc tính nhiệt ở nhiệt độ đã cho.
] không đổi theo tọa độ và thời gian, nó có thể được xem như là một đặc tính nhiệt ở nhiệt độ đã cho.
Độ dẫn nhiệt có thể là một hàm số của nhiệt độ và của hướng (vật liệu dị hướng). Do đó cần biết mối quan hệ của các thông số này.
Hãy xem xét một vật thể có chiều dày d được giới hạn bằng hai mặt phẳng song song và đẳng nhiệt, có nhiệt độ T1 và T2, mỗi mặt có diện tích A.
Các mép bên bao quanh các mặt chính của vật thể này được giả thiết là đoạn nhiệt và thẳng góc với chúng. Giả thiết rằng vật thể được tạo bởi vật liệu ổn định, đồng nhất và đẳng hướng (hoặc không đẳng hướng - dị hướng - với một trục đối xứng vuông góc với các mặt chính). Trong điều kiện như vậy các hệ thức dưới đây = đạo hàm từ định luật Fourier trong các trạng thái ổn định sẽ được áp dụng nếu hệ số dẫn nhiệt l hoặc [![]() ], hoặc nhiệt trở suất r hoặc [
], hoặc nhiệt trở suất r hoặc [![]() ] không phụ thuộc nhiệt độ:
] không phụ thuộc nhiệt độ:
![]() (A.8)
(A.8)
Nếu tất cả các điều kiện trên được đáp ứng (ngoại trừ hệ số dẫn nhiệt l hoặc [![]() ] là hàm số tuyến tính của nhiệt độ) thì vẫn áp dụng các hệ thức trên nhưng hệ số dẫn nhiệt được tính ở nhiệt độ trung bình.
] là hàm số tuyến tính của nhiệt độ) thì vẫn áp dụng các hệ thức trên nhưng hệ số dẫn nhiệt được tính ở nhiệt độ trung bình.
![]()
Tương tự, nếu một vật thể có chiều dài l được giới hạn bởi hai mặt đẳng nhiệt, hình lăng trụ, đồng trục có nhiệt độ T1 và T2 và đường kính Di và De tương ứng, và nếu hai đầu của vật thể là các mặt đoạn nhiệt phẳng vuông góc với hình lăng trụ, và các vật liệu là ổn định, đồng nhất và đẳng hướng, thì các hệ thức dưới đây bằng đạo hàm từ định luật Fourier trong các điều kiện ổn định sẽ được áp dụng nếu độ dẫn nhiệt l hoặc nhiệt trở suất r không phụ thuộc vào nhiệt độ:
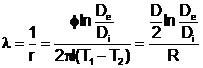 (A.10)
(A.10)
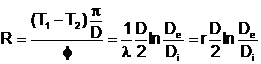 (A.11)
(A.11)
Trong đó D có thể là đường kính bên ngoài hoặc bên trong hoặc đường kính xác định khác.
Nếu tất cả các điều kiện trên đều được đáp ứng ngoại trừ hệ số dẫn nhiệt l một hàm số tuyến tính của nhiệt độ thì các hệ thức trên vẫn được áp dụng nhưng hệ số dẫn nhiệt được tính theo nhiệt độ trung bình qua biểu thức sau:
Với những giới hạn trên, công thức (8) và (10) thường được sử dụng để xác định hệ số dẫn nhiệt của môi trường không trong suốt, đồng nhất từ các đại lượng đã đo được ở nhiệt độ trung bình Tm.
Tương tự, công thức (A.8) và (A.10) còn thường được dùng để xác định đặc tính nhiệt của các môi trường xốp từ các đại lượng đo được mà đối với chúng quá trình truyền nhiệt tổng hợp bao gồm ba phương thức: bức xạ, dẫn nhiệt và đôi khi cả đối lưu nhiệt.
Đặc tính nhiệt đo được đại diện cho tất cả các phương thức truyền nhiệt nêu trên được gọi là độ dẫn nhiệt (đôi khi còn gọi là độ dẫn nhiệt biểu kiến, tương đương hoặc hiệu quả) của môi trường xốp đồng nhất khi nó không phụ thuộc vào kích thước hình học của mẫu đo, tính chất bức xạ nhiệt của các bề mặt giới hạn của mẫu đo và chênh lệch nhiệt độ (T1 - T2).
Khi các điều kiện đó không thỏa mãn, nhiệt trở bề mặt phải được sử dụng để biểu thị đặc tính của mẫu đo với các kích thước hình học, chênh lệch nhiệt độ (T1 - T2) và với độ bức xạ nhiệt đã cho của các mặt bên của mẫu đo.
THƯ MỤC TÀI LIỆU THAM KHẢO
[1] TCVN 7870-5 : 2007, Đại lượng và đơn vị - Phần 5: Nhiệt động lực học.
MỤC LỤC
1. Phạm vi áp dụng
2. Các đại lượng vật lý và định nghĩa
3. Đặc tính năng lượng của công trình
4. Ký hiệu và đơn vị đo của các đại lượng khác
5. Các ký hiệu phụ
Phụ lục A

