LẤY MẪU NGẪU NHIÊN VÀ QUY TRÌNH NGẪU NHIÊN HÓA
Random sampling and randomization procedures
Lời nói đầu
TCVN 9600:2013 hoàn toàn tương đương với ISO 24153:2009;
TCVN 9600:2013 do Ban Kỹ thuật tiêu chuẩn quốc gia TCVN/TC 69 Ứng dụng các phương pháp thống kê biên soạn,Tổng Cục Tiêu chuẩn và Đo lường Chất lượng đề nghị, Bộ Khoa học và Công nghệ công bố.
Lời giới thiệu
Lấy mẫu ngẫu nhiên và quy trình ngẫu nhiên là cơ sở để xác nhận giá trị của nhiều phương pháp thống kê sử dụng trong thử nghiệm, dù là cho mục đích kiểm soát chất lượng công nghiệp và cải tiến hay cho thiết kế thực nghiệm trong lĩnh vực y tế, sinh học, nông nghiệp hay lĩnh vực cụ thể khác. Nhiều tiêu chuẩn thống kê đề cập đến việc tiến hành thử nghiệm như vậy. Đặc biệt, tất cả các tiêu chuẩn lấy mẫu chấp nhận dưới đây đều được thiết kế trên tiền đề là lấy mẫu ngẫu nhiên được sử dụng để lựa chọn đơn vị lấy mẫu cần thiết ứng với bố trí lô:
TCVN 7790 (ISO 2859) (tất cả các phần), Qui trình lấy mẫu để kiểm tra định tính
TCVN 8243 (ISO 3951) (tất cả các phần), Qui trình lấy mẫu để kiểm tra định lượng
TCVN 9601 (ISO 8422), Phương án lấy mẫu liên tiếp để kiểm tra định tính
ISO 8423, Phương án lấy mẫu liên tiếp để kiểm tra định lượng phần trăm không phù hợp (đã biết độ lệch chuẩn)
ISO 13448 (tất cả các phần), Qui trình lấy mẫu chấp nhận dựa trên phân bổ nguyên tắc ưu tiên (APP)
ISO 14560, Qui trình lấy mẫu chấp nhận định tính – Mức chất lượng quy định về số cá thể không phù hợp trên một triệu
ISO 18414, Qui trình lấy mẫu chấp nhận định tính – Hệ thống lấy mẫu chấp nhận không dựa trên nguyên tắc tin cậy đối với kiểm soát chất lượng đầu ra
ISO 21247, Hệ thống lấy mẫu chấp nhận không kết hợp và qui trình kiểm soát quá trình để chấp nhận sản phẩm
Ngoài ra, TCVN 7790-3 (ISO 2859-3) và ISO 21247 bao gồm các quy định đối với lấy mẫu ngẫu nhiên được áp dụng để xác định xem lô có cần kiểm tra hoặc không áp dụng qui trình lấy mẫu lô cách quãng hay không, đồng thời để quyết định đơn vị nào cần kiểm tra từ một quá trình sản xuất trong phương án lấy mẫu liên tục, một cách tương ứng. Do đó, điều quan trọng là hiệu lực của tất cả các tiêu chuẩn trên để áp dụng lấy mẫu ngẫu nhiên hiệu quả.
Mặc dù các nguyên tắc của tiêu chuẩn này có thể áp dụng chung trong trường hợp yêu cầu lấy mẫu ngẫu nhiên và có thể xác định rõ đơn vị lấy mẫu, ưu tiên trên cơ sở cá thể riêng rẽ, nhưng có nhiều tình huống trong đó vật liệu quan tâm không được xác định là cá thể riêng rẽ, như trong trường hợp vật liệu dạng đống. Trong tình huống này, người sử dụng cần tham khảo tiêu chuẩn ISO sau đây để có hướng dẫn thích hợp:
ISO 11648 (tất cả các phần), Khía cạnh thống kê của mẫu lấy từ vật liệu dạng đống.
LẤY MẪU NGẪU NHIÊN VÀ QUY TRÌNH NGẪU NHIÊN HÓA
Random sampling and randomization procedures
Tiêu chuẩn này quy định các quy trình lấy mẫu ngẫu nhiên và ngẫu nhiên hóa. Nhiều phương pháp được đưa ra, bao gồm cả các phương pháp dựa trên thiết bị cơ khí, bảng số ngẫu nhiên và thuật toán trên máy tính xách tay.
Tiêu chuẩn này áp dụng trong trường hợp quy định, hợp đồng hay tiêu chuẩn khác yêu cầu sử dụng lấy mẫu ngẫu nhiên hay ngẫu nhiên hóa. Các phương pháp áp dụng cho các trường hợp như
a) lấy mẫu chấp nhận các đơn vị riêng rẽ để kiểm tra theo lô,
b) lấy mẫu cho mục đích khảo sát,
c) đánh giá kết quả của hệ thống quản lý chất lượng, và
d) chọn đơn vị thử nghiệm, phân bổ cách xử lý chúng và xác định thứ tự đánh giá trong tiến hành các thiết kế thực nghiệm.
Ngoài ra, tiêu chuẩn còn có các thông tin để hỗ trợ việc đánh giá hay xem xét bên ngoài khác các kết quả lấy mẫu ngẫu nhiên hay ngẫu nhiên hóa theo yêu cầu của nhân sự quản lý chất lượng hay cơ quan chế định.
Tiêu chuẩn này không cung cấp hướng dẫn như quy trình lấy mẫu ngẫu nhiên hay ngẫu nhiên hóa thích hợp để sử dụng cho tình huống thực nghiệm cụ thể bất kỳ hoặc đưa ra hướng dẫn về việc lựa chọn chiến lược lấy mẫu hay xác định cỡ mẫu. Cần tham khảo các tiêu chuẩn khác (như liệt kê trong phần Lời giới thiệu) hoặc các tài liệu viện dẫn hợp lệ hướng dẫn về vấn đề này.
Tài liệu viện dẫn dưới đây rất cần thiết cho việc áp dụng tiêu chuẩn này. Đối với các tài liệu ghi năm công bố thì áp dụng bản được nêu. Đối với các tài liệu không ghi năm công bố thì áp dụng bản mới nhất, bao gồm cả các sửa đổi.
TCVN 7870-2 (ISO 80000-2), Đại lượng và đơn vị - Phần 2: Dấu và ký hiệu toán học sử dụng trong khoa học tự nhiên và công nghệ
TCVN 8244-1 (ISO 3534-1), Thống kê học – Từ vựng và ký hiệu – Phần 1: Thuật ngữ chung và thống kê thuật ngữ dùng trong xác suất
TCVN 8244-2 (ISO 3534-2), Thống kê học – Từ vựng và ký hiệu – Phần 2: Thống kê ứng dụng
ISO 3534-3, Statistics – Vocabulary and symbols – Part 3: Design of experiments (Thống kê học – Từ vựng và ký hiệu – Phần 3: Thiết kế thực nghiệm)
3. Thuật ngữ, định nghĩa và ký hiệu
Tiêu chuẩn này áp dụng các thuật ngữ và định nghĩa trong TCVN 8244-1 (ISO 3534-1), TCVN 8244-2 (ISO 3534-2), ISO 3534-3 và các thuật ngữ, định nghĩa dưới đây.
3.1. Thuật ngữ và định nghĩa
3.1.1. Chùm (cluster)
Bộ phận của tổng thể (3.1.6) chia tách thành các nhóm đơn vị mẫu (3.1.13) tách biệt nhau theo một cách thức nhất định.
[TCVN 8244-2:2010 (ISO 3534-2:2006), 1.2.28]
3.1.2. Lấy mẫu chùm (cluster sampling)
Phép lấy mẫu (3.1.12) trong đó mẫu ngẫu nhiên (3.1.8) của các chùm (3.1.1) được chọn và tất cả các đơn vị mẫu (3.1.13) tạo thành chùm bao gồm trong mẫu (3.1.11).
TCVN 8244-2:2010 (ISO 3534-2:2006), 1.3.9]
3.1.3. Xáo trộn (derangement)
Hoán vị hoàn toàn (complete permutation)
Hoán vị các thành phần trong đó không một thành phần nào còn giữ nguyên vị trí ban đầu trong tập hợp (ví dụ {3, 1, 2} là hoán vị của {1, 2, 3}).
3.1.4. Lô (lot)
Bộ phận xác định của tổng thể (3.1.6) cấu thành trong các điều kiện về cơ bản giống với tổng thể xét về mục đích lấy mẫu (3.1.12).
CHÚ THÍCH: Ví dụ, mục đích lấy mẫu có thể để xác định khả năng chấp nhận lô hoặc để ước lượng giá trị trung bình của một đặc trưng cụ thể.
TCVN 8244-2:2010 (ISO 3534-2:2006), 1.2.4]
3.1.5. Lấy mẫu nhiều tầng (multistage sampling)
Phép lấy mẫu (3.1.12) trong đó mẫu (3.1.11) được chọn theo tầng, các đơn vị mẫu (3.1.13) tại mỗi tầng được lấy từ đơn vị mẫu lớn hơn được chọn ở tầng trước đó.
CHÚ THÍCH: Lấy mẫu nhiều tầng khác với lấy mẫu nhiều lần. Lấy mẫu nhiều lần là lấy mẫu theo nhiều tiêu chí đồng thời.
TCVN 8244-2:2010 (ISO 3534-2:2006), 1.3.10]
3.1.6. Tổng thể (population)
TCVN 8244-2:2010 (ISO 3534-2:2006), 1.2.1]
3.1.7. Lấy mẫu ngẫu nhiên giả độc lập (pseudo-independent random sampling)
Lấy mẫu (3.1.12) trong đó mẫu (3.1.11) gồm n đơn vị mẫu (3.1.13) được lấy từ tổng thể (3.1.6) theo bảng số ngẫu nhiên hoặc thuật toán trên máy tính được thiết kế sao cho mỗi tổ hợp có thể có của n đơn vị mẫu có một xác suất được lấy cụ thể (xem thêm 4.4).
3.1.8. Mẫu ngẫu nhiên (random sample)
Mẫu (3.1.11) chọn bằng phép lấy mẫu ngẫu nhiên (3.1.9).
TCVN 8244-2:2010 (ISO 3534-2:2006), 1.2.25]
3.1.9. Lấy mẫu ngẫu nhiên (random sampling)
Phép lấy mẫu (3.1.12) trong đó có một mẫu (3.1.11) gồm n đơn vị mẫu (3.1.13) được lấy từ một tổng thể (3.1.6) sao cho mỗi tổ hợp có thể có của n đơn vị mẫu có một xác suất được lấy cụ thể.
TCVN 8244-2:2010 (ISO 3534-2:2006), 1.3.5]
3.1.10. Ngẫu nhiên hóa (randomization)
Quá trình nhờ đó tập hợp các cá thể được đặt theo một trật tự ngẫu nhiên.
CHÚ THÍCH: Nếu từ một tổng thể (3.1.6) gồm các số tự nhiên từ 1 đến n, các số được lấy ngẫu nhiên (nghĩa là theo cách thức tất cả các số đều có cơ hội được lấy như nhau), từng số một, lần lượt, không hoàn lại, cho đến khi hết tổng thể, các số này được gọi là lấy “theo thứ tự ngẫu nhiên”.
Nếu n số này được liên kết trước với n đơn vị riêng biệt hay n xử lý riêng biệt mà sau đó được sắp xếp theo thứ tự các số được lấy thì thứ tự của các đơn vị hay xử lý đó được coi là được ngẫu nhiên hóa.
3.1.11. Mẫu (sample)
Tập hợp con của tổng thể (3.1.6) bao gồm một hoặc nhiều đơn vị mẫu (3.1.13).
TCVN 8244-2:2010 (ISO 3534-2:2006), 1.2.17]
3.1.12. Lấy mẫu (sampling)
Hoạt động lấy hoặc thành lập một mẫu (3.1.11).
TCVN 8244-2:2010 (ISO 3534-2:2006), 1.3.1]
3.1.13. Đơn vị mẫu (sampling unit)
Đơn vị (unit)
Một trong các thành phần riêng lẻ hợp thành tổng thể (3.1.6).
CHÚ THÍCH 1: Đơn vị mẫu có thể gồm một hoặc nhiều cá thể, ví dụ một bao diêm, nhưng sẽ bao hàm một liên kết quả thử.
CHÚ THÍCH 2: Đơn vị mẫu có thể gồm các cá thể rời rạc hoặc một lượng vật liệu dạng đống xác định.
TCVN 8244-2:2010 (ISO 3534-2:2006), 1.2.14]
3.1.14. Lấy mẫu có hoàn lại (sampling with replacement)
Lấy mẫu (3.1.12) trong đó mỗi đơn vị mẫu (3.1.13) được lấy ra, quan trắc, rồi được trả về tổng thể (3.1.6) trước khi lấy đơn vị mẫu tiếp theo.
TCVN 8244-2:2010 (ISO 3534-2:2006), 1.3.15]
3.1.15. Lấy mẫu không hoàn lại (sampling without replacement)
Lấy mẫu (3.1.12) trong đó mỗi đơn vị mẫu (3.1.13) chỉ được lấy ra từ tổng thể (3.1.6) một lần mà không được trả về tổng thể đó.
TCVN 8244-2:2010 (ISO 3534-2:2006), 1.3.16]
3.1.16. Giá trị xuất phát (seed)
Trị số hoặc tập hợp các giá trị để khởi đầu một thuật toán lấy mẫu ngẫu nhiên giả độc lập (3.1.7) hoặc để thiết lập điểm bắt đầu trong bảng số ngẫu nhiên.
3.1.17. Mẫu ngẫu nhiên đơn giản (simple random sample)
Mẫu (3.1.11) được chọn bằng cách lấy mẫu ngẫu nhiên đơn giản (3.1.18).
TCVN 8244-2:2010 (ISO 3534-2:2006), 1.2.24]
3.1.18. Lấy mẫu ngẫu nhiên đơn giản (simple random sampling)
Phép lấy mẫu (3.1.12) trong đó có một mẫu(3.1.11) gồm n đơn vị mẫu (3.1.13) được lấy từ một tổng thể (3.1.6) sao cho tất cả các tổ hợp có thể có của n đơn vị mẫu có cùng xác suất được lấy ra.
TCVN 8244-2:2010 (ISO 3534-2:2006), 1.3.4]
3.1.19. Lấy mẫu phân lớp (stratified sampling)
Lấy mẫu (3.1.12) sao cho các phần mẫu (3.1.11) được lấy từ lớp (3.1.21) khác nhau và mỗi lớp được lấy ít nhất là một đơn vị mẫu (3.1.13).
TCVN 8244-2:2010 (ISO 3534-2:2006), 1.3.6]
3.1.20. Lấy mẫu ngẫu nhiên đơn giản phân lớp (stratified simple random sampling)
Lấy mẫu ngẫu nhiên đơn giản (3.1.18) từ mỗi lớp (3.1.21).
TCVN 8244-2:2010 (ISO 3534-2:2006), 1.3.7]
3.1.21. Lớp (stratum)
Tổng thể con tách biệt và đầy đủ được xem là đồng nhất hơn về các đặc trưng nghiên cứu so với toàn bộ tổng thể (3.1.6).
TCVN 8244-2:2010 (ISO 3534-2:2006), 1.2.29]
3.2. Ký hiệu
Tiêu chuẩn này áp dụng dấu và ký hiệu toán học trong TCVN 7870-2 (ISO 80000-2) và các ký hiệu sau:
di con số thứ i hoặc giá trị mặt của đồng xu hay xúc sắc
N cỡ lô
n cỡ mẫu
ni cỡ của mẫu thứ i
U biến thực ngẫu nhiên phân bố đều trên phạm vi mở (0, 1)
![]() giá trị thứ i của biến
giá trị thứ i của biến ![]()
j! j giai thừa
éz ù hàm trần nguyên của z (trả về số nguyên nhỏ nhất lớn hơn hoặc bằng giá trị thực z)
ë z û hàm sàn nguyên của z (trả về phần nguyên của giá trị thực z)
4.1. Lấy mẫu ngẫu nhiên là điều kiện tiên quyết để áp dụng đúng hầu hết các phương án lấy mẫu trong ứng dụng công nghiệp. Tương tự, ngẫu nhiên hóa, sử dụng các nguyên tắc lấy mẫu ngẫu nhiên, là không thể thiếu được khi thực hiện các thiết kế thực nghiệm, vì nó làm tăng hiệu lực nội tại của thực nghiệm, cho phép sử dụng các phương pháp thống kê trong giải thích các kết quả thực nghiệm. Mục tiêu của lấy mẫu ngẫu nhiên là cung cấp phương tiện áp dụng các kết quả của lý thuyết xác suất vào các vấn để thực tiễn, trong khi tránh được mọi dạng độ chệch bất kỳ. Mục tiêu này không đạt được khi sử dụng các loại lấy mẫu nhất định khác. Ví dụ, lấy mẫu dựa trên các khái niệm như trực giác hay đánh giá của cá nhân, tính lộn xộn, hoặc theo hạn ngạch đều có độ chệch vốn có và kết quả dẫn đến sai lỗi nghiêm trọng trong quá trình ra quyết định mà không có điều kiện đánh giá rủi ro. Lấy mẫu ngẫu nhiên đồng xác suất nhằm loại trừ độ chệch như vậy bằng cách đảm bảo rằng mỗi đơn vị trong lô có cùng một xác suất được chọn (lấy mẫu có hoàn lại) hay, nói cách khác, mọi mẫu có thể trong cỡ mẫu cho trước lấy từ một lô có cùng xác suất được chọn (lấy mẫu không hoàn lại).
4.2. Trong phương án lấy mẫu ngẫu nhiên đồng xác suất có hoàn lại, xác suất một đơn vị cụ thể trong lô gồm N đơn vị được chọn ở lần lấy cho trước bất kỳ luôn là 1/N. Có Nn ngẫu nhiên theo thứ tự có thể có của n đơn vị từ N đơn vị và, đầy đủ là, có (N + n – 1)! / [n! (N – 1)!] mẫu ngẫu nhiên không theo thứ tự khác nhau có thể gồm n đơn vị từ N đơn vị (xem chú thích bên dưới).
Theo phương án lấy mẫu ngẫu nhiên đơn giản không hoàn lại, xác suất một đơn vị trong lô được chọn ở lần lấy trước là 1/N đối với lần lấy đầu tiên, 1/(N – 1) đối với lần lấy thứ hai, 1/(N – 2) đối với lần thứ ba, và cứ tiếp tục như vậy. Nếu n đơn vị được chọn ngẫu nhiên từ lô gồm N đơn vị mà không hoàn lại, khi đó mỗi tổ hợp n đơn vị có cùng một xác suất lựa chọn với mọi tổ hợp N đơn vị khác lấy n đơn vị mỗi lần. Số lượng mẫu gồm n đơn vị ngẫu nhiên không theo thứ tự xác suất khác nhau từ lô gồm N đơn vị là N!/(N-1)!, tương đương với số lượng tổ hợp gồm N đơn vị lấy n đơn vị mỗi lần . Điều đáng lưu ý khác là số lượng mẫu ngẫu nhiên theo thứ tự gồm n đơn vị được lấy không hoàn lại từ lô gồm N đơn vị là N! (N – n)! tương đương với số hoán vị có thể có gồm N đơn vị lấy n đơn vị mỗi lần. Cần chú ý là việc lấy mẫu ngẫu nhiên không hoàn lại là phương án lấy mẫu phổ biến nhất được sử dụng trong các ứng dụng lấy mẫu chấp nhận.
CHÚ THÍCH: Trong lấy mẫu có hoàn lại trên cơ sở mẫu gồm 3 đơn vị trong 5 đơn vị, danh mục {1, 1, 2}, {1, 2, 1} và {2, 1, 1} sẽ khác khi xét về thứ tự (và về kỹ thuật gọi là đa tập hợp) nhưng giống nhau nếu không xét đến thứ tự.
4.3. Mục tiêu của lấy mẫu ngẫu nhiên chỉ có thể đạt được bằng việc gắn với các quy trình chặt chẽ được thiết kế kỹ càng để đạt được mục đích của định nghĩa. Nhiều phương pháp được trình bày trong tiêu chuẩn này để thực thi mục tiêu này. Cụ thể là các phương pháp dùng thiết bị cơ khí giả định rằng đồng xu và xúc sắc không có độ chệch, được thiết kế sao cho mỗi mặt có cùng một xác suất xuất hiện trong quá trình ném hay tung và cách thức tung hay ném được thực hiện để không gây ra độ chệch. Hơn nữa, do những khác biệt lớn trong việc áp dụng nội tại các phương pháp lấy mẫu ngẫu nhiên trong máy tính cũng như hệ điều hành máy tính, ngôn ngữ lập trình và phần mềm (xem tài liệu tham khảo [9], [10], [12] và [13] về thông tin thêm), nên tiêu chuẩn này lựa chọn phương pháp tạo mẫu ngẫu nhiên bằng máy tính cầm tay. Ngoài ra,cần lưu ý là tất cả các phương pháp dưới đây đòi hỏi rằng mỗi đơn vị riêng rẽ trong lô được kết hợp trước với một số nhất định từ 1 đến N, sao cho các đơn vị lấy mẫu xác định là kết quả của phương pháp lấy mẫu ngẫu nhiên có thể thu được một cách rõ ràng từ lô đó.
4.4. Cuối cùng, để giảm khó khăn trong việc trình bày, tính từ “giả độc lập” sẽ thường được bỏ bớt khi đề cập đến quy trình hay phương pháp lấy mẫu ngẫu nhiên như vậy (xem tài liệu tham khảo [8]). Hơn nữa, tính từ “ngẫu nhiên” sẽ được sử dụng thường xuyên với nghĩa là danh từ mà nó bổ nghĩa (thường là số hoặc phép hoán vị) là đầu ra của quá trình tạo ra ngẫu nhiên số hay phép hoán vị đó. Ngoài ra, khi có các ví dụ, cỡ mẫu liên quan được giữ ở con số nhỏ với mục tiêu minh họa một cách đơn giản những khái niệm liên quan.
5. Lấy mẫu ngẫu nhiên – Phương pháp dùng thiết bị cơ khí
5.1. Phương pháp bình
5.1.1. Đặt N vật giống hệt nhau nhưng được đánh số khác nhau (ví dụ: vé, đồng tiền hay quả bóng) vào một chiếc bình để thể hiện rõ ràng mỗi trong số N đơn vị trong lô đó rồi trộn kỹ các đồ vật đó.
5.1.2. Đối với lấy mẫu không hoàn lại, nhắm mắt chọn các đồ vật trong bình, từng vật một mà không trả lại vào bình rồi trộn lại các vật giữa các lần lấy liên tiếp, cho đến khi có được n đơn vị lấy mẫu mong muốn.
CHÚ THÍCH: Phương pháp này thường được sử dụng bởi các công ty xổ số.
5.1.3. Đối với lấy mẫu có hoàn lại, nhắm mắt chọn các đồ vật trong bình, từng vật một rồi trả lại bình sau mỗi lần lấy và trộn kỹ lại các vật giữa các lần lấy liên tiếp, cho đến khi có được n đơn vị lấy mẫu mong muốn. Sử dụng phương pháp này, cùng một đơn vị có thể xuất hiện trong mẫu nhiều hơn một lần.
5.2. Phương pháp đồng xu hay xúc sắc
5.2.1. Xác định số m đồng xu hay xúc sắc (hoặc lượt thả đồng xu hay xúc sắc) yêu cầu, trong đó N là cỡ lô và k là số mặt của vật được sử dụng, theo công thức sau:
![]() = élogeN/logekù
= élogeN/logekù
5.2.2. Khi sử dụng đồng xu hoặc xúc sắc, gắn kết rõ từng đồng xu hay xúc sắc với một vị trí cụ thể trong thứ tự giải thích các số di. Trường hợp sử dụng một đồng xu hay một xúc sắc, ấn định kết quả của lần tung hay thả đầu tiên với số có ý nghĩa nhất dm, lần tung hay thả thứ hai với số có nghĩa tiếp theo dm-1, và tiếp tục như vậy.
5.2.3. Thả đồng xu hay tung xúc sắc rồi ghi lại m kết quả theo thứ tự di. Chuyển kết qủa sang số nguyên thập phân theo công thức sau:
![]()
5.2.4. Lặp lại bước 5.2.3, loại tất cả các giá trị vượt quá N và, trong trường hợp lấy mẫu không hoàn lại, tất cả các giá trị đã được chọn, cho đến khi đạt được n đơn vị mẫu mong muốn.
VÍ DỤ 1: Kiểm tra viên mong muốn có được mẫu ngẫu nhiên gồm 4 đơn vị từ lô có 20 đơn vị và có sẵn một đồng xu. Từ bước 5.2.1, xác định được rằng cần m = 5 lần tung đồng xu để có được mỗi số ngẫu nhiên. Ấn định trước rằng giá trị mặt sấp là 1 và giá trị mặt ngửa là 2. Thứ tự những lần tung đầu tiên có được đa tập hợp {1, 2, 1, 2, 2}, thông qua bước 5.2.3 bằng 1 + (0)24 + (1)23 + (0)22 + (1)21 + (1)20 = 12. Ba lượt tung tiếp theo cho các tập hợp {1, 2, 2, 2, 1}, {1, 1, 2, 2, 1} và {2, 2, 1, 2, 2} tương ứng bằng 15, 7 và 28. Vì giá trị 28 vượt quá cỡ lô nên cần loại bỏ và các lượt tung tiếp theo cần được thực hiện cho đến khi thu được một số hợp lệ nữa để hoàn thành việc lấy mẫu ngẫu nhiên.
VÍ DỤ 2: Cần mẫu ngẫu nhiên gồm 4 đơn vị từ một lô gồm 50 đơn vị và kiểm tra viên có nhiều xúc sắc sáu mặt có màu sắc khác nhau. Từ bước 5.2.1, xác định được cần m = 3 con xúc sắc để thu được từng số ngẫu nhiên. Kiểm tra viên chọn xúc sắc màu xanh da trời, xanh lá cây và đỏ rồi xếp chúng theo cùng thứ tự ý nghĩa nhất đến ít ý nghĩa nhất. Tuy nhiên, kiểm tra công thức ở 5.2.3 cho thấy bằng chứng là các số nằm trong phạm vi hợp lệ từ 1 đến 50 sẽ chỉ có được khi mặt xúc sắc đầu tiên là 1 hoặc 2. Kết quả là, hiệu quả nhất định có thể đạt được bằng cách đặt các giá trị mặt cao hơn của xúc sắc màu xanh da trời là 1 hoặc 2 mà không làm méo xác suất kết quả. Kiểm tra viên quyết định trước đối với giá trị mặt lẻ trên xúc sắc xanh da trời coi là 1 và mặt giá trị chẵn coi là 2. Vòng đầu tiên cho tập hợp {3, 3, 4}, thông qua bước 5.2.3 bằng 1 + (2)62 + (2)61 + (3)60 = 88, giá trị này quá lớn nhưng khi chuyển thành {1, 3, 4} bằng 16. Ba vòng tiếp theo cho {6, 1, 3} (chuyển thành {2,1 ,3}), {5, 6, 6} (chuyển thành {1, 6, 6,}) và {2, 5, 5}, tương ứng bằng 39, 36 và 65. Vì giá trị 65 vượt quá cỡ lô nên cần loại bỏ và cần thực hiện những lần bổ sung cho đến khi thu được một giá trị hợp lệ nữa để hoàn thành lấy mẫu ngẫu nhiên.
VÍ DỤ 3: Tình huống tương tự như trong Ví dụ 2 nhưng lần này kiểm tra viên thấy rằng ba xúc sắc sẽ tạo ra các số trong phạm vi từ 1 đến 63 = 216 mà cỡ lô chỉ là 50. Kiểm tra viên quyết định trước sẽ ánh xạ tất cả các kết quả từ 1 đến 200 lên dải tần từ 1 đến 50 và loại bỏ mọi kết quả lớn hơn 200 nhằm tránh bóp méo xác suất đầu ra. Bốn lượt tung tương tự như ở ví dụ trước được đánh giá theo phương án ánh xạ này. Các đa tập hợp {3, 3, 4}, {6, 1, 3}, {5, 6, 6} và {2, 5, 5} bằng 88, 183, 180 và 65. Các số này được trừ đi cho bội số của 50 cho đến khi chúng nằm trong phạm vi từ dãy 1 đến 50 (nếu thu được giá trị 0 thì giải thích như N), có được các giá trị mẫu tương ứng là 38, 33, 30 và 15. Cỡ mẫu là 4 đơn vị đã thu được nên không cần tiếp tục tung xúc sắc nữa. Chú ý là, về mặt toán học, quá trình ánh xạ này tương đương với việc áp dụng công thức v2 = 1 + (v1 – 1) mô đun N, trong đó v1 là giá trị ban đầu còn v2 là giá trị được ánh xạ vào dải mong muốn.
6. Lấy mẫu ngẫu nhiên giả độc lập – Phương pháp bảng số
6.1. Bảng số ngẫu nhiên
Hai bảng số ngẫu nhiên được cung cấp trong Phụ lục A. Mỗi bảng số gồm 3 600 số ngẫu nhiên từ 0 đến 9, sắp xếp thành 60 hàng và 60 cột. Việc sử dụng được mô tả tóm tắt dưới đây và nêu chi tiết hơn trong Phụ lục A.
CHÚ THÍCH: Các con số trong bảng tương tự trực tiếp với các giá trị mặt của xúc sắc 10 mặt tung lặp lại và ghi được. Số chữ số m cần thiết cho ứng dụng lấy mẫu tương ứng với số lần tung xúc sắc.
6.2. Phương pháp cơ bản
6.2.1. Xác định số chữ số m cần thiết để thể hiện cỡ lô N. Trường hợp cỡ lô có lũy thừa 10, bỏ qua con số đầu trong cỡ lô đó và giải thích rằng các con số “không” còn lại bằng giá trị cỡ lô (ví dụ nếu N = 1 000, giải thích giá trị 000 là 1 000).
6.2.2. Chọn ngẫu nhiên một điểm bắt đầu (nghĩa là giá trị hàng và cột) trong bảng sử dụng phương pháp mô tả ở A.2.2.
6.2.3. Đọc con số kết quả cùng với các số m – 1 ở bên phải như một số và ghi lại giá trị đó. Trường hợp các con số bên phải vượt quá hàng thứ 60 thì coi các cột 1, 2, … tương ứng là cột 61, 62, …
6.2.4. Tăng giá trị của hàng thêm một, lặp lại bước 6.2.3 rồi ghi lại giá trị đó. Trường hợp giá trị của hàng vượt quá hàng thứ 60 thì coi hàng 1 là hàng thứ 61 và tăng giá trị cột đó lên m chữ số.
6.2.5. Lặp lại bước 6.2.4, bỏ qua tất cả các giá trị vượt quá N và, trong trường hợp lấy mẫu không hoàn lại, tất cả các giá trị đã được chọn, cho đến khi thu được số đơn vị lấy mẫu n mong muốn.
VÍ DỤ: Người đánh giá mong muốn chọn một mẫu ngẫu nhiên gồm 5 đơn vị từ một lô 200 đơn vị. Điểm bắt đầu ngẫu nhiên được xác định bằng các lần tung đồng xu là hàng 57 và cột 59, quyết định sử dụng Bảng A.1. Vì N nhỏ so với giá trị lớn nhất có thể thể hiện bằng 3 chữ số (nghĩa là 1 000) nên người đánh giá quyết định ánh xạ kết quả của dải từ 1 đến 1 000 lên dải từ 1 đến 200. Kết quả là năm số sau: 848, 670, 902, 034 và 518. Giá trị mẫu chuyển đổi trở thành 48, 70, 102, 34 và 118.
7. Lấy mẫu ngẫu nhiên giả độc lập – Phương pháp máy tính
7.1. Tổng quan
7.1.1. Tiêu chuẩn này sử dụng hệ thống thuật toán cụ thể đề cập trong các tài liệu tham khảo [1], [7] và [13]. Các thuật toán này được thiết kế có các tính chất hóa học và thống kê cần thiết cho lấy mẫu ngẫu nhiên cũng như có thể linh hoạt áp dụng trong các ngôn ngữ lập trình khác nhau trên các nền tảng máy tính khác nhau đồng thời tạo thuận lợi cho việc kiểm tra và đánh giá các giá trị mẫu được chọn cần thiết cho mục đích quy định. Ví dụ thực thi các phần chương trình chính được cho trong Phụ lục B sử dụng ngôn ngữ lập trình C.
7.1.2. Hệ thống các thuật toán liên quan gồm hai hệ con chính:
a) thuật toán khởi tạo tùy chọn tự động đưa ra số nguyên ban đầu giả ngẫu nhiên dựa trên thời gian trôi qua kể từ ngày tháng chuẩn; và
b) bộ tạo số ngẫu nhiên.
7.1.3. Đối với mục đích kiểm tra hay đánh giá, thuật toán khởi tạo tùy chọn đề cập ở điểm a) của 7.1.2 và mô tả 7.2 có thể bỏ qua với một giá trị xuất phát nhập bằng tay. Giá trị này cần nằm trong dãy số nguyên tử từ 1 đến và bao gồm cả 2 147 483 398. Bản sao giá trị đầu vào này được giữ lại để lưu hồ sơ khi cần. Tuy nhiên, trong sử dụng chung cho các ứng dụng kiểm soát chất lượng và thiết kế thực nghiệm không nên thường xuyên bỏ qua tùy chọn tạo giá trị xuất phát ngẫu nhiên tự động mà nên là tùy chọn mặc định trong thực tế.
CHÚ THÍCH: Trình bày về các bước của các thuật toán trong điều này được để ở định dạng toán học hơn nhằm hỗ trợ cho việc lập trình. Mã lập trình có các tham chiếu điều được nêu trong Phụ lục B để bổ trợ cho việc áp dụng điều này.
7.2. Thuật toán khởi tạo
7.2.1. Thuật toán khởi tạo bao gồm:
a) thuật toán tính thời gian trôi qua, tham chiếu đến ngày tháng và thời gian quá khứ cố định, và
b) thuật toán tạo số ngẫu nhiên dựa trên phân bố đều, gọi là số ngẫu nhiên của thời gian dựa trên đầu ra của mục a) ở trên, để thu được giá trị xuất phát ngẫu nhiên dựa trên đầu vào theo thời gian.
7.2.2. Thuật toán dưới đây xác định số giây trôi qua tính từ 00:00:00 01-01-2000 đến ngày tháng và thời gian hiện tại.
a) Tìm ngày tháng và thời gian của hệ thống máy tính theo biến dạng chuỗi, lưu bản sao biến này vào hồ sơ và sau đó phân tích chuỗi thành các thành phần thời gian (nghĩa là giây, phút, giờ, ngày, tháng và năm).
b) Tính số ngày tròn trôi qua de từ điểm thời gian chuẩn, sử dụng trị số năm đầy đủ bốn con số y, tháng m1 và ngày d của ngày tháng hiện tại xử lý như sau:
nếu m1 < 3 thì lấy m1 + 12 và lấy y = y – 1
de = d + ë(153 m1 – 457) / 5û + 365 y + ëy / 4û - ëy / 100û + ë y / 400û - 730 426
CHÚ THÍCH: Công thức cho de có thể đơn giản hóa một chút đối với năm theo lịch đến và kể cả 2099 bằng cách thay số hạng ëy / 4û bằng “ – 730 441”.
c) Tính tổng số giây se trôi qua từ ngày tháng quy chiếu sử dụng con số thu được ở bước b) và thời gian của ngày (ở dạng 24 giờ “giờ:phút:giây”) tìm được trong biến chuỗi ở bước a) theo công thức sau:
se = 86 400 de + 3 600 h+ 60 m2 + s
trong đó h, m2 và s tương ứng là giờ, phút và giây.
CHÚ THÍCH 1: Một số ngôn ngữ lập trình có hàm dựng sẵn để thực hiện tính toán trực tiếp se. Các hàm nội tại như vậy cần được xác nhận hiệu lực trước khi sử dụng để đảm bảo ảnh hưởng của năm nhuận và thời gian ghi ban ngày được xử lý thích hợp.
CHÚ THÍCH 2: Trong ứng dụng 32 bit của thuật toán này, giá trị se sẽ tăng thời gian đến điểm gây tràn tính toán. Cần chú ý khi lập trình để đảm bảo giá trị đầu vào luôn được ánh xạ lên từ 1 đến và bao gồm cả 2 147 483 398.
d) Giá trị ở bước c) là giá trị khởi tạo cho bộ tạo giá trị ngẫu nhiên và được dùng để thu giá trị cuối cùng. Bản sao giá trị này được ghi vào biến riêng để lưu hồ sơ khi cần.
e) Số thời gian j mà bộ tạo số ngẫu nhiên sau đó được yêu cầu là một số nguyên ngẫu nhiên từ 1 đến và bao gồm cả 100, dựa trên hai con số ít có nghĩa nhất của giá trị thu được ở bước c) cộng thêm 1, được thể hiện như sau:
j = se – 100 ëse / 100û + 1
7.2.3. Bộ tạo số ngẫu nhiên dùng cho thuật toán tạo giá trị xuất phát tự động (hàm khởi tạo) có dạng quan hệ truy hồi đồng dạng tuyến tính:
a) xi+1 = 40 692 ![]() mod 2 147 483 399,
mod 2 147 483 399,
có thể thực hiện trên máy tính có khả năng xử lý số nguyên 32 bit qua các bước sau đây:
b) ![]() ë
ë![]() / 52 774û ;
/ 52 774û ;
c) ![]() +1 = 40 692 (
+1 = 40 692 (![]() - 52 774 k) – 3 791 k;
- 52 774 k) – 3 791 k;
d) Nếu ![]() +1 < 0 thì lấy
+1 < 0 thì lấy ![]() +1 =
+1 = ![]() +1 + 2 147 483 399.
+1 + 2 147 483 399.
7.2.4. Tạo giá trị xuất phát cho thuật toán lấy mẫu ngẫu nhiên bằng cách ấn định kết quả ở điểm c) 7.2.2 cho xi rồi gọi công thức ở 7.2.3 j lần cho mỗi bước 7.2.2 e), mỗi lần thay xi bằng xi+1 cho đến khi thực hiện hết số lần gọi yêu cầu.
7.2.5. Giá trị cuối cùng của xi+1 thu được từ bước 7.2.4 là số nguyên ngẫu nhiên từ 1 đến và bao gồm cả 2 147 483 398 và dùng làm giá trị xuất phát ban đầu cho thuật toán lấy mẫu ngẫu nhiên mô tả ở 7.3 [cụ thể là giá trị yi ở bước b) của 7.3.6]. Bản sao giá trị này được ghi vào biến riêng để lưu hồ sơ khi cần.
7.3. Thuật toán tạo số ngẫu nhiên
7.3.1. Thuật toán tạo số ngẫu nhiên bao gồm
a) một dãy xáo trộn được tạo bởi thuật toán tạo số ngẫu nhiên phân bố đều và,
b) tổ hợp, thuật toán tạo số ngẫu nhiên phân bố đều.
7.3.2. Tạo dãy A gồm 32 phần tử dùng như phương tiện xáo trộn đầu ra của thuật toán lấy mẫu ngẫu nhiên.
7.3.3. Bộ tạo số ngẫu nhiên dưới đây được dùng để tạo dãy xáo trộn:
a) xi+1 = 40 014 xi mod 2 147 483 563,
có thể được thực hiện trên máy tính 32 bit qua các bước sau đây:
b) k = ë ![]() / 53 668û;
/ 53 668û;
c) xi+1 = 40 014 (![]() - 53 668 k) – 12 211 k;
- 53 668 k) – 12 211 k;
d) Nếu xi+1 < 0 thì lấy xi+1= xi+1 + 2 147 483 563.
7.3.4. Khởi tạo dãy A bằng cách ấn định kết quả ở 7.1.3 hoặc 7.2.5 cho xi rồi gọi bộ tạo giá trị nêu trong 7.3.3 a) 40 lần, mỗi lần gọi thay xi bằng xi+1, loại bỏ 8 giá trị đầu tiên và sau đó ấn định mỗi trong số 32 giá trị đầu ra còn lại của xi+1 cho dãy đó theo thứ tự đảo (nghĩa là phần tử 32 xuống đến phần tử 1).
7.3.5. Đặt phần tử 1 của dãy A (nghĩa là A[1]) là giá trị khởi tạo k cho tổ hợp thuật toán tạo số ngẫu nhiên.
7.3.6. Tổ hợp bộ tạo số ngẫu nhiên dùng để tạo mẫu ngẫu nhiên có dạng tổ hợp quan hệ tái diễn đồng dạng tuyến tính và các bước xác định chỉ số dãy sau đây:
a) xi+1 = 40 014 ![]() mod 2 147 483 563,
mod 2 147 483 563,
b) yi+1 = 40 692 yi mod 2 147 483 399,
c) J = ë32 k / 2 147 483 563û + 1;
d) k = A[J] – yi+1;
e) A[J] = xi+1;
f) Nếu k < 1 thì lấy k = k + 2 147 483 562.
CHÚ THÍCH: Hai bộ tạo số ngẫu nhiên ở trên được mô tả trong 7.2.3 và 7.3.3 (tham khảo các điều con nếu cần các ứng dụng tương đương 32 bit).
7.3.7. Thuật toán ở 7.3.6 được bắt đầu bằng việc đặt xi+1 theo giá trị cuối cùng của xi+1 từ 7.3.4 và đặt yi theo giá trị tham chiếu ở 7.2.5. Các giá trị xi+1 và yi+1 dùng làm giá trị tiếp theo của xi và yI cho tất cả các lần gọi sau của thuật toán. Chỉ số ngẫu nhiên J cho dãy xáo trộn A được tính bằng cách sử dụng giá trị của k (ban đầu từ 7.3.5) và hiệu của A[J] và yi+1 được ấn định cho k, trong khi A[J] được cập nhật với xi+1. Cuối cùng giá trị của k được thay đổi nếu cần để tạo ra giá trị dương.
7.3.8. Đầu ra của thuật toán lấy mẫu ngẫu nhiên là giá trị k, là số ngẫu nhiên từ 1 đến và bao gồm cả 2 147 483 562, được chỉnh tỷ lệ như biến thực phân bố đều chuẩn hóa U trong dải tần từ 0 đến 1, không bao gồm giá trị đầu mút của dải này, như sau: U = k / 2 147 483 563.
7.3.9. Đầu ra của 7.3.8 có thể được chỉnh tỷ lệ là biến nguyên phân bố đều L trong dải tần từ 1 đến N, bao gồm cả N, như sau: L = ëN Uû + 1.
7.3.10. Để tạo ra mẫu ngẫu nhiên, lặp lại các bước từ 7.3.6 đến 7.3.9 cho đến khi thu được số giá trị ngẫu nhiên cần thiết.
7.4. Hồ sơ đánh giá
Khi có yêu cầu duy trì hồ sơ cho việc đánh giá của cơ quan chịu trách nhiệm hay cơ quan có thẩm quyền, thì ghi lại cỡ lô và cỡ mẫu.
Ngoài ra, đối với các thuật toán, ghi lại giá trị xuất phát nhập bằng tay theo 7.1.3 hoặc nếu sử dụng bộ tạo giá trị xuất phát ngẫu nhiên thì ghi lại.
a) ngày và thời gian của hệ thống máy tính sử dụng để tính giá trị xuất phát ban đầu,
b) giá trị của số khởi tạo theo 7.2.2 d) và
c) giá trị của số khởi tạo cuối cùng theo 7.2.5.
8. Áp dụng cho tình huống lấy mẫu phổ biến
8.1. Khái quát
8.1.1. Điều này đưa ra thuật toán dùng cho nhiều phương án lấy mẫu ngẫu nhiên phù hợp với nhiều tình huống thực tiễn khác nhau.
8.1.2. Xuyên suốt điều này, U được xác định là biến ngẫu nhiên thực, phân bố đều trong dải tần từ 0 đến 1, không bao gồm các giá trị đầu mút của dải, như cung cấp bởi thuật toán ở 7.3. Nếu sử dụng nguồn khác cho U và đầu ra được biết bao gồm 1 nhưng không bao gồm 0 là giá trị đầu mút của dải thì đặt U bằng 1 – U. Nếu nguồn khác của U bao gồm 0 và 1 là giá trị đầu mút của dải thì giá trị 1 cần được chặn và loại ra.
8.2. Số nguyên ngẫu nhiên trong dải
Số nguyên ngẫu nhiên K trong dải từ M đến và gồm cả N có thể được tạo ra theo thuật toán dưới đây.
a) Tạo giá trị thực ngẫu nhiên U.
b) Đặt K bằng M + ëU (N – M + 1)û.
8.3. Hoán vị ngẫu nhiên
Đối với dãy A với N phần tử riêng biệt, phép hoán vị ngẫu nhiên N đơn vị lấy n mỗi lần có thể được tạo ra theo thuật toán xáo trộn dưới đây.
a) Ẩn định N giá trị chỉ số phần tử riêng rẽ theo thứ tự ban đầu đến A[1:N].
b) Đặt J bằng 1.
c) Tạo số nguyên ngẫu nhiên K trong dải tần từ J đến và bao gồm cả N.
d) Đổiv A[J] và A[K].
e) Tăng J thêm 1.
f) Nếu J nhỏ hơn hoặc bằng n thì đi tiếp bước c).
g) Thu được hoán vị ngẫu nhiên từ các giá trị n đầu tiên của dãy A.
8.4. Trộn ngẫu nhiên
Đối với dãy A với N phần tử riêng biệt, trộn ngẫu nhiên N đơn vị có thể được tạo ra theo thuật toán dưới đây.
a) Ấn định N giá trị chỉ số phần tử riêng rẽ theo thứ tự ban đầu đến A[1:N] và sao chép vào dãy B[1:N].
b) Sử dụng dãy B tạo xáo trộn ngẫu nhiên N đơn vị lấy N (nghĩa là tất cả) đồng thời, sử dụng phương pháp nêu ở 8.3.
c) So sánh sự ngang bằng các phần tử từ 1 đến N của dãy A và dãy B
d) Nếu phần tử bất kỳ của dãy B bằng với phần tử đối ứng ở dãy A thì dừng việc so sánh và đi tiếp bước b).
e) Thu được phép trộn ngẫu nhiên từ dãy B.
CHÚ THÍCH: Thuật toán này có thể được thực hiện hiệu quả hơn ở bước b) và c) bằng cách so sánh phần tử A[J] với phần tử B[J] ngay khi xác định được B[J] chứ không đợi đến khi hoán vị hết toàn bộ dãy B.
8.5. Lấy mẫu ngẫu nhiên có hoàn lại
Mẫu ngẫu nhiên đơn gồm n đơn vị từ lô N đơn vị có thể được tạo ra có hoàn lại theo thuật toán dưới đây.
a) Tạo số nguyên ngẫu nhiên K trong dải từ 1 đến và bao gồm cả N.
b) Lặp lại bước a) cho đến khi thu được n giá trị của K.
CHÚ THÍCH: Có thể áp dụng lặp lại phương pháp này để thu được số lượng mẫu bất kỳ với cỡ mẫu bất kỳ. Nếu giá trị thu được của mẫu đơn không được lựa chọn thì có thể sử dụng mẫu đó cho kiểm tra lấy mẫu liên tiếp.
8.6. Lấy mẫu ngẫu nhiên không hoàn lại
Mẫu ngẫu nhiên đơn gồm n đơn vị riêng rẽ từ lô N đơn vị có thể được tạo ra không hoàn lại bằng một trong hai phương pháp dưới đây.
a) Phương pháp 1
1) Tạo số nguyên ngẫu nhiên K trong dải từ 1 đến và bao gồm cả N.
2) Xác nhận rằng giá trị K chưa được tạo ra trước đó; nếu nó khác biệt thì lưu lại giá trị đó còn nếu không thì loại ra.
3) Lặp lại bước 1) và bước 2) cho đến khi thu được n giá trị của K.
b) Phương pháp 2
1) Tạo hoán vị ngẫu nhiên N đơn vị, mỗi lần lấy n theo 8.3.
2) Sử dụng các giá trị n đầu tiên trong đầu ra dãy A làm mẫu ngẫu nhiên.
CHÚ THÍCH: Có thể sử dụng một trong hai phương pháp này để thu được số mẫu với cỡ mẫu bất kỳ (cho các mục đích như lấy mẫu hai lần hay lấy mẫu nhiều lần) bằng cách sử dụng tổng nt của cỡ mẫu riêng ni như giá trị đầu vào của n cho thuật toán này, để nguyên các giá trị ở thứ tự đầu ra ban đầu, sau đó lấy các giá trị kết quả n1 đầu tiên làm mẫu đầu tiên, các kết quả giá trị n2 tiếp theo làm mẫu thứ hai và cứ tiếp tục như vậy. Hơn nữa, nếu giá trị kết quả của một mẫu đơn không được chọn thì mẫu đó có thể được sử dụng cho kiểm tra lấy mẫu liên tiếp bằng cách kiểm tra từng đơn vị theo thứ tự được chọn.
8.7. Lấy mẫu ngẫu nhiên cho phương án lấy mẫu liên tục (CSP)
Phương án lấy mẫu liên tục CSP-1 được thiết kế để áp dụng cho việc kiểm tra chất lượng dây chuyền sản xuất và luân phiên giữa các giai đoạn kiểm tra 100% yêu cầu i đơn vị được chấp nhận liên tiếp trước khi tiến hành các giai đoạn tiếp theo của kiểm tra lấy mẫu ở xác suất f, với sự trở lại kiểm tra 100 % khi tìm thấy đơn vị không chấp nhận được. Trong các giai đoạn kiểm tra lấy mẫu, các đơn vị từ dây chuyền sản xuất có thể được chọn cho kiểm tra theo một trong hai phương pháp dưới đây.
a) Phương pháp 1
1) Đối với mỗi đơn vị sản xuất, tạo giá trị thực ngẫu nhiên U.
2) Nếu U nhỏ hơn hoặc bằng f thì chọn đơn vị đó cho kiểm tra lấy mẫu.
3) Lặp lại bước 1) và 2) cho đến khi thu được đơn vị không chấp nhận được.
b) Phương pháp 2
1) Đối với mỗi phân đoạn sản xuất n đơn vị, trong đó n bằng 1/f, tạo số nguyên ngẫu nhiên K trong dải từ 1 đến và bao gồm cả n.
2) Chọn đơn vị tương ứng với K làm đơn vị lấy mẫu để kiểm tra.
3) Lặp lại bước 1) và 2) cho đến khi thu được đơn vị không chấp nhận được.
CHÚ THÍCH: Đối với phương án CSP-1, giá trị f được quy định là nghịch đảo của số nguyên.
8.8. Lấy mẫu ngẫu nhiên phân tầng
Đối với lô gồm hai hay nhiều tầng cỡ N, chọn mẫu ngẫu nhiên đơn cỡ n, từ mỗi tầng i sử dụng các phương pháp nêu trong 8.3 hoặc 8.6 khi lấy mẫu không hoàn lại được yêu cầu hoặc phương pháp nêu trong 8.5 khi yêu cầu lấy mẫu có hoàn lại.
8.9. Lấy mẫu ngẫu nhiên một lần từ cỡ lô ban đầu chưa biết
Mẫu ngẫu nhiên đơn gồm n đơn vị khác nhau từ một lô ban đầu chưa biết cỡ lô, nhưng ít nhất là bằng cỡ n, có thể thu được theo phương pháp dưới đây (lấy từ tài liệu tham khảo[11]).
a) Ấn định các đơn vị n đầu tiên từ lô cho dãy mẫu A[1:n].
b) Nếu có đơn vị khác trong lô liệt kê thì đặt N bằng số đếm đơn vị tiếp theo; nếu không thì thực hiện bước f).
c) Tạo số nguyên ngẫu nhiên K trong dải từ 1 đến và bao gồm cả N.
d) Nếu K nhỏ hơn hoặc bằng n thì đặt A[K] bằng N.
e) Thực hiện bước b).
f) Thu được mẫu ngẫu nhiên từ dãy A và cỡ lô từ giá trị N.
CHÚ THÍCH: Phương pháp này cũng có thể sử dụng khi đã biết cỡ lô.
8.10. Lấy mẫu ngẫu nhiên một lần theo thứ tự, không hoàn lại
Mẫu ngẫu nhiên đơn gồm n đơn vị riêng biệt từ lô N đơn vị có thể được tạo ra trực tiếp theo thứ tự tăng dần theo các phương pháp dưới đây.
a) Phương pháp 1(lấy từ tài liệu tham khảo [2])
1) Khởi tạo các biến sau:
i) tạo dãy A[1:n];
ii) đặt L bằng N, K bằng N – n và J bằng 0.
2) Tăng J thêm 1.
3) Nếu J lớn hơn n thì đi tiếp bước 8).
4) Tạo giá trị thực ngẫu nhiên U và đặt P bằng 1.
5) Đặt P bằng P K / N.
6) Nếu P nhỏ hơn hoặc bằng U:
i) đặt A[J] bằng N – L +1 sau đó tăng L thêm 1;
ii) thực hiện bước 2).
7) Nếu P lớn hơn U:
i) tăng L thêm 1 và K thêm 1;
ii) thực hiện bước 5).
8) Thu được mẫu ngẫu nhiên theo thứ tự tăng dần từ dãy A.
b) Phương pháp 2 (lấy từ tài liệu tham khảo [3])
1) Lấy C(a,b) là hàm số thu được số tổ hợp các đơn vị lấy a lấy b mỗi lần (còn gọi là hệ số nhị thức và bằng a! / [(a-b)! b!]).
2) Tạo số nguyên ngẫu nhiên L trong dải từ 1 đến và bao gồm cả C(N,n).
3) Tạo dãy A[1:n].
4) Đặt K bằng 0, J bằng 1 và m bằng n – 1.
5) Đặt A[J] bằng 0.
6) Nếu J không bằng 1 thì đặt A[J] bằng A[J – 1].
7) Đặt A[J] bằng A[J] +1.
8) Đặt R bằng C(N - A[J], n – J).
9) Tăng K thêm R.
10) Nếu K nhỏ hơn L thì thực hiện bước 7).
11) Giảm K đi R.
12) Tăng J thêm 1.
13) Nếu J nhỏ hơn hoặc bằng N thì thực hiện bước 5).
14) Đặt A[n] bằng A[m] + L – K.
15) Thu được mẫu ngẫu nhiên theo thứ tự tăng dần từ dãy A
CHÚ THÍCH: Do những hạn chế trong trình bày lượng số nguyên lớn trên máy tính cũng như những giới hạn trong độ phân giải của bộ tạo số ngẫu nhiên, cần chú ý để đảm bảo rằng Phương pháp 2 có thể thực hiện được bằng máy tính và không có độ chệch quá mức do bộ tạo số ngẫu nhiên được sử dụng.
VÍ DỤ: Mẫu ngẫu nhiên gồm 5 đơn vị sắp xếp theo thứ tự được yêu cầu lấy từ lô gồm 25 đơn vị. Có thể tạo 25! / (20! 5!) = 53 130 tổ hợp gồm 5 đơn vị từ 25 đơn vị, thực hiện được trên máy tính hiện đại. Ngoài ra, bộ tạo số ngẫu nhiên mô tả ở Điều 7 được chọn cho mục đích lấy mẫu này; giá trị đầu ra tối đa của nó là 2 147 483 562 lớn hơn trên 40 419 lần so với dải yêu cầu nên độ chệch tạo ra trong phương pháp này là không đáng kể đối với mục đích thực tiễn. Số nguyên ngẫu nhiên đơn từ 1 đến và bao gồm cả 53 130 được tạo ra là 7 319. Tập hợp mẫu thu được là {1, 7, 13, 18, 19}.
8.11. Lấy mẫu chùm
Đối với tổng thể hoặc lô gồm chùm các đơn vị liên quan, ghi các chùm vào một danh mục và chọn ngẫu nhiên từ danh mục này sử dụng các phương pháp nêu trong 8.3 hoặc 8.6 khi lấy mẫu không hoàn lại được yêu cầu hoặc phương pháp nêu trong 8.5 khi yêu cầu lấy mẫu có hoàn lại. Mẫu thu được bao gồm tổng số đơn vị trong các chùm được chọn.
8.12. Lấy mẫu ngẫu nhiên với xác suất tỷ lệ thuận với cỡ mẫu
Đối với tổng thể gồm các đơn vị có tích hợp khác nhau, có thể thu được mẫu ngẫu nhiên các đơn vị được chọn tỷ lệ với cỡ mẫu bằng cách sử dụng một trong hai phương pháp dưới đây.
a) Phương pháp 1
1) Trong danh mục N đơn vị có cỡ khác nhau, ghi lại cỡ mẫu cộng dồn Si của các đơn vị bên cạnh từng đơn vị liên tiếp.
2) Tạo số nguyên ngẫu nhiên K trong dải từ 1 đến và kể cả SN, trong đó SN là cỡ cộng dồn của toàn bộ tổng thể.
3) Từ danh mục, chọn đơn vị kèm theo cỡ cộng dồn lớn nhất không vượt quá K làm thành phần mẫu.
4) Lặp lại bước 2) và 3) cho đến khi thu được số n đơn vị lấy mẫu (có hoàn lại hoặc không hoàn lại) mong muốn.
b) Phương pháp 2
1) Từ danh mục N đơn vị có cỡ khác nhau, xác định cỡ đơn vị lớn nhất M.
2) Tạo cặp số nguyên ngẫu nhiên (K, L) với K trong dải từ 1 đến và kể cả N và L trong dải từ 1 đến và kể cả M.
3) Nếu cỡ đơn vị K không vượt quá M thì chọn đơn vị K làm thành phần mẫu.
4) Lặp lại bước 2) và 3) cho đến khi thu được số n đơn vị lấy mẫu (có hoàn lại hoặc không hoàn lại) mong muốn.
VÍ DỤ: Một công ty marketing muốn tiến hành một cuộc khảo sát các hộ gia đình với lựa chọn tỷ lệ với cỡ hộ gia đình (nghĩa là số nhân khẩu). Thu được một danh sách 10 hộ gia đình xếp theo thứ tự số lượng nhân khẩu (cỡ mẫu) và các cỡ là {2, 2, 3, 3, 3, 4, 4, 5, 6, 7}. Cỡ cộng dồn của danh sách này là: {2, 4, 7, 10, 13, 17, 21, 26, 32, 39}. Mẫu ngẫu nhiên không hoàn lại gồm 4 hộ gia đình được yêu cầu. Số nguyên ngẫu nhiên từ 1 đến và kể cả 39 được tạo ra, thu được {7, 33, 2, 11}. Đơn vị lấy mẫu tương ứng là các hộ gia đình với thứ hạng liệt kê: {3, 10, 1, 5}.
8.13. Lấy mẫu nhiều tầng
Đối với tổng thể hoặc lô có cấu trúc lồng nhóm thứ bậc nhỏ dần, chọn mẫu ngẫu nhiên từ các nhóm lớn nhất, sau đó các nhóm con nhỏ hơn từ mỗi nhóm được chọn trước đó, tiếp tục quy trình này cho đến khi đạt đến từng cấp đơn vị trong hồ sơ. Ở mỗi tầng, sử dụng phương pháp lấy mẫu ngẫu nhiên nêu trong 8.3 hoặc 8.6 khi lấy mẫu không hoàn lại được yêu cầu hoặc phương pháp nêu trong 8.5 khi yêu cầu lấy mẫu có hoàn lại. Số đơn vị trong mẫu là tích của số mẫu được lấy ở mỗi tầng.
VÍ DỤ: Một lô gồm 20 palet, mỗi palet có 20 thùng. Mỗi thùng có 10 đơn vị. Người mua muốn kiểm tra sản phẩm bằng phương án lấy mẫu nhiều tầng. Một mẫu ngẫu nhiên gồm 4 palet được chọn. Sau đó, từ mỗi palet được chọn, chọn ra mẫu ngẫu nhiên gồm 4 thùng. Cuối cùng, từ mỗi thùng được chọn, chọn ra mẫu ngẫu nhiên gồm 3 đơn vị. Quy trình này thu được một mẫu gồm 48 đơn vị từ 4 000 đơn vị trong lô.
8.14. Ngẫu nhiên hóa trong thiết kế thực nghiệm
Trong các ứng dụng thiết kế thực nghiệm, ngẫu nhiên hóa được sử dụng để thực hiện những hoạt động như phân bổ các xử lý thực nghiệm cho các đơn vị hoặc đối tượng và thiết lập thứ tự đánh giá các đơn vị, bao gồm cả thứ tự đánh giá đối với các thiết kế lặp. Có thể sử dụng một trong hai phương pháp ngẫu nhiên hóa dưới đây.
a) Phương pháp 1
1) Ẩn định số nguyên từ 1 đến N cho từng phần tử trong danh mục N xử lý hoặc đơn vị, tùy trường hợp.
2) Tạo hoán vị ngẫu nhiên N số nguyên được lấy (nghĩa là tất cả) tại một thời điểm.
3) Tiến hành hoạt động thực nghiệm theo trình tự thu được từ bước 2).
b) Phương pháp 2
1) Tạo N biến thực ngẫu nhiên Ui và ấn định từng giá trị theo thứ tự tạo ra cho từng phần tử liên tiếp trong danh mục các xử lý hoặc đơn vị, tùy trường hợp.
2) Sắp xếp danh mục xử lý hoặc đơn vị theo thứ tự tăng dần theo giá trị tương ứng U của chúng.
3) Tiến hành hoạt động thực nghiệm theo trình tự thu được từ bước 2).
VÍ DỤ 1: Nhà nghiên cứu y học muốn thử nghiệm tác dụng của một loại thuốc mới so với điều trị sử dụng thông thường trong điều kiện y tế đặc biệt. Mười hai đối tượng tình nguyện và được đánh số từ 1 đến 12 khi tham gia vào thử nghiệm lâm sàng này. Nhà nghiên cứu hoạch định phân bổ điều trị A (thuốc mới) cho 6 đối tượng và điều trị B (thuốc hiện thời) cho sáu đối tượng còn lại. Như một công đoạn làm giảm độ chệch, trước hết thử nghiệm viên quyết định ngẫu nhiên hóa thứ tự 12 điều trị trước khi phân bổ chúng vào danh mục ngẫu nhiên hóa 12 đối tượng. Từng số chỉ số các điều trị và đối tượng được ngẫu nhiên hóa riêng theo phương pháp 1. Danh mục ngẫu nhiên hóa thu được của các điều trị là {B, B, A, B, A, A, B, B, A} và danh mục ngẫu nhiên hóa đối tượng là {3, 7, 12, 5, 1, 9, 11, 4, 10, 2, 8, 6}. Lúc này các điều trị có thể phân bổ trực tiếp cho các đối tượng dựa trên thứ tự trong các danh mục, thu được {B3, B7, A12, B5, A1, A9, B11, A4, A10, B2, B8, B6}. Kết quả là điều trị A được phân bổ cho các đối tượng {1, 4, 6, 9, 10, 12} còn điều trị B được phân bổ cho các đối tượng {2, 3, 5, 7, 8, 11}.
VÍ DỤ 2: Người thử nghiệm muốn tiến hành thực nghiệm lặp lại, thử nghiệm từng đơn vị trong số 5 đơn vị theo thứ tự ngẫu nhiên tại ba thời điểm khác nhau. Tập hợp {1, 2, 3, 4, 5} được hoán vị ngẫu nhiên theo phương pháp 1, thu được ba danh mục theo thứ tự như sau: {2, 1, 5, 4, 3}, {1, 5, 2, 3, 4}, {4, 3, 5, 2, 1}. Ba danh mục này được ấn định theo thứ tự lần thử tương ứng là 1, 2 và 3 và thử nghiệm viên thử nghiệm các đơn vị theo thứ tự quy định trong danh mục kèm theo từng lần thử.
8.15. Hình vuông La tinh ngẫu nhiên
Hình vuông La tinh ngẫu nhiên bậc n là dãy n x n chứa các ký hiệu từ bảng chữ cái cỡ n, sắp xếp sao cho mỗi ký hiệu xuất hiện đúng một lần trong mỗi hàng và đúng một lần trong mỗi cột. Sẽ hữu ích trong việc hoạch định một số loại hoạch định một số loại thiết kế thực nghiệm. Hình vuông La tinh ngẫu nhiên bậc n có thể tạo ra bằng phương pháp dưới đây (từ tài liệu tham khảo [4]).
a) Tạo dãy A[1:n, 1:n] và C[1:n].
b) Đặt R bằng 1.
c) Ấn định các số nguyên từ 1 đến n cho dãy C[1:n]
d) Đặt J bằng N.
e) Đặt C bằng 1.
f) Đặt I bằng 0.
g) Tạo số nguyên ngẫu nhiên X trong dải từ 1 đến và bao gồm cả J.
h) Đặt H bằng 1.
i) Nếu I lớn hơn 50, thực hiện bước c).
j) Nếu A[H, C] bằng C[X] tăng I thêm 1 và thực hiện bước g).
k) Tăng H thêm 1.
l) Nếu H lớn hơn hoặc bằng R – 1, thực hiện bước i).
m) Đặt A[R, C] bằng C[X], giảm J đi 1
n) Nếu X lớn hơn J, thực hiện bước r).
o) Đặt K bằng X.
p) Đặt C[K] bằng C[K+1].
q) Tăng K thêm 1; nếu K nhỏ hơn hoặc bằng J, thực hiện bước p).
r) Tăng C thêm 1; nếu C nhỏ hơn hoặc bằng n, thực hiện bước f).
s) Tăng R thêm 1; nếu R nhỏ hơn hoặc bằng n, thực hiện bước c).
t) Thu được hình vuông La tinh ngẫu nhiên từ dãy A.
CHÚ THÍCH: Thuật toán tạo các hình vuông La tinh ngẫu nhiên phân bố đều có thể thấy trong tài liệu tham khảo [5]. Ngoài ra, cần chú ý rằng có sự kết nối giữa hình vuông La tinh ngẫu nhiên và việc tạo ra xáo trộn ngẫu nhiên một hoán vị vì mỗi hàng và cột hình vuông La tinh là một xáo trộn của tất cả các hàng và các cột trước đó.
(quy định)
A.1. Mô tả
Phụ lục này đưa ra hai bảng số ngẫu nhiên áp dụng khi không có sẵn máy tính để thực hiện các thuật toán tạo số ngẫu nhiên của tiêu chuẩn này. Mỗi bảng gồm 3 600 số ngẫu nhiên từ 0 đến 9, mỗi số xuất hiện với tần suất bằng nhau. Các bảng đều được sắp xếp dưới dạng 60 hàng và 60 cột để thuận tiện cho việc sử dụng thời gian trong ngày làm điểm khởi đầu. Các bảng được tạo ra bằng cách sử dụng các thuật toán mô tả trong Điều 7.
A.2. Sử dụng
A.2.1. Số chữ và giải thích
A.2.1.1. Xác định số chữ m cần thiết để thể hiện cỡ lô N. Số chữ số bằng số chữ số trong cỡ lô trừ trường hợp cỡ lô là lũy thừa của 10; trong trường hợp này, bỏ qua số đầu trong cỡ lô và giải thích các số không còn lại là số chữ số yêu cầu cũng như bằng với giá trị cỡ lô (ví dụ nếu N = 100, giải thích giá trị 00 là 100).
A.2.1.2. Khi cỡ lô nhỏ hơn hoặc bằng một nửa của 10m thì các số nhập vào bảng có thể được giải thích dựa trên ánh xạ của giá trị quan trắc lên dải từ 1 đến N, với điều kiện là độ chệch không được đưa vào quá trình này. Điều này có thể được thực hiện bằng cách bỏ qua tất cả các giá trị vượt quá kN, trong đó k = ë10m / Nû, trước khi ánh xạ giá trị theo công thức v2 = 1 + (v1 – 1) mô đun N, trong đó v1 là giá trị ban đầu và v2 là giá trị ánh xạ vào dải mong muốn.
A.2.2. Điểm bắt đầu
A.2.2.1. Trước khi có thể thu được các số trong bảng, cần quyết định về kế hoạch chọn điểm bắt đầu. Các bảng được thiết kế để dễ dàng cho phép thời gian trong ngày từ đồng hồ có thể hiển thị thời gian tính đến giây sử dụng cho mục đích này. Dưới đây là phương pháp có thể sử dụng.
a) Ghi thời gian hiện tại dưới dạng “giờ:phút:giây”.
b) Sử dụng giá trị giây để xác định giá trị hàng, giải thích 00 là 60.
c) Sử dụng giá trị phút để xác định giá trị cột, giải thích 00 là 60.
d) Sử dụng giá trị giờ để xác định việc sử dụng Bảng A.1 hay Bảng A.2, dựa trên giá trị là chẵn hay lẻ.
VÍ DỤ: Thử nghiệm viên mong muốn chọn điểm bắt đầu trong bảng để chọn mẫu ngẫu nhiên từ lô gồm 100 đơn vị. Thời gian hiện thời được ghi là 10:35:23. Do đó, tọa độ nhập vào bảng là hàng 13 cột 53 của Bảng A.2 (vì 10 là số chẵn). Chữ số tại vị trí đó là 6 nhưng vì cần hai chữ số để chọn mẫu từ 100 đơn vị nên giá trị từ cột 36 cũng được tính để nhận biết đơn vị mẫu đầu tiên là 66.
A.2.2.2. Cũng có thể sử dụng phương pháp bất kỳ khác đưa ra nguồn ngẫu nhiên các số nguyên phân bố đều tong phạm vi dải từ 1 đến và bao gồm cả 60 như phương pháp đồng xu hay xúc sắc trong 5.2 hoặc thuật toán trên máy tính trong Điều 7 (có thể sử dụng để tạo một danh mục dài các tọa độ ngẫu nhiên để sử dụng vào những lần liên tiếp). Ngoài ra, khi kết thúc việc chọn mẫu từ bảng trong một lần cụ thể, có thể ghi lại các tọa độ nhập ngay tiếp sau và sau đó sử dụng làm điểm bắt đầu cho lần lấy mẫu tiếp theo.
VÍ DỤ: Tiếp tục với ví dụ ở A.2.2.1, giả định rằng mẫu ngẫu nhiên có hoàn lại gồm 10 đơn vị được yêu cầu và hướng được sử dụng để chọn những số này là hướng đi xuống. Mẫu thu được là {66, 13, 10, 45, 32, 22, 41, 49, 22, 99}. Tọa độ của giá trị ngay sau đó là hàng 23 và cột 35. Các giá trị này có thể được ghi lại và sử dụng làm điểm nhập khi mẫu được yêu cầu cho lần tiếp theo.
A.2.2.3. Tọa độ nhập cũng có thể được xác định bằng cách thiết lập chữ số ban đầu dựa trên các giá trị hàng và cột từ A.2.2.1 hoặc A.2.2.2, và các chữ số bổ sung dựa trên giá trị của hàng hiện thời và cột bổ sung dựa trên các số được tạo ngẫu nhiên không hoàn lại trong dải từ 1 đến và kể cả 60 đối với các chữ số m – 1 còn lại yêu cầu. Số nhiều chữ số thu được hình thành theo thứ tự các số nhập trong cột được tạo ra.
VÍ DỤ: Một mẫu ngẫu nhiên từ lô 1 000 được yêu cầu. Hàng và cột đầu tiên được xác định tương ứng là 5 và 11, trong Bảng A.1. Cần thêm hai chữ số nữa và chúng được tạo ra bên ngoài là 1 và 30, thu được tọa độ sau đây tương ứng cho chữ số đầu tiên, thứ hai và thứ 3: (5, 11), (5, 1) và (5, 30). Hướng lấy trong bảng được quyết định là hướng đi xuống. Do đó, số đầu tiên là 511, tiếp theo là 943, 419, 413, 899, 209, …
A.2.3. Xử lý với các ranh giới của bảng
A.2.3.1. Khi đọc số gồm m chữ số và các chữ số phía bên phải của chữ số đầu tiên vượt quá cột thứ 60 thì coi các cột 1, 2, … tương ứng là cột 61, 62, … Có thể áp dụng nguyên tắc này trong phạm vi bảng hiện hành hoặc bằng cách coi bảng số ngẫu nhiên khác là mở rộng của bảng đầu tiên.
A.2.3.2. Nguyên tắc thông thường là thu được các số ngẫu nhiên tiếp theo bằng cách tăng giá trị hàng thêm một và đọc m chữ số của số đó dựa trên các giá trị cột xác định trước và thứ tự của chúng. Khi giá trị của hàng này vượt quá hàng thứ 60 thì coi hàng 1 là hàng 61 và tăng giá trị cột thêm m trong trường hợp các cột được sử dụng liên tiếp hoặc tăng thêm một trong trường hợp A.2.2.3 được sử dụng để thiết lập các cột, và tiếp tục thu được các số. Có thể áp dụng nguyên tắc này trong phạm vi bảng hiện hành hoặc bằng cách coi bảng số ngẫu nhiên khác là mở rộng của bảng đầu tiên, với điều kiện là nó chưa được sử dụng như theo A.2.3.1.
A.2.4. Hồ sơ đánh giá
Khi hồ sơ được yêu cầu lưu giữ cho mục đích đánh giá bởi cơ quan chịu trách nhiệm hoặc cơ quan chức năng, thì ghi lại cỡ lô và cỡ mẫu.
Ngoài ra, đối với các bảng và sử dụng bảng, ghi lại
a) hàng ban đầu,
b) (các) cột ban đầu và thứ tự của chúng,
c) hướng lấy trong bảng,
d) bảng ban đầu sử dụng và cách thức mở rộng bởi bảng khác, nếu áp dụng, và
e) ánh xạ sử dụng.
Bảng A.1 – Số ngẫu nhiên (đối với giá trị lẻ)
| Hàng i | Cột j. | |||||||||||
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | |
|
5 | 95183 08509 45448 02230 13275 | 14683 97009 66819 00022 96798 | 96585 47525 86936 46390 51425 | 84761 88791 95349 76658 67147 | 65044 93751 08657 91934 15216 | 65183 70490 75106 64676 71831 | 55567 17749 97487 42429 16229 | 28734 32927 85268 96812 25862 | 19802 65080 59208 30560 22090 | 56410 94970 43206 99913 91420 | 79127 55541 14898 72809 24352 | 02879 89466 29083 66736 03550 |
|
10 | 44439 17629 14328 96896 09725 | 33385 80967 77127 02466 80938 | 95151 42144 40397 86706 27971 | 92374 58190 78105 09507 01243 | 14683 24550 75031 66840 29232 | 00323 62189 99553 68509 28799 | 57667 94525 84296 38033 88456 | 78341 44967 01482 90785 99618 | 09004 15860 25738 75831 20071 | 80139 85739 32761 98886 79865 | 81132 93323 85035 00905 63584 | 87552 87043 68873 48343 69087 |
|
15 | 55021 06492 20604 20202 27160 | 37184 95014 54145 58870 01595 | 69480 54908 27781 67569 64831 | 56317 21591 35157 71756 07126 | 19944 13771 50127 76284 25821 | 56756 35967 61025 30909 81524 | 37514 78637 57344 87763 12585 | 86439 29918 36615 21951 76273 | 69831 47923 07766 67756 36256 | 15172 61404 83959 82597 41879 | 81398 63378 34546 15210 33287 | 69574 72394 67011 04291 84361 |
|
20 | 95089 74825 80338 16596 34134 | 78572 21529 94074 43179 42056 | 87167 24660 65731 42026 40153 | 65888 33314 39470 94264 00994 | 93358 64512 03807 28301 14179 | 23879 80550 72355 29514 44447 | 84496 51712 40407 60657 99399 | 16147 23057 86049 21732 86963 | 31130 53841 81583 21548 71862 | 96978 32470 06786 28693 01306 | 80361 36790 16673 15241 15489 | 85195 60455 06017 68944 00515 |
|
25 | 01118 67371 03485 33328 84302 | 98623 71659 55173 74045 10060 | 33695 30505 68477 25331 25334 | 49221 71239 12348 37635 84920 | 97197 56944 76971 39081 30270 | 21424 35898 64800 28786 09722 | 91691 02207 86498 20843 61706 | 09365 93274 42059 32565 52863 | 62483 40142 08942 24316 03417 | 98893 98319 32931 17888 95658 | 22106 41218 73896 47626 74490 | 45399 43739 27772 69199 00143 |
|
30 | 94775 51700 75920 32385 13424 | 52191 63604 13260 28423 00587 | 94552 96771 44283 46784 12231 | 99265 34444 27735 59222 44543 | 55079 30002 31134 17776 62984 | 64517 67975 97100 57726 58391 | 16803 93167 36706 56449 22054 | 13037 16746 24404 32109 16134 | 50984 97842 56970 11825 73790 | 14886 25589 44575 57995 59050 | 04385 12568 68832 91217 24893 | 67907 81785 42374 12802 62342 |
|
35 | 90896 60682 38746 51658 49174 | 00608 38700 34667 18422 12449 | 31377 34039 84499 05732 97583 | 53338 93512 70915 91001 85835 | 84813 38596 91391 98070 82313 | 76825 40004 25660 13591 96349 | 92192 71447 12328 44468 92721 | 24937 97193 35273 88460 64617 | 81481 52407 08135 66964 06030 | 01866 44146 04799 24038 22312 | 22641 77116 14489 93987 94263 | 21817 99965 19984 66335 80291 |
|
40 | 44215 33877 83411 27135 29475 | 21953 94654 43288 82404 31431 | 21844 10025 47832 52031 46863 | 44114 84935 40488 44648 70098 | 93162 94630 89085 97600 98659 | 51028 49660 69731 72166 72035 | 29551 23473 00790 70830 21538 | 66121 89644 60182 27701 12923 | 63959 67212 71358 01755 76963 | 97789 75851 22571 00523 78288 | 44259 83767 94204 01837 59083 | 90865 45647 64211 31304 18839 |
|
45 | 56886 55061 01646 41789 26066 | 38711 35916 62126 28167 80119 | 66126 15955 37253 90577 44259 | 16504 28228 24997 84499 94514 | 87900 36994 53016 25059 21211 | 74055 73167 96515 90583 44302 | 46028 17137 40536 09422 29023 | 84821 36572 39311 87357 28138 | 83323 48592 64151 55416 03693 | 35962 60721 93960 81135 50650 | 27522 97714 24053 41286 38450 | 87875 61215 87645 92320 61118 |
|
50 | 63559 35054 32826 07860 79276 | 20927 84077 26937 90064 72512 | 12881 02504 75563 91220 19525 | 25582 10800 14290 46786 27397 | 07872 75293 30078 45994 88975 | 28073 86466 70820 47375 77137 | 59006 92406 58639 70140 40032 | 55666 56289 64900 35592 06205 | 68690 79081 61699 05990 06997 | 59772 55271 34974 58470 53504 | 25162 73177 11738 82014 07760 | 87924 70568 64065 05265 62546 |
|
55 | 41093 27382 38924 51411 80310 | 04332 27938 47230 44221 18848 | 68677 91695 59448 93363 23722 | 27073 64013 97802 48654 30788 | 94104 46719 37987 42656 27435 | 58532 61629 22733 99464 03780 | 53616 33668 52199 08481 85737 | 32156 32391 12325 98128 05561 | 66153 35411 18625 66677 57203 | 00264 68209 01271 89441 07316 | 36374 33885 84870 66019 98597 | 15230 64050 10911 75095 73621 |
|
60 | 40082 86922 07932 20383 45471 | 39571 84354 69932 07288 31340 | 89790 81939 18796 50265 30187 | 65382 32180 87070 48321 23899 | 01447 32891 82202 63056 36361 | 15984 52704 05372 35861 96780 | 60854 84659 93506 80864 55823 | 72833 95442 60697 86357 37743 | 87320 86204 48535 51567 06957 | 95245 44040 89027 68151 77884 | 40678 51613 45719 11723 78061 | 89785 15984 51567 06990 36603 |
Bảng A.2 – Số ngẫu nhiên (đối với giá trị chẵn)
| Hàng i | Cột j | |||||||||||
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | |
|
5 | 51326 96821 67104 93315 45823 | 91644 43647 67934 93110 44862 | 88971 41707 95662 01022 86472 | 00664 91062 85259 16079 77354 | 10776 20037 08546 74364 95916 | 90888 47660 77032 97582 36599 | 97107 34652 28958 34309 52350 | 00930 82087 26815 18699 89866 | 87438 29652 66683 24437 98532 | 23714 51614 50539 12839 69704 | 33246 11015 65189 48005 33735 | 72109 66187 22993 46478 13696 |
|
10 | 32573 74553 06794 75606 97535 | 58513 41700 48960 34848 55169 | 70797 25357 75160 74458 47044 | 53560 17428 18552 71100 81940 | 23115 66708 00424 01512 16507 | 38325 83630 25976 89662 12220 | 74380 42360 69852 01391 16375 | 99917 16842 35837 49140 65306 | 21721 40782 69810 18048 38691 | 00323 21345 64014 59282 75019 | 29402 88668 03045 77344 55186 | 27080 95845 53378 72419 47269 |
|
15 | 89809 88095 48854 97951 48953 | 48811 48475 75803 73015 47945 | 09494 07399 34089 36585 81153 | 06576 02165 45335 89007 10121 | 58258 98038 13056 12069 69935 | 73115 97247 44509 96858 60894 | 46712 48441 77886 17241 23151 | 11106 93066 65036 37189 00113 | 38382 20276 42619 44193 40597 | 70893 72169 95564 28270 71164 | 39503 49706 66315 81624 61331 | 42937 56553 49084 75256 10930 |
|
20 | 83334 31105 94245 19221 33503 | 44992 74546 19396 70541 45776 | 30210 74875 03648 58195 88514 | 99370 51747 28548 21383 10094 | 60425 41021 42987 57877 28589 | 87391 22338 78668 27812 47548 | 63244 49403 09292 06504 64714 | 54828 20173 23073 18289 96174 | 12155 75454 21116 18606 10026 | 64082 62122 07199 17860 87111 | 43773 37227 21398 09218 29333 | 66172 35790 18770 58984 77885 |
|
25 | 03602 43277 31966 19193 98935 | 99374 65791 42142 31952 48606 | 41918 12217 71410 87947 27475 | 43875 23767 28139 89521 73462 | 11258 09833 60147 65225 66692 | 83646 66504 68496 97987 11151 | 46042 82359 89021 14794 21709 | 26986 95754 01615 90695 32836 | 11003 40249 36565 69314 92997 | 94756 71472 85598 10359 33682 | 89972 61588 18048 27881 12722 | 00805 04428 32584 38183 38906 |
|
30
35 | 21880 81695 68883 59547 91709 57195 03657 93373 35158 38056 | 10506 06183 60266 60741 73154 97283 71909 88795 50868 14298 | 78478 08147 66180 56065 86898 25156 82018 11353 45055 10431 | 85067 01241 05680 71467 20234 59277 83110 44726 12180 53147 | 30375 16278 38799 07193 05773 33608 21722 66989 29993 76843 | 82944 54886 40481 38784 47157 73937 03455 24389 69555 32128 | 06660 36468 73524 08169 72305 19341 30654 93445 69613 46844 | 40750 21315 73255 07389 20819 17262 57890 53752 69358 23407 | 84252 49106 79950 64049 57301 63955 18530 98703 96861 62423 | 20463 10291 42007 21355 89018 41678 60458 55276 01667 01712 | 37184 16837 56334 86589 74851 36229 57145 18391 47738 46033 | 27248 40481 54332 06583 50560 54204 08764 53513 11964 64425 |
|
40 | 49152 80000 53597 09151 99734 | 05010 90734 22379 34061 68144 | 84942 70131 94302 64751 63963 | 25483 19986 15425 96631 73011 | 52825 34949 62185 50373 22832 | 17485 76990 27894 61603 98145 | 67614 48325 37281 84917 31523 | 12493 39323 38876 56084 60195 | 88626 66921 97902 57647 34172 | 39589 89134 34008 80898 40637 | 56044 21853 45051 55489 60940 | 21968 18973 05607 24602 51237 |
|
45 | 84547 18815 14169 90528 99055 | 89655 26665 38336 60501 42696 | 53120 25301 41192 73201 14376 | 95599 67754 56208 72999 24907 | 04602 88457 29069 30335 06082 | 07968 19913 87045 86428 61789 | 85748 96787 32135 39401 03963 | 74914 71084 25975 72077 64664 | 76227 14867 71643 48056 09132 | 07158 03077 74200 17853 87218 | 24432 89575 52556 24894 64755 | 22963 66834 30213 19838 46107 |
|
50 | 62530 74196 27293 94220 68430 | 10183 77214 56047 93209 23169 | 38149 89483 73998 32369 58879 | 70004 43933 19996 82003 97812 | 74983 80953 94427 82433 39399 | 02092 81268 09157 85790 71469 | 40704 46485 62999 47632 40835 | 01062 23647 88803 36285 04924 | 17000 98173 81272 68771 30336 | 61170 55947 22315 06006 59222 | 99026 96727 92708 37556 06350 | 24025 86378 07343 51601 45656 |
|
55 | 61949 57248 10777 06717 09519 | 23031 90383 53979 92287 67689 | 50698 23502 65288 42775 13829 | 85772 22642 39116 79274 30992 | 85990 80722 80635 90874 44921 | 36942 38164 49653 44006 67375 | 11098 12160 36903 27312 94754 | 06636 51707 33854 15909 95322 | 57547 22075 79873 25276 25501 | 73247 20624 67823 59863 78486 | 46229 91644 23256 75607 99059 | 52551 08780 31643 22277 62524 |
|
60 | 57335 14911 04837 14430 68896 | 48704 08271 08929 20139 64599 | 79426 21662 81607 15027 91227 | 49770 40886 33210 52208 55882 | 32989 53783 61894 16440 60220 | 22640 76430 17240 59911 70202 | 88230 41233 37617 57566 73354 | 66598 44057 56753 22227 34776 | 27685 28385 61251 60109 55530 | 29719 21751 49433 95260 20599 | 99930 51746 65644 21388 45720 | 26181 64387 63758 96686 75145 |
(tham khảo)
MÃ MÁY TÍNH THUẬT TOÁN TẠO SỐ NGẪU NHIÊN
B.1. Tổng quan
Bộ mã dưới đây được viết trên ngôn ngữ lập trình C (xem tài liệu tham khảo [6] về chi tiết ngôn ngữ và đưa ra việc áp dụng các thuật toán mô tả ở Điều 7. Tài liệu tham khảo cho các phần liên quan của Điều 7 được nêu trực tiếp trong phần ghi chú trong các phân đoạn mã lập trình để hỗ trợ việc chuyển dịch sang các ngôn ngữ lập trình khác.
B.2. Chương trình minh họa

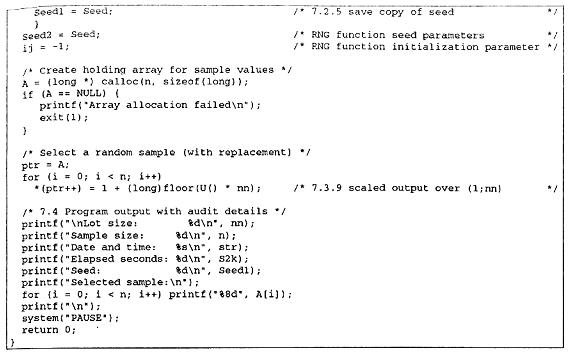
B.3. Hàm tạo giá trị xuất phát ngẫu nhiên tự động
Khi giá trị xuất phát nhập bằng tay được yêu cầu cho mục đích xác nhận hay đánh giá như đề cập ở 7.1.3 thì không gọi hàm này.
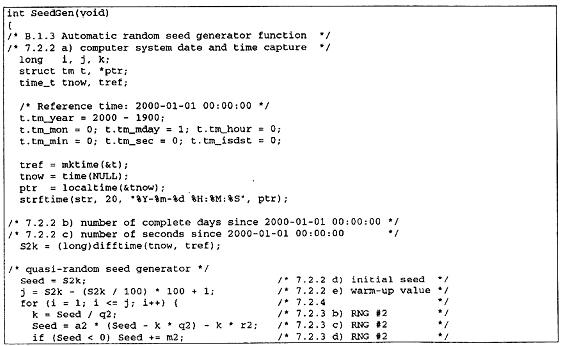

B.4. Hàm tạo số ngẫu nhiên
Khi tùy chọn giá trị xuất phát nhập bằng tay theo 7.1.3 thì tham số “giá trị xuất phát” (và do đó “Seed2”) được đặt bằng giá trị nhập bằng tay trước khi gọi hàm này.

(tham khảo)
LẤY MẪU NGẪU NHIÊN VÀ MÃ MÁY TÍNH NGẪU NHIÊN HÓA
C.1. Giới thiệu
Phụ lục này cung cấp ứng dụng ngôn ngữ lập trình C (xem tài liệu tham khảo [6] và chi tiết ngôn ngữ) cho các thuật toán lựa chọn mô tả ở Điều 8. Mã chương trình của Phụ lục này được viết để minh họa các mô tả trong Điều 8 và không phải là tùy chọn nhất thiết trong cấu trúc của nó.
C.2. Chương trình minh họa



C.3. Các hàm




[1] BAYS, C. and DURHAM, S.D. Improving a Poor Random Number Generator. ACM Transactions on Mathematical Software, 2 (1), 1976, pp. 59-64 (Cải tiến bộ tạo số ngẫu nhiên kém. Giao dịch ACM trên phần mềm toán học)
[2] BISSEL, A.F. Ordered random selection without replacement. Applied Statistics, 35, 1986, pp. 73-75 (Chọn ngẫu nhiên theo thứ tự, không hoàn lại. Thống kê ứng dụng)
[3] BUCKLES, B.P. and LYBANON, M. Algorithm 515, Generation of a Vector from the Lexicographical Index. ACM Transactions on Mathematical Software, 3 (2), 1977, pp. 180-182 (Tạo véctơ từ chỉ mục từ điển. Giao dịch ACM trên phần mềm toán học)
[4] BYERS, J.A. Random selection algorithms for spatial and temporal sampling. Computers in Biology and Medicine, 26, 1996, pp. 41-52 (Thuật toán chọn lọc ngẫu nhiên dùng cho lấy mẫu theo không gian và thời gian. Máy tính trong sinh học và y học).
[5] JACOBSON, M.T and MATTHEWS, P. Generating uniformly distributed random Latin squares. Journal of Combinatorial Design, 4, 1996, pp. 405-437 (Tạo hình vuông La tinh ngẫu nhiên phân bố đều. Tạp chí thiết kế tổ hợp)
[6] ISO/IEC 9899:1999, Programming languages – C (Ngôn ngữ lập trình C)
[7] L’ECUYER, P. An Efficient and Portable Combined Random Number Generator. Communications of the ACM, 31 (6), 1988, pp. 742-749, 774 (Bộ tạo số ngẫu nhiên kết hợp hiệu quả và di động. Truyền thông ACM)
[8] MARSAGLIA, G. Random Number Generators, Journal of modern Applied Statistical Methods, 2 (1), 2003, pp. 2-13 (Bộ tạo số ngẫu nhiên, Tạp chí phương pháp thống kê ứng dụng hiện đại)
[9] MCCULLOUGH, B.D. Assessing the Reliability of Statistical Software: Part II. The American Statistician, Vol. 53, No. 2 (May), 1999, pp. 149-159 (Đánh giá độ tin cậy của phần mềm thống kê: Phần II. Nhà thống kê học người Mỹ)
[10] MCCULLOUGH, B.D. and WILSON, B. On the Accuracy of Statistical Procedures in Microsoft EXCAL 97. Computational Statistics and Data Analysis, 31 (1), 1999, pp. 27-37 (Độ chính xác của quy trình thống kê trong Microsoft EXCEL 97. Thống kê và phân tích dữ liệu trên máy tính)
[11] MCLEOD, A.I and BELLHOUSE, D.R. A convenient algorithm for drawing a simple random sample. Applied Statistics, 32, 1983, pp. 182-184 (Thuật toán thuận lợi cho việc vẽ biến ngẫu nhiên đơn giản. Thống kê ứng dụng)
[12] PARK, S.K. and MILLER, K.W. Random Number Generators: Good Ones are Hard to Find. Communications of the ACM, 31 (10), 1988, pp. 1192-1201 (Bộ tạo số ngẫu nhiên: Khó tìm được sản phẩm tốt. Truyền thông ACM)
[13] PRESS, W.H., Teukolsky, S.A., Vetterling, W.T., and Flannery, B.P. Numerical Recipes in Fortran 77: The Art of Scientific Computing, Second Edition (volume 1 of Fortran Numerical Recipes), Cambridge University Press, Cambridge, UK, 1992, 2001 (Bí quyết số trong Fortran 77: Công nghệ Khoa học máy tính)
[14] SOM, R.K. A Manual of Sampling Techniques. Heinemann Educational Books Ltd., London 1973 (Sổ tay kỹ thuật lấy mẫu)
MỤC LỤC
Lời nói đầu
Lời giới thiệu
1. Phạm vi áp dụng
2. Tài liệu viện dẫn
3. Thuật ngữ, định nghĩa và ký hiệu
3.1. Thuật ngữ và định nghĩa
3.2. Ký hiệu
4. Quy định chung
5. Lấy mẫu ngẫu nhiên – Phương pháp dùng thiết bị cơ
5.1. Phương pháp bình
5.2. Phương pháp đồng xu hay xúc sắc
6. Lấy mẫu ngẫu nhiên giả độc lập – Phương pháp bảng số
6.1. Bảng số ngẫu nhiên
6.2. Phương pháp cơ bản
7. Lấy mẫu ngẫu nhiên giả độc lập – Phương pháp máy tính
7.1. Tổng quan
7.2. Thuật toán khởi tạo
7.3. Thuật toán tạo số ngẫu nhiên
7.4. Hồ sơ đánh giá
8. Áp dụng cho tình huống lấy mẫu phổ biến
8.1. Khái quát
8.2. Số nguyên ngẫu nhiên trong dải
8.3. Hóan vị ngẫu nhiên
8.4. Trộn ngẫu nhiên
8.5. Lấy mẫu ngẫu nhiên có hoàn lại
8.6. Lấy mẫu ngẫu nhiên không hoàn lại
8.7. Lấy mẫu ngẫu nhiên cho phương án lấy mẫu liên tục (CSP)
8.8. Lấy mẫu ngẫu nhiên phân tầng
8.9. Lấy mẫu ngẫu nhiên một lần từ cỡ lô ban đầu chưa biết
8.10. Lấy mẫu ngẫu nhiên một lần theo thứ tự, không hoàn lại
8.11. Lấy mẫu chùm
8.12. Lấy mẫu ngẫu nhiên với xác suất tỷ lệ thuận với cỡ mẫu
8.13. Lấy mẫu nhiều tầng
8.14. Ngẫu nhiên hóa trong thiết kế thực nghiệm
8.15. Hình vuông La Tinh ngẫu nhiên
Phụ lục A (quy định), Bảng số ngẫu nhiên
Phụ lục A (tham khảo), Mã máy tính thuật toán tạo số ngẫu nhiên
Phụ lục A (tham khảo), Lấy mẫu ngẫu nhiên và mã máy tính ngẫu nhiên hóa
Thư mục tài liệu tham khảo

