- 1 Tiêu chuẩn Việt Nam TCVN ISO 9000:2007 (ISO 9000 : 2005) về hệ thống quản lý chất lượng - cơ sở và từ vựng do Bộ Khoa học và Công nghệ ban hành
- 2 Tiêu chuẩn quốc gia TCVN 8244-1:2010 (ISO 3534-1:2006) về Thống kê học - Từ vựng - Phần 1: Thuật ngữ chung về thống kê và thuật ngữ dùng trong xác suất
- 3 Tiêu chuẩn quốc gia TCVN 8244-2:2010 (ISO 3534-2:2006) về Thống kê học - Từ vựng và ký hiệu - Phần 2: Thống kê ứng dụng
- 4 Tiêu chuẩn quốc gia TCVN 9603:2013 (ISO 5479:1997) về Giải thích dữ liệu thống kê - Kiểm nghiệm sai lệch so với phân bố chuẩn
- 5 Tiêu chuẩn quốc gia TCVN 9945-1:2013 (ISO 7870-1:2007) về Biểu đồ kiểm soát - Phần 1: Hướng dẫn chung
- 6 Tiêu chuẩn quốc gia TCVN 9944-3:2013 (ISO 22514-3:2008) về Phương pháp thống kê trong quản lý quá trình - Năng lực và hiệu năng- Phần 3: Nghiên cứu hiệu năng máy đối với dữ liệu được đo trên bộ phận riêng biệt
- 7 Tiêu chuẩn quốc gia TCVN 9945-2:2013 (ISO 7870-2:2013) về Biểu đồ kiểm soát - Phần 2: Biểu đồ kiểm soát Shewhart
- 8 Tiêu chuẩn quốc gia TCVN 9944-1:2013 (ISO 22514-1:2009) về Phương pháp thống kê trong quản lý quá trình - Năng lực và hiệu năng - Phần 1:Nguyên tắc chung và khái niệm
- 9 Tiêu chuẩn quốc gia TCVN 9944-7:2013 (ISO 22514-7:2012) về Phương pháp thống kê trong quản lý quá trình - Năng lực và hiệu năng - Phần 7: Năng lực của quá trình đo
- 10 Tiêu chuẩn quốc gia TCVN 9944-2:2018 (ISO 22514-2:2017) về Phương pháp thống kê trong quản lý quá trình - Năng lực và hiệu năng - Phần 2: Năng lực và hiệu năng quá trình của mô hình quá trình phụ thuộc thời gian
- 1 Tiêu chuẩn quốc gia TCVN 11864:2017 (ISO 18404:2015) về Phương pháp định lượng trong cải tiến quá trình - Six sigma - Năng lực của nhân sự chủ chốt và tổ chức khi triển khai six sigma và lean
- 2 Tiêu chuẩn quốc gia TCVN ISO/IEC 17025:2017 (ISO/IEC 17025:2017) về Yêu cầu chung về năng lực của phòng thử nghiệm và hiệu chuẩn
- 3 Tiêu chuẩn quốc gia TCVN ISO 17034:2017 (ISO 17034:2016) về Yêu cầu chung về năng lực của nhà sản xuất mẫu chuẩn
TIÊU CHUẨN QUỐC GIA
ISO 22514-4:2016
Statistical methods in process management - Capability and performance - Part 4: Process capability estimates and performance measures
Lời nói đầu
TCVN 9944-4:2018 thay thế TCVN 9944-4:2013.
TCVN 9944-4:2018 hoàn toàn tương đương với ISO 22514-4:2016.
TCVN 9944-4:2018 do Ban kỹ thuật tiêu chuẩn quốc gia TCVN/TC 69 Ứng dụng các phương pháp thống kê biên soạn, Tổng cục Tiêu chuẩn Đo lường Chất lượng đề nghị, Bộ Khoa học và Công nghệ công bố.
Bộ tiêu chuẩn TCVN 9944 (ISO 22514), Phương pháp thống kê trong quản lý quá trình - Năng lực và hiệu năng, gồm các tiêu chuẩn sau:
- TCVN 9944-1:2013 (ISO 22514-1:2009), Phần 1: Nguyên tắc chung và khái niệm;
- TCVN 9944-2:2018 (ISO 22514-2:2017), Phần 2: Năng lực và hiệu năng quá trình của các mô hình quá trình phụ thuộc thời gian;
- TCVN 9944-3:2013 (ISO 22514-3:2008), Phần 3: Nghiên cứu hiệu năng máy đối với dữ liệu đo được trên các bộ phận riêng biệt;
- TCVN 9944-4:2018 (ISO 22514-4:2016), Phần 4: Ước lượng năng lực quá trình và đo hiệu năng;
- TCVN 9944-6:2016 (ISO 22514-6:2013), Phần 6: Thống kê năng lực quá trình cho các đặc trưng có phân bố chuẩn đa biến;
- TCVN 9944-7:2013 (ISO 22514-7:2012), Phần 7: Năng lực của quá trình đo;
- TCVN 9944-8:2016 (ISO 22514-8:2014), Phần 8: Hiệu năng máy của quá trình sản xuất đa trạng thái.
Bộ tiêu chuẩn ISO 22514, Statistical methods in process management - Capability and performance, còn có tiêu chuẩn sau:
- Part 5: Process capability statistics for attribute characteristics
Lời giới thiệu
Nhiều tổ chức đã bắt tay vào chiến lược cải tiến liên tục. Để tuân thủ chiến lược này, mọi tổ chức đều cần đánh giá năng lực và hiệu năng của các quá trình quan trọng. Các phương pháp mô tả trong tiêu chuẩn này nhằm hỗ trợ nhà quản lý thực hiện việc này. Những đánh giá này cần được lãnh đạo xem xét thường xuyên để có thể thực hiện các hành động cải tiến liên tục phù hợp khi cần thiết.
Nội dung của tiêu chuẩn này có sự thay đổi lớn về quan điểm trong thời điểm hiện tại. Thay đổi cơ bản nhất là việc phân tách giữa khái niệm sử dụng trong tiêu chuẩn này là điều kiện năng lực với điều kiện hiệu năng, khác biệt chính là việc độ ổn định thống kê có thu được (năng lực) hay không (hiệu năng). Điều này dẫn đến hai tập hợp chỉ số được đề cập trong các điều liên quan. Việc chỉ ra sự phân biệt giữa các chỉ số này trở nên cần thiết vì thực tế trong ngành cho thấy các công ty đều làm hiểu sai về tình trạng năng lực thực sự của mình qua việc tính toán và công bố những chỉ số không phù hợp.
Tiến trình của tiêu chuẩn này đi từ điều kiện chung đến cụ thể và cách tiếp cận này dẫn đến công thức tổng quát được đưa ra trước những biểu thị thông thường nhưng cụ thể hơn của chúng.
Có nhiều tài liệu mô tả tầm quan trọng của việc thông hiểu các quá trình hoạt động trong tổ chức bất kỳ, là quá trình sản xuất hoặc xử lý thông tin. Khi các tổ chức cạnh tranh bán hàng với nhau, điều ngày càng trở nên rõ ràng là không chỉ giá thành chi trả cho sản phẩm hoặc dịch vụ là vấn đề lớn mà còn chi phí nào người mua phải chịu khi sử dụng sản phẩm hoặc dịch vụ đó. Mục tiêu cho mọi nhà cung cấp là liên tục giảm độ biến động và không chỉ dừng ở đáp ứng quy định.
Cải tiến liên tục dẫn đến giảm chi phí sai hỏng và hỗ trợ việc duy trì sự tồn tại trong thế giới cạnh tranh ngày một nhiều. Cũng có thể tiết kiệm các chi phí thẩm định vì độ biến động giảm thì nhu cầu kiểm tra sản phẩm có thể không cần thiết hoặc tần số lấy mẫu có thể giảm.
Đánh giá năng lực và hiệu năng quá trình là cần thiết để cho phép tổ chức đánh giá năng lực và hiệu năng của nhà cung cấp. Các tổ chức sẽ thấy những chỉ số trong tiêu chuẩn này rất hữu ích cho nỗ lực đó.
Định lượng độ biến động trong quá trình cho phép đánh giá sự phù hợp và khả năng đáp ứng yêu cầu cho trước nào đó của quá trình. Những nội dung dưới đây đưa ra triết lý cần được thông hiểu để xác định năng lực hoặc hiệu năng của quá trình bất kỳ.
Mọi quá trình đều có độ biến động vốn có nhất định. Tiêu chuẩn này không cố gắng giải thích ý nghĩa của độ biến động vốn có, vì sao nó tồn tại, nó bắt nguồn từ đâu cũng như ảnh hưởng của nó tới quá trình như thế nào. Tiêu chuẩn này bắt đầu từ tiền đề là nó tồn tại và ổn định.
Chủ sở hữu quá trình cần cố gắng hiểu những nguồn biến động trong các quá trình của mình. Các phương pháp như lưu đồ quá trình và xác định đầu vào, đầu ra của quá trình sẽ giúp nhận biết những độ biến động này cùng với việc sử dụng thích hợp biểu đồ nguyên nhân-kết quả (biểu đồ xương cá).
Điều quan trọng đối với người sử dụng tiêu chuẩn này là đánh giá được độ biến động tồn tại sẽ có bản chất ngắn hạn cũng như độ biến động có bản chất dài hạn và việc xác định năng lực chỉ sử dụng độ biến động ngắn hạn có thể khác biệt lớn so với sử dụng độ biến động dài hạn.
Khi xét độ biến động ngắn hạn, có thể tiến hành nghiên cứu chỉ sử dụng độ biến động ngắn hạn, đôi khi được gọi là nghiên cứu máy và được mô tả trong TCVN 9944-3 (ISO 22514-3). Phương pháp cần thiết để tiến hành nghiên cứu như vậy không thuộc phạm vi của tiêu chuẩn này; tuy nhiên, cần chú ý là các nghiên cứu đó rất quan trọng và hữu ích.
Cũng cần chú ý rằng khi các chỉ số năng lực trong tiêu chuẩn này được tính toán, đó chỉ là các ước lượng điểm cho giá trị thực của chúng. Do đó khuyến nghị rằng, khi có thể, cần tính toán và báo cáo khoảng tin cậy của các chỉ số. Tiêu chuẩn này mô tả các phương pháp để tính chúng.
PHƯƠNG PHÁP THỐNG KÊ TRONG QUẢN LÝ QUÁ TRÌNH - NĂNG LỰC VÀ HIỆU NĂNG - PHẦN 4: ƯỚC LƯỢNG NĂNG LỰC QUÁ TRÌNH VÀ ĐO HIỆU NĂNG
Statistical methods in process management - Capability and performance - Part 4: Process capability estimates and performance measures
Tiêu chuẩn này mô tả các thước đo năng lực và hiệu năng quá trình được sử dụng phổ biến.
2.1 Ký hiệu
Ngoài các ký hiệu được liệt kê dưới đây, một số ký hiệu được định nghĩa khi chúng được sử dụng trong văn bản.
α phần hoặc tỷ lệ
β tham số hình dạng của phân bố Weibull
β2 hệ số độ nhọn
c4 hằng số dựa trên cỡ nhóm con, n [xem TCVN 9945-2 (ISO 7870-2)]
Cp chỉ số năng lực quá trình
Cpk chỉ số năng lực tối thiểu quá trình
![]() chỉ số năng lực dưới của quá trình
chỉ số năng lực dưới của quá trình
![]() chỉ số năng lực trên của quá trình
chỉ số năng lực trên của quá trình
Cpm chỉ số năng lực thay thế của quá trình
CR tỉ số năng lực quá trình (PCF)
d2 hằng số dựa trên cỡ nhóm con, n [xem TCVN 9945-2 (ISO 7870-2)]
e số Euler (xấp xỉ 2,718), hằng số toán học
Φ hàm phân bố của phân bố chuẩn chuẩn hóa
γ tham số vị trí trong phân bố Weibull
γ1 hệ số bất đối xứng
m số nhóm con
Kl, Ku hệ số nhân dùng để ước lượng giới hạn tin cậy cho chỉ số năng lực quá trình
L giới hạn quy định dưới
P0,135 % phân vị 0,135 % dưới
µ vị trí của quá trình; giá trị trung bình tổng thể
N cỡ mẫu tổng
n số giá trị hoặc cỡ nhóm con (đối với biểu đồ kiểm soát)
Pα% phân vị α phần trăm
pL tỷ lệ không phù hợp dưới
Pp chỉ số hiệu năng quá trình
Ppk chỉ số hiệu năng tối thiểu quá trình
![]() chỉ số hiệu năng dưới của quá trình
chỉ số hiệu năng dưới của quá trình
![]() chỉ số hiệu năng trên của quá trình
chỉ số hiệu năng trên của quá trình
pt tỷ lệ không phù hợp toàn phần
pU tỷ lệ không phù hợp trên
P99,865 % phân vị 99,865 % trên
π hằng số hình học
Qk chỉ số biến động quá trình
θ tham số yêu cầu cho phân bố Rayleigh
![]() trung bình độ rộng nhóm con
trung bình độ rộng nhóm con
S độ lệch chuẩn, thống kê mẫu
St độ lệch chuẩn, với chỉ số dưới ‘t’ chỉ thị toàn phần
![]() trung bình độ lệch chuẩn mẫu
trung bình độ lệch chuẩn mẫu
Sj độ lệch chuẩn mẫu quan trắc của nhóm con thứ j
σ độ lệch chuẩn, tổng thể
![]() độ lệch chuẩn ước lượng, toàn phần
độ lệch chuẩn ước lượng, toàn phần
T giá trị đích
U giới hạn quy định trên
Xα% phân vị α %
Xi giá trị thứ i trong mẫu
![]() giá trị trung bình cộng, mẫu
giá trị trung bình cộng, mẫu
![]() trung bình cộng, của số trung bình cộng mẫu
trung bình cộng, của số trung bình cộng mẫu
ξ tham số thang đo trong phân bố Weibull
Y1, Y2 giá trị đọc từ biểu đồ
zα phân vị từ -∞ đến α của phân bố chuẩn chuẩn hóa
2.2 Chữ viết tắt
MSE sai số bình phương trung bình
PCF tỷ lệ năng lực quá trình
PCI chỉ số năng lực quá trình
3 Các khái niệm cơ bản được sử dụng cho năng lực và hiệu năng quá trình
3.1 Khái quát
Các thước đo đề cập trong 4.2 đến 4.6 chỉ đề cập đến dữ liệu đo được. Chúng có thể không thích hợp cho dữ liệu đếm hoặc định tính và thông tin liên quan đến trình bày thước đo cho dữ liệu như vậy sẽ được đề cập trong TCVN 9944-5 (ISO 22514-5).
3.2 Vị trí
Đặc trưng của vị trí là trung bình, µ, hoặc trung vị, X50 %. Mặc dù đối với các phân bố đối xứng trung bình là lựa chọn tự nhiên nhất, với các phân bố không đối xứng trung vị là lựa chọn ưu tiên.
3.3 Độ phân tán
3.3.1 Độ phân tán vốn có
Lựa chọn ưu tiên để định lượng độ phân tán vốn có là độ lệch chuẩn σ. Giá trị này thường được ước lượng từ giá trị độ rộng trung bình, ![]() , lấy từ biểu đồ độ rộng (R) hoặc
, lấy từ biểu đồ độ rộng (R) hoặc ![]() từ biểu đồ độ lệch chuẩn (S) khi quá trình ổn định và trong trạng thái kiểm soát thống kê như chỉ ra ở 4.1. Các phương pháp sử dụng để ước lượng độ lệch chuẩn quá trình được cho trong Phụ lục A.
từ biểu đồ độ lệch chuẩn (S) khi quá trình ổn định và trong trạng thái kiểm soát thống kê như chỉ ra ở 4.1. Các phương pháp sử dụng để ước lượng độ lệch chuẩn quá trình được cho trong Phụ lục A.
3.3.2 Độ phân tán tổng thể
Cần phân biệt giữa độ lệch chuẩn chỉ đo độ biến động ngắn hạn và độ lệch chuẩn đo độ biến động dài hạn. Độ phân tán tổng thể là độ phân tán vốn có trong độ biến động dài hạn. Các phương pháp tính độ lệch chuẩn thể hiện các biến động này được cho trong Phụ lục A. Thông thường, khi dữ liệu được thu thập trong khoảng thời gian dài, độ lệch chuẩn sẽ lớn hơn do ảnh hưởng của các dao động trong quá trình, σt.
3.3.3 Độ phân tán ngắn hạn
Quá trình có thể có hiệu ứng phân tán ngắn hạn là một phần của độ phân tán tổng thể. Hình 1 minh họa điều này. Độ phân tán ngắn hạn bao gồm độ phân tán vốn có và cũng có thể bao gồm một số hiệu ứng không ổn định ngắn hạn.
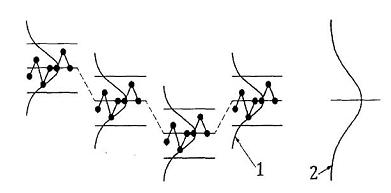
CHÚ DẪN
1 độ phân tán ngắn hạn
2 độ phân tán tổng thể
Hình 1 - Độ phân tán ngắn hạn và mối quan hệ của nó với độ phân tán tổng thể
Độ phân tán tổng thể có thể có hình dạng bất kỳ và không nhất thiết phải là chuẩn như được minh họa ở đây.
3.4 Sai số bình phương trung bình (MSE)
Một số người thực hành sử dụng sai số bình phương trung bình làm thước đo ưu tiên khi giảm thiểu độ biến động. Nó tương thích với phương pháp sử dụng trong kỹ thuật chất lượng không trực tuyến.
3.5 Giới hạn quy chiếu
Giới hạn quy chiếu dưới và trên được xác định tương ứng là phân vị 0,135 % và 99,865 % của phân bố mô tả đầu ra của đặc trưng quá trình. Chúng được viết là X0,135 5 % và X99,865 %.
3.6 Khoảng quy chiếu (còn gọi là độ trải quá trình)
Khoảng quy chiếu là khoảng giữa giới hạn quy chiếu trên và dưới. Khoảng quy chiếu gồm 99,73 % cá thể trong tổng thể từ quá trình ở trạng thái kiểm soát thống kê.
Năng lực quá trình là thước đo độ biến động vốn có của quá trình. Độ biến động luôn có trong quá trình nhưng khi hoạt động ở trạng thái kiểm soát thống kê thì được gọi là độ biến động vốn có của quá trình. Nó thể hiện độ biến động còn lại sau khi đã loại bỏ tất cả các nguyên nhân ấn định có thể loại bỏ. Nếu quá trình được theo dõi bằng biểu đồ kiểm soát, biểu đồ kiểm soát sẽ thể hiện trạng thái được kiểm soát.
Năng lực thường được coi là liên quan đến tỷ lệ đầu ra sẽ xuất hiện trong phạm vi dung sai quy định của sản phẩm. Vì quá trình ở trạng thái kiểm soát thống kê cần được mô tả bằng phân bố có thể dự đoán nên có thể ước lượng tỷ lệ đầu ra nằm ngoài quy định. Với điều kiện quá trình duy trì ở trạng thái kiểm soát thống kê, nó sẽ tiếp tục tạo ra cùng một tỷ lệ nằm ngoài quy định.
Các hoạt động quản lý để giảm độ biến động do nguyên nhân ngẫu nhiên đòi hỏi cải thiện năng lực của quá trình nhằm đáp ứng các yêu cầu quy định một cách nhất quán.
Nói ngắn gọn, cần thực hiện những điều sau:
- xác định quá trình và điều kiện vận hành của nó. Nếu có thay đổi so với các điều kiện này thì cần có một nghiên cứu về quá trình mới;
- đánh giá độ biến động đo lường ngắn hạn và dài hạn theo phần trăm độ biến động tổng thể và giảm thiểu chúng;
- duy trì tính ổn định của quá trình và duy trì trạng thái kiểm soát thống kê của nó;
- ước lượng độ biến động vốn có còn lại;
- chọn thước đo năng lực phù hợp.
Dưới đây là các điều kiện sẽ áp dụng cho năng lực:
- tất cả các điều kiện kỹ thuật, ví dụ nhiệt độ và độ ẩm, phải được nêu rõ;
- độ không đảm bảo của hệ thống đo phải được ước lượng và đánh giá thích hợp (xem TCVN 9944-7 (ISO 22514-7);
- các khía cạnh nhiều yếu tố, nhiều mức của quá trình cần được cho phép;
- khoảng thời gian thu thập dữ liệu phải được ghi lại;
- tần số lấy mẫu phải được quy định và ngày bắt đầu và ngày kết thúc việc thu thập dữ liệu;
- quá trình phải được kiểm soát bằng biểu đồ kiểm soát;
- quá trình phải ở trạng thái kiểm soát thống kê.
Cần kiểm tra biểu đồ kiểm soát từ đó dữ liệu được lấy cho kiểm soát thống kê và kiểm tra biểu đồ dữ liệu theo giới hạn quy định bất kỳ áp dụng cho nó. Kiểm nghiệm hiệu lực đối với tính chuẩn cần được sử dụng trong việc đánh giá dữ liệu, ví dụ như kiểm nghiệm Anderson-Darling[15] hoặc phương pháp thích hợp khác bất kỳ. Kiểm nghiệm này có hiệu lực trong việc phát hiện độ lệch so với tính chuẩn ở đuôi của phân bố và được gợi ý ở đây vì đó là khu vực quan tâm đối với chỉ số năng lực và hiệu năng. Ngoài ra, có thể sử dụng giấy xác suất chuẩn để tìm:
a) kiểm tra xác nhận tính chuẩn;
b) giá trị bất thường;
c) dữ liệu nằm ngoài giới hạn quy định bất kỳ;
d) dữ liệu có nằm hoàn toàn trong giới hạn quy định hay không;
e) bằng chứng về bất đối xứng (nghĩa là độ bất đối xứng);
f) bằng chứng về “đuôi dài” trong dữ liệu (nghĩa là độ nhọn);
g) phân bố lệch tâm; và
h) đặc trưng bất thường bất kỳ.
Cần giải thích về những bất thường trong mối quan hệ với các đặc trưng đề cập ở trên và thực hiện hành động thích hợp đối với dữ liệu trước khi tính toán thước đo bất kỳ. Sẽ không thích hợp nếu chỉ loại bỏ dữ liệu thể hiện không phù hợp với dạng dự kiến bất kỳ. Những sai lệch như vậy có thể bộc lộ nhiều về biểu hiện của quá trình và cần được nghiên cứu kỹ.
4.2.1 Phân bố chuẩn
Năng lực quá trình được định nghĩa là thước đo thống kê độ biến động vốn có của quá trình đối với một đặc trưng cho trước. Phương pháp truyền thống là lấy khoảng quy chiếu mô tả 99,73 % giá trị cá thể từ quá trình nằm trong trạng thái kiểm soát thống kê với 0,135 % còn lại về mỗi phía. Điều này áp dụng ngay cả khi tổng thể các giá trị cá thể không có phân bố chuẩn. Đối với phân bố chuẩn, khoảng quá trình này được đại diện bởi sáu độ lệch chuẩn. Xem Hình 2.
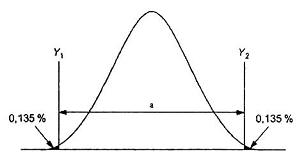
CHÚ DẪN
a Khoảng quy chiếu 99,73 %.
Hình 2 - Phân bố chuẩn
Đôi khi, năng lực quá trình được tính thêm các nguồn biến động khác như quá trình nhiều dòng, ví dụ, đầu ra từ quá trình ép đúc phun nhiều ngăn. Trong những trường hợp này, phân bố các giá trị từ tất cả các ngăn có thể vẫn xấp xỉ chuẩn nhưng có thêm độ biến động để độ lệch chuẩn phải thể hiện độ biến động toàn phần, σt. Điều quan trọng là nêu rõ cách tính toán độ lệch chuẩn cũng như chiến lược lấy mẫu được sử dụng, cỡ mẫu, số lượng và độ biến động của đầu ra sản xuất giữa các mẫu vì điều này sẽ ảnh hưởng đến hiệu lực của việc đánh giá năng lực trong thực tế [xem thêm TCVN 9944-2 (ISO 22514-2)].
Dữ liệu sẽ thường được lấy từ biểu đồ kiểm soát. Nếu biểu đồ kiểm soát có đường kiểm soát nới lỏng hoặc thay đổi thì độ lệch chuẩn quá trình thực sẽ lớn hơn so với ước lượng từ dữ liệu lấy từ biểu đồ kiểm soát có đường kiểm soát tiêu chuẩn. Các vấn đề như vậy và những vấn đề nêu trước đó sẽ ảnh hưởng đến khoảng quy chiếu và điều quan trọng là chúng được nêu rõ trong bất kỳ đánh giá năng lực nào.
Quá trình có “năng lực” sẽ là những quá trình có khoảng quy chiếu nhỏ hơn dung sai quy định một lượng nhất định. Ví dụ về điều này được thể hiện trên Hình 3.
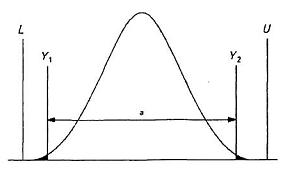
CHÚ DẪN
a Khoảng quy chiếu 99,73 %.
Hình 3 - Phân bố chuẩn với giới hạn quy định
4.2.2 Phân bố không chuẩn
Nếu phân bố các giá trị cá thể không tạo thành phân bố chuẩn mà đối xứng lệch thì khoảng quy chiếu có thể có dạng như trên Hình 4. Giá trị Y1 và Y2 thường là các phân vị 0,135 % và 99,865 %, có thể ước lượng bằng cách sử dụng giấy xác suất phù hợp (xem Hình 5 về ví dụ sử dụng giấy xác suất phân bố giá trị cực trị) hoặc bằng cách sử dụng phần mềm máy tính phù hợp. Chúng cũng có thể được tính bằng cách sử dụng các giá trị được lập bảng (xem Phụ lục B) hoặc sử dụng hàm xác suất cụ thể như gợi ý trong Phụ lục C.
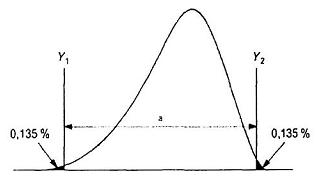
CHÚ DẪN
a Khoảng quy chiếu 99,73 %.
Hình 4 - Phân bố không chuẩn
Ngay cả khi quá trình được coi là có năng lực theo định nghĩa nêu trên (4.2.1), nếu phân bố quá trình định tâm kém so với giới hạn quy định thì vẫn có thể tạo ra các cá thể nằm ngoài quy định. Vì lý do này, cần đánh giá vị trí cùng với khoảng quá trình.
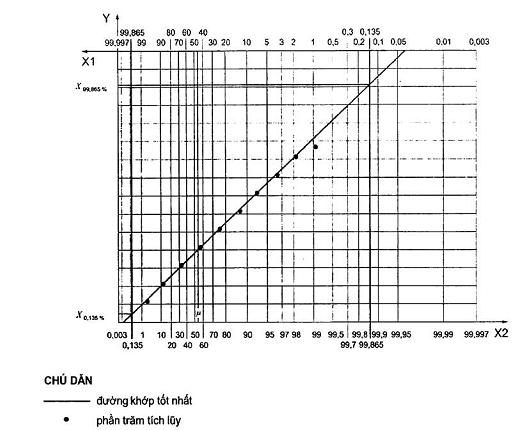
Hình 5 - Ví dụ sử dụng giấy xác suất phân bố giá trị cực trị
4.4 Chỉ số năng lực quá trình đối với dữ liệu đo được
4.4.1 Khái quát
Cần lưu ý là khi chỉ số năng lực cho trong tiêu chuẩn này được tính toán, chứng chỉ tạo thành các ước lượng điểm cho các giá trị thực của chúng. Vì vậy, khuyến nghị bất cứ khi nào có thể, cần tính và báo cáo khoảng tin cậy của các chỉ số. Phương pháp tính toán được mô tả trong Phụ lục D.
Sẽ hiệu quả khi biểu thị năng lực quá trình bằng cách sử dụng số chỉ số. Có nhiều chỉ số được đưa ra. Phải thận trọng khi xử lý các phân bố không chuẩn.
Chỉ số năng lực quá trình chỉ được thiết lập cho quá trình thống kê “được kiểm soát”.
Chỉ số năng lực quá trình thường được sử dụng là tỷ số giữa dung sai quy định với khoảng quy chiếu và được ký hiệu là Cp. Do đó:
|
| (1) |
Có các chỉ số khác kết hợp cả vị trí và độ biến động. Trong đó, chỉ số được sử dụng rộng rãi nhất là Cpk. Nếu chỉ số quan trắc nhỏ hơn giá trị quy định, thì quá trình được coi là không thể chấp nhận và có thể dẫn đến việc chuyển dịch tỷ lệ cá thể nằm ngoài quy định hoặc hàm đó và sự làm khớp có thể được thỏa hiệp.
Chỉ số Cpk là tỷ số của hiệu giữa giới hạn dung sai quy định và vị trí quá trình với hiệu giữa giới hạn quá trình tự nhiên tương ứng và vị trí quá trình.
|
| (2) |
và
|
| (2) |
Chỉ số Cpk được báo cáo là giá trị nhỏ hơn trong hai giá trị này.
CHÚ THÍCH : Một số người thực hành báo cáo cả hai giá trị nêu trên (chúng còn được gọi tương ứng là CPU và CPL). Điều này cung cấp thông tin về cả hai phía của quá trình.
Các chỉ số này sẽ cung cấp thông tin về việc quá trình định tâm kém hay không và việc nó có khả năng tạo ra các cá thể nằm ngoài quy định hay không. Ngay cả khi chỉ số Cp cao thì giá trị chỉ số Cpk thấp sẽ thể hiện quá trình định tâm kém và xác suất cao trong việc tạo ra các cá thể nằm ngoài quy định.
4.4.2 Chỉ số Cp (đối với phân bố chuẩn)
Nếu các giá trị cá thể hình thành phân bố chuẩn và thu được từ một quá trình ổn định thống kê, thì độ dài khoảng quy chiếu bằng 6σ, trong đó σ là độ lệch chuẩn vốn có của quá trình. Vì vậy, chỉ số Cp có thể được biểu thị là:
![]()
Ước lượng ![]() độ lệch chuẩn vốn có của quá trình (σ) được yêu cầu để thu được ước lượng của chỉ số Cp. Khi có được giá trị này, thường cùng với dữ liệu từ biểu đồ kiểm soát khi quá trình chứng tỏ sự ổn định thống kê (xem 4.1), chỉ số được ước lượng:
độ lệch chuẩn vốn có của quá trình (σ) được yêu cầu để thu được ước lượng của chỉ số Cp. Khi có được giá trị này, thường cùng với dữ liệu từ biểu đồ kiểm soát khi quá trình chứng tỏ sự ổn định thống kê (xem 4.1), chỉ số được ước lượng:
![]()
4.4.3 Chỉ số Cpk (đối với phân bố chuẩn)
Khi phân bố của các giá trị cá thể hình thành phân bố chuẩn, trung vị X50 % bằng trung bình (µ). Ngoài ra, X99,865 % - X50 % và X50 % - X0,135 % đều bằng 3σ. Vì vậy, chỉ số Cpk có thể được biểu thị là giá trị tối thiểu của:
![]()
hoặc
![]()
Cpk ước lượng (bằng cách dùng ![]() để ước lượng µ thay vì X50 %) sẽ là giá trị tối thiểu của:
để ước lượng µ thay vì X50 %) sẽ là giá trị tối thiểu của:
![]()
hoặc
![]()
Khi tính toán chỉ số năng lực, phải tính đến thước đo độ biến động quá trình sử dụng ở mẫu số. Ở đây, σ được cho để thể hiện độ biến động khi dữ liệu thu được từ quá trình ở trạng thái kiểm soát thống kê.
Dữ liệu có thể thu được từ quá trình nhiều dòng như máy nhiều đầu cấp liệu hoặc máy đa trục trong đó đầu ra tổng thể được xử lý cùng nhau, khi dữ liệu từ tất cả các dòng được xem xét đồng thời. Chỉ số này càng nhỏ thì tỷ lệ cá thể sản xuất nằm ngoài quy định càng cao.
4.4.4 Chỉ số Cpk đối với dung sai một phía
Khi chỉ có một giới hạn quy định cho trước, thì chỉ có thể tính chỉ số Cpk. Chỉ số sẽ được tính bằng cách sử dụng giới hạn phù hợp, L hoặc U.
4.5 Chỉ số năng lực quá trình đối với dữ liệu đo được (không chuẩn)
4.5.1 Khái quát
Nếu phân bố của các giá trị cá thể không phải là phân bố chuẩn thì vẫn áp dụng Công thức (1) và (2) nhưng việc ước lượng các chỉ số trở nên phức tạp hơn. Có ba cách ước lượng giới hạn quy chiếu được nêu ở đây.
Phương pháp giấy xác suất nêu trong 4.5.2 khá đơn giản và đòi hỏi ít tính toán nhưng hơi thô. Cách tiếp cận nêu ở 4.5.4 liên quan đến nhiều tính toán nhưng ưu việt hơn các phương pháp khác bất kỳ về độ chính xác.
4.5.2 Phương pháp giấy xác suất
Từ biểu đồ tương tự như thể hiện trên Hình 4, có thể thu được ước lượng của các phân vị X0,135 % và X99,865 %. Các ước lượng được ký hiệu tương ứng là Y1 và Y2, Công thức (1) trở thành:
![]()
Theo cách tương tự, công thức tính Cpk trở thành:
![]()
hoặc
![]()
tùy theo công thức nào cho giá trị thấp hơn.
Nếu chỉ số quan trắc nhỏ hơn giá trị quy định thì quá trình được coi là không thể chấp nhận và có thể dẫn đến việc chuyển dịch một tỷ lệ cá thể nằm ngoài quy định hoặc hàm đó và sự làm khớp có thể được thỏa hiệp. Tỷ lệ không phù hợp phụ thuộc vào phân bố và giá trị của chỉ số. Liên hệ giữa chỉ số và tỷ lệ cá thể không phù hợp tạo ra phụ thuộc vào lớp phân bố. Cần cẩn trọng để không giải thích các chỉ số trên cơ sở các điểm ngưỡng được rút ra cho phân bố chuẩn và do đó chỉ áp dụng được cho phân bố đó.
Chú ý là phương pháp giấy xác suất ước lượng trực tiếp các phân vị cực trị và có thể không chính xác.
4.5.3 Phương pháp đường cong Pearson
Có thể sử dụng đường Pearson chuẩn hóa như một lựa chọn thay thế cho giấy xác suất. Phương pháp này được mô tả bằng ví dụ (xem Phụ lục B). Chỉ số được tính toán theo công thức:
![]()
trong đó, ![]() và
và ![]() là phân vị 0,135 % và 99,865 % ước lượng từ đường Pearson chuẩn hóa.
là phân vị 0,135 % và 99,865 % ước lượng từ đường Pearson chuẩn hóa.
Ta cũng có công thức:
![]()
hoặc
![]()
trong đó, ![]() là trung vị ước lượng.
là trung vị ước lượng.
Để sử dụng phương pháp này, cần thiết lập giá trị bất đối xứng và độ nhọn cùng với trung bình và độ lệch chuẩn cho tập dữ liệu dùng để tính toán chỉ số.
Phương pháp này không được ưa dùng nhưng được trình bày ở đây cho hoàn chỉnh vì đôi khi cũng được sử dụng.
Cách tiếp cận này, và loại tương tự dựa trên đường Johnson, cần được xem xét cẩn trọng, đặc biệt khi qui trình nằm trong chương trình máy tính “hộp đen” dùng để phân tích các tập dữ liệu lớn. Có thể có một số khó khăn như:
- trong hệ phân bố, một số phân bố sẽ khó làm khớp hơn so với các phân bố khác. Phương pháp mômen có thể đưa ra các tham số đường cong không ổn định hoặc không hiệu quả trong một số trường hợp;
- nếu kỹ thuật ước lượng được áp dụng không chuyên nghiệp thì có thể thu được đường cong khớp không có ý nghĩa trong phạm vi dữ liệu nhất định. Ví dụ, với phương pháp mômen, lỗi dễ mắc phải là làm khớp phân bố Pearson Loại III có ngưỡng ước lượng nhỏ hơn biên dưới đối với đầu ra quá trình, từ đó làm mất hiệu lực các ước lượng của X0,135 % và Cpk;
- phương pháp mômen không mang lại ước lượng độ biến động của chỉ số ước lượng. Tương tự, phương pháp này không đưa ra khoảng tin cậy cho các chỉ số;
- không phải mọi phân bố dữ liệu đều có thể mô tả thích hợp bằng đường Pearson hoặc Johnson;
- kiểm nghiệm tính phù hợp chỉ giới hạn ở kiểm nghiệm Khi bình phương vì thường không có sẵn các kiểm nghiệm có hiệu lực hơn cho hệ Pearson và Johnson;
- cách tiếp cận “hộp đen” có xu hướng thay thế các thực hành cơ bản, như vẽ đồ thị dữ liệu và áp dụng các phép biến đổi chuẩn hóa đơn giản, cung cấp hiểu biết xác thực về quá trình.
4.5.4 Phương pháp xác định phân bố
Phụ lục C mô tả các họ hàm phân bố nhất định (như phân bố loga chuẩn, Rayleigh và Weibull) phổ biến khi nghiên cứu về năng lực quá trình. Phương pháp này trước hết để xác định họ phân bố thích hợp, thứ hai là ước lượng tham số của phân bố thuộc họ có thể giải thích tốt nhất dữ liệu bằng phương pháp ước lượng hiệu quả nhất định và cuối cùng là biểu thị các đại lượng dưới dạng tham số của phân bố đó.
Điều này tương tự như quy trình được chọn trong trường hợp phân bố chuẩn, trong đó σ được ước lượng và 6σ được đại diện bởi (X99,865% - X0,135%).
Các loại giấy xác suất khác nhau có thể hữu ích cho việc xác định họ phân bố thích hợp.
4.6 Phương pháp thay thế để mô tả và tính toán ước lượng năng lực quá trình
Cơ sở của phương pháp này là các định nghĩa được sử dụng rộng rãi về Cp và Cpk cho “quá trình lý tưởng” với đặc trưng phân bố chuẩn X, trong đó kỳ vọng µ và phương sai σ2 không đổi theo thời gian và các ước lượng tương ứng là ![]() và S2.
và S2.
Bảng 1 - Chỉ số và ước lượng năng lực quá trình đối với phân bố chuẩn
| Chỉ số | Ước lượng |
|
|
|
|
|
|
|
|
|
|
|
|
“Quá trình lý tưởng” này hàm ý là độ lệch chuẩn dài hạn bằng độ lệch chuẩn ngắn hạn.
Đối với phân bố chuẩn, có mối quan hệ chính xác giữa tỷ lệ các đơn vị không phù hợp dưới với ![]() và giữa tỷ lệ không phù hợp trên với
và giữa tỷ lệ không phù hợp trên với ![]() . Mối quan hệ này được thể hiện trong 4.8 để tính tỷ lệ nằm ngoài quy định từ chỉ số năng lực quá trình dưới và trên. Mối quan hệ đó được trình bày trong Bảng 2 để dễ dàng tham khảo.
. Mối quan hệ này được thể hiện trong 4.8 để tính tỷ lệ nằm ngoài quy định từ chỉ số năng lực quá trình dưới và trên. Mối quan hệ đó được trình bày trong Bảng 2 để dễ dàng tham khảo.
Khi các thước đo năng lực quá trình này được mở rộng cho các đặc trưng không có phân bố chuẩn, tỷ lệ cá thể không phù hợp có thể được chuyển thành chỉ số năng lực bằng cách sử dụng mối quan hệ trong Bảng 2. Cụ thể phương pháp này có thể được áp dụng nếu đặc trưng sản phẩm là định tính.
Bảng 2 - Chỉ số và ước lượng năng lực quá trình đối với phân bố chuẩn - Công thức tương đương
| Chỉ số | Ước lượng |
|
|
|
|
|
|
|
|
|
trong đó pU và pL là tỷ lệ không phù hợp ở giới hạn quy định trên và dưới, còn ![]() ,
, ![]() là các ước lượng tương ứng. Công thức trong bảng trên có thể áp dụng cho mọi phân bố.
là các ước lượng tương ứng. Công thức trong bảng trên có thể áp dụng cho mọi phân bố.
Giả định rằng người sử dụng có hiểu biết về hình dạng phân bố do những điều được biết về quá trình sản xuất hoặc nhờ đánh giá nhất định về mẫu bằng giấy xác suất thích hợp.
Đối với những phân bố được quan trắc thường xuyên (chuẩn, loga chuẩn, Rayleigh và Weibull), các quan hệ và công thức cần thiết được cho trong Phụ lục C.
4.7 Thước đo năng lực khác đối với dữ liệu liên tục
4.7.1 Tỷ số năng lực quá trình (PCF)
PCF là nghịch đảo của chỉ số Cp:
![]()
Tỷ số này có thể được biểu thị bằng giá trị phần trăm và thường được gọi là CR (%).
4.7.2 Chỉ số khi giới hạn quy định một phía hoặc không cho trước giới hạn quy định
4.7.2.1 Khái quát
Đôi khi, giới hạn quy định được cho chỉ có một giới hạn, ví dụ như giá trị lớn nhất. Trong trường hợp này, sẽ chỉ có thể tính chỉ số Cpk hoặc Ppk.
Cũng sẽ có tình huống giới hạn quy định không được cho trước hoặc không biết. Tuy nhiên, nếu giá trị đích hoặc danh nghĩa được cho đối với đặc trưng sản phẩm hoặc tham số quá trình thì các thước đo dưới đây có thể thích hợp. Chúng có giá trị đặc biệt với những người tham gia vào việc giảm thiểu độ biến động quá trình quanh giá trị đích.
4.7.2.2 Sai số bình phương trung bình (MSE)
Sai số bình phương trung bình cung cấp thước đo liên quan đến cả vị trí và độ biến động. Nó được tính như sau:
![]()
Khi rút ra thước đo này từ dữ liệu, cần cung cấp ước lượng độ lệch chuẩn quá trình và µ bằng cách sử dụng dữ liệu mẫu từ biểu đồ kiểm soát.
4.7.2.3 Chỉ số Qk
Chỉ số này sử dụng sai số bình phương trung bình nêu trong 4.7.2.2 nhưng biểu thị toàn bộ giá trị như hệ số của độ biến động và được tính như sau:
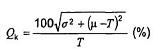
với T ≠ 0.
Một tính chất hay của chỉ số này là nếu quá trình trôi khỏi đích của nó thì chỉ số sẽ tăng giá trị và nếu độ biến động quá trình tăng thì cũng sẽ làm tăng giá trị của chỉ số. Chỉ số này càng nhỏ thì quá trình càng được coi là vận hành tốt.
4.7.2.4 Chỉ số Cpm
Chỉ số Cpm, giống như chỉ số Qk, kết hợp giá trị đích và MSE vào tính toán.
Ở dạng đơn giản nhất, chỉ số là:
![]()
Tính toán này có nghĩa T là điểm giữa giữa U và L và do đó đưa ra sự sàng lọc cho phép đối với giá trị không trung tâm T:
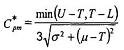
So sánh với chỉ số thông thường, Cp và Cpk, ở đây chỉ cần một chỉ số để mô tả tình huống.
Đôi khi chỉ số Cpm được gọi là chỉ số Taguchi vì sự kết hợp của MSE trong mẫu số.
4.8 Đánh giá tỷ lệ nằm ngoài quy định (phân bố chuẩn)
Tỷ lệ cá thể nằm ngoài quy định (pU và pL) nằm dưới L và trên U có thể ước lượng bằng cách sử dụng các tính chất của phân bố chuẩn chuẩn hóa. Độ lệch chuẩn hóa có thể được tính như sau:
![]()
và
![]()
![]() và
và ![]() tìm được là tỷ lệ vượt quá
tìm được là tỷ lệ vượt quá ![]() và
và ![]() tương ứng trong phân bố chuẩn chuẩn hóa.
tương ứng trong phân bố chuẩn chuẩn hóa.
Ngoài ra, hiệu suất quá trình có thể được tính là 100 % trừ đi tổng phần trăm không phù hợp, trong trường hợp quá trình được kiểm soát.
Nếu đặc trưng, được kiểm soát thống kê và ổn định, có ![]() là 0,86 và
là 0,86 và ![]() là 0,91 thì tỷ lệ nằm ngoài quy định có thể được xác định bằng cách sử dụng phương pháp nêu trên như dưới đây.
là 0,91 thì tỷ lệ nằm ngoài quy định có thể được xác định bằng cách sử dụng phương pháp nêu trên như dưới đây.
a) Tính độ lệch chuẩn hóa “dưới”:
![]()
= 3 x 0,91
= 2,73
b) Tính độ lệch chuẩn hóa “trên”:
![]()
= 3 x 0,86
= 2,58
c) Sử dụng phân bố chuẩn chuẩn hóa, tra hoặc tính giá trị ![]() và
và ![]() đối với tỷ lệ phân bố nằm ngoài giới hạn quy định U và L, zpU và zpL tương ứng.
đối với tỷ lệ phân bố nằm ngoài giới hạn quy định U và L, zpU và zpL tương ứng.
Để thuận tiện và dễ sử dụng, Bảng 3 đưa ra giá trị tra cứu cho tỷ lệ nằm ngoài quy định ước lượng. Bảng 3 được xác định theo ![]() hoặc
hoặc ![]() , chỉ số năng lực quá trình (PCI). Không nên sử dụng Bảng 3 để rút ra giá trị Cp hay Cpk cho dữ liệu định tính.
, chỉ số năng lực quá trình (PCI). Không nên sử dụng Bảng 3 để rút ra giá trị Cp hay Cpk cho dữ liệu định tính.
Sử dụng ví dụ ở trên với ![]() là 0,86 và
là 0,86 và ![]() là 0,91, có thể đọc trực tiếp trên Bảng 3 tỷ lệ ước lượng nằm ngoài giới hạn quy định U và L là 0,004 9 và 0,003 2.
là 0,91, có thể đọc trực tiếp trên Bảng 3 tỷ lệ ước lượng nằm ngoài giới hạn quy định U và L là 0,004 9 và 0,003 2.
Bảng 3 - ![]() hoặc
hoặc ![]() (PCI trong bảng) và tỷ lệ phân bố chuẩn còn lại trong đuôi của phân bố nằm ngoài giới hạn quy đỊnh
(PCI trong bảng) và tỷ lệ phân bố chuẩn còn lại trong đuôi của phân bố nằm ngoài giới hạn quy đỊnh
| PCI | 0,00 | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 |
| 1,6 | 7,9 x 10-07 | 6,8 x 10-07 | 5,9 x 10-07 | 5,0 x 10-07 | 4,3 x 10-07 | 3,7 x 10-07 | 3,2 x 10-07 | 2,7 x 10-07 | 2,3 x 10-07 | 2,0 x 10-07 |
| 1,5 | 3,4 x 10-06 | 3,0 x 10-06 | 2,6 x 10-06 | 2,2 x 10-06 | 1,9 x 10-06 | 1,7 x 10-06 | 1,4 x 10-06 | 1,2 x 10-06 | 1,1 x 10-06 | 9,2 x 10-07 |
| 1,4 | 1,3 x 10-05 | 1,2 x 10-05 | 1,0 x 10-05 | 8,9 x 10-06 | 7,8 x 10-06 | 6,8 x 10-06 | 5,9 x 10-06 | 5,2 x 10-06 | 4,5 x 10-06 | 3,9 x 10-06 |
| 1,3 | 4,8 x 10-05 | 4,2 x 10-05 | 3,7 x 10-05 | 3,3 x 10-05 | 2,9 x 10-05 | 2,6 x 10-05 | 2,3 x 10-05 | 2,0 x 10-05 | 1,7 x 10-05 | 1,5 x 10-05 |
| 1,2 | 0,000 2 | 0,000 1 | 0,000 1 | 0,000 1 | 0,000 1 | 0,000 1 | 0,000 1 | 0,000 1 | 0,000 1 | 0,000 1 |
| 1,1 | 0,000 5 | 0,000 4 | 0,000 4 | 0,000 3 | 0,000 3 | 0,000 3 | 0,000 3 | 0,000 2 | 0,000 2 | 0,000 2 |
| 1,0 | 0,001 3 | 0,001 2 | 0,001, 1 | 0,001 0 | 0,000 9 | 0,000 8 | 0,000 7 | 0,000 7 | 0,000 6 | 0,000 5 |
| 0,9 | 0,003 5 | 0,003 2 | 0,002 9 | 0,002 6 | 0,002 4 | 0,002 2 | 0,002 0 | 0,001 8 | 0,001 6 | 0,001 5 |
| 0,8 | 0,008 2 | 0,007 5 | 0,006 9 | 0,006 4 | 0,005 9 | 0,005 4 | 0,004 9 | 0,004 5 | 0,004 1 | 0,003 8 |
| 0,7 | 0,017 9 | 0,016 6 | 0,015 4 | 0,014 3 | 0,031 2 | 0,012 2 | 0,011 3 | 0,010 4 | 0,009 6 | 0,008 9 |
| 0,6 | 0,035 9 | 0,033 6 | 0,031 4 | 0,029 4 | 0,027 4 | 0,025 6 | 0,023 9 | 0,022 2 | 0,020 7 | 0,019 2 |
| 0,5 | 0,066 8 | 0,063 0 | 0,059 4 | 0,055 9 | 0,052 6 | 0,049 5 | 0,046 5 | 0,043 6 | 0,040 9 | 0,038 4 |
| 0,4 | 0,115 1 | 0,109 3 | 0,103 8 | 0,098 5 | 0,093 4 | 0,088 5 | 0,083 8 | 0,079 3 | 0,074 9 | 0,070 8 |
| 0,3 | 0,184 1 | 0,176 2 | 0,168 5 | 0,161 1 | 0,153 9 | 0,146 9 | 0,140 1 | 0,133 5 | 0,127 1 | 0,121 0 |
| 0,2 | 0,274 3 | 0,264 3 | 0,254 6 | 0,245 1 | 0,235 8 | 0,226 6 | 0,217 7 | 0,209 0 | 0,200 5 | 0,192 2 |
| 0,1 | 0,382 1 | 0,370 7 | 0,359 4 | 0,348 3 | 0,337 2 | 0,326 4 | 0,315 6 | 0,305 0 | 0,294 6 | 0,284 3 |
| 0,0 | 0,500 0 | 0,488 0 | 0,476 1 | 0,464 1 | 0,452 2 | 0,440 4 | 0,428 6 | 0,416 8 | 0,405 2 | 0,393 6 |
Hiệu năng quá trình đối với một đặc trưng là phân bố kết quả thu được. Khác biệt quan trọng duy nhất giữa hiệu năng và năng lực là đối với hiệu năng, không có yêu cầu quá trình ở trạng thái kiểm soát thống kê hay quá trình được kiểm soát bằng biểu đồ kiểm soát. Dưới đây là các điều kiện sẽ áp dụng cho hiệu năng:
- tất cả các điều kiện kỹ thuật, ví dụ nhiệt độ và độ ẩm, phải được nêu rõ;
- độ không đảm bảo của hệ thống đo phải được ước lượng và đánh giá thích hợp [xem TCVN 9944-7 (ISO 22514-7)];
- các khía cạnh nhiều yếu tố, nhiều mức của quá trình cần được xét đến;
- khoảng thời gian thu thập dữ liệu phải được ghi lại;
- tần số lấy mẫu phải được quy định và ngày bắt đầu và ngày kết thúc việc thu thập dữ liệu;
- quá trình không cần phải được kiểm soát bằng biểu đồ kiểm soát;
- quá trình không cần phải ở trạng thái kiểm soát thống kê, đặc biệt, có thể sử dụng dữ liệu lịch sử chưa biết về trình tự để đánh giá hiệu năng quá trình.
Các chỉ số được cho dưới đây để biểu thị hiệu năng quá trình. Dạng của chúng tương tự như đã cho trong nội dung về năng lực và sử dụng mối quan hệ tổng quát trong Công thức (1) và (2) đối với dữ liệu đo được ngoại trừ chúng được gọi tương ứng là Pp, PpkU và PpkL.
5.2 Chỉ số hiệu năng quá trình đối với dữ liệu đo được (phân bố chuẩn)
5.2.1 Chỉ số Pp
Khi các giá trị cá thể hình thành phân bố chuẩn, độ dài khoảng quy chiếu bằng 6 σt, trong đó σt là độ lệch chuẩn toàn phần. Vì vậy, chỉ số Pp có thể được biểu thị là:
![]()
Ước lượng ![]() độ lệch chuẩn toàn phần (σt) được yêu cầu để thu được ước lượng của chỉ số Pp. Trong thực tế,
độ lệch chuẩn toàn phần (σt) được yêu cầu để thu được ước lượng của chỉ số Pp. Trong thực tế, ![]() sẽ là độ lệch chuẩn (St) của toàn bộ dữ liệu. Khi có được giá trị này, chỉ số được ước lượng.
sẽ là độ lệch chuẩn (St) của toàn bộ dữ liệu. Khi có được giá trị này, chỉ số được ước lượng.
5.2.2 Chỉ số Ppk
Khi phân bố của các giá trị cá thể hình thành phân bố chuẩn, trung vị X50 % bằng trung bình (µ). Ngoài ra, X99,865 % - X50 % và X50 % - X0,135 % đều bằng 3 σt. Vì vậy, chỉ số Ppk là giá trị nhỏ hơn trong hai giá trị:
![]()
hoặc
![]()
trong đó Ppk được ước lượng bởi:
![]()
hoặc
![]()
Chỉ số này càng nhỏ thì tỷ lệ cá thể tạo ra nằm ngoài quy định càng cao.
5.3 Chỉ số hiệu năng quá trình đối với dữ liệu đo được (phân bố không chuẩn)
5.3.1 Khái quát
Cách tiếp cận lựa chọn trong điều này đối với dữ liệu không chuẩn giống như đề cập ở 4.5 đối với chỉ số năng lực.
5.3.2 Phương pháp giấy xác suất
Từ biểu đồ tương tự như thể hiện trên Hình 5, có thể thu được ước lượng của các phân vị X0,135 % và X99,865 %. Các ước lượng được ký hiệu tương ứng là Y1 và Y2. công thức trở thành:
![]()
Theo cách tương tự, công thức tính Ppk trở thành:
![]()
hoặc
![]()
chọn biểu thức nào cho giá trị thấp nhất.
Nếu chỉ số nhỏ hơn giá trị đã cho thì quá trình được coi là vượt quá tỷ lệ cá thể nằm ngoài quy định. Tỷ lệ không phù hợp phụ thuộc vào phân bố và giá trị của chỉ số. Liên hệ giữa chỉ số và tỷ lệ cá thể không phù hợp tạo ra phụ thuộc vào lớp phân bố. Cần cẩn trọng để không giải thích các chỉ số trên cơ sở các điểm ngưỡng được rút ra cho phân bố chuẩn và do đó chỉ áp dụng được cho phân bố đó.
Phương pháp giấy xác suất ước lượng trực tiếp các phân vị cực trị và có thể không chính xác. Ngoài ra, phương pháp ước lượng sử dụng giấy xác suất, mặc dù sử dụng rất đơn giản, nhưng hơi thô và quy trình tính toán được ưu tiên (xem Phục lục C).
5.3.3 Phương pháp đường cong Pearson
Đường Pearson chuẩn hóa đôi khi được sử dụng như một lựa chọn thay thế cho giấy xác suất. Phương pháp này được mô tả bằng ví dụ (xem Phụ lực B). Chỉ số được tính toán theo công thức:
![]()
trong đó, ![]() và
và ![]() là phân vị 0,135 % và 99,865 % ước lượng từ đường Pearson chuẩn hóa.
là phân vị 0,135 % và 99,865 % ước lượng từ đường Pearson chuẩn hóa.
Ta cũng có công thức:
![]()
và
![]()
trong đó, ![]() là giá trị trung vị ước lượng.
là giá trị trung vị ước lượng.
Để sử dụng phương pháp này, người sử dụng sẽ cần thiết lập giá trị bất đối xứng và độ nhọn cùng với trung bình và độ lệch chuẩn cho tập dữ liệu dùng để tính toán chỉ số.
Phương pháp này không được ưa dùng nhưng được trình bày ở đây cho hoàn chỉnh vì đôi khi cũng được sử dụng (xem thêm 5.5.3 về việc sử dụng phương pháp này).
5.3.4 Phương pháp xác định phân bố
Xem Phụ lục C về mô tả các họ hàm phân bố nhất định như phân bố loga chuẩn, Rayleigh và Weibull được dùng phổ biến khi nghiên cứu về hiệu năng quá trình. Xem thêm 4.5.4 về việc sử dụng phương pháp này.
5.4 Chỉ số hiệu năng khác đối với dữ liệu đo được
Tất cả các chỉ số cho trước đây đối với năng lực sẽ tương tự như khi xem xét hiệu năng. Độ lệch chuẩn bất kỳ sẽ thể hiện độ biến động tổng thể (σt) thay cho độ biến động vốn có (σ).
5.5 Đánh giá tỷ lệ nằm ngoài quy định đối với phân bố chuẩn của phân bố tổng thể
Ở đây sử dụng phương pháp tương tự như trong 4.8 để ước lượng tỷ lệ nằm ngoài quy định. Người đọc nên thay ![]() và
và ![]() tương ứng cho
tương ứng cho ![]() và
và ![]() . Cũng có thể sử dụng Bảng 3 để xác định tỷ lệ nằm ngoài quy định và người đọc cần nhập
. Cũng có thể sử dụng Bảng 3 để xác định tỷ lệ nằm ngoài quy định và người đọc cần nhập ![]() hoặc
hoặc ![]() vào bảng thay vì
vào bảng thay vì ![]() hoặc
hoặc ![]() .
.
6 Báo cáo chỉ số năng lực và hiệu năng quá trình
Nếu sử dụng các thống kê năng lực (hoặc hiệu năng) quá trình để định lượng quá trình thì chúng phải được báo cáo theo tiêu chuẩn này. Phương pháp tính và số giá trị sử dụng làm cơ sở cho việc tính toán phải được nêu rõ.
Ví dụ được cho trong Bảng 4.
Bảng 4 - Ví dụ về báo cáo chỉ số năng lực quá trình tính được
| Chỉ số năng lực (hoặc hiệu năng) quá trình | Cp = 2,01 |
| Chỉ số năng lực (hoặc hiệu năng) tối thiểu quá trình | Cpk = 1,90 |
| Khoảng tin cậy | 1,54 < Cpk < 2,26 |
| Số giá trị sử dụng cho tính toán | 100 |
| Độ không đảm bảo đo | 0,002 mm |
| Tùy chọn: |
|
| - tần số lấy mẫu; | 30 min. |
| - thời gian và khoảng thời gian lấy dữ liệu; |
|
| - mô hình phân bố; | Chuẩn |
| - điều kiện kỹ thuật (lô, vận hành, công cụ). |
|
Ngoài ra, báo cáo nghiên cứu phải bao gồm thông tin dưới đây:
a) nơi thực hiện nghiên cứu và loại quá trình mà máy là một phần;
b) người thực hiện nghiên cứu và thực hiện phép đo;
c) khi nghiên cứu được thực hiện, bao gồm ngày, giờ bắt đầu và kết thúc, ghi sổ bất kỳ sự gián đoạn nào;
d) số quy chiếu của máy móc và quá trình bất kỳ;
e) tên và số quy chiếu của thành phần;
f) các đặc trưng thành phần đo được;
g) quy định đối với các đặc trưng và những yếu tố nào được giữ không đổi;
h) các điều kiện xung quanh;
i) dữ liệu thô;
j) các điều kiện không chuẩn.
Đối với mỗi đặc trưng đo được, những thông tin dưới đây phải được báo cáo (hoặc cung cấp):
- mô hình phân bố ước lượng được;
- các chỉ số tính được.
Những thông tin dưới đây phải được báo cáo (hoặc cung cấp):
- biểu đồ kiểm soát dữ liệu;
- biểu đồ đối chiếu hoặc biểu đồ tần số của dữ liệu;
- đồ thị xác suất dữ liệu;
- giá trị trung bình từ dữ liệu;
- độ lệch chuẩn từ dữ liệu;
- phần trăm ngoài quy định ước lượng được;
- khoảng tin cậy của chỉ số tính được;
- độ không đảm bảo đo/năng lực quá trình đo.
(tham khảo)
A.1 Khái quát
Cần ước lượng độ lệch chuẩn để tính các chỉ số đề cập trong tiêu chuẩn này. Có hai loại độ lệch chuẩn được xét. Loại thứ nhất được mô tả như độ lệch chuẩn ngắn hạn hoặc độ lệch chuẩn (vốn có) tức thời. Nó thường được tính từ các thống kê lấy từ biểu đồ kiểm soát và điều này được thể hiện trong A.2. Loại thứ hai là ước lượng của độ lệch chuẩn toàn phần và được mô tả trong A.3.
Nếu quá trình có nhiều hơn một phương thức hoặc trạng thái, độ trải cần được tính theo phương pháp dưới đây được cho trong TCVN 9944-2 (ISO 22514-2) hoặc TCVN 9944-8 (ISO 22514-8).
A.2 Độ lệch chuẩn vốn có
A2.1 Ước lượng sử dụng giá trị độ rộng trung bình
Độ lệch chuẩn (quá trình) vốn có (dữ liệu sẽ được lấy từ biểu đồ kiểm soát “được kiểm soát”) có thể được ước lượng từ biểu đồ kiểm soát độ rộng bằng công thức sau đây:
![]()
trong đó d2 là hệ số lấy từ Bảng A.1.
Bảng A1 - Hệ số biểu đồ kiểm soát dùng cho ước lượng độ lệch chuẩn quá trình
| Cỡ nhóm con (n) | d2 | c4 |
| 2 | 1,128 | 0,797 9 |
| 3 | 1,693 | 0,886 2 |
| 4 | 2,059 | 0,921 3 |
| 5 | 2,326 | 0,940 0 |
| 6 | 2,534 | 0,951 5 |
| 7 | 2,704 | 0,959 4 |
| 8 | 2,847 | 0,965 0 |
| 9 | 2,970 | 0,969 3 |
| 10 a | 3,078 | 0,972 7 |
| * Giá trị của d2 và c4 đối với cỡ mẫu lớn hơn 10 có thể tìm trong tài liệu. | ||
A.2.2 Ước lượng sử dụng giá trị độ lệch chuẩn trung bình
Nếu biểu đồ kiểm soát độ lệch chuẩn được sử dụng để theo dõi độ biến động trong nhóm con thì có thể ước lượng độ lệch chuẩn (quá trình) vốn có bằng công thức sau đây:
![]()
trong đó c4 là hệ số biểu đồ kiểm soát lấy từ Bảng A.1.
A.2.3 Ước lượng sử dụng độ lệch chuẩn nhóm con
Nếu độ lệch chuẩn trong nhóm con được tính cho mỗi nhóm con thì có thể ước lượng độ lệch chuẩn (quá trình) vốn có bằng công thức sau đây:

trong đó có m nhóm con, mỗi nhóm gồm n quan trắc.
A.3 Ước lượng độ lệch chuẩn toàn phần
Khi dữ liệu được tạo ra từ quá trình “nằm ngoài kiểm soát” hoặc nếu không sử dụng biểu đồ kiểm soát, thì việc sử dụng các phương pháp của A.2 để tính độ lệch chuẩn là không thích hợp. Thay vào đó nên sử dụng công thức dưới đây:
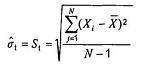
Các trường hợp dẫn đến việc sử dụng công thức này là khi có dao động trong trung bình quá trình do các nguyên nhân ấn định không loại bỏ được gây ra và độ biến động bổ sung này được kết hợp với độ biến động còn lại do nguyên nhân ngẫu nhiên. Đây là thước đo độ biến động thích hợp để sử dụng khi tính các chỉ số hiệu năng.
Khi xét các quá trình nhiều dòng, như ép đúc phun nhiều ngăn, thường cần xử lý dữ liệu từ tất cả các ngăn như chúng thu được từ quá trình đơn lẻ. Dữ liệu từ mỗi ngăn có thể tạo thành một phân bố chuẩn đơn. Tuy nhiên, thực tế thường xảy ra là mỗi ngăn tạo ra phân bố khác biệt đôi chút vì trung bình hoặc độ biến động hoặc cả hai khác nhau. Nếu dữ liệu từ tất cả các dòng quá trình có thể được coi là tạo ra phân bố chuẩn thì công thức này sẽ cho ước lượng độ biến động quá trình tốt nhất.
(tham khảo)
Ước lượng thước đo năng lực và hiệu năng sử dụng đường Pearson - Quy trình và ví dụ 1)
B.1 Ghi chép giới hạn quy định
Giới hạn trên, U = 0,30
Giới hạn dưới, L = 0,20
B.2 Ghi chép thống kê quá trình
Quá trình thể hiện “được kiểm soát” về mặt thống kê
Trung bình, ![]() = 0,235
= 0,235
Độ lệch chuẩn, ![]() = 0,0122
= 0,0122
Độ bất đối xứng, ![]() = 0,7 (làm tròn đến một chữ số thập phân)
= 0,7 (làm tròn đến một chữ số thập phân)
Độ nhọn, ![]() = 3,5 (làm tròn đến một chữ số thập phân)
= 3,5 (làm tròn đến một chữ số thập phân)
B.3 Tra phân vị 0,135 % chuẩn hóa
Đối với bất đối xứng dương, sử dụng Bảng B.1. Đối với bất đối xứng âm, sử dụng Bảng B.2.
Phân vị 0,135, P0,135% = 3,056 nhờ nội suy.
B.4 Tra phân vị 99,865 % chuẩn hóa
Đối với bất đối xứng dương, sử dụng Bảng B.2. Đối với bất đối xứng âm, sử dụng Bảng B.1.
Phân vị 99,865, P99,865% = 4,656 nhờ nội suy.
B.5 Tra trung vị chuẩn hóa trong Bảng B.3
Đối với bất đối xứng dương, đảo dấu. Đối với bất đối xứng âm, để nguyên dương.
Trung vị chuẩn hóa, P50% = - 0,0675 nhờ nội suy.
B.6 Tính ước lượng phân vị 0,135 %
![]()
= 0,235 - (0,012 2 x 3,056)
= 0,197 7
B.7 Tính ước lượng phân vị 99,865 %
![]()
= 0,235 (0,012 2 x 4,656)
= 0,291 8
B.8 Tính ước lượng trung vị
![]()
= 0,235 (0,012 2 x - 0,067 5)
= 0,234 2
B.9 Tính chỉ số năng lực quá trình
![]()
=![]()
= 1,06
![]()
=![]()
= 1,14
![]()
=![]()
= 0,94
Bảng B.1
| Đường Pearson (đuôi chuẩn hóa) P0,135% (phân vị 0,135) đối với γ1 > 0, P99,865% (phân vị 99,865) đối với γ1 < 0 | ||||||||||||||||||||||
| Độ nhọn (β2) | Độ bất đối xứng (γ1) | (β2) | ||||||||||||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 | ||
| -1,4 | 1,512 | 1,421 | 1,317 | 1,206 | 1,092 | 0,979 | 0,868 | 0,762 |
|
|
|
|
|
|
|
|
|
|
|
|
| -1,4 |
| -1,2 | 1,727 | 1,619 | 1,496 | 1,364 | 1,230 | 1,100 | 0,975 | 0,858 | 0,747 |
|
|
|
|
|
|
|
|
|
|
|
| -1,2 |
| -1,0 | 1,966 | 1,840 | 1,696 | 1,541 | 1,384 | 1,232 | 1,089 | 0,957 | 0,836 |
|
|
|
|
|
|
|
|
|
|
|
| -1,0 |
| -0,8 | 2,210 | 2,072 | 1,912 | 1,736 | 1,555 | 1,377 | 1,212 | 1,062 | 0,927 | 0,804 | 0,692 |
|
|
|
|
|
|
|
|
|
| -0,8 |
| -0,6 | 2,442 | 2,298 | 2,129 | 1,941 | 1,740 | 1,539 | 1,348 | 1,175 | 1,023 | 0,887 | 0,766 | 0,656 |
|
|
|
|
|
|
|
|
| -0,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| -0,4 | 2,653 | 2,506 | 2,335 | 2,141 | 1,930 | 1,711 | 1,496 | 1,299 | 1,125 | 0,974 | 0,841 | 0,723 | 0,616 |
|
|
|
|
|
|
|
| -0,4 |
| -0,2 | 2,839 | 2,692 | 2,522 | 2,329 | 2,116 | 1,887 | 1,655 | 1,434 | 1,235 | 1,065 | 0,919 | 0,791 | 0,677 | 0,574 |
|
|
|
|
|
|
| -0,2 |
| 0,0 | 3,000 | 2,856 | 2,689 | 2,500 | 2,289 | 2,059 | 1,817 | 1,578 | 1,356 | 1,1613 | 1,000 | 0,861 | 0,739 | 0,630 | 0,531 |
|
|
|
|
|
| 0,0 |
| 0,2 | 3,140 | 2,986 | 2,834 | 2,653 | 2,447 | 2,220 | 1,976 | 1,726 | 1,485 | 1,269 | 1,086 | 0,933 | 0,801 | 0,686 | 0,583 |
|
|
|
|
|
| 0,2 |
| 0,4 | 3,261 | 3,088 | 2,952 | 2,785 | 2,589 | 2,368 | 2,127 | 1,873 | 1,619 | 1,382 | 1,178 | 1,008 | 0,865 | 0,742 | 0,634 | 0,536 |
|
|
|
|
| 0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,6 | 3,366 | 3,164 | 3,045 | 2,896 | 2,714 | 2,502 | 2,267 | 2,015 | 1,754 | 1,502 | 1,277 | 1,087 | 0,931 | 0,799 | 0,685 | 0,583 | 0,489 |
|
|
|
| 0,6 |
| 0,8 | 3,458 | 3,222 | 3,118 | 2,986 | 2,821 | 2,622 | 2,396 | 2,148 | 1,887 | 1,625 | 1,381 | 1,172 | 1,000 | 0,857 | 0,736 | 0,629 | 0,533 |
|
|
|
| 0,8 |
| 1,0 | 3,539 | 3,266 | 3,174 | 3,058 | 2,910 | 2,727 | 2,512 | 2,271 | 2,013 | 1,748 | 1,491 | 1,262 | 1,072 | 0,917 | 0,787 | 0,675 | 0,575 | 0,484 |
|
|
| 1,0 |
| 1,2 | 3,611 | 3,300 | 3,218 | 3,115 | 2,983 | 2,817 | 2,616 | 2,385 | 2,132 | 1,876 | 1,602 | 1,357 | 1,149 | 0,979 | 0,840 | 0,721 | 0,617 | 0,524 |
|
|
| 1,2 |
| 1,4 | 3,674 | 3,327 | 3,254 | 3,161 | 3,043 | 2,893 | 2,708 | 2,488 | 2,243 | 1,981 | 1,713 | 1,456 | 1,230 | 1,045 | 0,894 | 0,768 | 0,659 | 0,562 | 0,475 |
|
| 1,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1,6 | 3,731 | 3,349 | 3,282 | 3,199 | 3,092 | 2,957 | 2,787 | 2,581 | 2,345 | 2,089 | 1,821 | 1,556 | 1,316 | 1,113 | 0,950 | 0,815 | 0,701 | 0,600 | 0,510 |
|
| 1,6 |
| 1,8 | 3,782 | 3,367 | 3,306 | 3,229 | 3,133 | 3,011 | 2,855 | 2,664 | 2,438 | 2,189 | 1,925 | 1,664 | 1,404 | 1,185 | 1,008 | 0,863 | 0,743 | 0,638 | 0,546 | 0,461 |
| 1,8 |
| 2,0 | 3,828 | 3,382 | 3,325 | 3,255 | 3,167 | 3,055 | 2,914 | 2,736 | 2,524 | 2,283 | 2,023 | 1,755 | 1,494 | 1,261 | 1,068 | 0,913 | 0,785 | 0,676 | 0,580 | 0,494 |
| 2,0 |
| 2,2 | 3,870 | 3,395 | 3,342 | 3,277 | 3,196 | 3,093 | 2,964 | 2,800 | 2,600 | 2,369 | 2,116 | 1,850 | 1,584 | 1,339 | 1,132 | 0,964 | 0,828 | 0,714 | 0,615 | 0,526 | 0,445 | 2,2 |
| 2,4 | 3,908 | 3,405 | 3,356 | 3,295 | 3,220 | 3,126 | 3,006 | 2,855 | 2,669 | 2,448 | 2,202 | 1,940 | 1,673 | 1,420 | 1,198 | 1,018 | 0,873 | 0,752 | 0,649 | 0,557 | 0,475 | 2,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2,6 | 3,943 | 3,415 | 3,367 | 3,311 | 3,241 | 3,153 | 3,043 | 2,904 | 2,730 | 2,521 | 2,283 | 2,026 | 1,760 | 1,501 | 1,267 | 1,073 | 0,918 | 0,791 | 0,683 | 0,589 | 0,504 | 2,6 |
| 2,8 | 3,975 | 3,423 | 3,378 | 3,324 | 3,259 | 3,177 | 3,075 | 2,946 | 2,784 | 2,586 | 2,358 | 2,107 | 1,844 | 1,581 | 1,338 | 1,131 | 0,965 | 0,830 | 0,717 | 0,620 | 0,533 | 2,8 |
| 3,0 | 4,004 | 3,430 | 3,387 | 3,326 | 3,274 | 3,198 | 3,103 | 2,983 | 2,831 | 2,646 | 2,427 | 2,183 | 1,924 | 1,661 | 1,410 | 1,191 | 1,013 | 0,870 | 0,752 | 0,651 | 0,562 | 3,0 |
| 3,2 | 4,031 | 3,436 | 3,395 | 3,346 | 3,288 | 3,216 | 3,127 | 3,015 | 2,874 | 2,699 | 2,491 | 2,254 | 2,000 | 1,738 | 1,483 | 1,253 | 1,063 | 0,911 | 0,787 | 0,681 | 0,590 | 3,2 |
| 3,4 | 4,056 | 3,441 | 3,402 | 3,356 | 3,300 | 3,233 | 3,149 | 3,043 | 2,911 | 2,747 | 2,549 | 2,321 | 2,072 | 1,813 | 1,555 | 1,317 | 1,115 | 0,953 | 0,822 | 0,712 | 0,618 | 3,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 3,6 | 4,079 | 3,446 | 3,408 | 3,364 | 3,311 | 3,247 | 3,168 | 3,069 | 2,945 | 2,790 | 2,602 | 2,383 | 2,140 | 1,884 | 1,626 | 1,381 | 1,169 | 0,996 | 0,858 | 0,744 | 0,646 | 3,6 |
| 3,8 | 4,101 | 3,450 | 3,414 | 3,371 | 3,321 | 3,259 | 3,184 | 3,091 | 2,974 | 2,829 | 2,651 | 2,440 | 2,205 | 1,953 | 1,695 | 1,446 | 1,224 | 1,041 | 0,895 | 0,775 | 0,674 | 3,8 |
| 4,0 | 4,121 | 3,454 | 3,419 | 3,378 | 3,329 | 3,271 | 3,200 | 3,111 | 3,001 | 2,864 | 2,695 | 2,494 | 2,265 | 2,018 | 1,762 | 1,510 | 1,281 | 1,088 | 0,932 | 0,807 | 0,702 | 4,0 |
| 4,2 | 4,140 | 3,458 | 3,423 | 3,384 | 3,337 | 3,281 | 3,213 | 3,129 | 3,025 | 2,895 | 2,735 | 2,543 | 2,321 | 2,080 | 1,827 | 1,574 | 1,338 | 1,135 | 0,971 | 0,839 | 0,730 | 4,2 |
| 4,4 | 4,157 | 3,461 | 3,428 | 3,389 | 3,344 | 3,290 | 3,225 | 3,145 | 3,047 | 2,923 | 2,771 | 2,588 | 2,374 | 2,138 | 1,889 | 1,636 | 1,396 | 1,184 | 1,011 | 0,872 | 0,758 | 4,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4,6 | 4,174 | 3,464 | 3,431 | 3,394 | 3,350 | 3,299 | 3,236 | 3,160 | 3,066 | 2,949 | 2,805 | 2,629 | 2,424 | 2,194 | 1,948 | 1,697 | 1,453 | 1,234 | 1,052 | 0,905 | 0,786 | 4,6 |
| 4,8 | 4,189 | 3,466 | 3,435 | 3,399 | 3,356 | 3,306 | 3,246 | 3,173 | 3,084 | 2,972 | 2,835 | 2,668 | 2,470 | 2,246 | 2,005 | 1,756 | 1,510 | 1,285 | 1,094 | 0,939 | 0,815 | 4,8 |
| 5,0 | 4,204 | 3,469 | 3,438 | 3,403 | 3,362 | 3,313 | 3,256 | 3,186 | 3,100 | 2,994 | 2,863 | 2,703 | 2,513 | 2,296 | 2,059 | 1,813 | 1,566 | 1,336 | 1,137 | 0,975 | 0,844 | 5,0 |
| 5,2 | 4,218 | 3,471 | 3,441 | 3,406 | 3,367 | 3,320 | 3,264 | 3,197 | 3,114 | 3,013 | 2,888 | 2,735 | 2,562 | 2,342 | 2,111 | 1,867 | 1,621 | 1,387 | 1,181 | 1,010 | 0,874 | 5,2 |
| 5,4 | 4,231 | 3,473 | 3,444 | 3,410 | 3,371 | 3,326 | 3,272 | 3,207 | 3,128 | 3,031 | 2,911 | 2,765 | 2,589 | 2,386 | 2,160 | 1,920 | 1,675 | 1,438 | 1,225 | 1,047 | 0,904 | 5,4 |
| 5,6 | 4,243 | 3,475 | 3,446 | 3,413 | 3,375 | 3,331 | 3,279 | 3,216 | 3,140 | 3,047 | 2,933 | 2,793 | 2,624 | 2,427 | 2,206 | 1,970 | 1,727 | 1,489 | 1,270 | 1,085 | 0,935 | 5,6 |
| 5,8 | 4,255 | 3,477 | 3,448 | 3,416 | 3,379 | 3,336 | 3,286 | 3,225 | 3,152 | 3,062 | 2,952 | 2,818 | 2,656 | 2,465 | 2,250 | 2,019 | 1,778 | 1,539 | 1,316 | 1,123 | 0,966 | 5,8 |
| 6,0 | 4,266 | 3,478 | 3,451 | 3,419 | 3,383 | 3,341 | 3,292 | 3,233 | 3,162 | 3,076 | 2,970 | 2,841 | 2,685 | 2,501 | 2,292 | 2,065 | 1,827 | 1,588 | 1,361 | 1,162 | 0,999 | 6,0 |
| 6,2 | 4,276 | 3,480 | 3,453 | 3,422 | 3,386 | 3,345 | 3,297 | 3,240 | 3,172 | 3,089 | 2,987 | 2,863 | 2,713 | 2,535 | 2,332 | 2,109 | 1,874 | 1,635 | 1,407 | 1,202 | 1,031 | 6,2 |
| 6,4 | 4,286 | 3,481 | 3,454 | 3,424 | 3,389 | 3,349 | 3,303 | 3,247 | 3,181 | 3,100 | 3,003 | 2,883 | 2,739 | 2,567 | 2,369 | 2,151 | 1,919 | 1,682 | 1,452 | 1,242 | 1,065 | 6,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 6,6 | 4,296 | 3,483 | 3,456 | 3,426 | 3,392 | 3,353 | 3,308 | 3,254 | 3,189 | 3,111 | 3,017 | 2,902 | 2,763 | 2,597 | 2,405 | 2,191 | 1,962 | 1,727 | 1,496 | 1,282 | 1,099 | 6,6 |
| 6,8 | 4,305 | 3,484 | 3,458 | 3,429 | 3,395 | 3,357 | 3,312 | 3,260 | 3,197 | 3,122 | 3,030 | 2,919 | 2,785 | 2,624 | 2,438 | 2,229 | 2,004 | 1,771 | 1,540 | 1,323 | 1,134 | 6,8 |
| 7,0 | 4,313 | 3,485 | 3,459 | 3,431 | 3,398 | 3,360 | 3,316 | 3,265 | 3,204 | 3,131 | 3,043 | 2,936 | 2,806 | 2,651 | 2,469 | 2,265 | 2,044 | 1,814 | 1,583 | 1,363 | 1,169 | 7,0 |
| 7,2 | 4,322 | 3,486 | 3,461 | 3,432 | 3,400 | 3,363 | 3,321 | 3,270 | 3,211 | 3,140 | 3,054 | 2,951 | 2,825 | 2,675 | 2,499 | 2,300 | 2,083 | 1,855 | 1,625 | 1,403 | 1,204 | 7,2 |
| 7,4 | 4,330 | 3,487 | 3,462 | 3,434 | 3,403 | 3,366 | 3,324 | 3,275 | 3,218 | 3,148 | 3,065 | 2,965 | 2,843 | 2,698 | 2,527 | 2,333 | 2,120 | 1,895 | 1,666 | 1,443 | 1,240 | 7,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 7,6 | 4,337 | 3,488 | 3,464 | 3,436 | 3,405 | 3,369 | 3,328 | 3,280 | 3,224 | 3,156 | 3,075 | 2,978 | 2,860 | 2,720 | 2,554 | 2,364 | 2,155 | 1,933 | 1,706 | 1,482 | 1,276 | 7,6 |
| 7,8 | 4,344 | 3,489 | 3,465 | 3,437 | 3,407 | 3,372 | 3,331 | 3,284 | 3,229 | 3,164 | 3,085 | 2,990 | 2,876 | 2,740 | 2,579 | 2,394 | 2,189 | 1,970 | 1,744 | 1,521 | 1,311 | 7,8 |
| 8,0 | 4,351 | 3,490 | 3,466 | 3,439 | 3,409 | 3,374 | 3,335 | 3,289 | 3,235 | 3,171 | 3,094 | 3,002 | 2,891 | 2,759 | 2,603 | 2,422 | 2,221 | 2,005 | 1,782 | 1,559 | 1,347 | 8,0 |
| 8,2 | 4,358 | 3,491 | 3,467 | 3,440 | 3,411 | 3,377 | 3,338 | 3,292 | 3,240 | 3,177 | 3,103 | 3,013 | 2,906 | 2,777 | 2,625 | 2,449 | 2,252 | 2,040 | 1,818 | 1,596 | 1,382 | 8,2 |
| 8,4 | 4,365 | 3,492 | 3,468 | 3,442 | 3,412 | 3,379 | 3,340 | 3,296 | 3,244 | 3,183 | 3,111 | 3,023 | 2,919 | 2,794 | 2,646 | 2,475 | 2,282 | 2,073 | 1,854 | 1,632 | 1,418 | 8,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 8,6 | 4,371 | 3,492 | 3,469 | 3,443 | 3,414 | 3,381 | 3,343 | 3,300 | 3,249 | 3,189 | 3,118 | 3,033 | 2,932 | 2,810 | 2,666 | 2,499 | 2,310 | 2,104 | 1,888 | 1,667 | 1,452 | 8,6 |
| 8,8 | 4,377 | 3,493 | 3,470 | 3,444 | 3,416 | 3,383 | 3,346 | 3,303 | 3,253 | 3,195 | 3,125 | 3,042 | 2,943 | 2,825 | 2,685 | 2,522 | 2,337 | 2,135 | 1,921 | 1,702 | 1,486 | 8,8 |
| 9,0 | 4,382 | 3,494 | 3,471 | 3,445 | 3,417 | 3,385 | 3,348 | 3,306 | 3,257 | 3,200 | 3,132 | 3,051 | 2,955 | 2,839 | 2,703 | 2,544 | 2,363 | 2,164 | 1,953 | 1,736 | 1,520 | 9,0 |
| 9,2 | 4,388 | 3,495 | 3,472 | 3,447 | 3,418 | 3,387 | 3,351 | 3,309 | 3,261 | 3,205 | 3,138 | 3,059 | 2,965 | 2,853 | 2,720 | 2,565 | 2,388 | 2,192 | 1,984 | 1,768 | 1,553 | 9,2 |
| 9,4 | 4,393 | 3,495 | 3,473 | 3,448 | 3,420 | 3,388 | 3,353 | 3,312 | 3,265 | 3,209 | 3,144 | 3,067 | 2,975 | 2,866 | 2,736 | 2,585 | 2,411 | 2,219 | 2,014 | 1,800 | 1,586 | 9,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 9,6 | 4,398 | 3,496 | 3,473 | 3,449 | 3,421 | 3,390 | 3,355 | 3,315 | 3,268 | 3,214 | 3,150 | 3,075 | 2,985 | 2,878 | 2,752 | 2,604 | 2,434 | 2,245 | 2,042 | 1,831 | 1,617 | 9,6 |
| 9,8 | 4,403 | 3,496 | 4,474 | 3,450 | 3,422 | 3,392 | 3,357 | 3,317 | 3,272 | 3,218 | 3,156 | 3,082 | 2,994 | 2,890 | 2,766 | 2,622 | 2,456 | 2,271 | 2,070 | 1,861 | 1,648 | 9,8 |
| 10,0 | 4,408 | 3,497 | 3,475 | 3,451 | 3,424 | 3,393 | 3,359 | 3,320 | 3,275 | 3,222 | 3,161 | 3,088 | 3,003 | 2,901 | 2,780 | 2,639 | 2,476 | 2,295 | 2,097 | 1,890 | 1,679 | 10,0 |
| 10,2 |
|
|
|
| 3,425 | 3,395 | 3,361 | 3,322 | 3,278 | 3,226 | 3,166 | 3,095 | 3,011 | 2,911 | 2,793 | 2,655 | 2,496 | 2,318 | 2,123 | 1,918 | 1,708 | 10,2 |
| 10,4 |
|
|
|
|
| 3,396 | 3,363 | 3,325 | 3,281 | 3,230 | 3,171 | 3,101 | 3,019 | 2,921 | 2,806 | 2,671 | 2,515 | 2,340 | 2,148 | 1,945 | 1,737 | 10,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 10,6 |
|
|
|
|
|
| 3,364 | 3,327 | 3,283 | 3,233 | 3,175 | 3,107 | 3,026 | 2,930 | 2,818 | 2,686 | 2,533 | 2,361 | 2,172 | 1,972 | 1,765 | 10,6 |
| 10,8 |
|
|
|
|
|
|
| 3,329 | 3,286 | 3,237 | 3,179 | 3,112 | 3,033 | 2,940 | 2,829 | 2,700 | 2,551 | 2,382 | 2,196 | 1,998 | 1,793 | 10,8 |
| 11,0 |
|
|
|
|
|
|
|
| 3,289 | 3,240 | 3,184 | 3,118 | 3,040 | 2,948 | 2,840 | 2,714 | 2,57 | 2,401 | 2,218 | 2,023 | 1,819 | 11,0 |
| 11,2 |
|
|
|
|
|
|
|
|
| 3,243 | 3,188 | 3,123 | 3,046 | 2,956 | 2,851 | 2,727 | 2,583 | 2,420 | 2,240 | 2,047 | 1,845 | 11,2 |
| 11,4 |
|
|
|
|
|
|
|
|
|
| 3,191 | 3,128 | 3,053 | 2,964 | 2,861 | 2,739 | 2,598 | 2,438 | 2,261 | 2,070 | 1,870 | 11,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 11,6 |
|
|
|
|
|
|
|
|
|
| 3,195 | 3,132 | 3,058 | 2,972 | 2,870 | 2,751 | 2,613 | 2,456 | 2,281 | 2,093 | 1,895 | 11,6 |
| 11,8 |
|
|
|
|
|
|
|
|
|
|
| 3,137 | 3,064 | 2,979 | 2,879 | 2,762 | 2,627 | 2,473 | 2,301 | 2,115 | 1,919 | 11,8 |
| 12,0 |
|
|
|
|
|
|
|
|
|
|
| 3,141 | 3,070 | 2,986 | 2,888 | 2,773 | 2,641 | 2,489 | 2,320 | 2,136 | 1,942 | 12,0 |
| 12,2 |
|
|
|
|
|
|
|
|
|
|
|
| 3,075 | 2,993 | 2,896 | 2,784 | 2,653 | 2,505 | 2,338 | 2,157 | 1,965 | 12,2 |
Bảng B.2
| Đường Pearson (đuôi chuẩn hóa) P99,865% (phân vị 99,865) đối với γ1 > 0. P0,135% (phân vị 0,135) đối với γ1 < 0 | ||||||||||||||||||||||
| Độ nhọn (β2) | Độ bất đối xứng (γ1) | (β2) | ||||||||||||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 | ||
| -1,4 | 1,512 | 1,584 | 1,632 | 1,655 | 1,653 | 1,626 | 1,579 | 1,516 |
|
|
|
|
|
|
|
|
|
|
|
|
| -1,4 |
| -1,2 | 1,727 | 1,813 | 1,871 | 1,899 | 1,895 | 1,861 | 1,803 | 1,726 | 1,636 |
|
|
|
|
|
|
|
|
|
|
|
| -1,2 |
| -1,0 | 1,966 | 2,065 | 2,134 | 2,170 | 2,169 | 2,131 | 2,061 | 1,966 | 1,856 |
|
|
|
|
|
|
|
|
|
|
|
| -1,0 |
| -0,8 | 2,210 | 2,320 | 2,400 | 2,446 | 2,454 | 2,422 | 2,349 | 2,241 | 2,108 | 1,965 | 1,822 |
|
|
|
|
|
|
|
|
|
| -0,8 |
| -0,6 | 2,442 | 2,560 | 2,648 | 2,704 | 2,726 | 2,708 | 2,646 | 2,540 | 2,395 | 2,225 | 2,052 | 1,885 |
|
|
|
|
|
|
|
|
| -0,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| -0,4 | 2,653 | 2,774 | 2,869 | 2,934 | 2,969 | 2,968 | 2,926 | 2,837 | 2,699 | 2,518 | 2,314 | 2,114 | 1,928 |
|
|
|
|
|
|
|
| -0,4 |
| -0,2 | 2,839 | 2,961 | 3,060 | 3,133 | 3,179 | 3,194 | 3,173 | 3,109 | 2,993 | 2,824 | 2,608 | 2,373 | 2,152 | 1,952 |
|
|
|
|
|
|
| -0,2 |
| 0,0 | 3,000 | 3,123 | 3,224 | 3,303 | 3,358 | 3,387 | 3,385 | 3,345 | 3,259 | 3,116 | 2,914 | 2,665 | 2,405 | 2,169 | 1,960 |
|
|
|
|
|
| 0,0 |
| 0,2 | 3,140 | 3,261 | 3,364 | 3,447 | 3,510 | 3,550 | 3,564 | 3,546 | 3,488 | 3,378 | 3,206 | 2,970 | 2,690 | 2,412 | 2,167 |
|
|
|
|
|
| 0,2 |
| 0,4 | 3,261 | 3,381 | 3,484 | 3,570 | 3,639 | 3,688 | 3,715 | 3,715 | 3,681 | 3,603 | 3,468 | 3,264 | 2,993 | 2,687 | 2,398 | 2,149 |
|
|
|
|
| 0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,6 | 3,366 | 3,485 | 3,588 | 3,676 | 3,749 | 3,805 | 3,843 | 3,858 | 3,844 | 3,793 | 3,693 | 3,529 | 3,290 | 2,984 | 2,658 | 2,366 | 2,119 |
|
|
|
| 0,6 |
| 0,8 | 3,458 | 3,575 | 3,678 | 3,768 | 3,844 | 3,905 | 3,951 | 3,978 | 3,981 | 3,953 | 3,883 | 3,758 | 3,561 | 3,283 | 2,945 | 2,609 | 2,322 |
|
|
|
| 0,8 |
| 1,0 | 3,539 | 3,654 | 3,757 | 3,847 | 3,926 | 3,991 | 4,044 | 4,080 | 4,096 | 4,087 | 4,043 | 3,952 | 3,797 | 3,561 | 3,243 | 2,881 | 2,547 | 2,269 |
|
|
| 1,0 |
| 1,2 | 3,611 | 3,724 | 3,826 | 3,917 | 3,997 | 4,066 | 4,124 | 4,167 | 4,194 | 4,208 | 4,177 | 4,115 | 3,998 | 3,808 | 3,529 | 3,172 | 2,798 | 2,476 |
|
|
| 1,2 |
| 1,4 | 3,674 | 3,786 | 3,887 | 3,978 | 4,060 | 4,131 | 4,193 | 4,243 | 4,278 | 4,296 | 4,290 | 4,252 | 4,168 | 4,020 | 3,789 | 3,463 | 3,075 | 2,705 | 2,399 |
|
| 1,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1,6 | 3,731 | 3,842 | 3,942 | 4,033 | 4,115 | 4,189 | 4,253 | 4,308 | 4,351 | 4,378 | 4,386 | 4,367 | 4,311 | 4,200 | 4,015 | 3,736 | 3,364 | 2,961 | 2,609 |
|
| 1,6 |
| 1,8 | 3,782 | 3,891 | 3,990 | 4,081 | 4,164 | 4,239 | 4,307 | 4,365 | 4,414 | 4,449 | 4,468 | 4,472 | 4,431 | 4,352 | 4,209 | 3,979 | 3,646 | 3,238 | 2,840 | 2,511 |
| 1,8 |
| 2,0 | 3,828 | 3,936 | 4,034 | 4,125 | 4,208 | 4,285 | 4,354 | 4,416 | 4,468 | 4,511 | 4,539 | 4,549 | 4,532 | 4,479 | 4,372 | 4,189 | 3,907 | 3,522 | 3,095 | 2,719 |
| 2,0 |
| 2,2 | 3,870 | 3,976 | 4,073 | 4,164 | 4,248 | 4,325 | 4,396 | 4,460 | 4,517 | 4,564 | 4,600 | 4,620 | 4,619 | 4,587 | 4,510 | 4,369 | 4,137 | 3,796 | 3,370 | 2,949 | 2,603 | 2,2 |
| 2,4 | 3,908 | 4,013 | 4,109 | 4,199 | 4,283 | 4,361 | 4,433 | 4,500 | 4,559 | 4,611 | 4,653 | 4,682 | 4,693 | 4,678 | 4,627 | 4,521 | 4,336 | 4,047 | 3,648 | 3,201 | 2,808 | 2,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2,6 | 3,943 | 4,046 | 4,142 | 4,231 | 4,315 | 4,394 | 4,467 | 4,535 | 4,597 | 4,653 | 4,700 | 4,736 | 4,757 | 4,756 | 4,725 | 4,649 | 4,506 | 4,269 | 3,916 | 3,471 | 3,033 | 2,6 |
| 2,8 | 3,975 | 4,077 | 4,172 | 4,261 | 4,344 | 4,423 | 4,498 | 4,567 | 4,631 | 4,690 | 4,741 | 4,783 | 4,812 | 4,824 | 4,809 | 4,758 | 4,650 | 4,460 | 4,160 | 3,745 | 3,280 | 2,8 |
| 3,0 | 4,004 | 4,105 | 4,199 | 4,287 | 4,371 | 4,450 | 4,525 | 4,596 | 4,662 | 4,723 | 4,777 | 4,824 | 4,860 | 4,882 | 4,881 | 4,850 | 4,771 | 4,623 | 4,376 | 4,007 | 3,544 | 3,0 |
| 3,2 | 4,031 | 4,131 | 4,224 | 4,312 | 4,396 | 4,475 | 4,550 | 4,622 | 4,689 | 4,752 | 4,810 | 4,861 | 4,903 | 4,932 | 4,944 | 4,929 | 4,875 | 4,762 | 4,563 | 4,247 | 3,813 | 3,2 |
| 3,4 | 4,056 | 4,155 | 4,247 | 4,335 | 4,418 | 4,498 | 4,573 | 4,645 | 4,714 | 4,779 | 4,839 | 4,893 | 4,940 | 4,976 | 4,997 | 4,996 | 4,963 | 4,880 | 4,723 | 4,461 | 4,072 | 3,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 3,6 | 4,079 | 4,177 | 4,269 | 4,356 | 4,439 | 4,518 | 4,594 | 4,667 | 4,737 | 4,803 | 4,865 | 4,922 | 4,973 | 5,015 | 5,044 | 5,055 | 5,038 | 4,980 | 4,859 | 4,647 | 4,311 | 3,6 |
| 3,8 | 4,101 | 4,197 | 4,288 | 4,375 | 4,458 | 4,537 | 4,614 | 4,687 | 4,757 | 4,825 | 4,888 | 4,948 | 5,002 | 5,049 | 5,085 | 5,106 | 5,103 | 5,066 | 4,976 | 4,806 | 4,524 | 3,8 |
| 4,0 | 4,121 | 4,217 | 4,307 | 4,393 | 4,476 | 4,555 | 4,631 | 4,705 | 4,776 | 4,845 | 4,910 | 4,972 | 5,029 | 5,080 | 5,122 | 5,150 | 5,159 | 5,139 | 5,075 | 4,943 | 4,712 | 4,0 |
| 4,2 | 4,140 | 4,234 | 4,324 | 4,410 | 4,492 | 4,571 | 4,648 | 4,722 | 4,794 | 4,863 | 4,929 | 4,993 | 5,052 | 5,107 | 5,153 | 5,189 | 5,208 | 5,202 | 5,519 | 5,509 | 4,873 | 4,2 |
| 4,4 | 4,157 | 4,251 | 4,340 | 4,425 | 4,508 | 4,587 | 4,663 | 4,737 | 4,809 | 4,879 | 4,947 | 5,012 | 5,074 | 5,131 | 5,181 | 5,223 | 5,250 | 5,257 | 5,232 | 5,159 | 5,012 | 4,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4,6 | 4,174 | 4,267 | 4,355 | 4,440 | 4,522 | 4,601 | 4,677 | 4,752 | 4,824 | 4,895 | 4,963 | 5,029 | 5,093 | 5,152 | 5,207 | 5,253 | 5,288 | 5,305 | 5,295 | 5,244 | 5,131 | 4,6 |
| 4,8 | 4,189 | 4,281 | 4,369 | 4,454 | 4,535 | 4,614 | 4,691 | 4,765 | 4,838 | 4,909 | 4,978 | 5,045 | 5,110 | 5,172 | 5,229 | 5,280 | 5,321 | 5,346 | 5,349 | 5,318 | 5,233 | 4,8 |
| 5,0 | 4,204 | 4,295 | 4,383 | 4,467 | 4,548 | 4,627 | 4,703 | 4,778 | 4,851 | 4,922 | 4,992 | 5,060 | 5,126 | 5,190 | 5,249 | 5,303 | 5,350 | 5,383 | 5,396 | 5,381 | 5,320 | 5,0 |
| 5,2 | 4,218 | 4,308 | 4,395 | 4,479 | 4,560 | 4,638 | 4,715 | 4,789 | 4,862 | 4,934 | 5,004 | 5,073 | 5,141 | 5,206 | 5,267 | 5,325 | 5,376 | 5,415 | 5,437 | 5,436 | 5,395 | 5,2 |
| 5,4 | 4,231 | 4,321 | 4,407 | 4,490 | 4,571 | 4,649 | 4,725 | 4,800 | 4,873 | 4,945 | 5,016 | 5,086 | 5,154 | 5,220 | 5,284 | 5,344 | 5,399 | 5,443 | 5,474 | 5,483 | 5,460 | 5,4 |
| 5,6 | 4,243 | 4,332 | 4,418 | 4,501 | 4,581 | 4,659 | 4,736 | 4,810 | 4,884 | 4,956 | 5,027 | 5,097 | 5,166 | 5,233 | 5,299 | 5,361 | 5,418 | 5,468 | 5,505 | 5,525 | 5,516 | 5,6 |
| 5,8 | 4,255 | 4,343 | 4,429 | 4,511 | 4,591 | 4,669 | 4,745 | 4,820 | 4,893 | 4,966 | 5,037 | 5,108 | 5,177 | 5,246 | 5,312 | 5,376 | 5,436 | 5,491 | 5,533 | 5,561 | 5,565 | 5,8 |
| 6,0 | 4,266 | 4,354 | 4,439 | 4,521 | 4,600 | 4,678 | 4,754 | 4,829 | 4,902 | 4,975 | 5,046 | 5,117 | 5,188 | 5,257 | 5,325 | 5,390 | 5,452 | 5,511 | 5,558 | 5,593 | 5,608 | 6,0 |
| 6,2 | 4,276 | 4,364 | 4,448 | 4,530 | 4,609 | 4,695 | 4,763 | 4,837 | 4,911 | 4,983 | 5,055 | 5,126 | 5,197 | 5,267 | 5,336 | 5,403 | 5,467 | 5,529 | 5,581 | 5,621 | 5,645 | 6,2 |
| 6,4 | 4,286 | 4,373 | 4,457 | 4,538 | 4,618 | 4,703 | 4,771 | 4,845 | 4,919 | 4,991 | 5,063 | 5,135 | 5,206 | 5,276 | 5,346 | 5,414 | 5,480 | 5,542 | 5,600 | 5,646 | 5,678 | 6,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 6,6 | 4,296 | 4,382 | 4,466 | 4,547 | 4,626 | 4,710 | 4,778 | 4,853 | 4,926 | 4,999 | 5,071 | 5,143 | 5,214 | 5,285 | 5,356 | 5,425 | 5,492 | 5,557 | 5,618 | 5,669 | 5,706 | 6,6 |
| 6,8 | 4,305 | 4,391 | 4,474 | 4,554 | 4,633 | 4,717 | 4,785 | 4,860 | 4,933 | 5,006 | 5,078 | 5,150 | 5,222 | 5,293 | 5,364 | 5,434 | 5,503 | 5,569 | 5,634 | 5,688 | 5,732 | 6,8 |
| 7,0 | 4,313 | 4,399 | 4,481 | 4,562 | 4,640 | 4,724 | 4,792 | 4,867 | 4,940 | 5,013 | 5,085 | 5,157 | 5,229 | 5,301 | 5,372 | 5,443 | 5,513 | 5,581 | 5,648 | 5,706 | 5,754 | 7,0 |
| 7,2 | 4,322 | 4,406 | 4,489 | 4,569 | 4,647 | 4,730 | 4,799 | 4,873 | 4,946 | 5,019 | 5,091 | 5,164 | 5,236 | 5,308 | 5,380 | 5,451 | 5,522 | 5,591 | 5,658 | 5,722 | 5,775 | 7,2 |
| 7,4 | 4,330 | 4,414 | 4,496 | 4,576 | 4,654 | 4,736 | 4,805 | 4,879 | 4,952 | 5,025 | 5,097 | 5,170 | 5,242 | 5,314 | 5,387 | 5,459 | 5,530 | 5,601 | 5,669 | 5,736 | 5,792 | 7,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 7,6 | 4,337 | 4,421 | 4,503 | 4,582 | 4,660 | 4,742 | 4,811 | 4,885 | 4,958 | 5,031 | 5,103 | 5,175 | 5,248 | 5,320 | 5,393 | 5,466 | 5,538 | 5,609 | 5,679 | 5,749 | 5,808 | 7,6 |
| 7,8 | 4,344 | 4,428 | 4,509 | 4,588 | 4,666 | 4,747 | 4,817 | 4,890 | 4,963 | 5,036 | 5,109 | 5,181 | 5,253 | 5,326 | 5,399 | 5,472 | 5,545 | 5,617 | 5,688 | 5,760 | 5,823 | 7,8 |
| 8,0 | 4,351 | 4,434 | 4,515 | 4,594 | 4,672 | 4,753 | 4,822 | 4,896 | 4,969 | 5,041 | 5,114 | 5,186 | 5,259 | 5,331 | 5,404 | 5,478 | 5,551 | 5,624 | 5,696 | 5,771 | 5,836 | 8,0 |
| 8,2 | 4,358 | 4,441 | 4,521 | 4,600 | 4,677 | 4,758 | 4,827 | 4,901 | 4,974 | 5,046 | 5,118 | 5,191 | 5,263 | 5,336 | 5,410 | 5,483 | 5,557 | 5,631 | 5,704 | 5,775 | 5,847 | 8,2 |
| 8,4 | 4,365 | 4,447 | 4,527 | 4,605 | 4,682 | 4,762 | 4,832 | 4,905 | 4,978 | 5,051 | 5,123 | 5,195 | 5,268 | 5,341 | 5,414 | 5,488 | 5,562 | 5,637 | 5,710 | 5,783 | 5,858 | 8,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 8,6 | 4,371 | 4,452 | 4,532 | 4,611 | 4,687 | 4,767 | 4,837 | 4,910 | 4,983 | 5,055 | 5,127 | 5,200 | 5,272 | 5,345 | 5,419 | 5,493 | 5,567 | 5,642 | 5,717 | 5,790 | 5,867 | 8,6 |
| 8,8 | 4,377 | 4,458 | 4,538 | 4,616 | 4,692 | 4,772 | 4,841 | 4,914 | 4,987 | 5,059 | 5,132 | 5,204 | 5,276 | 5,349 | 5,423 | 5,497 | 5,572 | 5,647 | 5,722 | 5,797 | 5,875 | 8,8 |
| 9,0 | 4,382 | 4,463 | 4,543 | 4,621 | 4,697 | 4,776 | 4,845 | 4,918 | 4,991 | 5,063 | 5,135 | 5,208 | 5,280 | 5,353 | 5,427 | 5,501 | 5,576 | 5,652 | 5,727 | 5,803 | 5,883 | 9,0 |
| 9,2 | 4,388 | 4,468 | 4,548 | 4,625 | 4,701 | 4,780 | 4,850 | 4,923 | 4,995 | 5,067 | 5,139 | 5,211 | 5,284 | 5,357 | 5,431 | 5,505 | 5,580 | 5,656 | 5,732 | 5,808 | 5,883 | 9,2 |
| 9,4 | 4,393 | 4,473 | 4,552 | 4,630 | 4,705 | 4,784 | 4,854 | 4,926 | 4,999 | 5,071 | 5,143 | 5,215 | 5,287 | 5,361 | 5,434 | 5,509 | 5,584 | 5,660 | 5,736 | 5,813 | 5,889 | 9,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 9,6 | 4,398 | 4,478 | 4,557 | 4,634 | 4,710 | 4,788 | 4,8574 | 4,930 | 5,002 | 5,074 | 5,146 | 5,218 | 5,291 | 5,364 | 5,437 | 5,512 | 5,587 | 5,663 | 5,740 | 5,817 | 5,894 | 9,6 |
| 9,8 | 4,403 | 4,483 | 4,561 | 4,638 | 4,714 | 4,791 | 4,861 | 4,934 | 5,006 | 5,078 | 5,149 | 5,222 | 5,294 | 5,367 | 5,440 | 5,515 | 5,590 | 5,667 | 5,744 | 5,821 | 5,898 | 9,8 |
| 10,0 | 4,408 | 4,487 | 4,565 | 4,642 | 4,717 | 4,795 | 4,865 | 4,937 | 5,009 | 5,081 | 5,153 | 5,225 | 5,297 | 5,370 | 5,443 | 5,518 | 5,593 | 5,670 | 5,747 | 5,825 | 5,903 | 10,0 |
| 10,2 |
|
|
|
| 4,721 | 4,798 | 4,868 | 4,940 | 5,012 | 5,084 | 5,156 | 5,228 | 5,300 | 5,373 | 5,446 | 5,521 | 5,596 | 5,673 | 5,750 | 5,828 | 5,906 | 10,2 |
| 10,4 |
|
|
|
|
|
| 4,871 | 4,943 | 5,015 | 5,087 | 5,158 | 5,230 | 5,303 | 5,375 | 5,449 | 5,523 | 5,599 | 5,675 | 5,753 | 5,831 | 5,910 | 10,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 10,6 |
|
|
|
|
|
| 4,874 | 4,947 | 5,018 | 5,090 | 5,161 | 5,233 | 5,305 | 5,378 | 5,451 | 5,526 | 5,601 | 5,678 | 5,755 | 5,834 | 5,913 | 10,6 |
| 10,8 |
|
|
|
|
|
|
| 4,949 | 5,021 | 5,092 | 5,164 | 5,236 | 5,308 | 5,380 | 5,454 | 5,528 | 5,603 | 5,680 | 5,757 | 5,836 | 5,915 | 10,8 |
| 11,0 |
|
|
|
|
|
|
|
| 5,024 | 5,095 | 5,166 | 5,238 | 5,310 | 5,383 | 5,456 | 5,530 | 5,605 | 5,682 | 5,760 | 5,838 | 5,918 | 11,0 |
| 11,2 |
|
|
|
|
|
|
|
|
| 5,098 | 5,169 | 5,240 | 5,312 | 5,385 | 5,458 | 5,532 | 5,607 | 5,684 | 5,762 | 5,840 | 5,920 | 11,2 |
| 11,4 |
|
|
|
|
|
|
|
|
|
| 5,171 | 5,243 | 5,314 | 5,387 | 5,460 | 5,534 | 5,609 | 5,686 | 5,763 | 5,842 | 5,922 | 11,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 11,6 |
|
|
|
|
|
|
|
|
|
| 5,173 | 5,245 | 5,316 | 5,389 | 5,462 | 5,536 | 5,611 | 5,687 | 5,765 | 5,844 | 5,924 | 11,6 |
| 11,8 |
|
|
|
|
|
|
|
|
|
|
| 5,247 | 5,318 | 5,391 | 5,464 | 5,538 | 5,613 | 5,689 | 5,767 | 5,845 | 5,925 | 11,8 |
| 12,0 |
|
|
|
|
|
|
|
|
|
|
| 5,249 | 5,320 | 5,393 | 5,465 | 5,539 | 5,614 | 5,690 | 5,768 | 5,847 | 5,927 | 12,0 |
| 12,2 |
|
|
|
|
|
|
|
|
|
|
|
| 5,322 | 5,394 | 5,467 | 5,541 | 5,616 | 5,692 | 5,769 | 5,848 | 5,928 | 12,2 |
Bảng B.3
| Đường Pearson (trung vị chuẩn hóa) P50% (phân vị 50). Đổi dấu đối với γ1 > 0 | ||||||||||||||||||||||
| Độ nhọn (β2) | Độ bất đối xứng (γ1) | (β2) | ||||||||||||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 | ||
| -1,4 | 0,000 | 0,053 | 0,111 | 0,184 | 0,282 | 0,424 | 0,0627 | 0,754 |
|
|
|
|
|
|
|
|
|
|
|
|
| -1,4 |
| -1,2 | 0,000 | 0,039 | 0,082 | 0,132 | 0,196 | 0,284 | 0,412 | 0,591 | 0,727 |
|
|
|
|
|
|
|
|
|
|
|
| -1,2 |
| -1,0 | 0,000 | 0,031 | 0,065 | 0,103 | 0,151 | 0,212 | 0,297 | 0,419 | 0,586 |
|
|
|
|
|
|
|
|
|
|
|
| -1,0 |
| -0,8 | 0,000 | 0,026 | 0,054 | 0,085 | 0,123 | 0,169 | 0,231 | 0,317 | 0,439 | 0,598 | 0,681 |
|
|
|
|
|
|
|
|
|
| -0,8 |
| -0,6 | 0,000 | 0,023 | 0,047 | 0,073 | 0,104 | 0,142 | 0,190 | 0,254 | 0,343 | 0,468 | 0,616 | 0,653 |
|
|
|
|
|
|
|
|
| -0,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| -0,4 | 0,000 | 0,020 | 0,041 | 0,064 | 0,091 | 0,122 | 0,161 | 0,212 | 0,280 | 0,375 | 0,504 | 0,633 | 0,616 |
|
|
|
|
|
|
|
| -0,4 |
| -0,2 | 0,000 | 0,018 | 0,037 | 0,058 | 0,081 | 0,108 | 0,141 | 0,183 | 0,237 | 0,311 | 0,413 | 0,542 | 0,638 | 0,574 |
|
|
|
|
|
|
| -0,2 |
| 0,0 | 0,000 | 0,017 | 0,034 | 0,053 | 0,073 | 0,097 | 0,126 | 0,161 | 0,206 | 0,266 | 0,347 | 0,456 | 0,579 | 0,621 | 0,531 |
|
|
|
|
|
| 0,0 |
| 0,2 | 0,000 | 0,015 | 0,032 | 0,049 | 0,068 | 0,089 | 0,114 | 0,145 | 0,183 | 0,233 | 0,299 | 0,388 | 0,501 | 0,605 | 0,582 |
|
|
|
|
|
| 0,2 |
| 0,4 | 0,000 | 0,014 | 0,029 | 0,045 | 0,063 | 0,082 | 0,105 | 0,132 | 0,165 | 0,208 | 0,263 | 0,336 | 0,433 | 0,545 | 0,607 | 0,536 |
|
|
|
|
| 0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,6 | 0,000 | 0,013 | 0,028 | 0,043 | 0,059 | 0,077 | 0,097 | 0,122 | 0,151 | 0,188 | 0,235 | 0,297 | 0,379 | 0,481 | 0,579 | 0,579 | 0,489 |
|
|
|
| 0,6 |
| 0,8 | 0,000 | 0,013 | 0,026 | 0,040 | 0,055 | 0,072 | 0,091 | 0,113 | 0,140 | 0,172 | 0,213 | 0,266 | 0,336 | 0,425 | 0,527 | 0,590 | 0,533 |
|
|
|
| 0,8 |
| 1,0 | 0,000 | 0,012 | 0,025 | 0,038 | 0,053 | 0,068 | 0,086 | 0,106 | 0,130 | 0,159 | 0,196 | 0,242 | 0,301 | 0,379 | 0,474 | 0,563 | 0,569 | 0,484 |
|
|
| 1,0 |
| 1,2 | 0,000 | 0,011 | 0,024 | 0,036 | 0,050 | 0,065 | 0,082 | 0,100 | 0,122 | 0,148 | 0,181 | 0,222 | 0,274 | 0,341 | 0,426 | 0,520 | 0,576 | 0,524 |
|
|
| 1,2 |
| 1,4 | 0,000 | 0,011 | 0,023 | 0,035 | 0,048 | 0,062 | 0,078 | 0,095 | 0,116 | 0,140 | 0,169 | 0,206 | 0,252 | 0,310 | 0,385 | 0,474 | 0,554 | 0,555 | 0,475 |
|
| 1,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1,6 | 0,000 | 0,010 | 0,022 | 0,034 | 0,046 | 0,060 | 0,074 | 0,091 | 0,110 | 0,132 | 0,159 | 0,192 | 0,233 | 0,285 | 0,351 | 0,432 | 0,518 | 0,564 | 0,510 |
|
| 1,6 |
| 1,8 | 0,000 | 0,010 | 0,021 | 0,032 | 0,044 | 0,057 | 0,072 | 0,087 | 0,105 | 0,126 | 0,151 | 0,180 | 0,217 | 0,264 | 0,323 | 0,396 | 0,480 | 0,549 | 0,540 | 0,461 |
| 1,8 |
| 2,0 | 0,000 | 0,009 | 0,020 | 0,031 | 0,043 | 0,055 | 0,069 | 0,084 | 0,101 | 0,120 | 0,143 | 0,171 | 0,204 | 0,246 | 0,299 | 0,365 | 0,443 | 0,521 | 0,552 | 0,494 |
| 2,0 |
| 2,2 | 0,000 | 0,009 | 0,020 | 0,030 | 0,042 | 0,054 | 0,067 | 0,081 | 0,097 | 0,115 | 0,137 | 0,162 | 0,193 | 0,231 | 0,279 | 0,338 | 0,410 | 0,488 | 0,544 | 0,522 | 0,445 | 2,2 |
| 2,4 | 0,000 | 0,009 | 0,019 | 0,029 | 0,040 | 0,052 | 0,065 | 0,078 | 0,094 | 0,111 | 0,131 | 0,155 | 0,183 | 0,218 | 0,261 | 0,315 | 0,381 | 0,456 | 0,524 | 0,538 | 0,475 | 2,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2,6 | 0,000 | 0,008 | 0,018 | 0,029 | 0,039 | 0,051 | 0,063 | 0,076 | 0,091 | 0,107 | 0,126 | 0,148 | 0,175 | 0,207 | 0,246 | 0,295 | 0,355 | 0,426 | 0,498 | 0,539 | 0,503 | 2,6 |
| 2,8 | 0,000 | 0,008 | 0,018 | 0,028 | 0,038 | 0,049 | 0,061 | 0,074 | 0,088 | 0,104 | 0,122 | 0,143 | 0,167 | 0,197 | 0,233 | 0,278 | 0,333 | 0,398 | 0,470 | 0,526 | 0,522 | 2,8 |
| 3,0 | 0,000 | 0,008 | 0,017 | 0,027 | 0,037 | 0,048 | 0,059 | 0,072 | 0,085 | 0,101 | 0,118 | 0,138 | 0,161 | 0,189 | 0,222 | 0,263 | 0,313 | 0,374 | 0,443 | 0,506 | 0,530 | 3,0 |
| 3,2 | 0,000 | 0,008 | 0,017 | 0,027 | 0,037 | 0,047 | 0,058 | 0,070 | 0,083 | 0,098 | 0,114 | 0,133 | 0,155 | 0,181 | 0,212 | 0,250 | 0,296 | 0,352 | 0,417 | 0,483 | 0,525 | 3,2 |
| 3,4 | 0,000 | 0,008 | 0,017 | 0,026 | 0,036 | 0,046 | 0,057 | 0,068 | 0,081 | 0,095 | 0,111 | 0,129 | 0,150 | 0,174 | 0,203 | 0,239 | 0,281 | 0,333 | 0,394 | 0,460 | 0,513 | 3,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 3,6 | 0,000 | 0,007 | 0,016 | 0,025 | 0,035 | 0,045 | 0,056 | 0,067 | 0,079 | 0,093 | 0,108 | 0,125 | 0,145 | 0,168 | 0,196 | 0,228 | 0,268 | 0,316 | 0,373 | 0,437 | 0,495 | 3,6 |
| 3,8 | 0,000 | 0,007 | 0,016 | 0,025 | 0,034 | 0,044 | 0,054 | 0,066 | 0,078 | 0,091 | 0,105 | 0,122 | 0,141 | 0,163 | 0,188 | 0,219 | 0,256 | 0,301 | 0,354 | 0,415 | 0,475 | 3,8 |
| 4,0 | 0,000 | 0,007 | 0,015 | 0,025 | 0,034 | 0,043 | 0,053 | 0,064 | 0,076 | 0,089 | 0,103 | 0,119 | 0,137 | 0,158 | 0,182 | 0,211 | 0,246 | 0,288 | 0,337 | 0,395 | 0,455 | 4,0 |
| 4,2 | 0,000 | 0,007 | 0,015 | 0,024 | 0,033 | 0,043 | 0,053 | 0,063 | 0,075 | 0,087 | 0,101 | 0,116 | 0,133 | 0,153 | 0,176 | 0,204 | 0,236 | 0,276 | 0,322 | 0,376 | 0,435 | 4,2 |
| 4,4 | 0,000 | 0,007 | 0,015 | 0,024 | 0,033 | 0,042 | 0,052 | 0,062 | 0,073 | 0,085 | 0,099 | 0,113 | 0,130 | 0,149 | 0,171 | 0,197 | 0,228 | 0,265 | 0,308 | 0,359 | 0,416 | 4,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4,6 | 0,000 | 0,007 | 0,015 | 0,023 | 0,032 | 0,041 | 0,051 | 0,061 | 0,072 | 0,084 | 0,097 | 0,111 | 0,127 | 0,145 | 0,167 | 0,191 | 0,220 | 0,255 | 0,296 | 0,344 | 0,399 | 4,6 |
| 4,8 | 0,000 | 0,006 | 0,015 | 0,023 | 0,032 | 0,041 | 0,050 | 0,060 | 0,071 | 0,082 | 0,095 | 0,109 | 0,124 | 0,142 | 0,162 | 0,186 | 0,213 | 0,246 | 0,285 | 0,330 | 0,382 | 4,8 |
| 5,0 | 0,000 | 0,006 | 0,014 | 0,023 | 0,031 | 0,040 | 0,049 | 0,059 | 0,070 | 0,081 | 0,093 | 0,107 | 0,122 | 0,139 | 0,158 | 0,181 | 0,207 | 0,238 | 0,274 | 0,317 | 0,367 | 5,0 |
| 5,2 | 0,000 | 0,006 | 0,014 | 0,022 | 0,031 | 0,040 | 0,049 | 0,058 | 0,069 | 0,080 | 0,092 | 0,105 | 0,119 | 0,136 | 0,155 | 0,176 | 0,201 | 0,231 | 0,265 | 0,306 | 0,353 | 5,2 |
| 5,4 | 0,000 | 0,006 | 0,014 | 0,022 | 0,030 | 0,039 | 0,048 | 0,057 | 0,068 | 0,078 | 0,090 | 0,103 | 0,117 | 0,133 | 0,151 | 0,172 | 0,196 | 0,224 | 0,257 | 0,295 | 0,340 | 5,4 |
| 5,6 | 0,000 | 0,006 | 0,014 | 0,022 | 0,030 | 0,039 | 0,047 | 0,057 | 0,067 | 0,077 | 0,089 | 0,101 | 0,115 | 0,131 | 0,148 | 0,168 | 0,191 | 0,218 | 0,249 | 0,285 | 0,328 | 5,6 |
| 5,8 | 0,000 | 0,006 | 0,014 | 0,022 | 0,030 | 0,038 | 0,047 | 0,056 | 0,066 | 0,076 | 0,087 | 0,100 | 0,113 | 0,128 | 0,145 | 0,164 | 0,186 | 0,212 | 0,242 | 0,277 | 0,317 | 5,8 |
| 6,0 | 0,000 | 0,006 | 0,014 | 0,021 | 0,029 | 0,038 | 0,046 | 0,055 | 0,065 | 0,075 | 0,086 | 0,098 | 0,111 | 0,126 | 0,142 | 0,161 | 0,182 | 0,207 | 0,235 | 0,268 | 0,307 | 6,0 |
| 6,2 | 0,000 | 0,006 | 0,013 | 0,021 | 0,029 | 0,037 | 0,046 | 0,055 | 0,064 | 0,074 | 0,085 | 0,097 | 0,110 | 0,124 | 0,140 | 0,158 | 0,178 | 0,202 | 0,229 | 0,261 | 0,298 | 6,2 |
| 6,4 | 0,000 | 0,006 | 0,013 | 0,021 | 0,029 | 0,037 | 0,045 | 0,054 | 0,063 | 0,073 | 0,084 | 0,096 | 0,108 | 0,122 | 0,137 | 0,155 | 0,175 | 0,197 | 0,223 | 0,254 | 0,289 | 6,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 6,6 | 0,000 | 0,006 | 0,013 | 0,021 | 0,028 | 0,037 | 0,045 | 0,054 | 0,063 | 0,073 | 0,083 | 0,094 | 0,107 | 0,120 | 0,135 | 0,152 | 0,171 | 0,193 | 0,218 | 0,247 | 0,281 | 6,6 |
| 6,8 | 0,000 | 0,006 | 0,013 | 0,021 | 0,028 | 0,036 | 0,044 | 0,053 | 0,062 | 0,072 | 0,082 | 0,093 | 0,105 | 0,118 | 0,133 | 0,150 | 0,168 | 0,189 | 0,213 | 0,241 | 0,273 | 6,8 |
| 7,0 | 0,000 | 0,005 | 0,013 | 0,020 | 0,028 | 0,036 | 0,044 | 0,053 | 0,061 | 0,071 | 0,081 | 0,092 | 0,104 | 0,117 | 0,131 | 0,147 | 0,165 | 0,185 | 0,209 | 0,236 | 0,267 | 7,0 |
| 7,2 | 0,000 | 0,005 | 0,013 | 0,020 | 0,028 | 0,036 | 0,044 | 0,052 | 0,061 | 0,070 | 0,080 | 0,091 | 0,103 | 0,115 | 0,129 | 0,145 | 0,162 | 0,182 | 0,205 | 0,230 | 0,260 | 7,2 |
| 7,4 | 0,000 | 0,005 | 0,013 | 0,020 | 0,027 | 0,035 | 0,043 | 0,052 | 0,060 | 0,070 | 0,079 | 0,090 | 0,101 | 0,114 | 0,128 | 0,143 | 0,160 | 0,179 | 0,201 | 0,226 | 0,254 | 7,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 7,6 | 0,000 | 0,005 | 0,012 | 0,020 | 0,027 | 0,035 | 0,043 | 0,051 | 0,060 | 0,069 | 0,079 | 0,089 | 0,100 | 0,113 | 0,126 | 0,141 | 0,157 | 0,176 | 0,197 | 0,221 | 0,249 | 7,6 |
| 7,8 | 0,000 | 0,005 | 0,012 | 0,020 | 0,027 | 0,035 | 0,043 | 0,051 | 0,059 | 0,068 | 0,078 | 0,088 | 0,099 | 0,111 | 0,124 | 0,139 | 0,155 | 0,173 | 0,193 | 0,217 | 0,243 | 7,8 |
| 8,0 | 0,000 | 0,005 | 0,012 | 0,019 | 0,027 | 0,034 | 0,042 | 0,050 | 0,059 | 0,068 | 0,077 | 0,087 | 0,098 | 0,110 | 0,123 | 0,137 | 0,153 | 0,170 | 0,190 | 0,213 | 0,238 | 8,0 |
| 8,2 | 0,000 | 0,005 | 0,012 | 0,019 | 0,027 | 0,034 | 0,042 | 0,050 | 0,058 | 0,067 | 0,076 | 0,086 | 0,097 | 0,109 | 0,121 | 0,135 | 0,151 | 0,168 | 0,187 | 0,209 | 0,234 | 8,2 |
| 8,4 | 0,000 | 0,005 | 0,012 | 0,019 | 0,026 | 0,034 | 0,042 | 0,050 | 0,058 | 0,067 | 0,076 | 0,086 | 0,096 | 0,108 | 0,120 | 0,134 | 0,149 | 0,165 | 0,184 | 0,205 | 0,229 | 8,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 8,6 | 0,000 | 0,005 | 0,012 | 0,019 | 0,026 | 0,034 | 0,041 | 0,049 | 0,057 | 0,066 | 0,075 | 0,085 | 0,095 | 0,107 | 0,119 | 0,132 | 0,147 | 0,163 | 0,181 | 0,202 | 0,225 | 8,6 |
| 8,8 | 0,000 | 0,005 | 0,012 | 0,019 | 0,026 | 0,033 | 0,041 | 0,049 | 0,057 | 0,066 | 0,075 | 0,084 | 0,094 | 0,106 | 0,118 | 0,131 | 0,145 | 0,161 | 0,179 | 0,199 | 0,221 | 8,8 |
| 9,0 | 0,000 | 0,005 | 0,012 | 0,019 | 0,026 | 0,033 | 0,041 | 0,049 | 0,057 | 0,065 | 0,074 | 0,084 | 0,094 | 0,105 | 0,116 | 0,129 | 0,143 | 0,159 | 0,176 | 0,196 | 0,218 | 9,0 |
| 9,2 | 0,000 | 0,005 | 0,012 | 0,019 | 0,026 | 0,033 | 0,040 | 0,048 | 0,056 | 0,065 | 0,073 | 0,083 | 0,093 | 0,104 | 0,115 | 0,128 | 0,142 | 0,157 | 0,174 | 0,193 | 0,214 | 9,2 |
| 9,4 | 0,000 | 0,005 | 0,012 | 0,019 | 0,026 | 0,033 | 0,040 | 0,048 | 0,056 | 0,064 | 0,073 | 0,082 | 0,092 | 0,103 | 0,114 | 0,127 | 0,140 | 0,155 | 0,172 | 0,190 | 0,211 | 9,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 9,6 | 0,000 | 0,005 | 0,012 | 0,019 | 0,025 | 0,033 | 0,040 | 0,048 | 0,055 | 0,064 | 0,072 | 0,082 | 0,091 | 0,102 | 0,113 | 0,125 | 0,139 | 0,153 | 0,170 | 0,188 | 0,208 | 9,6 |
| 9,8 | 0,000 | 0,005 | 0,012 | 0,018 | 0,025 | 0,032 | 0,040 | 0,047 | 0,055 | 0,063 | 0,072 | 0,081 | 0,091 | 0,101 | 0,112 | 0,124 | 0,137 | 0,152 | 0,168 | 0,185 | 0,205 | 9,8 |
| 10,0 | 0,000 | 0,005 | 0,011 | 0,018 | 0,025 | 0,032 | 0,040 | 0,047 | 0,055 | 0,063 | 0,071 | 0,080 | 0,090 | 0,100 | 0,111 | 0,123 | 0,136 | 0,150 | 0,166 | 0,183 | 0,202 | 10,0 |
| 10,2 | 0,000 |
|
|
|
| 0,032 | 0,039 | 0,047 | 0,054 | 0,063 | 0,071 | 0,080 | 0,089 | 0,099 | 0,110 | 0,122 | 0,135 | 0,149 | 0,164 | 0,181 | 0,200 | 10,2 |
| 10,4 | 0,000 |
|
|
|
| 0,032 | 0,039 | 0,047 | 0,054 | 0,062 | 0,071 | 0,079 | 0,089 | 0,099 | 0,109 | 0,121 | 0,133 | 0,147 | 0,162 | 0,179 | 0,197 | 10,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 10,6 | 0,000 |
|
|
|
|
| 0,039 | 0,046 | 0,054 | 0,062 | 0,070 | 0,079 | 0,088 | 0,098 | 0,109 | 0,120 | 0,132 | 0,146 | 0,160 | 0,177 | 0,195 | 10,6 |
| 10,8 | 0,000 |
|
|
|
|
|
| 0,046 | 0,054 | 0,061 | 0,070 | 0,078 | 0,088 | 0,097 | 0,108 | 0,119 | 0,131 | 0,144 | 0,159 | 0,175 | 0,192 | 10,8 |
| 11,0 | 0,000 |
|
|
|
|
|
|
| 0,053 | 0,061 | 0,069 | 0,078 | 0,087 | 0,097 | 0,107 | 0,118 | 0,130 | 0,143 | 0,157 | 0,173 | 0,190 | 11,0 |
| 11,2 | 0,000 |
|
|
|
|
|
|
|
| 0,061 | 0,069 | 0,078 | 0,087 | 0,096 | 0,106 | 0,117 | 0,129 | 0,142 | 0,156 | 0,171 | 0,188 | 11,2 |
| 11,4 | 0,000 |
|
|
|
|
|
|
|
|
| 0,069 | 0,077 | 0,086 | 0,095 | 0,105 | 0,116 | 0,128 | 0,141 | 0,154 | 0,169 | 0,186 | 11,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 11,6 | 0,000 |
|
|
|
|
|
|
|
|
| 0,068 | 0,077 | 0,086 | 0,095 | 0,104 | 0,116 | 0,127 | 0,139 | 0,153 | 0,168 | 0,184 | 11,6 |
| 11,8 | 0,000 |
|
|
|
|
|
|
|
|
|
| 0,076 | 0,085 | 0,094 | 0,104 | 0,115 | 0,126 | 0,138 | 0,152 | 0,166 | 0,182 | 11,8 |
| 12,0 | 0,000 |
|
|
|
|
|
|
|
|
|
| 0,076 | 0,085 | 0,094 | 0,104 | 0,114 | 0,125 | 0,137 | 0,150 | 0,165 | 0,181 | 12,0 |
| 12,2 | 0,000 |
|
|
|
|
|
|
|
|
|
|
| 0,084 | 0,093 | 0,103 | 0,113 | 0,124 | 0,136 | 0,149 | 0,163 | 0,179 | 12,2 |
(tham khảo)
C.1 Khái quát
Đôi khi, dạng phân bố được biết trước hoặc có thể giả định hợp lý và có thể xác nhận bằng kiểm nghiệm tính phù hợp. Cách tiếp cận này để ước lượng các tham số của phân bố đó và sử dụng chúng để rút ra các đại lượng liên quan từ đó thu được ước lượng năng lực. Tỷ lệ nằm ngoài quy định có thể được ước lượng trực tiếp.
Phương pháp dùng với một số phân bố thường gặp được minh họa dưới đây.
C.2 Phân bố chuẩn
Nếu X1, …, XN là mẫu lấy từ phân bố chuẩn có trung bình µ và phương sai σ2, ước lượng của µ và σ2 là
![]()
và
![]()
Các chỉ số năng lực có thể lần lượt được ước lượng bằng công thức cho trong tiêu chuẩn này. Theo đó:
![]()
![]()
![]()
và, cuối cùng,
![]()
Tỷ lệ cá thể nằm ngoài quy định ước lượng thấp hơn L được tính là:
![]()
và tỷ lệ cá thể nằm ngoài quy định ước lượng cao hơn U được tính là:
![]()
ở đây Φ ký hiệu cho hàm phân bố của phân bố chuẩn chuẩn hóa. Tính toán thực tế của ![]() và
và ![]() có thể được thực hiện như đề cập trong 4.8.
có thể được thực hiện như đề cập trong 4.8.
C.3 Phân bố loga chuẩn
C.3.1 Khái quát
Phân bố loga chuẩn với các tham số µ và σ có hàm mật độ xác suất
![]()
trong đó X > 0 và log ký hiệu logarit tự nhiên, nghĩa là logarit cơ số e. Khi X có phân bố loga chuẩn với các tham số µ và σ thì logX có phân bố chuẩn với trung bình µ và phương sai σ2.
Nếu X1, ..., XN là mẫu lấy từ phân bố loga chuẩn, dữ liệu có thể được biến đổi thành chuẩn bằng cách lấy logarit logX1, …, logXN. Sau đó, có thể sử dụng các tính toán ở C.2. Một cách khác, có thể tính trực tiếp theo thang đo ban đầu của phép đo. Hai phương pháp này được đề cập dưới đây. Trong cả hai trường hợp, các tham số được ước lượng là:
![]()
và
![]()
C.3.2 Phân bố loga chuẩn - Biến đổi thành chuẩn
Giới hạn quy định trên và dưới phải được biến đổi để chúng trở thành logU và logL. Sau đó, có thể sử dụng các công thức ở C.2. Ví dụ, các ước lượng của Cp, ![]() và
và ![]() có thể được tính là:
có thể được tính là:
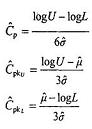
![]() và
và ![]() có thể lần lượt được đưa vào công thức thích hợp ở C.2 để tính tỷ lệ nằm ngoài quy định ước lượng.
có thể lần lượt được đưa vào công thức thích hợp ở C.2 để tính tỷ lệ nằm ngoài quy định ước lượng.
C.3.3 Phân bố loga chuẩn - Thang đo gốc
Phân vị của phân bố loga chuẩn là:
![]()
trong đó Φ-1 là nghịch đảo của hàm phân bố của phân bố chuẩn chuẩn hóa. Cụ thể:
X0,135% = e-3σ µ
X50% = eµ
X99,865% = e3σ µ
và các chỉ số ước lượng là:
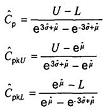
Các chỉ số này sẽ khác biệt về số so với các chỉ số thu được bằng cách tiếp cận biến đổi nêu trong C.3.2. Chủ sở hữu quá trình cùng với các cá thể phân bố loga chuẩn có thể xây dựng “cảm nhận” đối với các chỉ số, nhưng việc giải thích không nên dựa trên các điểm ngưỡng sử dụng cho chỉ số được tính với dữ liệu chuẩn.
Tính tỷ lệ cá thể nằm ngoài quy định ước lượng được tính bằng cách sử dụng các giới hạn quy định và hàm phân bố của phân bố loga chuẩn. Do đó:
![]()
và
![]()
Các ước lượng này giống hệt các ước lượng thu được bằng cách biến đổi nêu trong C.3.2.
C.4 Phân bố Rayleigh
Phân bố này hầu như chỉ sử dụng để mô tả vị trí, vấn đề lệch tâm và tràn theo hai chiều. Trong những tình huống này, thường chỉ có giới hạn quy định một phía, U.
Phân bố Rayleigh có hàm phân bố:
![]()
trong đó X > 0 và θ là tham số dương. Nếu X1, ..., XN là mẫu lấy từ phân bố Rayleigh thì tham số θ được ước lượng bởi:
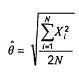
và tỷ lệ cá thể nằm ngoài quy định ước lượng được cho bởi:
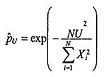
C.5 Phân bố Weibull
Đây là phân bố có tính linh hoạt cao. Phân bố này thường được sử dụng trong phân tích dữ liệu thu thập trong quá trình nghiên cứu độ tin cậy khi các dạng mô tả dữ liệu thường bất thường và không chuẩn. Phân bố này có ba tham số:
a) ξ tham số thang đo;
b) β tham số hình dạng;
c) γ tham số vị trí, thường giả định bằng 0.
Có những trường hợp khi nghiên cứu năng lực sẽ không tạo ra dữ liệu theo dạng phân bố chuẩn nhưng có thể sử dụng phân bố Weibull để mô tả dữ liệu và sau đó đưa ra cách tính thước đo năng lực hoặc hiệu năng.
Hàm phân bố của phân bố Weibull là:

và do đó phân vị của phân bố Weibull là:
Xα% = Y - ξ(-log(1-p))-β
Đặc biệt, có thể tính các phân vị X0,135%, X50% và X99,865%, kết quả là các chỉ số năng lực. Quan trọng hơn là tỷ lệ cá thể nằm ngoài quy định là
![]()
và
![]()
Tỷ lệ cá thể nằm ngoài quy định ước lượng thu được bằng cách sử dụng ước lượng của các tham số.
C.6 Phân bố nửa chuẩn
Phân bố nửa chuẩn thường được dùng để mô tả độ biến động trong đặc trưng có quy định về dung sai hình học. Trường hợp này đưa ra quy định một phía. Nó thường áp dụng khi các đặc trưng hình học, dạng và hướng được qui định.
Phân bố nửa chuẩn, với tham số µ và σ, có hàm mật độ xác suất:
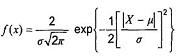
trong đó 0 ≤ X < ∞.
Phân bố nửa chuẩn tỷ lệ với phân bố chuẩn. Do đó, có thể tính tỷ lệ ước lượng của phân bố này bằng cách sử dụng bảng phân bố chuẩn chuẩn hóa với giá trị bảng thích hợp nhân với 2.
C.7 Các phân bố khác
Các phân bố được nêu ở trên là những phân bố thường gặp. Có nhiều loại phân bố khác mà người đọc có thể tìm trong rất nhiều sách về thống kê học.
(tham khảo)
D.1 Phân bố chuẩn
D.1.1 Khái quát
Điều quan trọng đối với những người tính được chỉ số năng lực là nhận thức được rằng giá trị tính được chỉ là ước lượng cho giá trị thực của chỉ số đó. Thông thường, lượng dữ liệu sử dụng để tính chỉ số càng lớn thì ước lượng sẽ càng tốt. Nội dung dưới đây nhằm báo hiệu cho người đọc thực tế này và đưa ra phương pháp tính toán khoảng tin cậy cho các chỉ số.
Các tính toán khoảng tin cậy chỉ thích hợp khi thước đo vị trí được chọn là trung bình chứ không phải trung vị.
D.1.2 Phân bố chuẩn - Phương pháp công thức
Khoảng tin cậy 1 - α là:
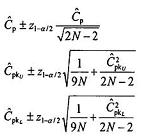
trong đó z là biến chuẩn hóa của phân bố chuẩn. Tính toán này cần được thực hiện với ít nhất 50 số đọc.
CHÚ THÍCH: Các công thức này giả định chỉ số ước lượng được tính toán bằng cách sử dụng độ lệch chuẩn dựa trên cỡ mẫu tổng (N).
D.1.3 Phân bố chuẩn - Phương pháp bảng cho chỉ số Cp
D.1.3.1 Khái quát
Ví dụ về phương pháp ước lượng khoảng tin cậy cho chỉ số Cp được trình bày ở D.1.3.2.
Phương pháp này yêu cầu tra các hệ số Kl và Ku từ Bảng D.1. Các giá trị này khác biệt tùy theo ước lượng Cp dựa trên bao nhiêu số đọc. Chỉ số được nhân với các hệ số này để cho khoảng tin cậy. Tính toán cần được thực hiện với ít nhất 50 số đọc.
Ví dụ, khoảng tin cậy 95 % sẽ là:
![]()
D.1.3.2 Qui trình và ví dụ
a) Ghi giá trị Cp ước lượng và cỡ mẫu tổng:
![]() = 1,20 và N = 100
= 1,20 và N = 100
b) Chọn mức tin cậy yêu cầu
Mức tin cậy = 95 %
c) Tra hệ số từ Bảng D.1:
![]() = 0,86
= 0,86
![]() = 1,14
= 1,14
d) Tính khoảng tin cậy
![]()
0,86 x 1,20 ≤ Cp ≤ 1,14 x 1,20
1,03 ≤ Cp ≤ 1,37
Bảng D.1 - Hệ số dùng cho khoảng tin cậy của chỉ số Cp
| Khoảng tin cậy | Hệ số |
| Cỡ mẫu tổng, N |
| ||
| 50 | 75 | 100 | 150 | 300 | ||
| 90% | Kl | 0,83 | 0,86 | 0,88 | 0,90 | 0,93 |
| Ku | 1,17 | 1,14 | 1,12 | 1,10 | 1,07 | |
| 95% | Kl | 0,80 | 0,84 | 0,86 | 0,89 | 0,92 |
| Ku | 1,20 | 1,16 | 1,14 | 1,11 | 1,08 | |
| 99% | Kl | 0,74 | 0,79 | 0,82 | 0,85 | 0,90 |
| Ku | 1,25 | 1,21 | 1,18 | 1.15 | 1,10 | |
D.2 Các khoảng tin cậy khác
Khoảng tin cậy dùng cho các chỉ số tính toán khác (không phải ước lượng bằng đồ thị) có thể thấy cho các phân bố không chuẩn cũng như cho phân bố chuẩn.
Thư mục tài liệu tham khảo
[1] TCVN 8244-1 (ISO 3534-1), Thống kê học - Từ vựng và ký hiệu - Phần 1: Thuật ngữ chung về thống kê và thuật ngữ dùng trong xác suất
[2] TCVN 8244-2 (ISO 3534-2), Thống kê học - Từ vựng và ký hiệu - Phần 2: Thống kê ứng dụng
[3] TCVN 9603 (ISO 5479), Giải thích dữ liệu thống kê - Kiểm nghiệm sai lệch so với phân bố chuẩn
[4] TCVN 9945-1 (ISO 7870-1), Biểu đồ kiểm soát - Phần 1: Hướng dẫn chung
[5] TCVN 9945-2 (ISO 7870-2), Biểu đồ kiểm soát - Phần 2: Biểu đồ kiểm soát Shewhart
[6] TCVN ISO 9000:2007 (ISO 9000:2005), Hệ thống quản lý chất lượng - Cơ sở và từ vựng
[7] ISO/IEC 12207:1995, Information technology - Software life cycle processes (Công nghệ thông tin - Các quá trình vòng đời phần mềm)
[8] AUTOMATIVE INDUSTRY ACTION GROUP. Statistical process control (SPC) - Reference material. AIAG, 2005 (Kiểm soát thống kê quá trình (SPC) - Mẫu chuẩn)
[9] CHOU Y., OWEN D.B., BORREGO S.A. Lower confidence limits on process capability indices. J. Qual. Technol. 1990, 22 (3)p.225 (Giới hạn tin cậy dưới về chỉ số năng lực quá trình)
[10] CLEMENTS, J.A. Process capability calculations for non-normal distributions. Quality Process, 22 (1989), pp. 95-100 (Tính năng lực quá trình đối với phân bố không phải phân bố chuẩn)
[11] DUNCAN A.J. Quality control and industrial statistics. Richard D.Irwin, Inc, 1986 (Kiểm soát chất lượng và thống kê công nghiệp)
[12] KOTZ, S., & JOHNSON N.L. Process Capability Indices. Chapman & Hall, 1993 (Chỉ số năng lực quá trình)
[13] KOTZ, S. and LOVELACE, C.R. Process Capability Indices in Theory and Practice. Hodder Arnold, 1998 (Chỉ số năng lực quá trình trên lý thuyết và thực hành)
[14] RODRIGUEZ R.N. Recent developments in process capability analysis. J. Qual. Technol. 1992, 24 (4) p.179 (Những phát triển gần đây trong phân tích năng lực quá trình)
[15] STEPHENS, M.A. Anderson-Darling Test for Goodness of Fit. In.: Encyclopedia of Statistical Sciences, (Johnson, N.L., & Kotz, S.eds). Wiley Interscience, Vol. 1, 1982, pp. 81-5 (Từ điển bách khoa về khoa học thống kê)
MỤC LỤC
Lời nói đầu
Lời giới thiệu
1 Phạm vi áp dụng
2 Ký hiệu và chữ viết tắt
2.1 Ký hiệu
2.2 Chữ viết tắt
3 Các khái niệm cơ bản được sử dụng cho năng lực và hiệu năng quá trình
3.1 Khái quát
3.2 Vị trí
3.3 Độ phân tán
3.4 Sai số bình phương trung bình (MSE)
3.5 Giới hạn quy chiếu
3.6 Khoảng quy chiếu (còn gọi là độ trải quá trình)
4 Năng lực
4.1 Khái quát
4.2 Năng lực quá trình
4.3 Vị trí quá trình
4.4 Chỉ số năng lực quá trình đối với dữ liệu đo được
4.5 Chỉ số năng lực quá trình đối với dữ liệu đo được (không chuẩn)
4.6 Phương pháp thay thế để mô tả và tính toán ước lượng năng lực quá trình
4.7 Thước đo năng lực khác đối với dữ liệu liên tục
4.8 Đánh giá tỷ lệ nằm ngoài quy định (phân bố chuẩn)
5 Hiệu năng
5.1 Khái quát
5.2 Chỉ số hiệu năng quá trình đối với dữ liệu đo được (phân bố chuẩn)
5.3 Chỉ số hiệu năng quá trình đối với dữ liệu đo được (phân bố không chuẩn)
5.4 Chỉ số hiệu năng khác đối với dữ liệu đo được
5.5 Đánh giá tỷ lệ nằm ngoài quy định đối với phân bố chuẩn của phân bố tổng thể
6 Báo cáo chỉ số năng lực và hiệu năng quá trình
Phụ lục A (tham khảo) Ước lượng độ lệch chuẩn
Phụ lục B (tham khảo) Ước lượng thước đo năng lực và hiệu năng sử dụng đường Pearson - Quy trình và ví dụ
Phụ lục C (tham khảo) Xác định phân bố
Phụ lục D (tham khảo) Khoảng tin cậy
Thư mục tài liệu tham khảo
- 1 Tiêu chuẩn quốc gia TCVN 11864:2017 (ISO 18404:2015) về Phương pháp định lượng trong cải tiến quá trình - Six sigma - Năng lực của nhân sự chủ chốt và tổ chức khi triển khai six sigma và lean
- 2 Tiêu chuẩn quốc gia TCVN ISO/IEC 17025:2017 (ISO/IEC 17025:2017) về Yêu cầu chung về năng lực của phòng thử nghiệm và hiệu chuẩn
- 3 Tiêu chuẩn quốc gia TCVN ISO 17034:2017 (ISO 17034:2016) về Yêu cầu chung về năng lực của nhà sản xuất mẫu chuẩn

